6.2 (I) Виды фильтров
==391
В Части _1 шло обсуждение фильтров, собранных из резисторов и конденсаторов. Такие RC секции имеют плавные характеристики изменения усиления, а спад усиления в достаточном удалении от точки «-3dB» составляет 6 dB/octave . Каскадируя ФВЧ и ФНЧ можно получить полосовой фильтр, имеющий, опять же, плавные скаты «юбки». Такие фильтры вполне подходят для многих задач, особенно если частота вырезаемого сигнала далеко отстоит от интересующей рабочей полосы. Примером могут служить радиочастотные фильтры в звуковой аппаратуре, «блокировочные» конденсаторы, убирающие постоянную составляющую или вырезающие модулирующую частоту из канальных данных.
6.2.1 АЧХ RC фильтров
Но в жизни бывают ситуации, когда требуется фильтр с более плоской характеристикой в полосе пропускания и более резким переходом к полосе заграждения. Это случается, когда полезный сигнал имеет близкую к помехе частоту. Возникает очевидный вопрос, можно ли, каскадируя несколько одинаковых секций, приблизить переходную характеристику в частотной области к идеальной «кирпичной стенке» [* т.е., к вертикальному переходу к полосе заграждения] , как на рис. 6.1 .
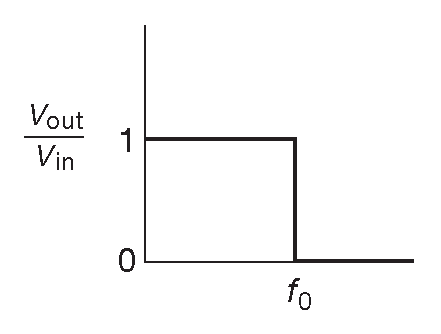
Рис. 6.1 Частотная характеристика идеального фильтра
Простое каскадирование здесь не работает, потому что входной импеданс каждой последующей секции серьёзно нагружает предыдущую, ухудшая её характеристики. Возможно, делу могла бы помочь постановка промежуточных буферов между секциями ( или реорганизация таким образом, чтобы каждый последующий каскад имел бы гораздо больший импеданс, чем предшествующий ). Но в любом случае на RC фильтрах решить задачу не получится. Их каскадирование будет увеличивать крутизну спуска , но излом на АЧХ при переходе от пропускания к заграждению ( «колено» ) острее не станет. Другими словами, из многих плавных изломов не получится сделать один резкий. Чтобы увеличить наглядность этого утверждения, были построены графики усиления ( \( V_{out}/V_{in}\) ) от частоты ( рис. 6.2 ) для ФНЧ, собранных из 1, 2, 4, 8, 16 и 32 идентичных RC секций, снабжённых промежуточными буферами.
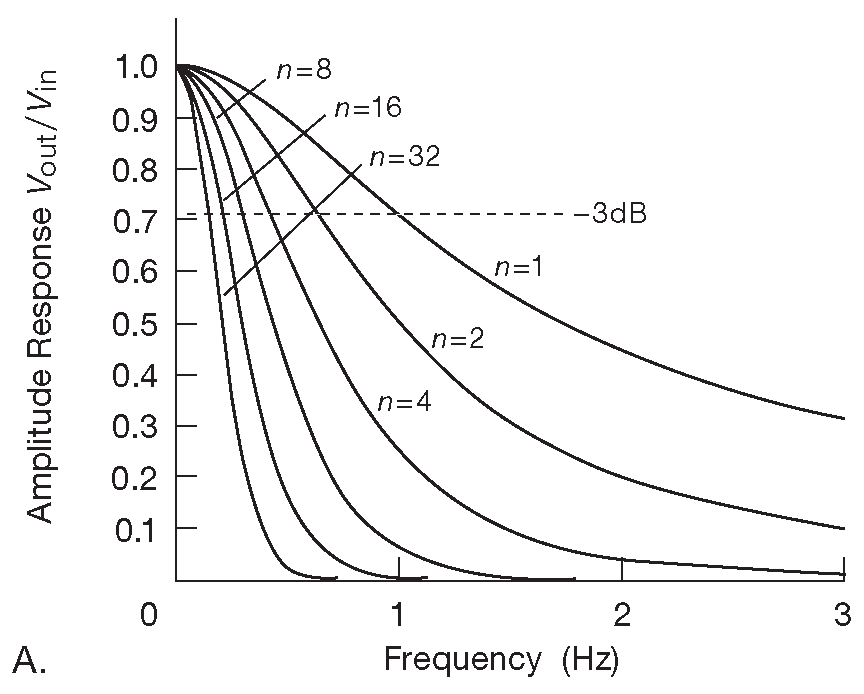
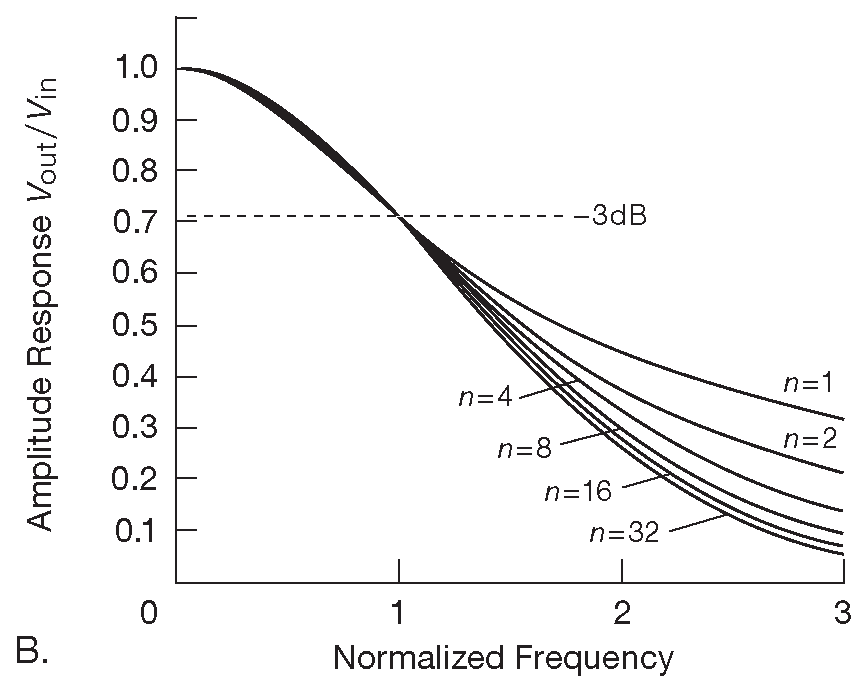
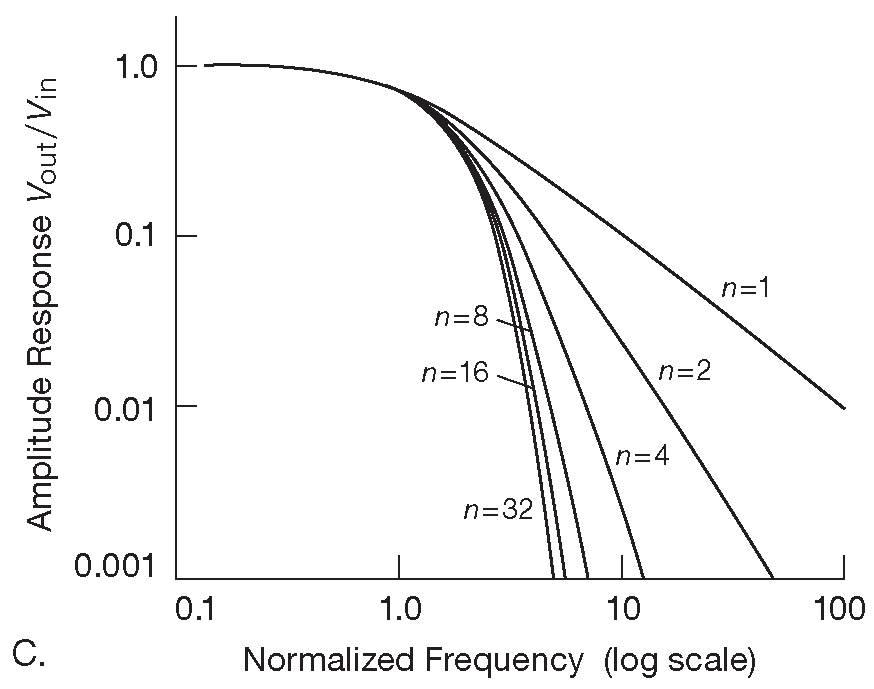
Рис. 6.2 АЧХ многосекционного RC фильтра. Графики A и B даются в линейных координатах, а C - в логарифмических. АЧХ фильтров на графиках B и C нормализована ( масштабирована ) так, чтобы точка «-3dB» находилась на единичной частоте
==392
На первом рисунке показан эффект каскадирования секций, частота \( f_{3dB} \) которых равна единице. Видно как по мере удлинения цепочки её общая частота \( f_{3dB} \) снижается, что легко предсказать и посчитать _1 . Для корректного сравнения характеристик необходимо подстраивать частоту каждой отдельной секции, чтобы их общая точка \( f_{3dB} \) не изменяла своего положения. С этой целью все остальные графики на рис. 6.2 «нормированы» по частоте так, чтобы точка «-3dB» ( или «частота среза», в зависимости от того, которая из них определена ) для всех фильтров попадала на отметку 1 ( пусть это будет 1 Hz ). Чтобы понять, как будут выглядеть графики для реальных фильтров, полученную АЧХ надо просто умножить на реальную частоту среза \( f_c\) ( или \( f_{3dB} \) ) . Кроме того, при разборе фильтров удобнее работать в лог-лог координатах, потому что так удобнее наблюдать частотный отклик. Логарифмический масштаб позволяет чётче видеть общую картину - частоту среза и величину подавления. В данном случае ( каскадированные RC секции ) нормализованные графики на рис. 6.2B,C показывают плавный перегиб характеристики.
Интересно взглянуть на фазовый сдвиг каскадированного фильтра, нормализованный опять же так, чтобы точка «-3dB» попадала на единичную частоту. Этот график приведён на рис. 6.3 . Запаздывание фазы асимптотически приближается к ( 90°×n ) для каскада длиной n , как это можно предполагать, если вспомнить плавный переход от 0° до 90° у одной RC секции ( рис. 1.104 ). Уже не столь очевидно, что сдвиг фазы в точке «-3dB» растёт одновременно с увеличением числа каскадов. Фазовая характеристика очень важна, потому что она определяет внутриполосные искажения, вносимые фильтром.
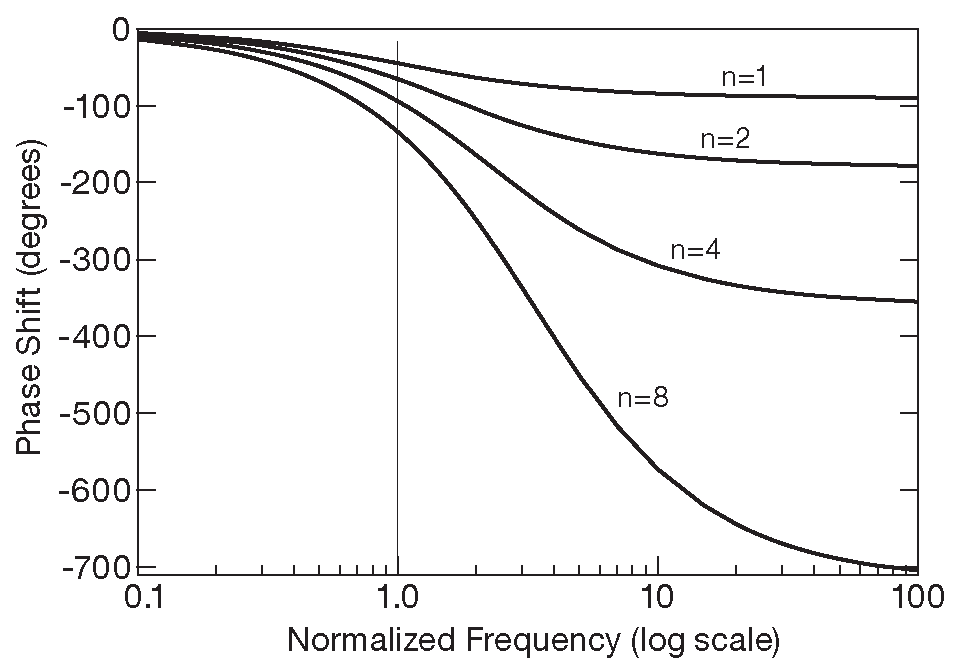
Рис. 6.3 Фазочастотные характеристики многосекционных RC фильтров, соответствующие графикам на рис. 6.2C
6.2.1.A Ухудшение общего подавления: неидеальные конденсаторы
В отличие от идеальных, реальные конденсаторы имеют несколько дополнительных «паразитных» параметров. Наиболее заметные из них - эквивалентное последовательное сопротивление ESR и эквивалентная последовательная индуктивность ESL . На очень больших частотах, где ESR становится сравнимо с реактивным сопротивлением 1/( \(ωC\) ) , реальный RC фильтр перестаёт ослаблять сигнал. Данный эффект был промоделирован в SPICE ( см. Приложение _J ) для многосекционных RC фильтров. Результат можно видеть на рис. 6.4 . Моделирование велось исходя из предположения, что надо очистить линию постоянного напряжения, питающую слаботочную схему, от высокочастотного переключательного шума, сторонних сигналов и т.п. Исходя из задачи, общий «бюджет» последовательного сопротивления составляет 100 Ω , что приемлемо для нагрузки в несколько миллиампер. Кроме того, общая ёмкость ограничена величиной 20 μF , чтобы удержать габариты узла в разумных пределах. Симуляция была проведена для трёх многокаскадных фильтров: одиночной секции 100 Ω+20 μF , двух идентичных секций 50 Ω+10 μF и четырёх секций по 25 Ω+5 μF каждая. Сначала были построены АЧХ фильтров с идеальными конденсаторами ( с ESR=0 ), а затем проведены расчёты с использованием реальных цифр ESR , взятых из справочных данных ( например, для конденсатора 5 μF×100 V это 1 Ω ).
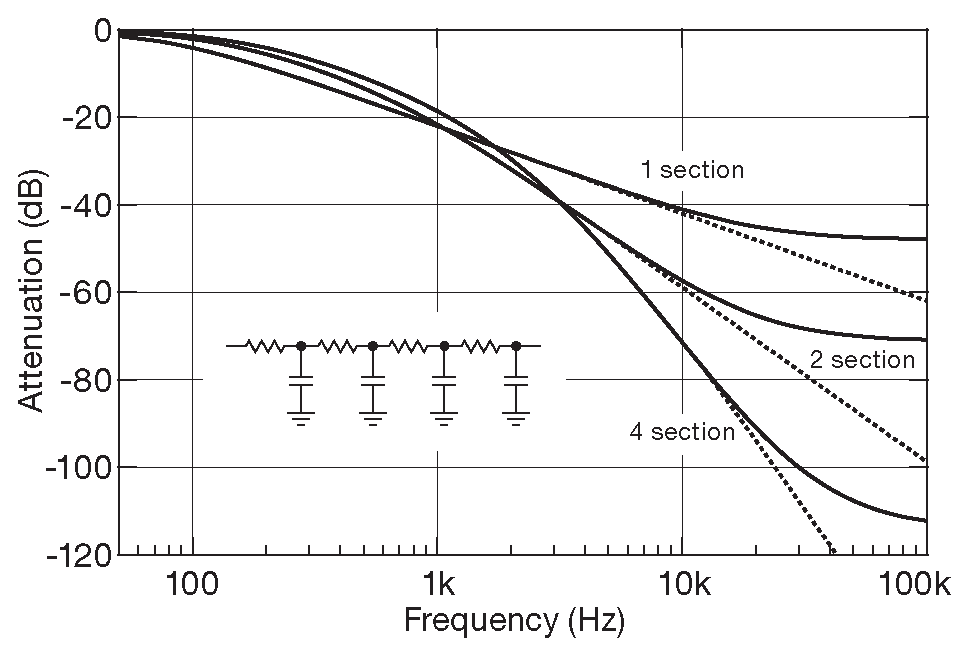
Рис. 6.4 Реальные конденсаторы имеют последовательное паразитное сопротивление, избавиться от которого нельзя. Это сопротивление ограничивает общее подавление RC фильтра. На графике приводятся идеальные ( пунктирная линия ) и реальные характеристики каскадных RC фильтров по результатам симуляции в SPICE
==393
Эффект последовательного сопротивления хорошо виден. Он проявляется в прекращении роста подавления сигналов на частотах, где импеданс конденсатора начинает приближаться к величине ESR , в то время как для идеального конденсатора график продолжает падать по закону 1/\( f \) . Кроме того, видно, что распределение ёмкости по нескольким секциям - вполне практичная идея.
6.2.2 Идеализированные характеристики LC фильтров
Фильтры, собранные из катушек индуктивности и конденсаторов могут иметь очень резкие изломы характеристики ( §1.7.14 ). Параллельная и последовательная резонансные LC цепи рассматривались в качестве примера. Драматическую разницу между RC и LC ФНЧ с одинаковыми частотами среза можно видеть на рис. 1.112 . Добавление в схему катушек индуктивности делает возможным создание фильтров с любым желаемым уровнем неравномерности АЧХ в полосе пропускания в сочетании с резкостью перехода и уровнем подавления в полосе заграждения. На рис. 6.5 приведена схема телефонного фильтра и его впечатляющая полосовая характеристика _2 .
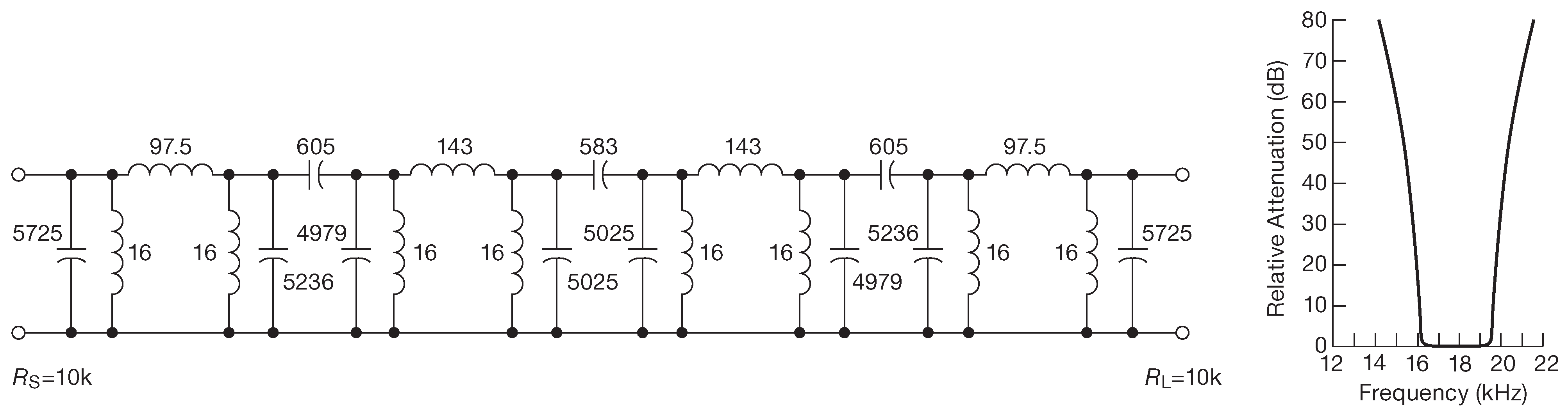
Рис. 6.5 Слева: неожиданно хороший полосовой пропускающий фильтр ( индуктивности в mH , ёмкости в pF ). Справа: измеренная характеристика фильтра. Великолепная чёткость срезов по границам полосы пропускания смазывается очень плохой фазовой характеристикой, см. §6.2.5 . Уровень 0 dB соответствует ∼9 dB потерь и импедансам источника и нагрузки по 10 kΩ у каждого
Очевидно, что привнесение в схему индуктивностей добавляет чего-то, чего невозможно достичь иными методами. В терминах теории цепей это «что-то» является «полюсами, не лежащими на осях» ( см. Часть X1 [* ##§X1.5 ] ). Но даже с индуктивностями сложность фильтра увеличивается в соответствии с требуемой гладкостью АЧХ в полосе пропускания и резкостью перехода к заграждению вне её, а от сложности зависит число компонентов. Кроме того, по мере приближения АЧХ к форме вертикальной стенки, всё хуже начинает выглядеть переходная и фазочастотная характеристика.
6.2.3 Несколько простых примеров
Пугающе сложный фильтр Орчада-Шихана на рис. 6.5 показывает, чего можно достичь с помощью синтеза классических LC фильтров _3 . Но чтобы создавать хорошие _4 конфигурации, которые будут решать поставленные задачи, вовсе не обязательно становиться непревзойдённым специалистом по проектированию фильтров. Ниже приводятся три примера простых фильтров, созданных авторами по заказу родной радиообсерватории.
==394
6.2.3.A Синусоидальный сигнал из меандра
Цифровая электроника позволяет легко создавать и преобразовывать импульсные последовательности и сигналы с точно заданными частотами, но в обсерватории, где работают авторы, требуется только синусоидальное напряжение. На рис. 6.6 показан один из путей получения синусоидального сигнала из прямоугольного с постоянной частотой - настроенный последовательный LC фильтр. Он выглядит, как очень маленький импеданс на частоте резонанса ( \( f_0=1/( 2π\sqrt{LC})\) ) _5 , а по мере удаления от неё импеданс асимптотически растёт \(∝\) 1/\( f \) на низких частотах и \(∝ f\) на высоких. [* См. также рис. X9.61 на стр. X_435 ] .
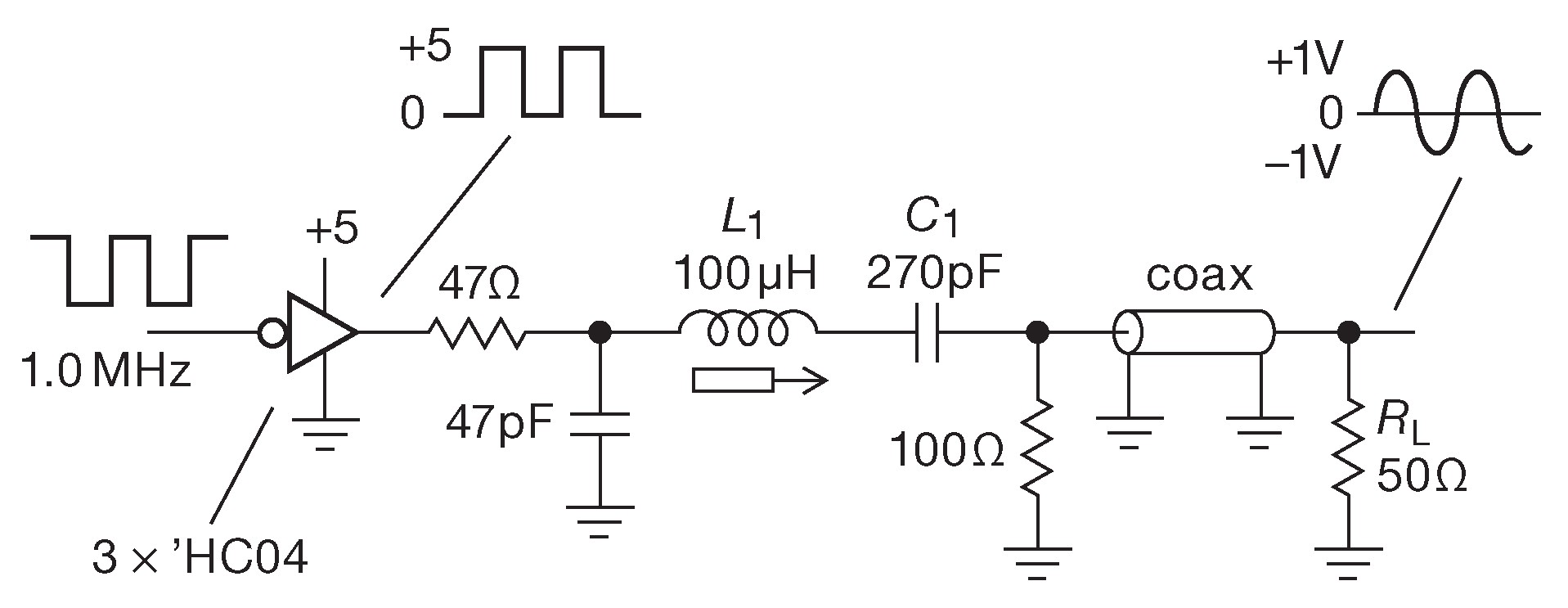
Рис. 6.6 Последовательный полосовой пропускающий LC фильтр превращает меандр в синусоидальный сигнал на 50-омной нагрузке
Номиналы LC подобраны под частоту 1 MHz таким образом, чтобы реактивное сопротивление \(X_L\) на частоте 3 MHz ( в прямоугольном сигнале имеются только нечётные гармоники, и это первая из них ) было велико по сравнению с 50-омной нагрузкой. Для \(L_1\)=100 μH импеданс на частоте 3 MHz составляет \(X_L\)=2\(πfL\)≈2 kΩ .
На рис. 6.7 показаны результаты работы реальной схемы. Некоторый прогиб прямоугольного сигнала возникает из-за нагрузки в виде фильтра и 50-омного приёмника. RC цепочка на входе LC фильтра увеличивает время нарастания, чтобы резкие фронты прямоугольного сигнала не лезли на выход через паразитную ёмкость катушки индуктивности и не портили выходной синус небольшими засечками. Обозначение «3×’HC04» указывает использованное семейство логических микросхем, см. Часть 10 .
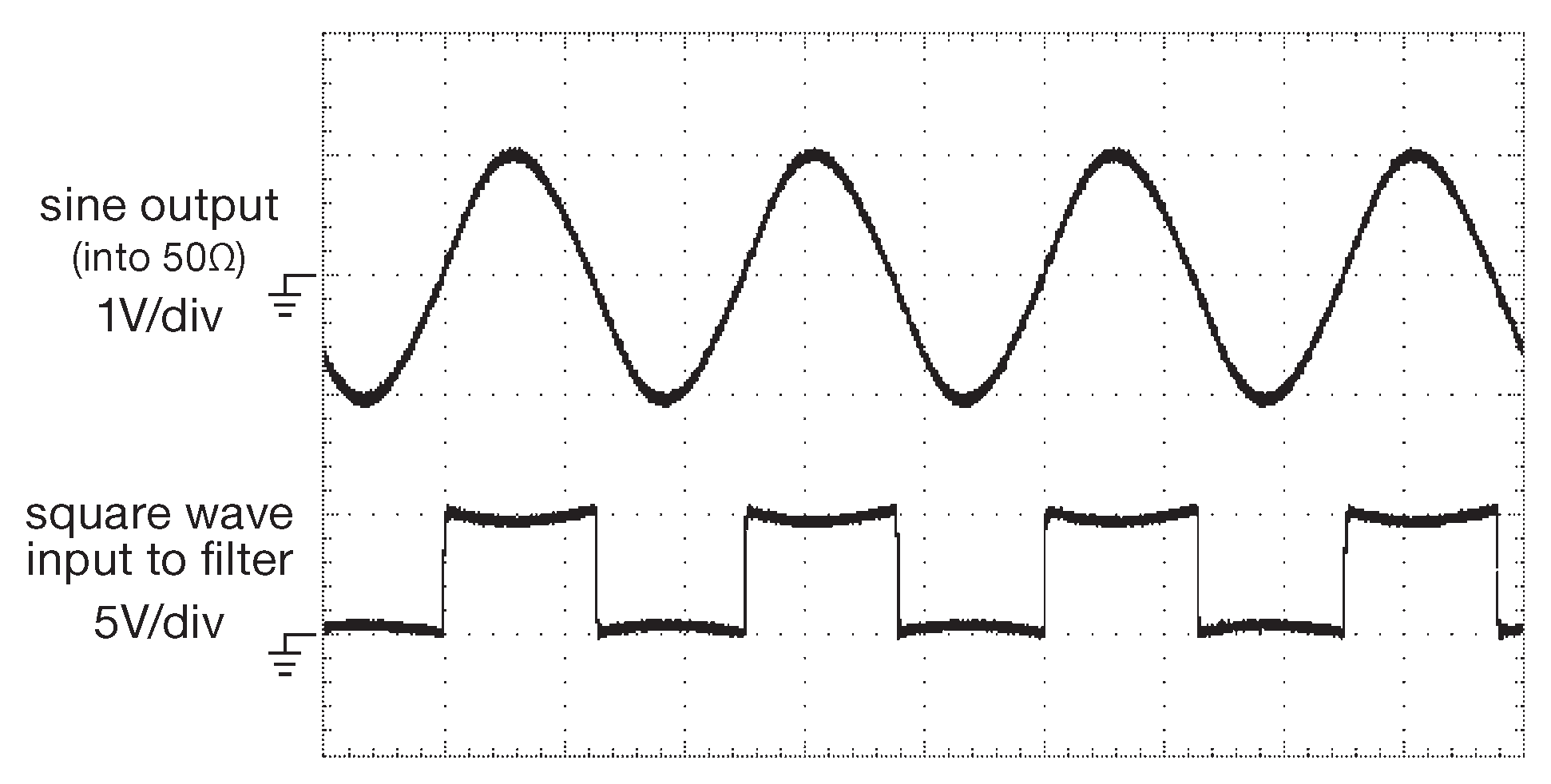
Рис. 6.7 Вход ( нижний луч ) и выход последовательного полосового LC фильтра по схеме 6.6 , нагруженного на 50 Ω . По горизонтали 400 ns/div , по вертикали 1 V/div ( верхний луч ) и 5 V/div ( нижний ) [* см. §A.4* ]
6.2.3.B Удаление интерференционных пиков
Красивая техника, именуемая «синтез частоты с использованием фазовой автоподстройки» ( см. §13.13.6.A и §13.13.6.B ), позволяет получить сигнал любой частоты с высокой точностью её установки из единственной исходной, например, 10 MHz . На рис. 6.8 показана блок-схема синтезатора на 78 MHz с использованием PLL . Основная идея - использование генератора управляемого напряжением ( VCO ) и сравнение частоты на его выходе с опорной частотой. Для удобства сравнения любая из частот или обе вместе мугут быть поделены с любым целым коэффициентом. Разница частот создаёт сигнал ошибки, с помощью которого подстраивается частота VCO. В предложенной схеме опорная частота делится на 50 ( т.е. получается 200 kHz ), и сравнивается с выходом VCO, поделенным на 390 . Чтобы получить после такого делителя те же 200 kHz , на вход надо подать 78 MHz .
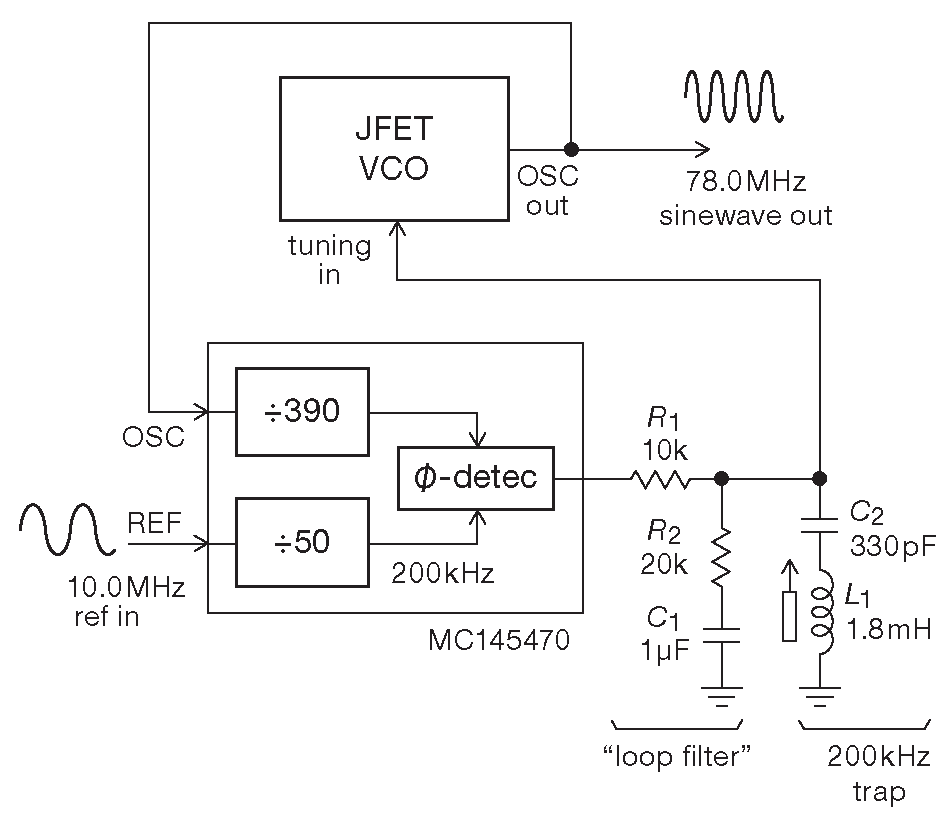
Рис. 6.8 Последовательные RC и LC цепи подавляют интерференционные компоненты от частоты 200 kHz на выходе VCO в схеме фазовой автоподстройки частоты
==395
Был собран простой, но вполне рабочий генератор на полевом транзисторе ( рис. 7.29 ), почти вся выходная энергия которого концентрировалась на основной частоте. Некоторая доля выходной мощности попадала в нежелательную область спектра, отстоящую от основной частоты на ±200 kHz . Для её подавления поперёк управляющего выхода была добавлена простая LC цепочка, настроенная на 200 kHz . Остальные компоненты схемы ( \(R_1\) , \(R_2\) и \( C_1 \) ) образуют классический петлевой фильтр цепи фазовой автоподстройки ( см. §13.13 ).
6.2.3.C Спектральный фильтр нижних частот
Аналоговые сигналы можно оцифровывать, периодически замеряя их амплитуду и переводя результат в цифровую форму. Данный процесс сопровождается резными побочными эффектами ( рис. 13.60 ) как от конечной точности измерения амплитуды, так и ненулевого времени между соседними измерениями. Правильным выбором глубины оцифровки ( точности ) и частоты измерения ( выборки ) эффекты можно снижать до некоторого уровня.
Но в данном случае важнее тот факт, что измеряемый сигнал не должен иметь в своём составе гармоники, превышающие половину частоты измерения ( \( f_s\) ) . Данное ограничение носит название критерий Найквиста _6 . Проще всего обеспечить его выполнение, пропустив сигнал через спектральный ФНЧ, давящий гармоники высшего порядка. Частота среза такого фильтра должна обеспечивать гарантированное подавление частотных компонент выше предела Найквиста \( f_s\)/2 . Здесь обычно требуется фильтр с резким переходом к полосе заграждения, в противном случае придётся поднимать частоту \( f_s\) , чтобы не допустить пролезание высших гармоник под плавный срез. Кроме того, желательно иметь плоскую АЧХ в полосе пропускания.
В приёмнике сигнала с радиотелескопа ( рис. 6.9 ) используется умножитель , чтобы преобразовать сигналы в полосе шириной 2 MHz с центром на частоте 78 MHz в сигналы в полосе 2 MHz с центром в 0 Hz . ( 78 MHz здесь – «промежуточная частота» ( IF ), а 0 Hz – «базовая» ). Умножитель создаёт две синусоиды - сумму и разность входных частот: \(\cos(ω_1t )\cos(ω_2t ) \)= \(^{1}/_{2}\left[{\cos(ω_1 - ω_2 )t + \cos(ω_1+ω_2 )t}\right]\) . На входе умножителя сигнал с телескопа и фиксированная частота 78 MHz ( называемая «местный генератор» - LO ), на выходе - сигнал в базовой полосе от 0 Hz до 1 MHz _7 , который требуется оцифровать и исследовать _8 .
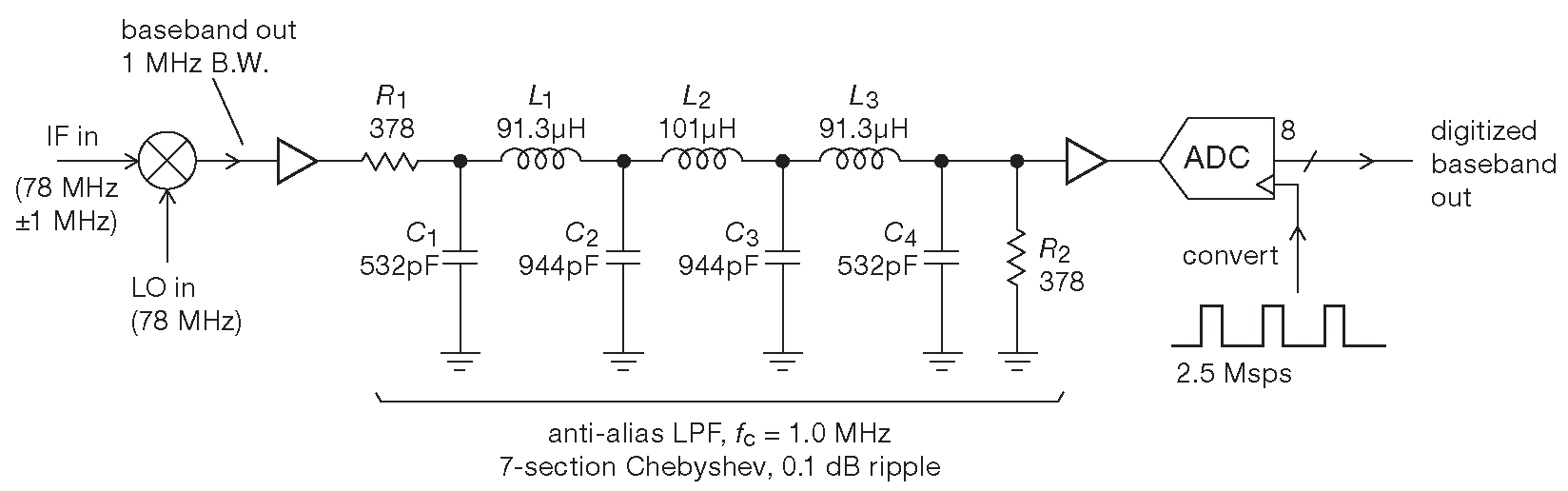
Рис. 6.9 7-звенный LC ФНЧ с резким срезом не допускает проникание нежелательных компонентов спектра из приемника для радиотелескопа, отсекая частоты выше границы Найквиста ( 1.25 MHz или \({f_c}\)/2 ). Для обсерватории были построены 126 таких фильтров, см. фотографию 1.111
Далее сигнал в базовой полосе усиливается и прогоняется через серьёзный спектральный фильтр, а именно: 7-звенный LC ФНЧ Чебышева с частотой среза 1.0 MHz и неравномерностью по амплитуде 0.1 dB _9 . Фильтр проектировался под несколько необычное значение входного и выходного импеданса ( 378 Ω ), чтобы воспользоваться возможностями стандартных подстраиваемых катушек индуктивности. Он убирает все спектральные компоненты выше 1 MHz , а вычищенная базовая полоса вновь усиливается, а затем оцифровывается ( с помощью устройства, называемого «аналогово-цифровой преобразователь» ) со скоростью 2.5 Msps . Соответствующая частота Найквиста равна 1.25 MHz и попадает прямо в полосу заграждения ФНЧ с очень крутым срезом. Фактические параметры оказались очень близки к расчётным: на частоте Найквиста входной сигнал ослабляется на 20 dB , а на частоте 1.5 MHz , где группируются наиболее вредные компоненты спектра, давится ещё на 16 dB . Это замечательные параметры для легко рассчитываемой и собираемой схемы, особенно если сравнивать их с результатами для RC аналога с таким же числом компонентов, в котором на частоте 1.25 \( f_с\) ослабление относительно сигнала \( f_c\) составляет всего 1.6 dB . В графическом виде картина представлена на рис. 6.10 и 6.11 .
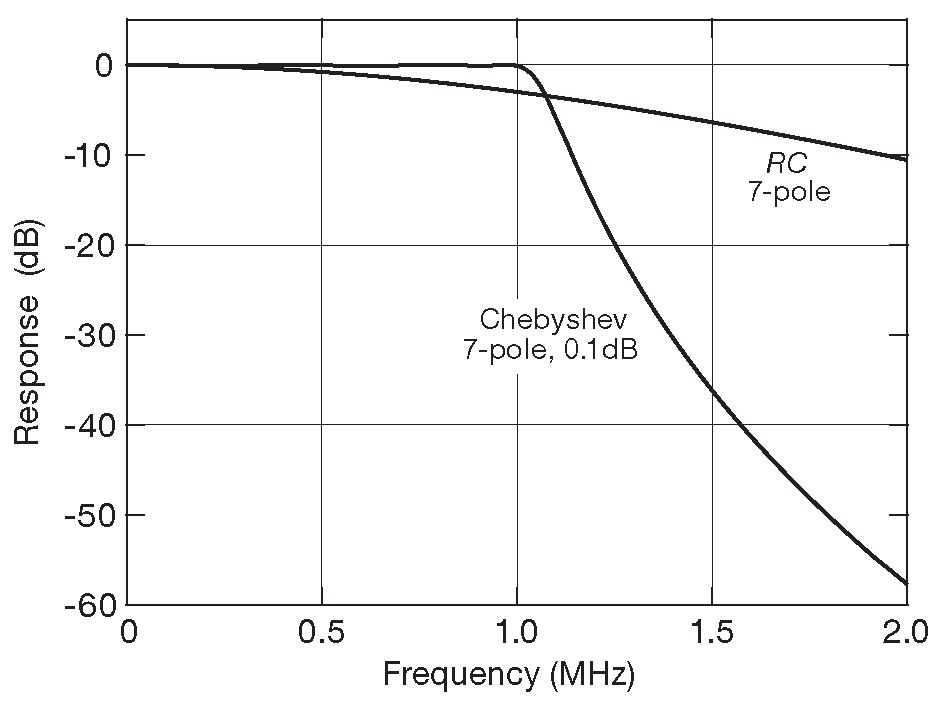
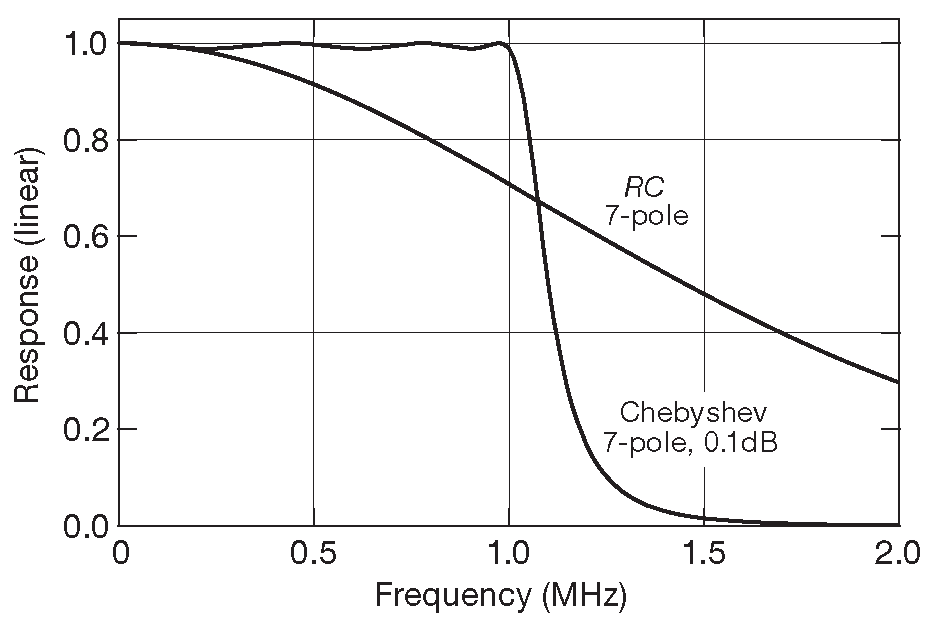
Рис. 6.10 Резкий срез 7-звенного LC фильтра с рис. 6.9 в сравнении с плавным перегибом 7-секционного RC фильтра с такой же частотой среза ( 1 MHz ) [* см. также 1.112 ]
Рис. 6.11 Та же пара фильтров, что и на рис. 6.10 , но теперь в линейных координатах. Неравномерность фильтра Чебышева в полосе пропускания ( +0 dB/—0.1 dB или ±0.6% по амплитуде ) в таком формате видна лучше, зато неразличимы подробности подавления в полосе заграждения
==396
6.2.3.D Пассивные дифференциальные фильтры
Большинство скоростных АЦП имеют дифференциальные входы, см. §13.6.2 , а многие к тому же требуют низкоомного источника сигнала и шунтирующего конденсатора. Усилители с низкоимпедансным высокочастотным выходом рассматриваются в §5.17 , где, в том числе, на рис. 5.102 показан собранный по рекомендациям в справочных данных на AD9225 ( 25 Msps АЦП, см. также рис. 13.28 ) дифференциальный ФНЧ, состоящий из двух 50-омных резисторов и конденсатора 100 pF . Спектральные фильтры для дифференциальных входов АЦП требуются достаточно часто. Как раз для таких случаев у Texas Instruments есть отличная заметка о преобразовании однополярных фильтров в дифференциальные ##SLWA053B ( «Конструировании дифференциальных фильтров для быстрых сигналов» ).
6.2.4 Активные фильтры: общий обзор
Синтез фильтров из пассивных компонентов R, L и C - очень хорошо изученная область с массой литературы ( например, авторитетная работа Зверева [61] , см. Приложение _N ). В настоящий момент появились отличные программные средства, которые превращают расчёт конструкции в рутинную деятельность. Но индуктивности как схемные элементы оставляют желать лучшего. Часто они громоздки, дороги и слишком далеко отклоняются от идеальной модели. Потери и патологии в них слишком велики: высокое последовательное сопротивление, нелинейность, распределённая ёмкость обмоток, чувствительность к магнитным наводкам. Более того, индуктивность, нужная для низкочастотных фильтров, может потребовать физических элементов с устрашающими габаритами. И, наконец, фильтры на физических емкостях и индуктивностях нельзя перестраивать электрическим сигналом.
==397
Требуется метод построения фильтров без индуктивностей, обладающих при этом параметрами классических RLC фильтров. В идеале должна присутствовать подстройка или постоянным уровнем, или изменением частоты управляющего сигнала.
Операционные усилители позволяют строить схемы с параметрами RLC фильтров, но без физических катушек индуктивности. Такие конструкции называют активными фильтрами из-за наличия активного элемента - усилителя. Будет рассмотрен и другой класс фильтров - схемы на переключаемом конденсаторе [* или фильтры «дискретного времени» ] . В них переменные резисторы заменены МОП ключами. Характеристики таких фильтров аналогичны параметрам обычных активных фильтров ( которые иногда называют фильтрами «непрерывного времени» ), но, кроме того, позволяют изменением частоты тактирования точно настраивать частоту среза в широких пределах. Платить за подстройку приходится появлением дополнительного шума переключения и уменьшением динамического диапазона, см. §6.3.6 .
Активные фильтры можно использовать в качестве ФНЧ, ФВЧ, полосовых пропускающих и полосовых заграждающих. Плюс можно подбирать частотные характеристики: максимальную неравномерность в полосе пропускания, резкость перехода к заграждению и равномерность задержки от частоты ( об этом ниже ). Кроме того, можно создавать как «всепропускающие» фильтры - с плоской АЧХ, но заданной зависимостью фазы от частоты ( их ещё называют «корректорами задержки» ), так и их противоположность - с постоянным сдвигом фазы, но заданной АЧХ.
6.2.4.A Преобразователь отрицательного сопротивления, гиратор и обобщённый преобразователь импеданса
Существуют три интересных схемных элемента, которые требуют рассмотрения в теме активных фильтров: преобразователь отрицательного сопротивления ( NIC ), гиратор и обобщённый преобразователь импеданса ( GIC ) 10 . Эти элементы могут имитировать параметры индуктивностей, используя в дополнение к ОУ только резисторы и конденсаторы.
После разбора принципов работы означенных схем станет возможно построение RLC фильтров с идеализированными параметрами и без физических катушек индуктивности, т.е. откроется первый путь построения активных фильтров.
6.2.4.B Преобразователь отрицательного сопротивления
Преобразователь отрицательного импеданса - NIC превращает импеданс в его отрицательный эквивалент [* (–1)×n ] , а гиратор превращает импеданс в обратную величину [* 1/n ] . Следующее упражнение поможет разобраться, как это работает. [* См. также §X2.12 ]
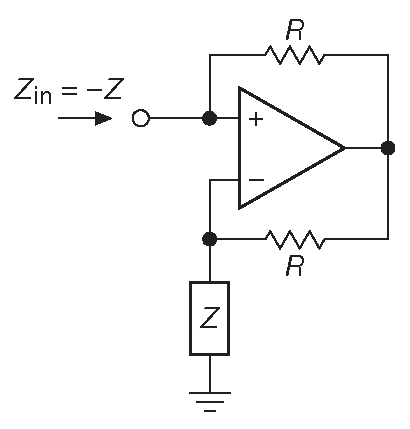
Рис. 6.12 Преобразователь отрицательного сопротивления
Упражнение 6.1
Покажите, что устройство на рис. 6.12 является преобразователем отрицательного сопротивления, т.е., что \(Z_{in}=-Z\) .
Подсказка: подайте на схему напряжение \( V_{in}\) , подсчитайте входной ток \(I\) , а затем найдите отношение \(Z_{in}=V/I\) .
NIC преобразует конденсатор в «обратную» индуктивность: \[ Z_C=\frac{1}{jωC} \to Z_{in}=\frac{j}{ωC} \quad, \qquad [6.1] \] т.е. она проявляет признаки индуктивности ( создаёт ток, задержанный по отношению к приложенному напряжению ), но имеет при этом неправильную зависимость от частоты ( снижается с увеличение частоты вместо увеличения ).
6.2.4.C Гиратор
С другой стороны, гиратор преобразует конденсатор в правильную индуктивность: \[ Z_C=\frac{1}{jωC} \to Z_{in}=jωCR^2 \quad, \qquad [6.2] \] т.е. в индуктивность с номиналом \(L=CR^2\) .
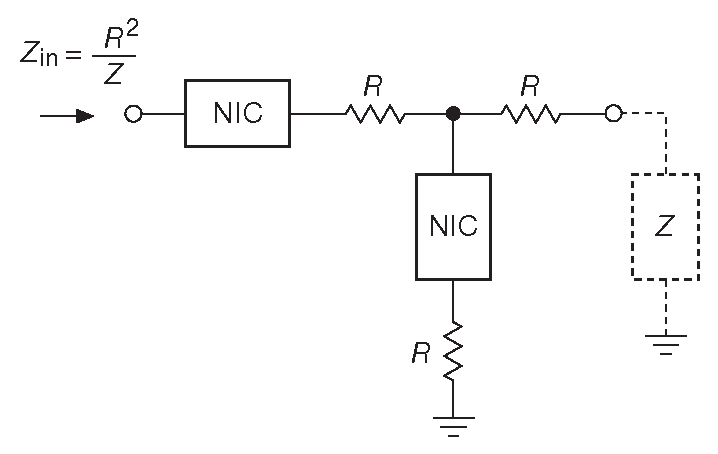
Рис. 6.13 Реализация гиратора на преобразователях отрицательного импеданса
==398
Сам факт существования гиратора приводит к пониманию принципиальной возможности построения любого фильтра только с помощью гираторов и конденсаторов без использования физических катушек индуктивности 11 . Это очень правильное использование столь необычного схемного элемента. Показанный ранее телефонный фильтр в виде забора из множества LC секций, собран на самом деле на гираторах ( по схеме гиратора Риордана, который отличается от схемы на рис. 6.13 ). Но кроме простой замены индуктивностей гираторами в существующих RLC цепях становится возможен синтез иных топологий фильтров.
Упражнение 6.2
Покажите, что схема 6.13 является гиратором, т.е. \(Z_{in}=R^2/Z\) .
Подсказка: схему можно рассматривать как набор делителей напряжения и начать её разбор справа [* подобно разбору R-2R цепочки ## ] .
6.2.4.D Обобщённый преобразователь импеданса
Схема 6.14 известна под именем «обобщённый преобразователь импеданса» ( GIC ) 12 . Она умножает импеданс \(Z_5\) на отношение ( \(Z_1Z_3 )/(Z_2Z_4\) ) . Если в качестве \(Z_4\) взять конденсатор, а во все остальные места поставить резисторы, то получится индуктивность с номиналом \(L=( R_1R_3R_5/R_2 )C_4\) , т.е. схема превратится в гиратор. Но GIC способен на большее. Например, если поставить конденсаторы вместо \(Z_3\) и \(Z_5\) , то получится частотно зависимый отрицательный резистор ( FDNR ). Фильтры на подобных элементах очень популярны в звуковой технике, т.к. считается, что они превосходят фильтры Саллена-Ки ( см. §6.2.4.E ) по шумовым характеристикам и уровню искажений. Область безындуктивных фильтров цветёт и пополняется новыми топологиями едва ли не каждый месяц.
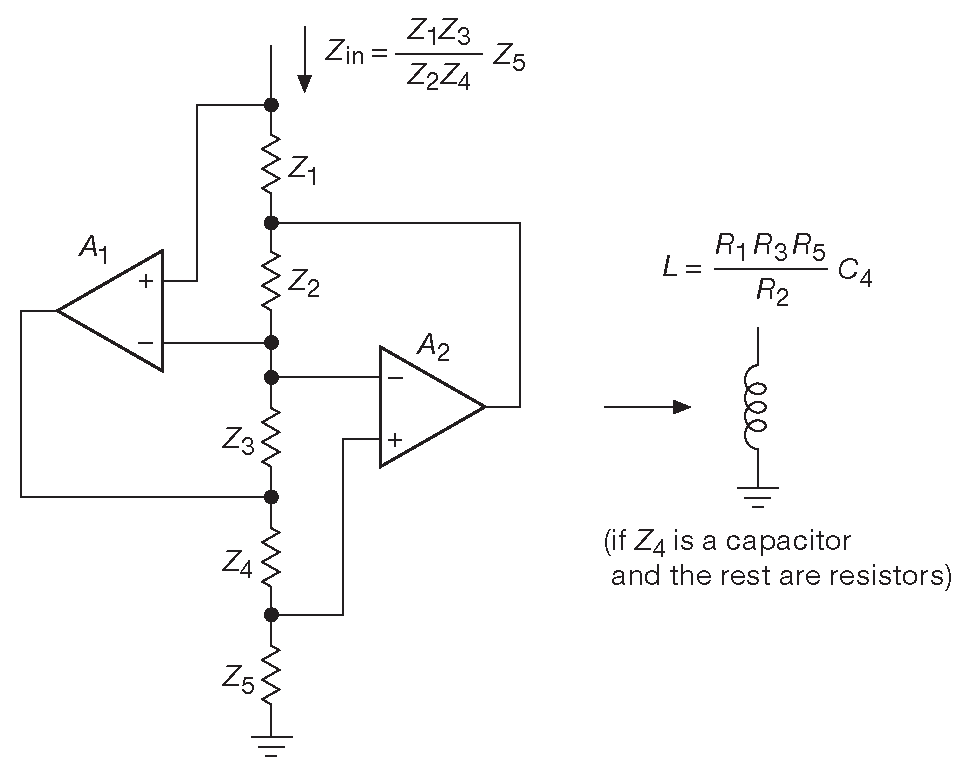
Рис. 6.14 Обобщённый преобразователь импеданса. Если в качестве \(Z_4\) взять конденсатор, а для остальных импедансов - резисторы, то схема будет вести себя подобно индуктивности. По A. Antoniou, lEE Proc., 116, 1838-1850 ( 1969 )
Ограничения
Как и в случае всех прочих схем на ОУ, гираторы, NIC и GIC сильно зависят от рабочей полосы усилителя ( и других параметров ). Таким образом, индуктивность, выполненная на GIC ( конденсатор на месте \(Z_4\) , резисторы - всё остальное ) перестаёт работать уже на частотах, превышающих несколько процентов от рабочей полосы ОУ ( \( f_T \) ) . Результаты моделирования ( рис. 6.15 ) показывают, что получится в итоге. Грубо говоря, практически идеальная на низких частотах индуктивность начинает вести себя на высоких как конденсатор, а границей между этими двумя режимами является частота резонанса 13 . Ситуация, без сомнения, огорчительная, но здесь стоит заметить, что на низких частотах такая «индуктивность» будет иметь очень высокую добротность \(Q\) - на уровне \( 2×10\space^5\) на частоте 1 kHz . Здесь предполагается, что нижняя граница импеданса, т.е. потери в индуктивности, определяется только эквивалентным последовательным сопротивлением ESR=4.8 mΩ , но в реальной жизни у катушки есть и другие потери, поэтому добротность, превышающая величину Q=1000 , для индуктивности в доли генри - очень, очень неплохой результат. Входная ёмкость скоростных ОУ ( \( f_T \)=50 MHz ) составляет всего 2.3 pF . Получить такие же низкие значения «ёмкости обмоток» или столь высокую частоту собственного резонанса в индуктивности величиной 160 mH невозможно.
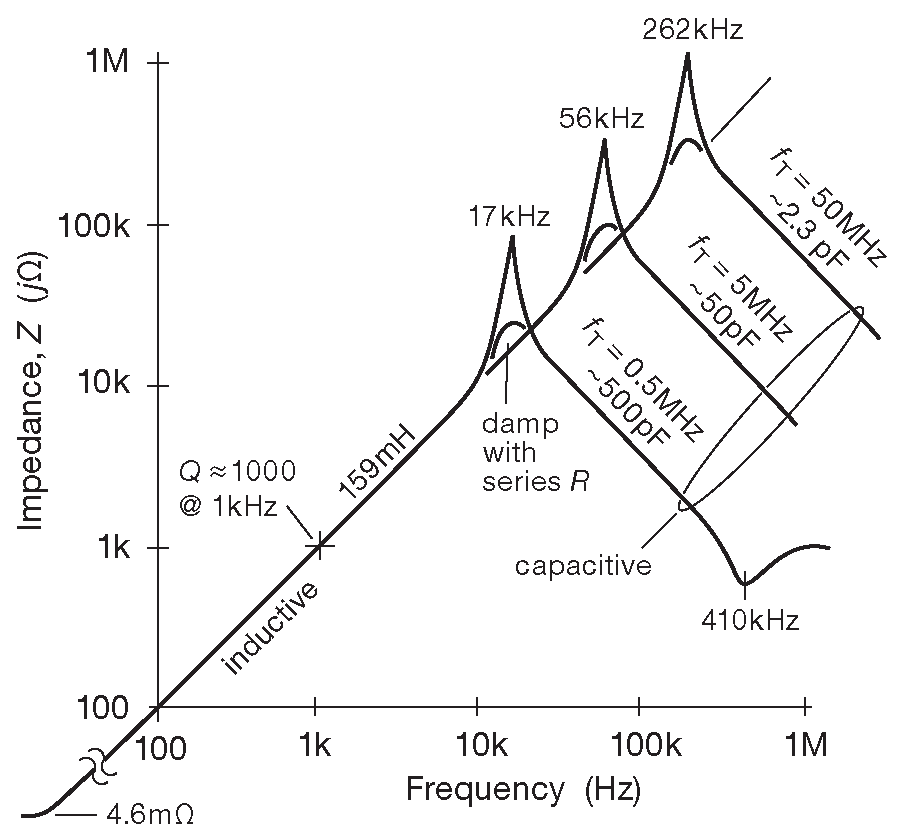
Рис. 6.15 Результаты моделирования в SPICE. Конечная рабочая полоса ОУ ухудшает идеальную GIC индуктивность и превращает её в ёмкость, уже начиная с частот, составляющих малую часть от \( f_T \) . Но даже в этом случае сравнение с физической катушкой индуктивности, обладающей ёмкостью обмотки и частотой собственного резонанса, показывает однозначное преимущество GIC индуктивности с теми же параметрами. У последней «ёмкость обмоток» и «частота резонанса» определяются рабочей полосой ОУ. ( Следует иметь в виду, что для построения графиков использовались идеальные конденсаторы )
Гираторы вполне себе используются в реальных фильтрах, см. заметку по применению, в которой Texas Instruments предлагает использовать многокаскадные GIC для построения спектральных фильтров 14 . Stanford Research Systems использует четыре GIC, из которых собран R+LC делитель, являющийся основой эллиптического фильтра низких частот ( 8 нулей, 9 полюсов ) для SR830 - синхронного усилителя на базе DSP. «Таким образом, все частотные компоненты, превышающие половину частоты выборки, подавляются как минимум на 96 dB». Скорость работы АЦП составляет 256 kHz , а фильтр пропускает частоты от постоянного тока до 102 kHz . Дополнительный запас 25% по частоте используется для достижения заявленных 96 dB подавления 15 . Полная схема фильтра включена в замечательно информативную документацию к прибору - фирменный знак всей продукции фирмы SRS.
==399
6.2.4.E Фильтр Салена-Ки
На рис. 6.16 показаны примеры простых и даже довольно понятных фильтров, построенных по уже знакомой из §4.3.6 топологии. Эти схемы названы по именам первооткрывателей фильтрами Саллена-Ки ( Sallen-and-Key ) 16 . В качестве буфера может использоваться включённый повторителем ОУ или обычный эмиттерный ( или истоковый ) повторитель. На схема показаны 2-полюсные ФНЧ и ФВЧ. Разберём в качестве примера ФНЧ ( рис. 6.16A ). Если не учитывать вольтодобавку с выхода, которая подпирает нижний конец первого конденсатора, перед нами простой двухкаскадный RC фильтр. Легко показать, что на высоких частотах схема будет иметь такой же наклон характеристики, как и две последовательные RC цепочки, потому что на выходе в этот момент будет нуль. По мере уменьшения частоты сигнал на выходе увеличивается, а вольтодобавка стремится снизить воздействие первой секции, заостряя перегиб на АЧХ. Вся эта жестикуляция не может, конечно, заменить точный анализ, который, к счастью, уже сделан для умопомрачительного числа отличных фильтров. После некоторого пояснения типов фильтров и их параметров данная схема будет вновь рассмотрена в §6.3 .
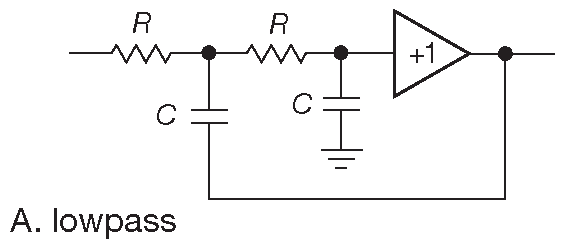
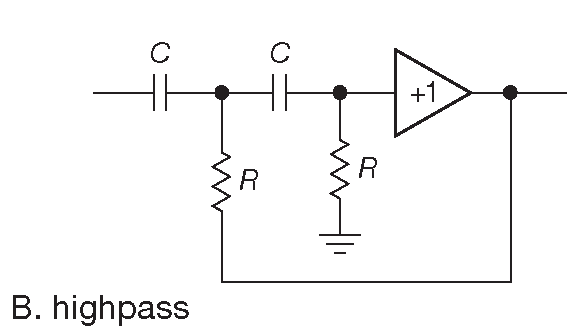
Рис. 6.16 Фильтры низких и высоких частот Саллена-Ки. На общие параметры этих простых схем влияет ненулевой выходной импеданс повторителя, см. рис. 6.36
==399
1 Этот обратный сдвиг частоты среза иногда называют «коэффициентом сжатия» . Для n идентичных последовательных буферированных RC ФНЧ частота «3dB» считается как \( f_{3dB}(n )/f_{3dB}(1)=\sqrt{2^{[1/n]}-1}\) . <-
2 Зато не показана не столь впечатляющая фазовая характеристика в полосе пропускания: 495° запаздывания на частоте 16.5 kHz . Нелинейность увеличивается ( правильнее было бы говорить «закручивается» ) до 1270° на 19.5 kHz . К счастью, фаза мало виляет на восприятие звука. <-
3 Схема опирается на рис. 11 и 12 из статьи Orchard, H. J., and Sheahan, D. E., “Inductorless Bandpass Filters”, IEEE Journal of Solid-State Circuits, Vol. SC-5, No. 3 ( 1970 ), где разработчики показывают реализацию активного фильтра, подменяющего собой эту сложную конструкцию из пассивных компонентов. Основная мысль публикации состоит в том, что схему с более высокими параметрами и в меньших габаритах можно создать, если заменить физические катушки индуктивности гираторами ( §6.2.4.C ). Схема из статьи была выполнена с использованием «гираторов Риордана», в которых каждая индуктивная π-секция ( три катушки, включая одну плавающую ) была выполнена на счетверённом ОУ, девяти резисторах и двух конденсаторах. Орчад и Шихан утверждают, что для получающихся «индуктивностей» вполне достижима добротность более 1000 , а основные сложности доставляет величина произведения усиление-полоса [* т.е. GBW ] доступных ОУ. Используемая ими техника реализации гиратора из ранних 1970-х занимает 1 кубический дюйм и имеет значительно более высокие параметры, нежели цифры, достижимые с помощью обычных индуктивностей. Заинтересовавшиеся читатели могут обратиться к статье R. H. S. Riordan, “Simulated inductors using differential amplifiers,” Electronic. Letters 3, pp. 50-51 ( Feb. 1967 ). <-
4 «Лучшее - враг хорошего». Высказывание приписывается советскому адмиралу Сергею Горшковы, Карлу фон Клаузевицу и Вольтеру. (“..Soviet Admiral Sergei Gorshkov, to Carl von Clausewitz, and to Voltaire.”) <-
5 Если бы потерь в индуктивности и конденсаторе не было, импеданс был бы равен нулю. <-
6 Нарушение данного правила приводит к возникновению фантомных сигналов , т.е. появлению в выходном цифровом потоке сигналов, изначально отсутствовавших в измеряемом напряжении, см. §13.5.1.B ). <-
7 И сигнал с частотой 156 MHz , который вырезается спектральным ФНЧ. <-
8 Дальше сигнал проходит преобразование Фурье и распадается на спектральные составляющие. Если точно, то в базовой полосе присутствуют сигналы от -1 MHz до +1 MHz , которые одиночный умножитель ужимает в одну полосу 0...1 MHz . Чтобы получить полную полосу сигнала, используются два умножителя: один для синусоидального LO сигнала, а другой - для косинусоидального. Сигналы в паре имеют имена «I» и «Q» . Оба независимо оцифровываются, чтобы получить комплЕксную временнУю последовательность для комплЕксного же преобразования Фурье. <-
9 Это тот самый фильтр, который авторы использовали для получения картинки реакции на линейную развёртку частоты на рис. 1.112 . <-
10 Также известный как преобразователь иммитанса (immittance ) общего вида. [* Иммитанс - понятие, обобщающее полное сопротивление и полную проводимость] . <-
11 Большая часть схем гираторов привязана к земляному потенциалу, т.е. с их помощью можно имитировать катушку, подключенную к земле, а вот плавающую индуктивность нельзя. <-
12 Или другое название – «обобщённый преобразователь иммитанса» [* общее сопротивление плюс общая проводимость] . <-
13 Выброс на вершине можно сгладить, если поставить последовательно с конденсатором в гираторе резистор с номиналом, примерно равным реактивному сопротивлению конденсатора на частоте резонанса. <-
14 Заметка по применению AB-026A за авторством Рика Даунса ( Rick Downs ). Внутреннее обозначение TI - ##sbaa001, 1991. <-
15 Подробности от SRS.
«В основе конструкции лежит лестничный LC фильтр делителе с несимметричным согласованием. Индуктивности реализованы в виде активных гираторов на паре ОУ. Лестничные фильтры на пассивных LC делителях очень спокойно относятся к точности компонентов, но из-за того, что каскады делителя связаны между собой, изменение номинала одного компонента влияет на весь делитель. Схема рассчитана таким образом, чтобы характеристики последующих ступеней изменялись сообразно и в таком направлении, при котором минимизируется воздействие на делитель в целом. Это не только позволяет снизить чрезмерные требования к точности резисторов и конденсаторов, но и делает фильтр весьма устойчивым к изменению температуры в широких пределах. В итоге использованный в SR830 спектральный фильтр удовлетворяет требованиям спецификации без какой-либо калибровки».<-
16 R. P. Sallen and E. L. Key, “A practical method of designing RC active filters,” IRE Trans. Circuit Theory, 2 (1), 74-85 ( 1955 ). <-

