7.1 (II) Генераторы

==435

7.1.5 Генераторы синусоидального сигнала

Для многих задач требуется синусоидальный сигнал, а не прямоугольный, треугольный или какой-либо иной. Примерами таких задач могут служить тестовое и измерительное оборудование для звуковых схем, радиосвязь, медицинская техника и научные приборы. Здесь часто говорят о спектральной чистоте и гармонических искажениях [* см. §7.1.10 ] , которые описывают степень отклонения сигнала от идеального синуса.

Релаксационные RC генераторы, рассматривавшиеся до настоящего момента, создавали не синусоидальный сигнал. У них на выходе естественным образом получается линейно ( или экспоненциально ) меняющееся напряжение или прямоугольный сигнал. В §7.1.4.D описывался применяемый в ИМС XR2206 метод получения приближенного к синусоидальному сигнала - последовательное сглаживание на нескольких цепях мягкого ограничения уровня. Такой же подход используется в некоторых аналоговых функциональных генераторах ²⁰. Но существуют генераторы, создающие синус непосредственно, плюс имеются методы превращения прямоугольных сигналов в синусоидальные.

Примерами генераторов синусоидального сигнала являются мост Вина ( в нём используются простые резисторы и конденсаторы ), генераторы на резонаторах ( резонансные LC контуры, кварцевые кристаллы, коаксиальные и даже атомные резонаторы ) и метод прямого цифрового синтеза ( DDS ).

В этом параграфе будут рассматриваться приёмы создания синусоидальных сигналов, начиная с получения синуса из меандра ( и прочих несинусоидальных колебаний ) и заканчивая прямой генерацией синусоидального сигнала. Чуть дальше ( §7.1.9 ) рассматриваются квадратурные генераторы , которые выдают пару сигналов со сдвигом фаз 90° .

7.1.5.A Синус из прямоугольника

Здесь надо просто пропустить прямоугольный ( или какой он там ) сигнал через ФНЧ и удалить из спектра все частоты, кроме основной. Метод очевиден, если вспомнить, что любой периодический сигнал с частотой $ f_0$ ²¹ может быть представлен в виде набора синусоидальных частотных компонент ( ряд Фурье ), причём каждая будет со своей частотой и фазой. Если сложить все компоненты вместе, то на выходе получится исходный сигнал [* следует также помнить, что набор компонент бесконечен, и потеря любого их числа приведёт к неполному восстановлению формы исходного сигнала ] . Компонента с наименьшей частотой ( имеющая тот же период, что и исходный сигнал) называется основной , а все остальные с более высокими частотами, кратными основной, - «гармониками». Множители у гармоник целые, т.е. имеем ряд 2$ f_0$ , 3$ f_0$ , и т.д. Таким образом, периодический сигнал произвольной формы можно привести к синусоидальному, пропустив через ФНЧ со срезом, лежащим выше основной частоты $ f_0$ , но ниже второй гармоники 2$ f_0$ ²². В такой схеме будет выделена только основная синусоидальная компонента.

==436

Если фильтр способен задержать большую часть высокочастотного спектра, то на выходе будет неплохой синусоидальный сигнал. В Части _6 говорилось, что фильтры нижних частот можно делать по-разному. Можно собрать пассивный фильтр «непрерывного времени» из набора отдельных индуктивностей и емкостей, либо, если речь идёт о достаточно низкой частоте, по схеме активного фильтра, либо фильтр «дискретного времени» на переключаемом конденсаторе, либо чисто математическими методами цифровой обработки сигналов.

В качестве иллюстрации соберём генератор с частотой 1 kHz на 555 ( по схеме 7.10 A с $R$=75 kΩ и $ C $=10 nF ) и поставим ему на выходе активный ФНЧ непрерывного времени ( «Баттерворт» 8-го порядка ) со срезом на частоте 1.5 kHz . Результат выглядит довольно прилично, а измерения дают 0.6% искажений ²³. Такой путь предполагает построение достаточно сложных электронных схем и не позволяет «играть» частотой ( выбор частоты среза ограничивает возможность перестройки генератора диапазоном ±25% ).

Фильтры на переключаемом конденсаторе гораздо проще в использовании и, к тому же, доступны в виде дешёвых ИМС. Вместо R и C для задания полосы пропускания используется тактовая частота. Именно она определяет частоту среза. На рис. 7.18 приведена схема простого устройства, в котором фильтр на переключаемом конденсаторе MAX294 превращает прямоугольный сигнал в синусоидальный. Частота среза MAX294 равняется $ f_{CLK}$/100 , поэтому на тактовый вход подаётся частота в 128 раз большая, чем требуемый сигнал. Частота среза при этом равна 1.28×$ f_{IN}$ . Результат работы схемы показан на рис. 7.19 . Измеренный уровень искажений составляет 0.03% .

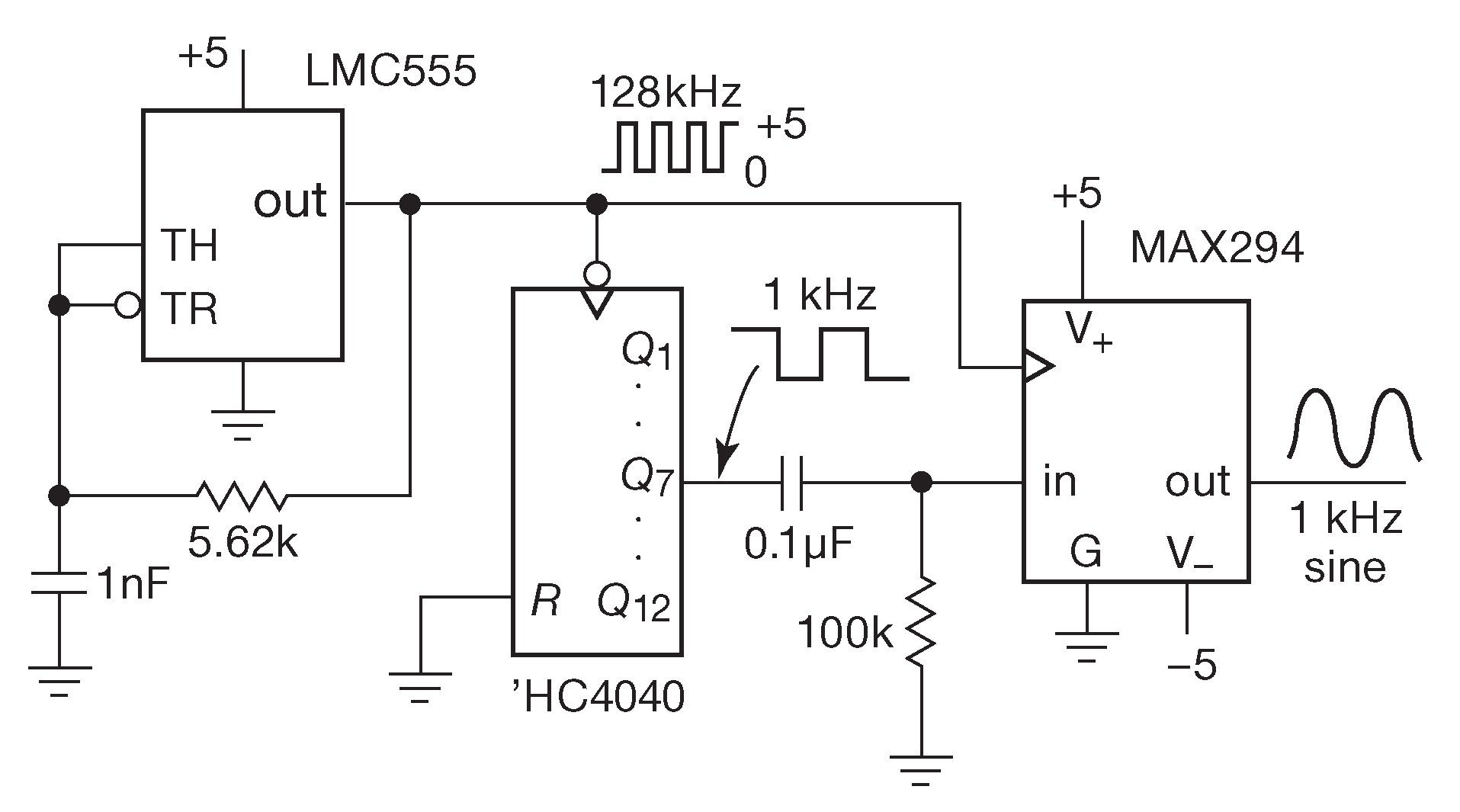
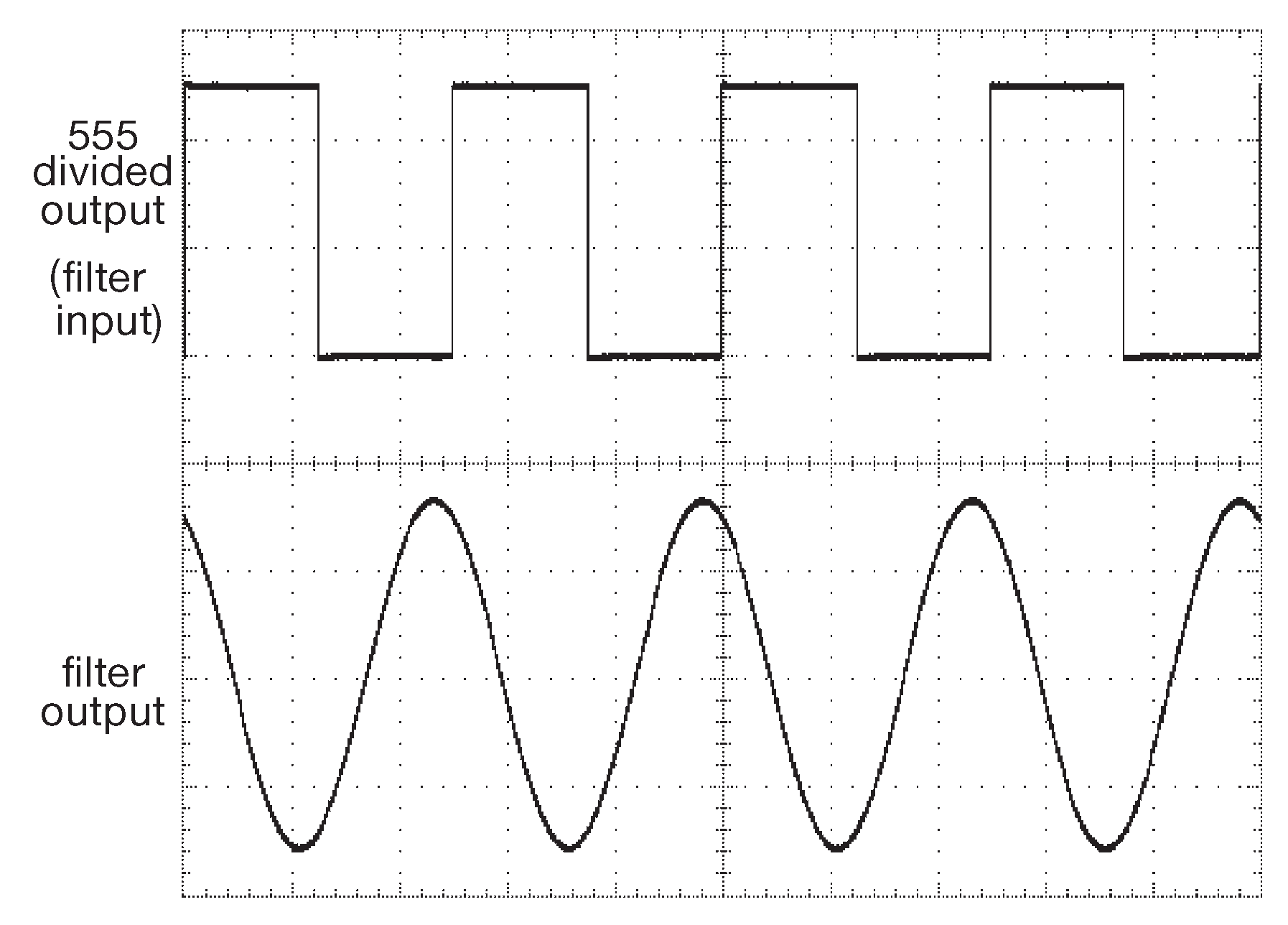
Рис.7.18 Генератор синусоидального сигнала на следящем фильтре низких частот. MAX294 ( или аналогичный MAX293, или LTC1069-1 ) - это эллиптический фильтр 8-го порядка на переключаемом конденсаторе, которому не нужны внешние компоненты
Рис.7.19 Сигналы в схеме 7.18 : прямоугольный сигнал 1 kHz ( $ f_{OSC}$/128 ) на входе и синусоидальный после фильтра нижних частот, амплитуда которого равна уровню основной частотной компоненты входного меандра, т.е. в 4/π раз больше. По горизонтали 400 μs/div , по вертикали 2 V/div

Данная схема не только проще, чем аналоговый вариант, она обеспечивает предсказуемую амплитуду на выходе ²⁴ и возможность настройки. Последнее свойство становится возможным, потому что фильтр управляется частотой на тактовом входе ( отслеживает её). Характеристическая точка устанавливается на уровне 1.28×$ f_{IN}$ независимо от изменения частоты на входе ²⁵. Диапазон изменения частоты 555 в данном устройстве равен 10 , изменения уровня искажений в диапазоне от 100 Hz до 100 kHz не превышает 0.1% .

7.1.5.B Мостовой генератор Вина

Для низких и средних частот очень удобным источником синусоидального сигнала с малыми искажениями служит мостовой генератор Вина ( рис. 7.20 ). Идея заключается в создании усилителя с обратной связью, имеющей на нужной частоте сдвиг фазы 0° . Осталось подстроить усиление в петле обратной связи так, чтобы появились самоподдерживающиеся колебания. Для одинаковых величин $R$ и $ C $ усиление по напряжению должно в точности равняться +3.00 . Для меньших значений колебания будут затухать, а для больших выход будет насыщаться ( ограничиваться на уровнях питания ). Пока усилитель находится в линейном режиме, искажения будут низкими. Иначе говоря, нельзя допускать полного размаха сигнала. Без целенаправленного контроля усиления, сигнал на выходе будет расти до тех пор, пока общее усиление не снизится до 3.0 за счёт ограничения. Предлагается контролировать усиление с помощью обратной связи с большой постоянной времени.

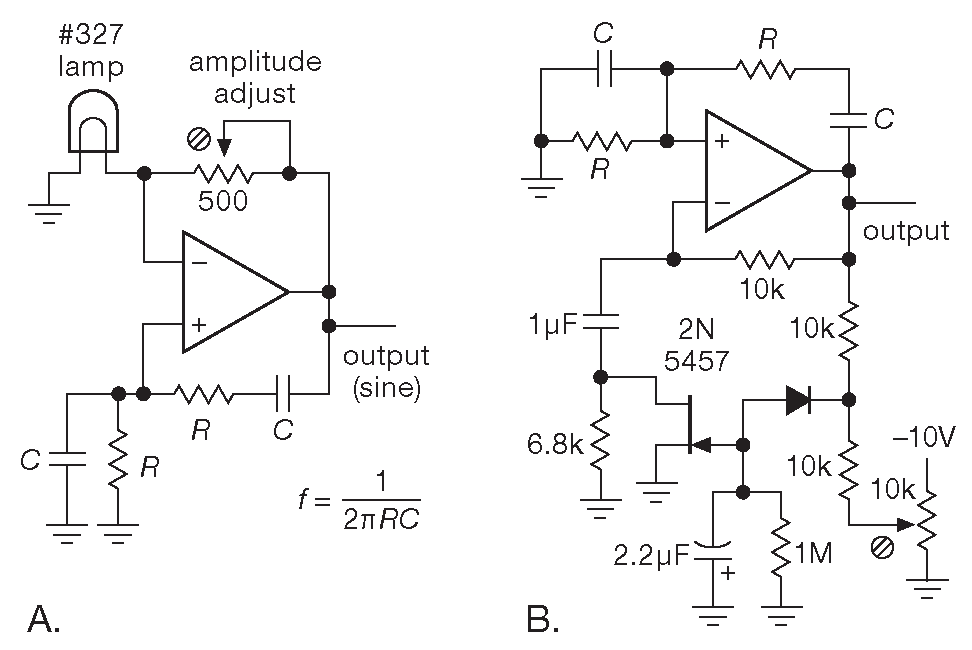
Рис.7.20 Генератор Вина с малыми искажениями. (A) Регулирование амплитуды с помощью лампы накаливания. (B) Регулирование амплитуды с помощью переменного резистора на полевом транзисторе с p-n переходом

==437

В первой схеме в качестве элемента обратной связи с переменным сопротивлением используется лампа накаливания. Рост выходного напряжения вызывает небольшой нагрев нити накаливания, увеличивает её сопротивление, и, соответственно, чуть уменьшает усиление в неинвертирующем включении. Для звуковых частот выше 1 kHz схема имеет менее 0.003% искажений. Дополнительные детали можно найти в заметке по использованию ##AN5 ( 12/84 ) и ##AN43 ( 6/90 ) фирмы LTC ²⁶.

На второй схеме амплитудный дискриминатор, состоящий из делителя и диода, заряжает RC цепочку с большой постоянной времени. Напряжение на затворе управляет усилением, регулируя сопротивление канала полевого транзистора. Для небольших изменений напряжения полевой транзистор ведёт себя подобно переменному сопротивлению ( см. §3.2.7 ). Большая постоянная времени ( здесь 2 секунды ) нужна, чтобы подавить искажения, потому что быстрая обратная связь будет искажать форму выходного сигнала, пытаясь регулировать его амплитуду внутри каждого периода частоты.

Ещё один интересный способ управления амплитудой показан на рис. 7.21 , где обратная связь по усилению замыкается через фоторезистивную оптопару. Она состоит из излучающего светодиода и резистивного фотоэлемента, обеспечивающих хорошую линейность ( < 0.1% искажений для приложенного напряжения < 1 Vrms ) в полосе нескольких декад сопротивления в соответствии с током светодиода. В отличие от кремниевых компонентов фотоэлемент - штука небыстрая по самой своей природе ( для использованной модели - десятки миллисекунд ), что в данном случае только в плюс.

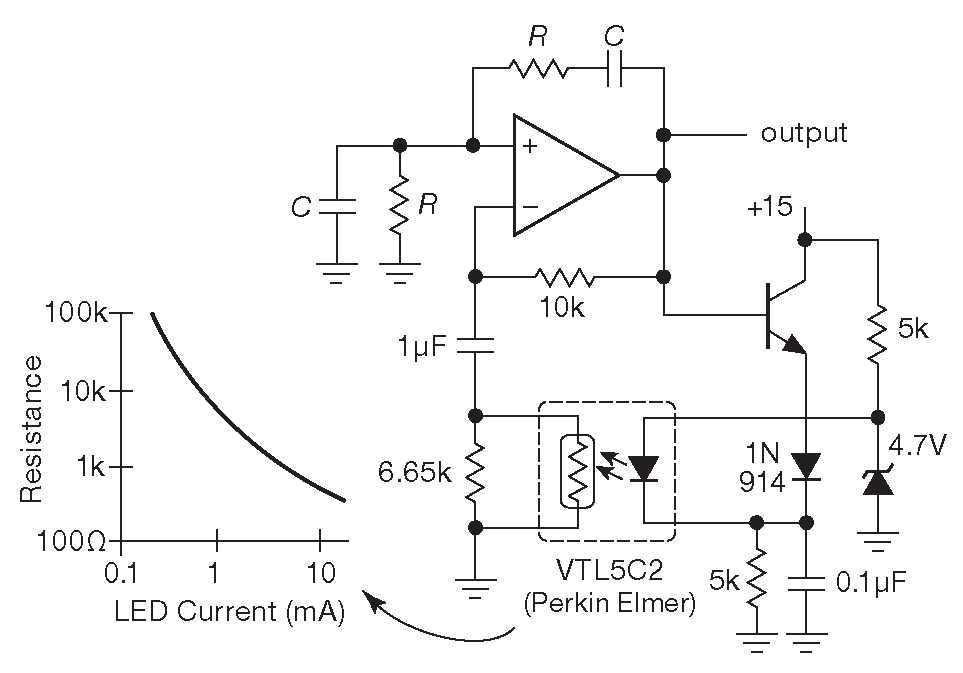
Рис.7.21 Фоторезистивная оптопара предоставляет ещё один способ управления амплитудой мостового генератора Вина ( с любезного разрешения Стива Сёвина ( Steve Cerwin ))

Автор заявляет, что аккуратная конструкция позволяет снизить искажения до долей ppm . Для таких цифр требуется высокий коэффициент усиления ( т.е. композитная схема ) и подавление остаточных искажений. Подробности можно узнать в Linear Technology Magazine, Feb. 1994, стр. 26-28.

Схема со сверхнизкими искажениями

Авторы скептически относятся к подобным заявлениям ²⁷. Но, так или иначе, внимание к деталям позволяет дотянуться до единиц ppm ( 0.0001% ), используя достаточно распространённые компоненты и приёмы. На рис. 7.22 показана схема, которая была разработана и протестирована в рамках проверки данного утверждения.

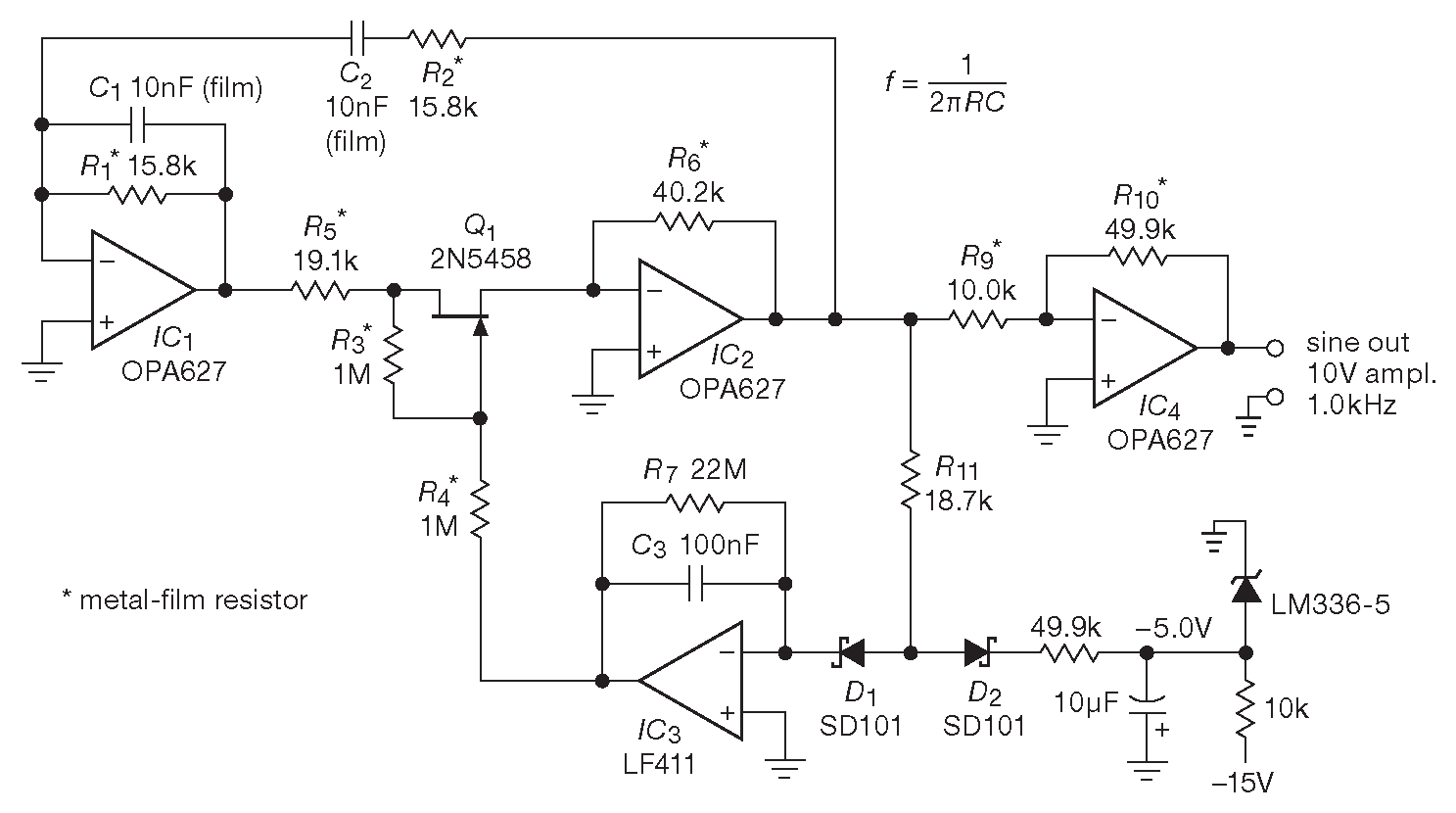
Рис.7.22 Мостовой генератор Вина ( 1 kHz ) с необычайно низкими искажениями ( < 0.001% ). Для достижения наилучших параметров в состав $R_5$ включён подстроечный потенциометр, позволяющий оптимизировать регулирующее сопротивление ПТ $Q_1$

Разработка началась со схемы на двух ОУ, использовавшей преимущества инвертирующего включения: снижение искажений за счёт исключения синфазных составляющих, всегда присутствующих в неинвертирующей схеме. За основу взят OPA627. Это быстрый ( $ f_T $=16 MHz ), малошумящий ( $e_n$=4.5 nV/$\sqrt{Hz}$ ) усилитель с низким входным током ( $I_B$≈1 pA ), имеющий основное преимущество в виде исходно низких искажений ( 0.00003% ) в схеме повторителя для сигнала 10 V@1 kHz и способный работать при ±15 V . В данной задаче предпочтительно работать именно с большими сигналами, чтобы уменьшить влияние шума на чистоту сигнала.

==438

Для такой схемы незатухающие колебания появляются при усилении по напряжению в $IC_2$ на уровне –2.00 . Номинал $R_5$ выбран на 5% ниже критического, с тем чтобы последовательно включённый ПТ работал управляемым переменным сопротивлением 1 kΩ . На транзистор подаётся синусоидальный сигнал 100 mV ( пик-пик ), который достаточно мал, чтобы транзистор оставался в линейной области. Кроме того, затвор подключается через линеаризирующий делитель $R_3R_4$ ( §3.2.7.A ). Амплитудой управляет интегратор $IC_3$ , на который приходят импульсы тока с делителя, подключённого к опорному уровню –5V . Ток возникает, когда сигнал на выходе $IC_2$ достигает 2V . Идущий в отрицательную область сигнал с интегратора [* интегратор инвертирует полярность ] смещает затвор ПТ вниз относительно потенциала виртуальной земли на истоке. Сопротивление канала транзистора при этом растёт, снижая усиление $IC_2$ и пытаясь стабилизировать выход по амплитуде ²⁸. Для указанных номиналов минимальное сопротивление ПТ ( т.е., при $ V_{GS}$=0 ) $R_{ON}$ должно быть меньше 1 kΩ , что требует минимальной крутизны $ g_m$=1 mS ( см. §3.2.7 ). Паспортные данные на 2N5458 указывают минимальную крутизну $ g_m$=1.5 mS , что гарантирует автоматический запуск генератора. Авторы пристегнули инвертирующий каскад с G=5 , чтобы получить на выходе удобную для работы амплитуду 10 V .

Схема работает «из коробки» [* отечественный эквивалент: «правильно собранная схема в наладке не нуждается»] . Она сразу выдаёт правильную частоту и амплитуду ( 1 kHz@10 V ) и правильную форму сигнала. Измеренное значение THD ( общие искажения ) составляют 0.002% ²⁹. Прежде чем праздновать успех, были опробованы следующие варианты.

Плёночный конденсатор заменялся керамическим ( с диэлектриком X7R ). При этом гармоники возрастали на два порядка до 0.22% ! ³⁰.
Амплитуда сигнала на ПТ уменьшалась до 50 mVpp ( $R_5$ увеличивался до 19.6 kΩ ), что в два раза снижало искажения - до 0.001% . Данное изменение было оставлено в рабочей схеме, и дальнейшие эксперименты шли уже с ним.
Отношение $R_3/R_4$ было подправлено для уменьшения амплитуды второй гармоники ( основной вклад в искажения ). Уровень THD снизился до 0.0002% , т.е. до –114 dB от уровня сигнала или до двух частей на миллион ( 2 ppm ).
Наконец, чтобы оценить эффект от линеаризирующего делителя в затворе был исключён $R_4$ . Искажения подскочили в 50 раз до 0.01% .

Некоторые важные выводы. Если нужны возможно меньшие искажения, необходимо:

избегать дешёвых керамических конденсаторов,
использовать линеаризирующие цепи в затворе ( вычитать $ V_{DS}$/2 из $ V_{GS}$ ) , и
уменьшать сигнал на ПТ в режиме переменного резистора, желательно, ниже 100 mV ( но это вызовет рост времени установления амплитуды ).

Основной вклад в искажения, даже после подстройки, вносит нелинейность полевого транзистора, поэтому снизить THD в ещё большей степени можно, уменьшая рабочую амплитуду генератора до, скажем, 0.5 V . Цена вопроса - увеличение относительной доли широкополосного шума операционного усилителя, имеющего фиксированный уровень ³¹.

7.1.5.C RC генератор на сдвиге фаз

==439

В отличие от релаксационного генератора, в котором постоянная времени $RC$ вместе с пороговым переключением напряжения создаёт колебания, генератор Вина использует фазосдвигающие свойства RC цепи в схеме с положительной обратной связью, которая выбирает рабочую частоту. Та же идея лежит в основе генераторов на сдвиге фаз : цепочка из нескольких резисторов и конденсаторов охватывается обратной связью с усилением. Итоговая частота колебаний определяется временными свойствами RC цепи, см. рис. 7.23 .

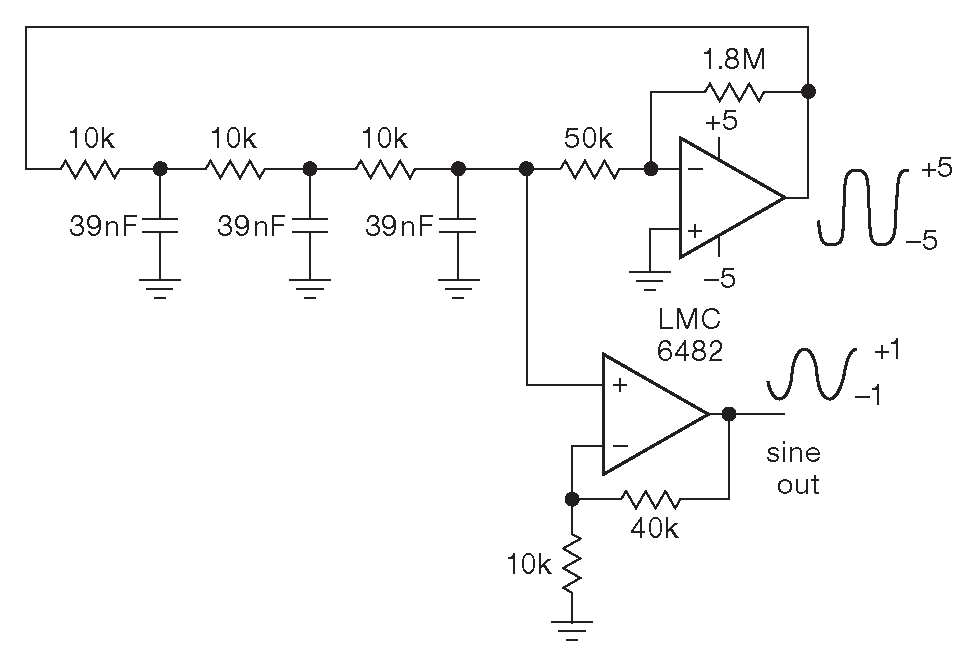
Рис.7.23 Генератор на сдвиге фаз. Три RC секции создают сдвиг фаз 180° , который превращается в положительную обратную связь инвертирующим усилителем

Три RC секции вызывают запаздывание фазы, которое увеличивается с ростом частоты, достигая 180° при $ω$=2.4/($RC$) , причём RC цепочки ослабляют сигнал в 26 раз ³². Оставшиеся 180° добавляет инвертирующий усилитель, он же восполняет потерю амплитуды ( здесь используется консервативное значение G=–36 ). Схема возбуждается на частоте 1 kHz , формируя обрезанный синусоидальный сигнал с достаточно большими искажениями, достигающий уровней питания ±5V . На выходе последней RC секции сигнал уже вполне синусоидальный, а после вспомогательного усилителя 5× достигает амплитуды ±1V и имеет искажения на уровне 0.9% .

Для фанатов генераторов на сдвиге фаз есть масса вариантов: на дискретных транзисторах, с обратной связью с ограничением по амплитуде и т.д. Приведём ещё один генератор, построенный по этому принципу ( рис. 7.24 ). Здесь как всегда инвертирующий интегратор даёт задержку фазы 270° , поэтому нужны только две RC секции, чтобы замкнуть обратную связь с нужной фазой. Амплитуда ограничивается встречно параллельно включёнными диодами. Как и в схеме 7.23 , сигнал снимается с последней секции, где искажения минимальны. Схема выдаёт синусоидальный сигнал 1 kHz@1V с искажениями 1% . Если диодный ограничитель передвинуть и поставить параллельно первому конденсатору 39 nF , то на выходе интегратора сигнал станет синусоидальным, но с фазой, задержанной на 90° относительно выходного ( т.е. он будет инвертированным косинусоидальным ). В итоге схема будет давать «квадратурную пару» ( §7.1.9 ), но с разными амплитудами.

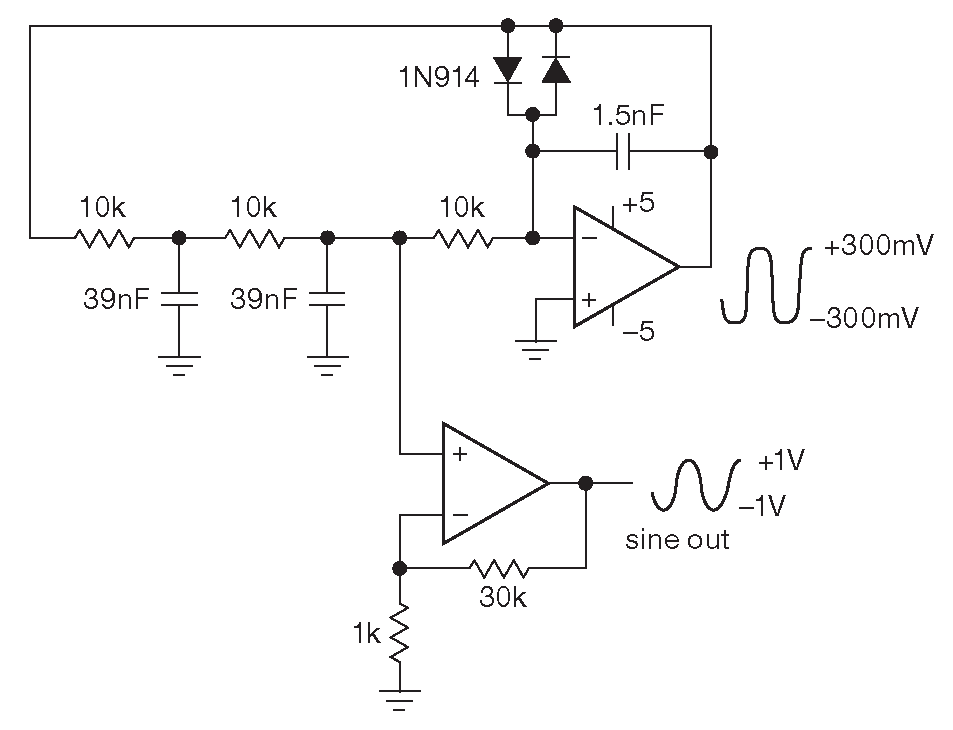
Рис.7.24 Вариант генератора на сдвиге фаз. Интегратор добавляет 90° к задержке фазы ( и инвертирует её) после двух RC секций. ( С разрешения Тони Вильямса ( Tony Williams ))

7.1.5.D LC генераторы

На высоких частотах ( выше мегагерца ) преимущественным методом получения синусоидальных сигналов становится использование резонансных цепей. Резонаторы могут быть электрическими ( LC цепи ), электромеханическими ( пьезоэлектрические кварцевые кристаллы ) и даже атомно-молекулярными ( устройства на парах рубидия или атомах водорода ). Некоторые из резонаторов настраивать легко ( LC ), частоты других фиксированы достаточно жёстко ( кварцевые кристаллы ). Резонансные генераторы принципиально отличаются от описанных ранее RC схем. Они основаны на элементах, изначально имеющих некоторую резонансную частоту, в то время как RC цепи являются нерезонансными времязадающими и фазосдвигающими элементами. Т.к. резонансы могут быть очень узкими по частоте и стабильными во времени, они хорошо подходят для построения источников опорной частоты.

Разговор начнётся с LC генераторов, которые играют важную роль в связных устройствах. В таких схемах настроенные LC контуры подключаются к усилителю, который обеспечивает усиление на частоте резонанса, а общая положительная обратная связь поддерживает незатухающие колебания. Такие конструкции запускаются автоматически.

==440

Две популярные схемы приведены на рис. 7.25 . Первая называется генератором Колпитца ³³ и состоит из параллельного LC контура на входе с положительной обратной связью с выхода ( фаза инвертируется на полевом транзисторе ). Схема настроена на 20 MHz , искажения составляют –60 dB . Вторая схема - генератор Хартли на npn транзисторе. Частота настраивается конденсатором переменной ёмкости. Схема с общей базой сигнал не инвертирует, поэтому и сигнал обратной связи имеет прямую полярность. Обе схемы используют трансформаторную развязку : буквально несколько витков провода работают как понижающий трансформатор.

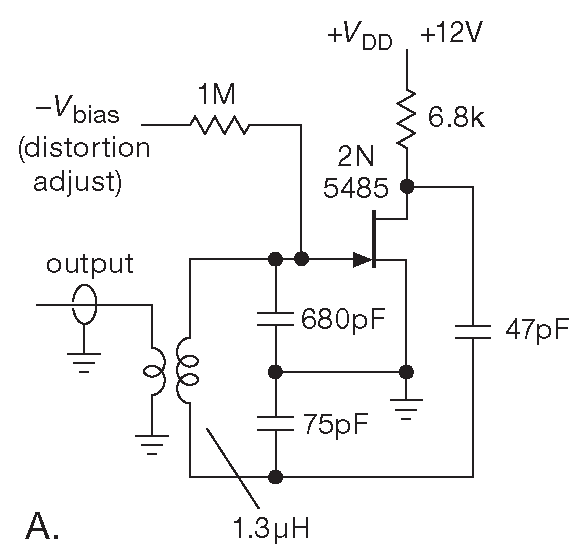
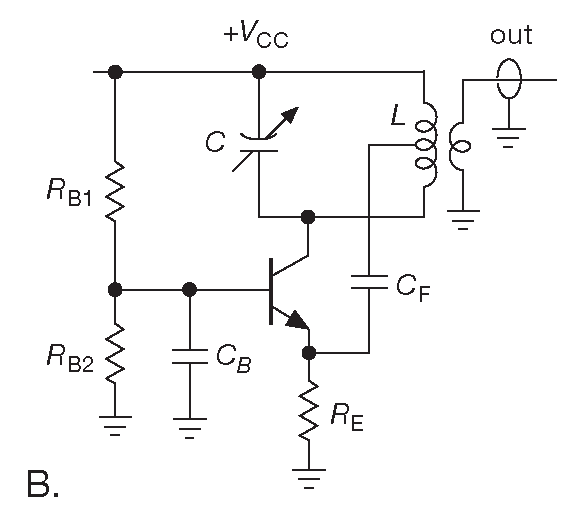
Рис.7.25 Популярные схемы LC генераторов. (A) Генератор Колпитца на конденсаторе с центральным отводом. (B) Генератор Хартли на индуктивности с центральным отводом

Третья схема ( рис. 7.26 ) - генератор с эмиттерной связью ( генератор Пельца ) на элементе ’1648 из цифрового семейства ECL III – «генераторе, управляемом напряжением» ³⁴. Схему можно рассматривать в качестве неинвертирующего дифференциального усилителя с обратной связью. Частоту задаёт резонанс параллельного LC контур, который равен $ f_0=1/( 2π\sqrt{LC} ) $. Рабочий диапазон достигает 200 MHz . Справочные данные сулят «высокую спектральную чистоту», но авторы находят её в лучшем случае средней, если сравнивать с генератором Клаппа на ПТ ( см. схему 7.29 и графики на рис. 7.30 ).

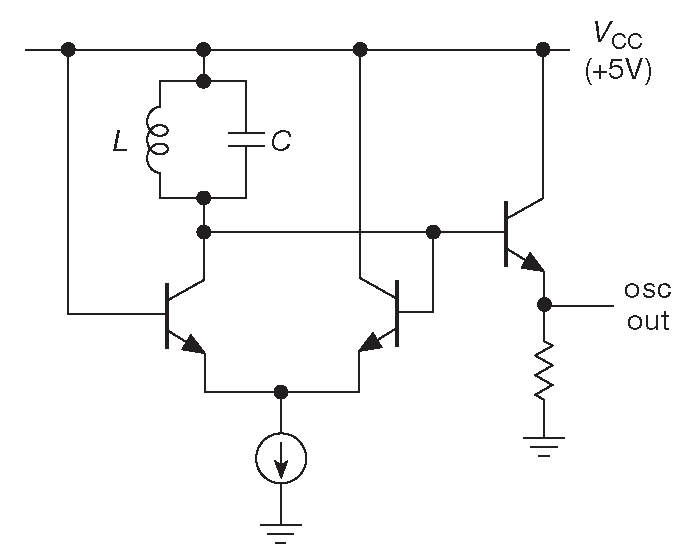
Рис.7.26 Генератор на эмиттерно-связанной логике. Это упрощённая версия ИМС MC1648 из логического семейства ECL III

Электрическая настройка

LC генератор можно настраивать в некоторых пределах электронными методами. Для таких задач в резонансный контур вставляют «конденсаторы, управляемые напряжением» ( варакторы ). Физически таким конденсатором является обратно смещённый диод: ёмкость p-n перехода снижается по мере роста обратного напряжения ( ##§1.9.5.B bad_link ). В качестве варактора может работать любой диод, но можно взять модель, специально предназначенную для этой задачи. Характеристики нескольких ярких представителей приведены на рис. 7.27 , а на рис. 7.28 показано, как реализовать электрическую подстройку ±1% на варакторе ( в примере приводится генератор Армстронга на ПТ с трансформаторной связью с истока ). Диапазон подстройки принудительно сужен, чтобы улучшить стабильность. Именно поэтому конденсатор фиксированной ёмкости имеет номинал 100 pF , а варактор - 15 pF . Отметим большой номинал смещающего резистора ( чтобы ток смещения не нагружал генератор ) и блокировочный конденсатор.

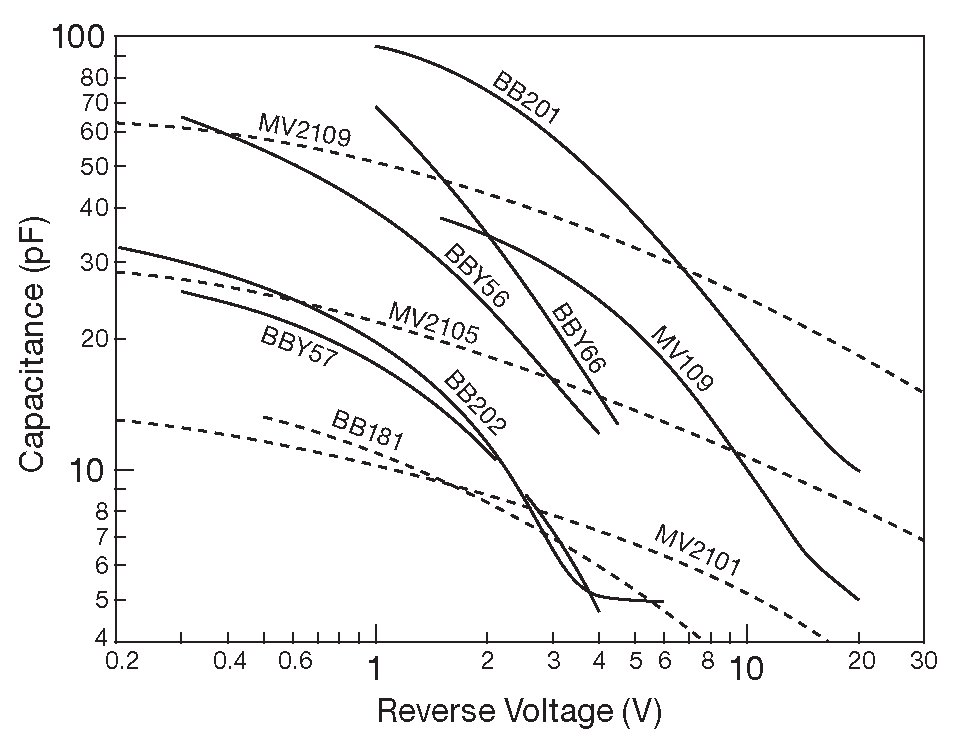
Рис.7.27 Обратно смещённые диоды имеют ёмкость перехода, которая зависит от приложенного напряжения. На графике показаны параметры некоторых настроечных диодов – «варакторов». Изогнутые сплошные линии характерны для моделей со «слишком резким», близким к обычным диодам поведением

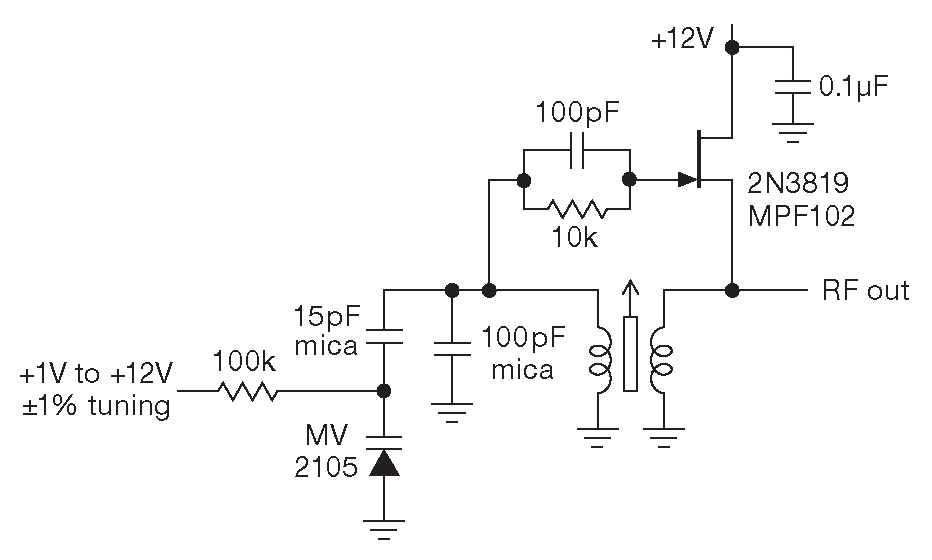
Рис.7.28 LC генератор с варакторной подстройкой

Типичные варакторы имеют максимальную ёмкость в районе от нескольких пикофарад до нескольких сотен пикофарад, а диапазон её изменения примерно 3:1 ( хотя встречаются модели с отношением, доходящим до 15:1 ). Резонансная частота LC контура обратно пропорциональна квадратному корню из ёмкости, поэтому максимальные величины перестройки оставляют 4:1 , а типовые цифры ближе к ±25% .

==441

В схемах на варакторах резонатор ( и цепи подачи постоянного управляющего смещения ) подключается непосредственно к варактору, с тем чтобы изменение ёмкости последнего прямо влияло на частоту. Такой способ управления несколько искажает форму колебаний и, что важнее, привносит определённую зависимость частоты колебаний от их амплитуды. Чтобы минимизировать эффект, амплитуду колебаний следует ограничивать и повышать её позднее, если требуется. Кроме того, стоит подавать на варактор возможно больший смещающий потенциал ( более вольта ), чтобы напряжение генерации выглядело небольшим на его фоне.

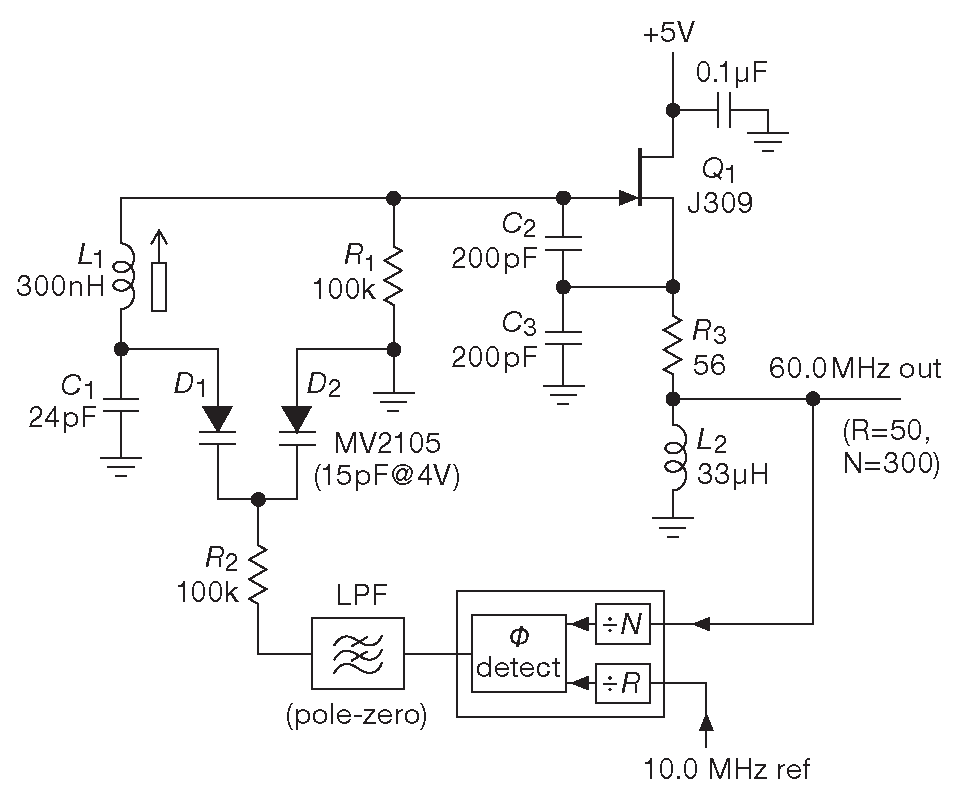
Рис.7.29 Малошумящий LC генератор на полевом транзисторе, используемый в схеме фазовой автоподстройки частоты ( см. §13.13 ). Данная схема имеет очень высокое подавление боковых полос, что хорошо видно по спектру на рис. 7.30

Дополнительным приёмом, позволяющим снизить эффект «амплитуда-частота», является использование пары встречно включённых варакторов, которые будут менять свою ёмкость в противоположных направлениях. Подход иллюстрируется схемой 7.29 ( см. также рис. 6.8 ). На ней изображён малошумящий генератор, который стоит в петле фазовой автоподстройки ( §13.13 ) и играет роль «местного генератора» , обеспечивая приёмник радиотелескопа чистым сигналом 60 MHz . Генератор собран по схеме Клаппа. Частота задаётся последовательной цепью $L_1C_1$ , причём параллельно $ C_1 $ стоят два встречно соединённых варактора. Управляющий потенциал подаётся через $R_2$ . Оба диода при этом смещаются в обратном направлении ( относительно заземлённых анодов ). На каждый из варакторов одинаковой ёмкости приходится половина амплитуды колебаний, но почти одинаковое изменение емкостей ( если, конечно, сигнал не слишком велик ) идёт в разных направлениях. Итоговое изменение по большей части нивелирует изменение общей ёмкости последовательной пары, а значит, и искажения вместе с подёргиваниями частоты. Измеренный уровень чистоты сигнала примерно на 10 dB лучше, чем у хорошего коммерческого синтезатора частоты HP3325A. На рис. 7.30 приведён выходной спектр. Для сравнения показан сигнал с MC1648 с эмиттерно-связанным генератором с такими же LC компонентами и с такой же рабочей частотой ³⁵.

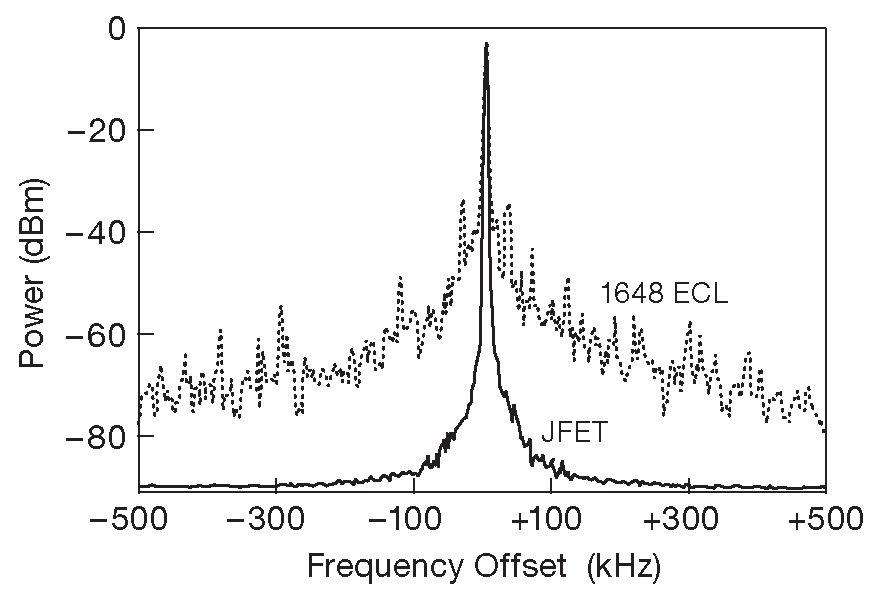
Рис.7.30 Частотный спектр генератора на полевом транзисторе с рис. 7.29 в сравнении с биполярным генератором на ECL элементе MC1648. По горизонтали 200 kHz/div , по вертикали 10 dB/div

Генераторы с электрическим управлением активно используются в частотной модуляции и схемах фазовой автоподстройки радиочастотного диапазона, подобных приведённой. Теме ФАПЧ посвящена глава в Части 13 .

Для общего образования следует упомянуть близкого родственника LC генераторов, называемого «генератором камертонного типа» . Он использует высокодобротные колебания настроенной металлической вилки [* двузубой] в качестве частотозадающего элемента. Такая конструкция находит применение в качестве низкочастотных стандартов ( и позволяет получить стабильность на уровне единиц ppm в термостатированной среде ) и механических часах [* и, добавим, в музыке - те самые «камертоны»] . В электронике данная конструкция была вытеснена кварцевыми резонаторами, которые рассматриваются ниже ( §7.1.6 ). Интересно, что низкочастотные кварцевые кристаллы ( например, на «часовую» частоту 2¹⁵=32'768 Hz ) колеблются в механическом камертонном режиме.

==442

7.1.5.E Паразитные генераторы

Предположим, вы только что собрали отличный усилитель и подали на вход синусоидальный сигнал и наслаждаетесь чистым синусом на выходе. Вы переключаете генератор в режим прямоугольного сигнала, но на выходе усилителя по-прежнему синус! Внезапно! Оказывается, это не усилитель, а одна большая проблема.

Паразитное возбуждение не всегда столь очевидно, как в описанном случае. Часто оно проявляется как размытость формы некоторой части сигнала, как неправильная работа источника тока, необъяснимое смещение операционного усилителя, или отличная работа с подсоединённым щупом осциллографа и неправильное поведение в его отсутствие. Все эти аномалии - свидетельство паразитного высокочастотного возбуждения незваного генератора Хартли или Колпитца, которые самозарождаются в резонансных контурах, образованных индуктивностями выводов и межэлектродными емкостями.

Схема на рис. 7.31 показывает, как источник тока может превратиться в генератор. Такая конфигурация сложилась на одной из лабораторных работ, когда параметры стандартного источника тока начали измерять древним стрелочным авометром. Ситуация выглядела как слишком сильное ( 5..10% ) изменение тока при изменении напряжения питания в рабочих пределах, причём проблема «излечивалась» простым прикосновением к выводу коллектора. Ёмкости измерительной головки и перехода коллектор-база транзистора образовывали резонансный контур с индуктивностью той же самой измерительной головки и запускали классический генератор Хартли, обратную связь в котором обеспечивала ёмкость коллектор-эмиттер. Небольшой резистор последовательно с базой снижал высокочастотное усиление в схеме с общей базой и подавлял тем самым генерацию. Это, кстати, один из возможных методов борьбы с напастью.

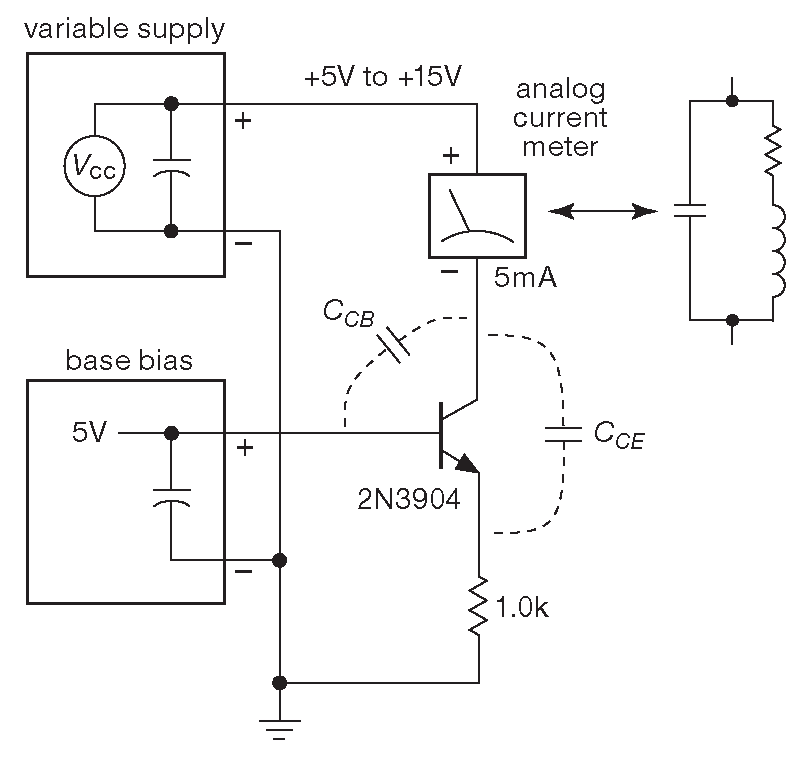
Рис.7.31 Самозародившийся генератор Хартли мешает работе источника тока

Предпосылкой для возникновения паразитного возбуждения является наличие усиления в активных цепях. Следует немедленно насторожиться в случае неожиданного и странного поведения таких схем. Иногда можно видеть признаки возбуждения на каких-то конкретных участках сигнала. По мере накопления опыта становятся заметнее симптомы возбуждения ОУ ( обычно в окрестностях $ f_T $ , т.е. где-то в районе мегагерц ) или малосигнальных транзисторов ( на десятках и сотнях мегагерц ).

«Наводки»

Очень легко ³⁶ ошибиться, приняв за генерацию наводки самых разных видов. Они также вызывают искажение и размытие формы сигналов. Если есть подозрение на наличие наводок, то следует, во-первых, проверить их на совпадение с частотой силовой сети ( 60 или 120 Hz ³⁷), что является чётким признаком сетевой наводки [* ##бывают варианты, к счастью, редко] . Каналом передачи обычно служит емкостная связь с какой-либо высокоомной точкой схемы или индуктивная связь цепи, образующей контур, через который проходят линии внешнего магнитного поля. Третья возможность - контуры в цепи земли ( различные части схемы, опирающаяся на местные потенциалы земли, которые неожиданно оказываются не равны между собой ). Даже в хорошо разведённой печатной плате последняя причина может доставить серьёзные проблемы, когда к прибору подключается внешнее устройство, которое запитывается от другой электрической розетки. Высокочастотные наводки тоже достаточно распространённое явление. Чаще всего их распространяют ключевые источники питания ( они рассматриваются в Части _9 ), и в этом случае частота наводки лежит в диапазоне 20 kHz...1 MHz . Кроме того, речь может идти о радиочастотных наводках от теле- и радио-вещательных станций ( для США это диапазоны 0.5–1.7 MHz для AM, 88–108 MHz для FM и 55–700 MHz для телестанций ).

==442

²⁰ Такой способ «порчи» треугольного сигнала диодным ограничителем даёт посредственный синус, его искажения редко опускаются ниже 1% . Для сравнения, аудиофилы требуют усилителей с уровнем искажений ниже 0.1% . Чтобы проверять компоненты звукового тракта с такими параметрами, требуется источник чистого синусоидального сигнала с остаточными искажениями ниже 0.01% . <-

²¹ Ладно, ладно, почти любой. Математики мастера находить всякие вырожденные функции, чтобы оспорить любые недостаточно точно определённые утверждения. В данном случае следовало бы написать что-нибудь типа: «Любой добропорядочный ( well-behaved ) периодический сигнал». Впрочем, можно сформулировать смелее: «Любой периодический сигнал, который можно воспроизвести с помощью электронного устройства». <-

²² Для симметричных сигналов в зависимости от вида симметрии ряд Фурье может состоять только из нечётных гармоник. В таком случае первой гармоникой будет 3$ f_0$ . Для меандра ( прямоугольного сигнала со скважностью 50% ) имеет место именно такое разложение. <-

²³ Установление среза на частоте 1.2 kHz снижает искажения до 0.1% или до -60 dBc ( dB-to-carrier ). <-

²⁴ Она определяется первым членом разложения Фурье, и для прямоугольного сигнала $ A(pp)=(4/π)Vcc$ или 2.25 Vrms . <-

²⁵ Очень интересный вариант схемы приводится в справочных данных на LTC1799. Там следящий ФНЧ на переключаемом конденсаторе представлен в виде фильтра-пробки с частотой задержания 3$ f_0$ , чтобы дополнительно ослаблять самую мощную гармонику в прямоугольном сигнале. <-

²⁶ Возможность использования лампы для стабилизации генератора Вина была обнаружена и запатентована (#2,268,872 ) Вильямом Хьюлиттом ( William Hewlett ) в 1942г. Итогом исследования стал коммерческий звуковой генератор 200 A, который Хьюлитт продавал в партнёрстве с Дэвидом Паккардом ( David Packard ) за $54.40. Интересно, что цена появилась не в результате бухгалтерских расчётов. Просто партнёрам нравился слоган «54-40 или война!», который кандидат в президенты Полк использовал в северо-западных штатах США. Такая вот история. <-

²⁷ Авторы рекомендуют относиться с благоразумным скепсисом к любым заявлениям о суб-ppm параметрах аналоговых схем. <-

²⁸ Усиление интегратора подбиралось таким образом, чтобы частота единичного усиления петли обратной связи составляла примерно 50 Hz . <-

²⁹ Практически исключительно вторая гармоника. <-

³⁰ Теперь доминирует третья гармоника. <-

³¹ Более того, используя фоторезистивное управление, аналогичное схеме 7.21 Джим Вильямс добился снижения измеренных искажений до 3 ppm . Он добавил фильтр нижних частот между $IC_3$ и $R_4$ , чтобы уменьшить изменение сигнала ошибки с интегратора между циклами, см. LTC ##AN132. <-

³² Воздействие нагрузки вызывает отклонение от идеальных цифр, т.е. параметров полностью изолированных секций, которые равны $ω=\sqrt{3}/( RC) $ для частоты и 8 для коэффициента ослабления. <-

³³ Эдвин Колпитц ( Edwin H. Colpitts ), US patent 1624537. Заявка подана 1918г., но выдана только в 1927. <-

³⁴ На самом деле это просто генератор , а чтобы менять настройку потребуется внешний варактор, включённый по показанной выше схеме. <-

³⁵ Чтобы сохранить спектральную чистоту генератора после встраивания его в петлю обратной связи ФАПЧ, была добавлена LC ловушка, которая давит выбросы с частотой опорного генератора ( 200 kHz ) с фазового детектора. См. рис. 6.8 . <-

³⁶ Это проще, чем можно подумать, потому что, помимо всего прочего, данное явление вызывает появление «фантомных сигналов» в цифровых осциллографах. <-

³⁷ 50 и 100 Hz , если речь идёт не об обеих Америках или некоторых других анклавах 60-герцовой сети. <-