7.1 (IV) Генераторы
==450
7.1.7 Генераторы высокой стабильности TCXO, OCXO и далее
Получить частоту со стабильностью несколько частей на миллион для обычного температурного диапазона [* вероятно, речь идёт о 0...70°C ] можно без каких-либо затруднений с помощью кварцевого резонатора. Задействовав схему с температурной компенсацией можно сделать TCXO - температурно компенсированный кварцевый генератор с более высокими параметрами. Законченные TCXO и обычные генераторы выпускают многие производители, например, Bliley, Cardinal Components, CTS Knights, Motorola, Reeves Hoffman, Statek, Vectron. Оформление может быть самым разным: от специализированных блоков до модулей размером с корпус микросхемы, в том числе и для поверхностного монтажа. TCXO дают 1 ppm в диапазоне 0...50°C ( дешёвые модели ) и 0.1 ppm или лучше при той же температуре ( дорогие ).
7.1.7.A Термостабилизированные генераторы
Для особо высокой стабильности потребуются кварцевые генераторы с термостатированием . В них используется кристалл с нулевым температурным коэффициентом, подогретый до температуры 80...90°C , за стабильностью которой присматривает специальная схема. Такие генераторы выпускаются в виде выводных модулей для внутриприборного монтажа и в виде законченных блоков. Примером может служить модуль 1000B фирмы Symmetricom. Это генератор на 10 MHz со стабильностью несколько частей на \(10\space ^{11}\) на временном промежутке от секунд до часов.
==451
Когда речь заходит о таких цифрах, и температура перестаёт быть возмущающим фактором, на первых план выходят эффекты «старения» ( со временем частота кристалла непрерывно увеличивается ), стабильности питания и внешних воздействий - ударов и вибрации, которые, к слову, являются самой сложной проблемой для кристаллов наручных часов. Представление о процессе старения даёт спецификация 1000B, которая оговаривает изменение частоты на уровне \(1:10\space ^{10}\) max в день после первого месяца работы. Старение происходит из-за постепенного снятия внутренних напряжений и для высококачественных кристаллов успокаивается после нескольких месяцев работы 51 .
Термостатированные генераторы могут быть весьма миниатюрными, если того требуют условия эксплуатации. Valpey Fisher напыляет резистивный нагреватель прямо на кварцевый кристалл. В итоге их OCXO имеет объём ∼1.3cm³ и требует для нагревателя только 0.15W .
7.1.7.B Атомные стандарты
Атомные стандарты частоты применяют там, где недостаточно термостатированных кристаллов. В них используется факт поглощения микроволнового излучения парами рубидия ( Rb) на длине волны атома или переходы между атомными уровнями цезия ( Cs ) в качестве опорной частоты для кварцевого генератора. Коммерческие стандарты частоты достигают точности и стабильности от \(1:10\space ^{11}\) для рубидиевых и до \(1:10\space ^{13}\) у цезиевых. Цезиевый стандарт частоты является официальным эталоном времени в США и хранится в Национальном Институте Стандартов и Технологии ( NIST ) и Морской Обсерватории .
Ещё одним очень стабильным эталоном является атом водорода. В отличие от Rb и Cs, здесь резонатором, а не пассивным опорным сигналом, служит сам атом. Его стабильность несколько частей на \(10\space ^{14}\) . Последние исследования концентрируются вокруг «охлаждаемых» ионных и атомных ловушек, сулящих более высокие результаты. Эти же принципы позволяют создать оптические стандарты, которые затем связываются с радиочастотным опорным сигналом с помощью «оптической гребёнки» (optical comb). Физики полагают, что в этом направлении достижимы цифры порядка единиц на \(10\space ^{17}...10\space ^{18}\) .
И, наконец, совсем не обязательно тратить кучу денег на рубидиевый стандарт. Вместо этого можно синхронизировать точный генератор с сигналом 1 pps , получаемым с навигационной системы GPS 52 . Группировка из 24 спутников, движущихся по 12-часовым орбитам, закрывают всю поверхность земли, кроме полярных областей и изначально созданы для решения задач точного позиционирования и службы времени. Спутники несут на борту точные атомные часы и передают «навигационные сообщения» , используя сложную двухчастотную посылку ( 1.575 и 1.228 GHz ) с размытым спектром. Приёмник GPS может рассчитать своё положение по сигналам четырёх спутников [* по трём - положение, по четырём - положение и высоту] и получить время. Недорогие приёмники доступны как в виде отдельного устройства, так и в составе современных смартфонов и т.п. оборудования и исходно предназначены для выяснения положения, поэтому они не восстанавливают опорную частоту. Но, если потратиться на лабораторный вариант, например, Symmetricom 58503B «GPS Time and Frequency Reference Receiver», то можно разжиться генератором 10 MHz со стабильностью \(1:10\space ^{12}\) ( с усреднением за 1 день ) и источником импульсов 1 pps с джиттером 20 ns . Стоит это удовольствие $4500 и требует для работы внешней антенны.
В табл. 7.2 собраны различные методы построения генераторов частоты и их характеристики.
7.1.8 Синтез частоты: DDS и PLL
Опорная частота стабильна , т.е. её нельзя подстроить. Существуют два красивых метода, которые позволяют получить сигнал нужной частоты, который будет иметь такую же стабильность, как опорный. Речь идёт о прямом цифровом синтезе ( DDS ) и фазовой автоподстройке частоты ( PLL ). PLL относится к технике смешанных сигналов и подробно рассматривается в Части 13 . Но оба метода тесно увязаны с темой генераторов частоты, поэтому будут рассмотрены здесь на базовом уровне.
7.1.8.A Прямой цифровой синтез
Основная идея состоит в заполнении блока памяти цифровыми значениями синуса [* или любой другой периодической функции ] для равноотстоящих аргументов ( например, для шага 1° ). Теперь становится возможной генерация быстрого синусоидального [* или ещё какого] сигнала за счёт перебора последовательных адресов и отправки данных из памяти в цифро-аналоговый преобразователь (ЦАП ).
==452
Схематично процесс показан на рис. 7.42A , а чуть более сложный способ, применяемый на практике, приведён на рис. 7.42B . В первом случае n-разрядный адрес для ячеек памяти, содержащих значения функции с точностью k разрядов, формирует простой двоичный счётчик ( n разрядов означает, что на один цикл 360° приходится 2n шагов ). Во втором - этим занимается регистр фазы, который дополнительно учитывает значение слова подстройки частоты ( FTW ). С каждым тактом фаза [* адрес памяти ] увеличивается на \(Δ φ\)=(360°/2n)·FTW [* это выражение для фазы, выраженной в градусах, а, если мерить её в частях целого ( а именно в такой форме она используется во всех формулах ), то \(Δ φ\)=(1/2n)·FTW ] . Т.е. в каждом цикле тактовой частоты текущее значение фазы изменяется на величину FTW [* другими словами, FTW - множитель тактовой частоты] . Выходная частота равна \( f_{out}\)= [*\(f_{clk}·Δφ\)] =\(f_{clk}\) (FTW/2n) .
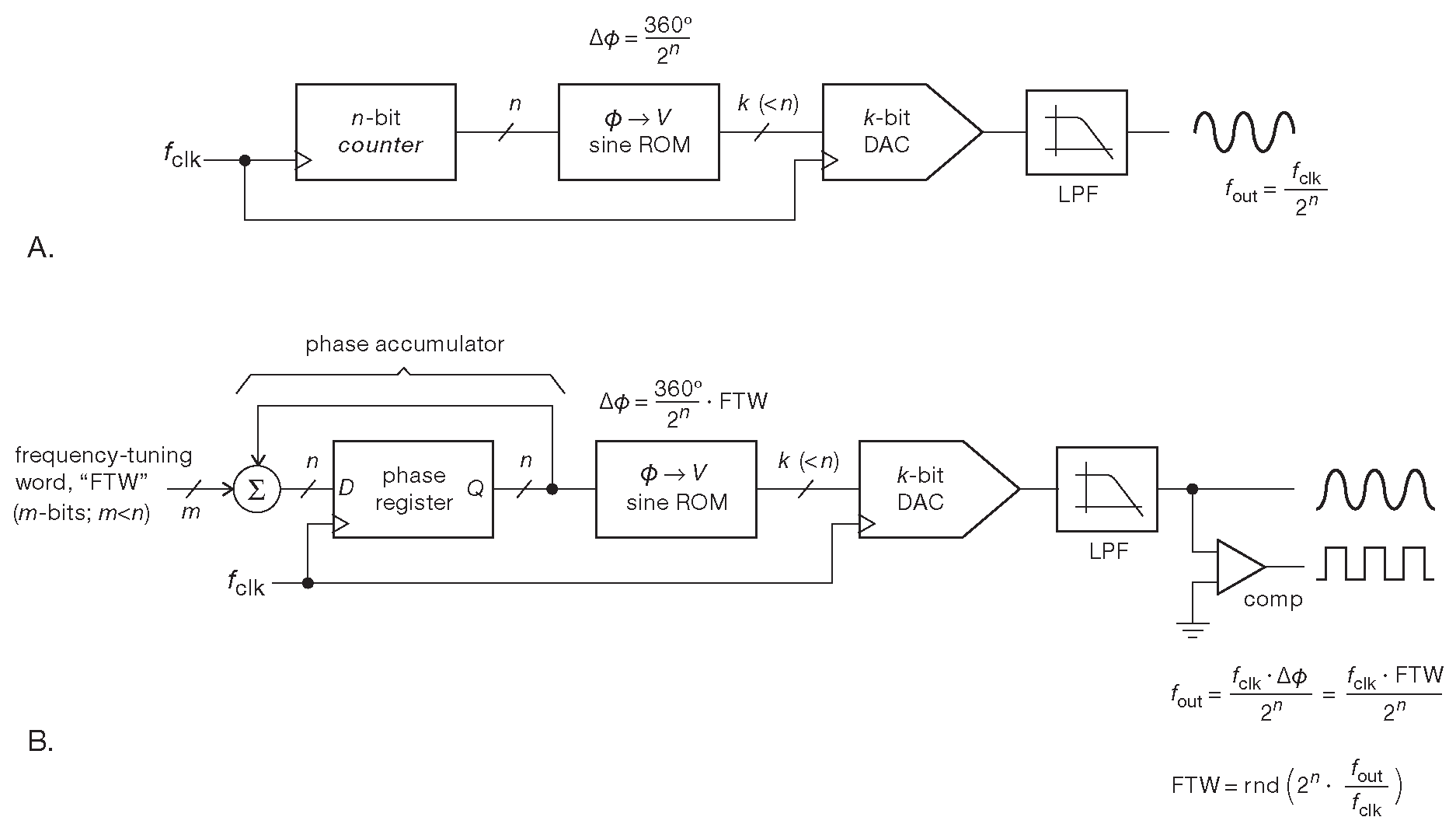
Рис.7.42 Прямой цифровой синтез позволяет получить выходной сигнал, параметры которого хранятся в ПЗУ. В простейшей конфигурации (A) последовательно увеличивающийся счётчик задаёт адрес ПЗУ. Более практичная схема (B) содержит аккумулятор фазы , позволяющий повысить разрешение по частоте [* Правильная формула \(f_{out}=f_{clk}·Δφ=f_{clk}·FTW/2^n\). Операция «rnd» означает округление до ближайшего целого ]
У данного метода есть некоторые недостатки. Реальный выходной сигнал имеет ступенчатую форму, т.к. получается из набора дискретных значений напряжения, соответствующих таблице в памяти. Его можно, естественно, сгладить фильтром нижних частот, но, поступая так, вы лишаетесь возможности менять частоту в широких пределах, т.к. фильтр надо выбирать, чтобы он пропускал только основной [* синтезируемый] сигнал и давил тактовую частоту. Та же проблема наблюдается и в резонаторе на переключаемом конденсаторе ( §7.1.9.B ). Можно уменьшить величину шага, но это уменьшает максимальную выходную частоту.
Современные микросхемы DDS имеют в своём составе таблицу значений синуса, ЦАП и вообще всё, что может понадобиться для получения выходного сигнала, исключая источник стабильной тактовой частоты ( в качестве такового чаще всего выступает обычный кварцевый генератор, см. §7.1.6 ). Эти компоненты недороги и работают на удивление быстро. Например, серия AD9850 включает AD9852, который способен выдавать на выходе 150 MHz , имея разрешение по частоте 48 разрядов ( т.е. с точностью до микрогерц ). Стоит $15 в количествах. Если хочется погорячее, то к вашим услугам AD9912 ( $37 ) с тактовой частотой 1 GHz ( \( f_{out}\space (max)\)=400 MHz ) и 14-разрядным выходным ЦАПом. DDS синтезаторы позволяют задавать качание частоты - линейный рост частоты выходного сигнала со временем, а также амплитудную, частотную и фазовую модуляцию ( изменение параметра под внешним воздействием ). AD9852 способен переварить поток команд на изменение частоты с интенсивностью 100 миллионов команд в секунду, т.е. позволяет получить перестраиваемый генератор .
Другие члены семейства позволяют синхронизировать фазу или задать для неё очень точный сдвиг, т.е. получить точный квадратурный ( sine + cosine ) генератор с ошеломляющими параметрами с помощью нескольких дополнительных микросхем ценой несколько долларов в сумме.
7.1.8.B Фазовая автоподстройка частоты
Это способ получения сигнала с частотой, которая точно соотносится с входным опорным сигналом в соотношении, выражаемом рациональной дробью \( f_{out}=f_{osc}\)×(n/r) , где r и n - целые числа. Данную схему можно рассматривать как обобщённый вариант делителя частоты. Фазовая автоподстройка являет собой смесь аналоговых и цифровых методов преобразования сигналов, поэтому подробное описание откладывается до §13.13 .
Сейчас важно лишь то, что эта техника даёт очень широкие возможности по созданию периодических сигналов. Например, если взять в качестве опорного источника кварцевый генератор на 16 MHz и установить делитель r=16 , то на выходе схемы PLL будет частота n×1 MHz . Т.е. получаем генератор, частота которого перестраивается с шагом 1 MHz и типовым рабочим диапазоном 25..500 MHz . Фазовая автоподстройка активно используется в связной технике, радарах, телевидении и т.п.
Table 7.2 Oscillator Types®
Notes: (a) somewhat subjective evaluations. (b) tuning via operating current. (c) cylindrical cavity, waveguide, or dielectric "pill" resonator. (d) tuning via mechanical plunger, varactor, or YIG. (e) from 8.634488275 GHz resonance. ( f) long-term. ( g ) from 9.192631770 GHz resonance. (h) from 1.420405751767 GHz oscillation. (k ) long-term.==453
Из примера понятно, что достаточно сложная техника синтеза сигналов доступна в виде удобных микросхем. Кто-то другой уже позаботился о выборе фазового детектора, о генераторе, управляемом напряжением, и об устойчивости петли обратной связи. Кроме того, есть недорогие законченные кварцевые модули ( §7.1.6.F ), содержащие кристалл, генератор и PLL и позволяющие задавать нужную частоту. Их выпускают Epson ( серия SG8002 ), ECS ( серия ECS-), Citizen ( серия CSX-750P ), CTS ( серия CP7 ) и Cardinal ( серия CPP ). Упаковываются такие устройства в корпуса для выводного ( DIP ) и поверхностного монтажа.
7.1.9 Квадратурные генераторы
Бывает, что требуется пара сигналов одинаковой амплитуды с разницей фаз 90° . Такие сигналы можно рассматривать как синусный и косинусный ( или I и Q от «in-phase» и «quadrature» ). Такая пара называется «квадратурной». Одно из важных приложений - телекоммуникационная сфера ( квадратурные смесители, передача на одной боковой полосе ). Квадратурная пара позволяет получить сигнал любой фазы, о чём пойдёт речь ниже.
Первое, что приходит в голову, возможность довернуть синусоидальный сигнал на 90° , пропустив его через интегратор или дифференциатор. Получим правильный сдвиг фазы, но некорректную амплитуду ( объясните почему ). Ниже приводятся несколько рабочих способов.
7.1.9.A Парные интеграторы
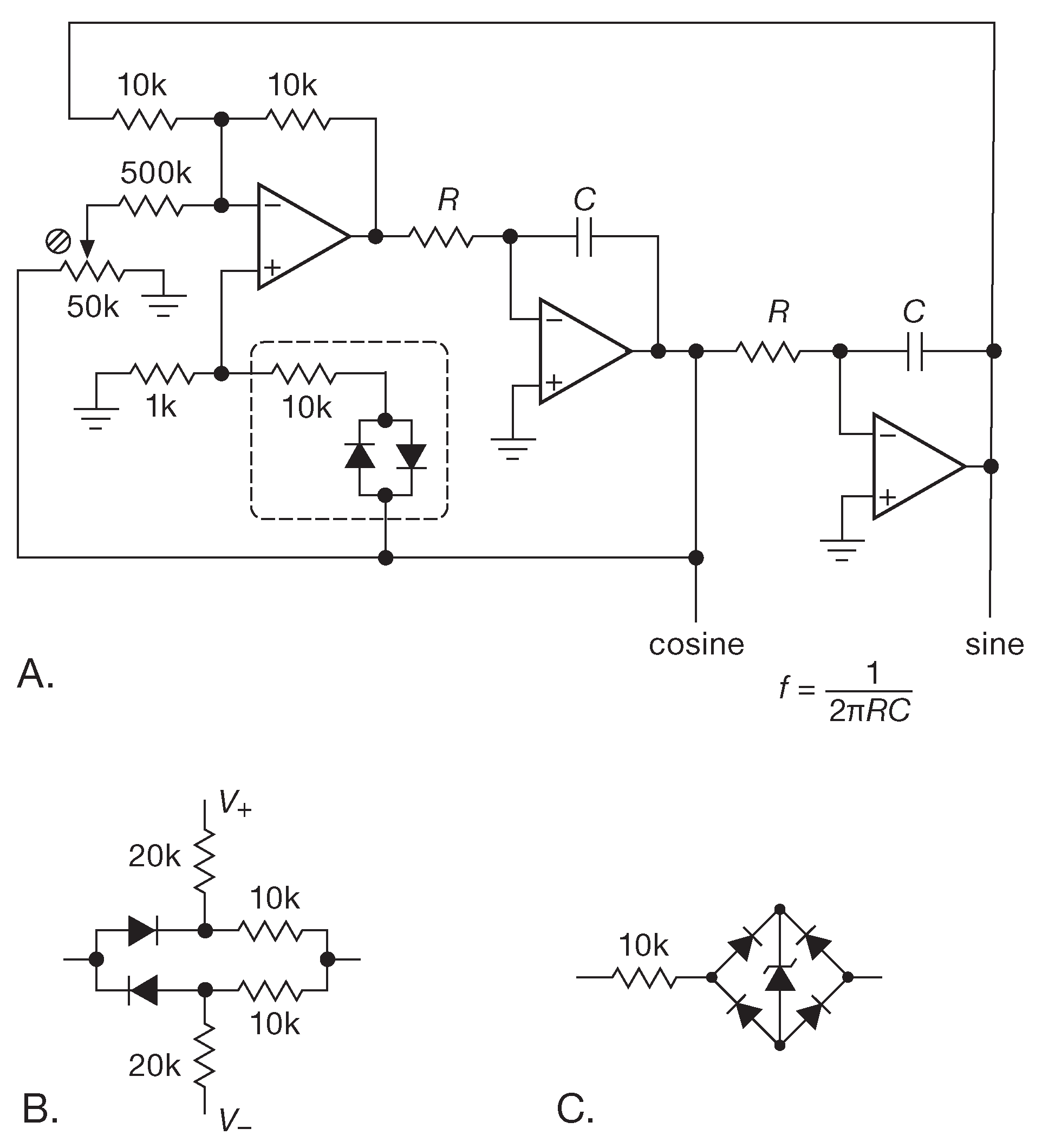
Рис.7.43 Квадратурный генератор синусоидального сигнала ( модифицированная схема Тони Вильямса ). (A) Базовая схема с диодным ограничителем ( пунктирная область ). (B) Диодный ограничитель с заданием рабочей точки. (C) Ограничитель на стабилитроне
На рис. 7.43 приведён вариант схемы, используемый уже несколько десятилетий. В ней используются два последовательных интегратора ( –90° каждый ) в цепи обратной связи усилителя с единичным коэффициентом ( всего 180° ). Генерация возникает на частоте, на которой интеграторы имеют единичное усиление. В этой точке реактивное сопротивление ёмкости \(1/( 2πfC ) \) равно \(R\) . Диоды ограничивают амплитуду сигнала ∼300 mV . Схема была проверена с LMC6482 при питании ±5V , \(R\)=15.8 kΩ и \( C \)=10 nF ( \( f_{osc} \)=1 kHz ). Выходной сигнал показан на рис. 7.44 . Результаты измерений: частота 997 Hz , искажения 0.006% и 0.02% для синуса и косинуса соответственно.
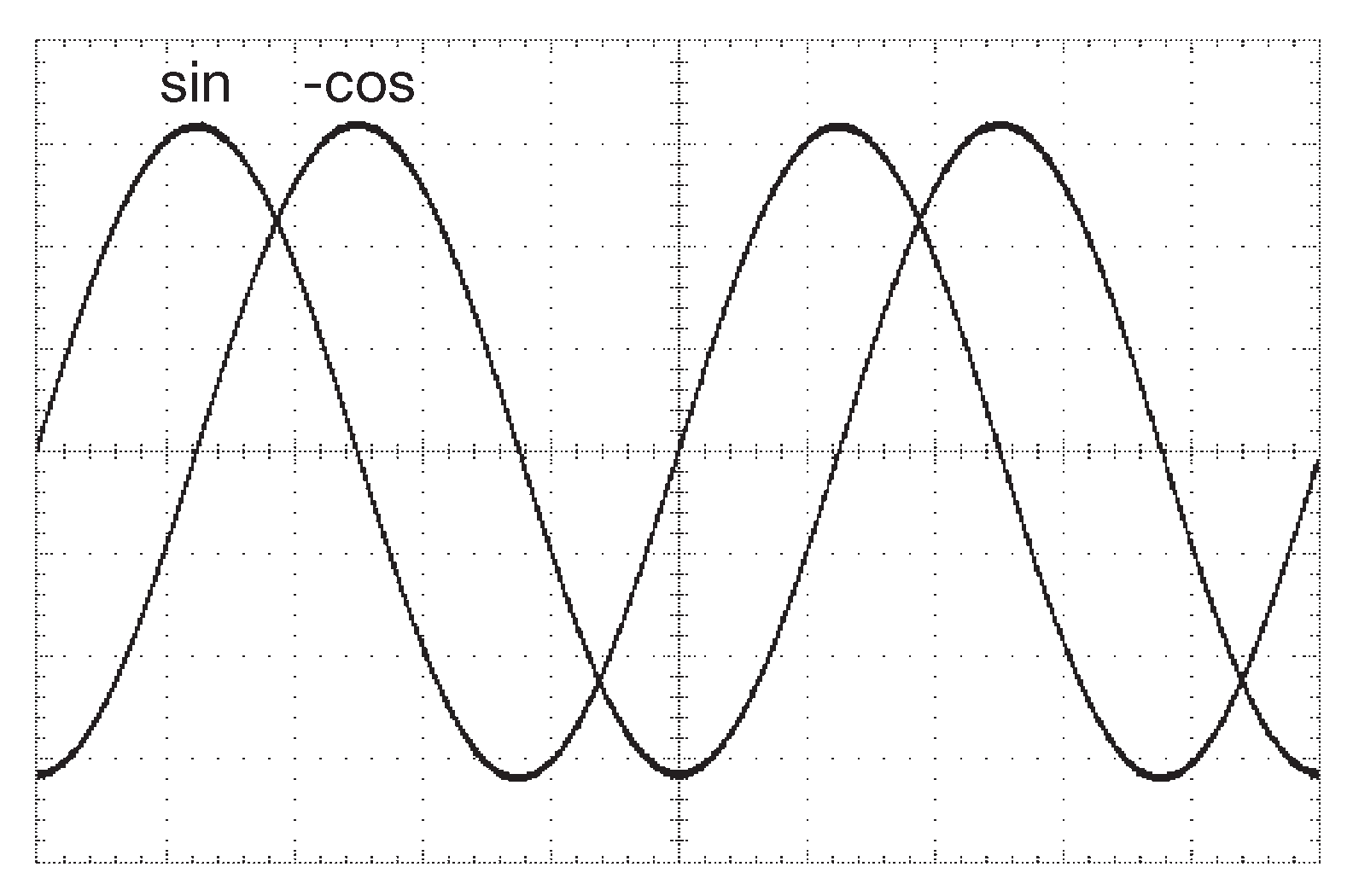
Рис.7.44 Выходной сигнал схемы 7.43A . По горизонтали 200 μs/div , по вертикали 100 mV/div
==454
Простой диодный ограничитель не обеспечивает точный контроль амплитуды и, к тому же, ограничивает её величиной ∼300 mV . Более удачный вариант показан на рис. 7.43B . Здесь границу задают делители, а диоды переходят в проводящее состояние, когда сигнал выходит за неё. С указанными номиналами измерения дают амплитуду 3.3 V . На рис. 7.43C показан третий вариант ограничителя, который предпочитают некоторые разработчики. Стабилитрон, включённый в диагональ моста, работает двухсторонним ограничителем. Для больших сигналов ( 5V и выше ) хорошо работают обычные стабилитроны, но низковольтные модели имеют слишком «мягкую» переходную характеристику ( см. рис. 1.17 ), поэтому на их место лучше поставить 2-выводной опорный источник, который гораздо больше походит на идеальный стабилитрон. В качестве примера можно назвать LM385-1.2 и -2.5 ( 1.24 V и 2.50 V ), AD1580 ( 1.22 V ) и ADR510 ( 1.0 V ). Схема только выиграет, если параллельно стабилитрону или опорному источнику поставить конденсатор, который будет поддерживать на ограничителе напряжение в момент перехода сигнала через ноль.
7.1.9.B Резонатор на переключаемом конденсаторе
Очень красивый приём. Рис. 7.45 показывает, как собрать из фильтра на переключаемом конденсаторе генератор квадратурных сигналов с самовозбуждением. Понять, как работает схема, проще всего, предположив, что синусоидальный сигнал на выходе уже есть. ОУ \(U_{2a}\) , включённый компаратором, превращает выходной синус в меандр с уровнем ±5V , который возвращается на вход фильтра. Последний включён как узкий полосовой фильтр ( Q=10 ), превращающий меандр обратно в синус, поддерживая тем самым генерацию. Цифровой тактирующий вход «CLK» задаёт центральную частоту полосового фильтра, а значит, и частоту генерации ( здесь \( f_{clk} \) /100 ). Схема выдаёт квадратурную пару с одинаковыми амплитудами и способна создавать сигнал частотой от нескольких герц до более чем 10 kHz . Отметим, что выход является лишь ступенчатым приближением к желаемому синусоидальному сигналу. За ступенчатость несёт ответственность фильтр на переключаемом конденсаторе [* фильтр «дискретного времени»] , см. рис. 7.46 . [* Чтобы уменьшить ступеньку надо брать фильтр с большим отношением \( f_{clk}:f_{out}\) , см. §6.3.6.D ] .
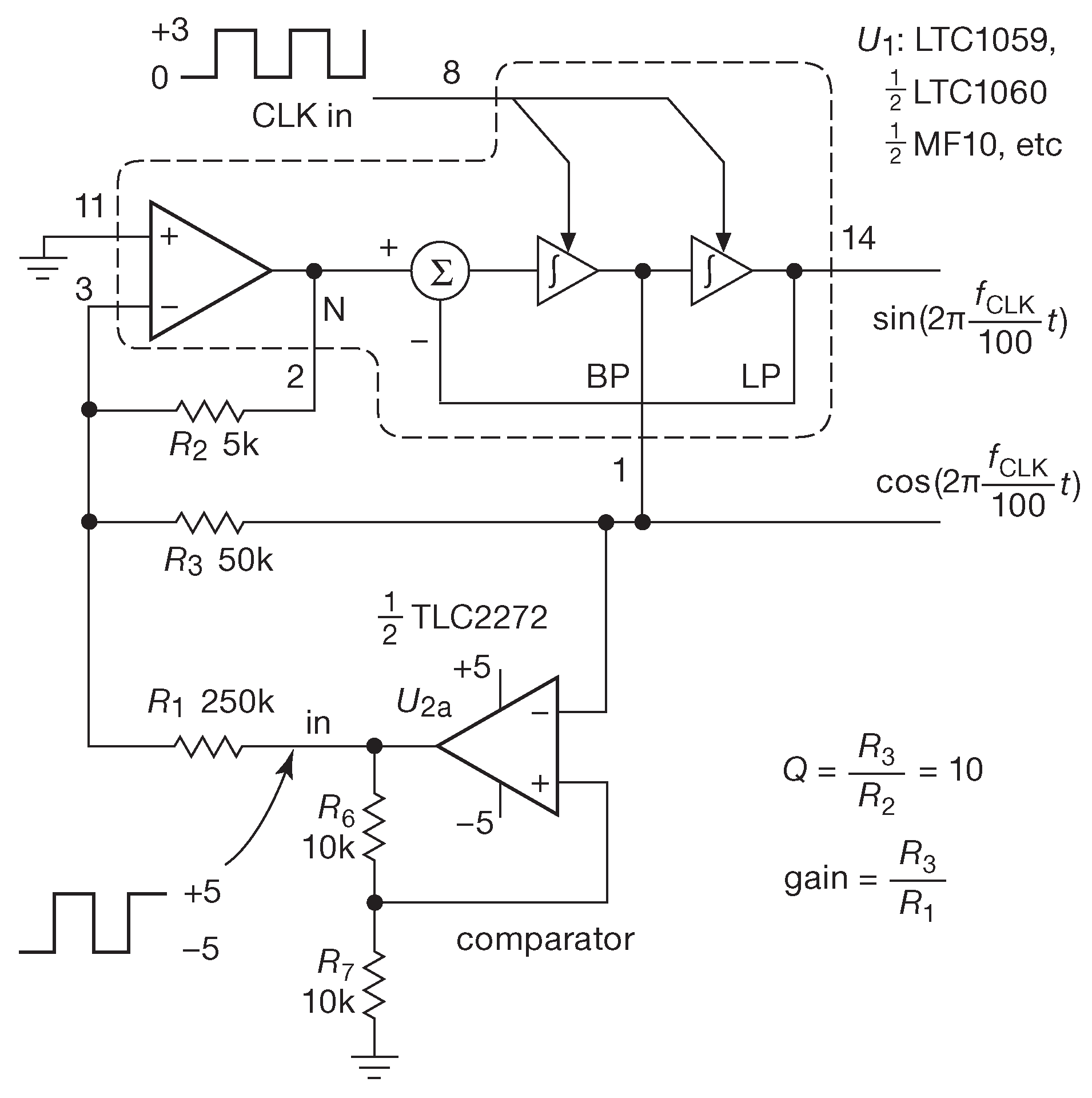
Рис.7.45 Синусоидальную квадратурную пару можно получить, охватив компаратор обратной связью с узкополосным фильтром на переключаемом конденсаторе
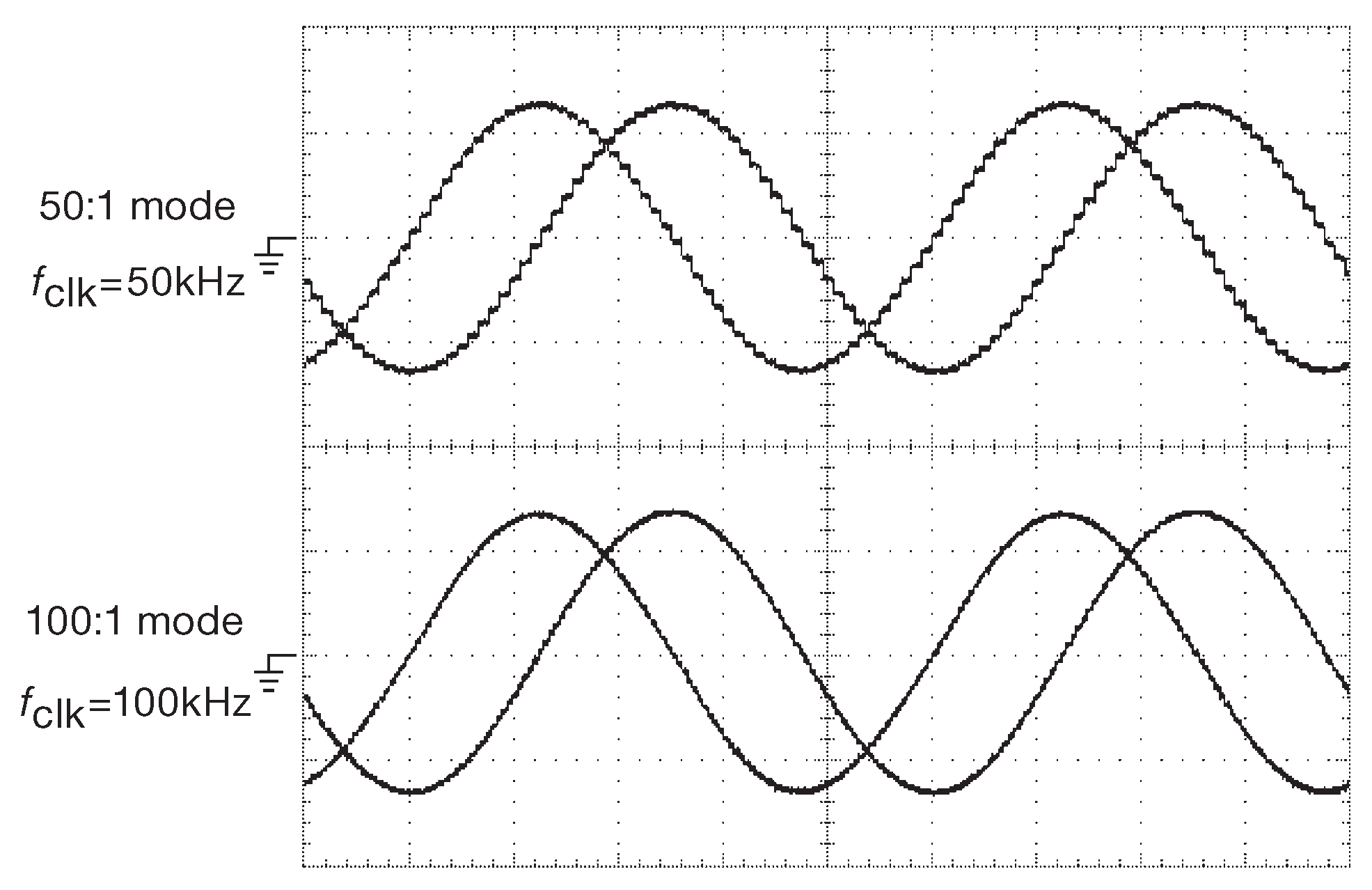
Рис.7.46 Выходной сигнал схемы 7.45 . Фильтр на переключаемом конденсаторе создаёт ступенчатое приближение к идеальному синусоидальному сигналу. Ступенчатость становится заметнее, если взять более грубый фильтр с отношением \( f_{clk}:f_{out}\)=50:1 . Кстати, схема знает значение π . Выходная амплитуда равна 4/π вольт. По горизонтали 200 μs/div , по вертикали 1 V/div
==455
У схемы есть интересная особенность - способность «вычислять π». Если установить усиление фильтра \(R_3/R_1\)=0.2 и подать на вход точный меандр ±5V , то можно ожидать на выходе сигнал с уровнями ±1V . Однако фильтр пропускает на выход только основную частоту, амплитуда которой 4/\(π\) от входного меандра. Таким образом, на выходе будет (4/\(π\))×5×0.2 = 4/\(π\) ≈ 1.27 V , что можно видеть на картинке с осциллографа ( рис. 7.46 ).
7.1.9.C Прямой цифровой синтез
Этот метод уже упоминался ( §7.1.8 ) в качестве основного для получения синусоидальных сигналов ( и вообще сигналов любой желаемой формы ) с частотой, находящейся в точно заданной пропорции с входным опорным генератором. Помимо прочих достоинств, данный метод позволяет создавать квадратурные сигналы ( или сигналы с любым заданным соотношением фаз ). На рис. 7.47 показана микросхема фирмы Analog Devices, которая изначально предназначена для формирования квадратурных синусоидальных сигналов. Она позволяет задавать выходную частоту с точностью до микрогерц и имеет массу очень удобных дополнительных возможностей: цифровые смесители ( для амплитудной модуляции ), таймеры и аккумуляторы ( для частотной и фазовой модуляции ). Справочные данные рекомендуются к ознакомлению.
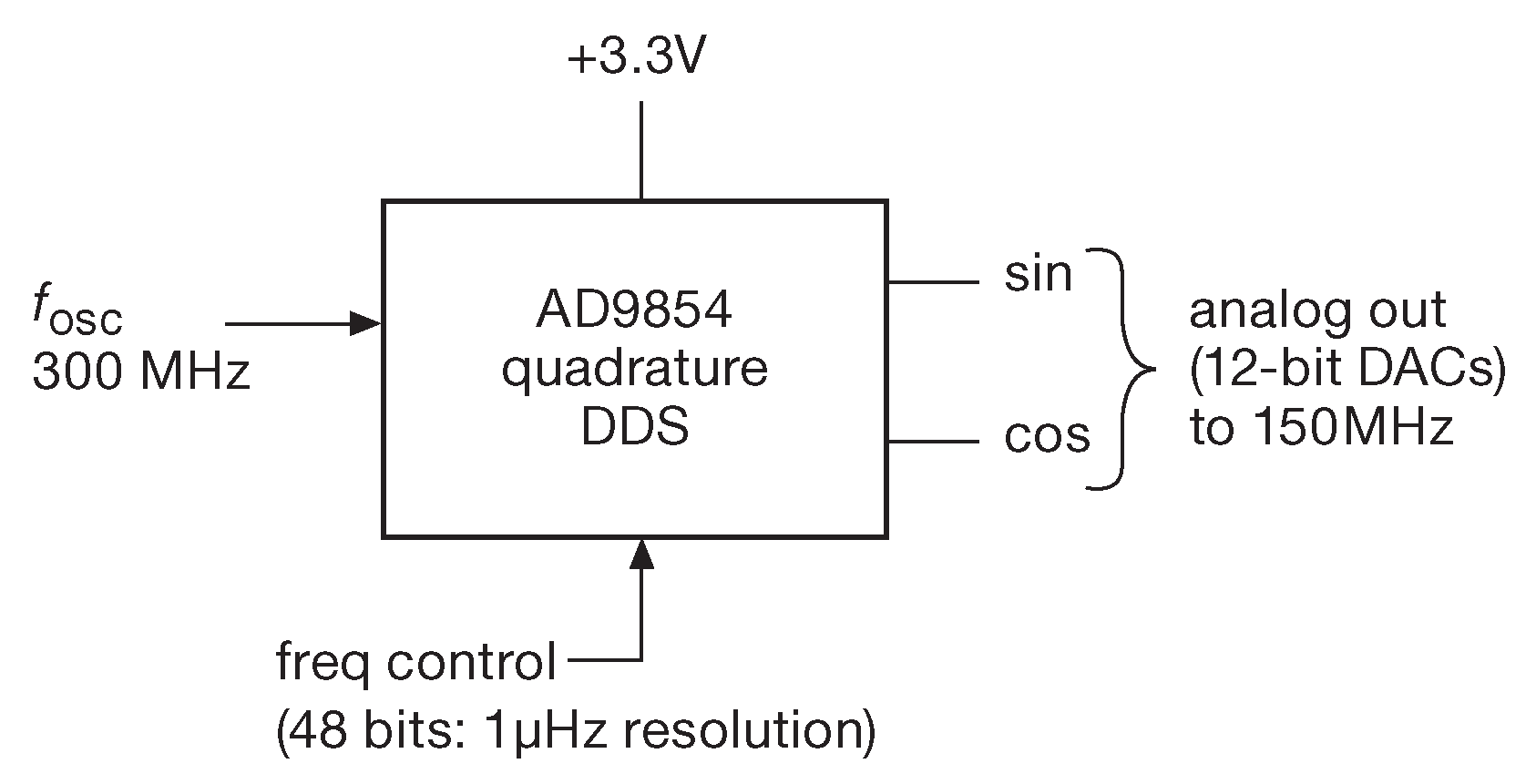
Рис.7.47 Создание квадратурных сигналов с помощью DDS. У AD9854 под крышкой есть много интересных штук ( см. текст )
7.1.9.D Фильтр симметричных составляющих
Существует очень забористый вариант RC фильтра, обладающий способностью превращать входное синусоидальное напряжение в два синусоидальных сигнала, разница фаз между которыми примерно равна 90° . Радиолюбители используют этот метод под названием «фазирование» при связи с одной боковой полосой. При радиопередаче на вход подают речевой сигнал. К сожалению, работает такой подход только в узком диапазоне частот и требует элементов с точно заданными номиналами.
Более высокие результаты показывает фильтр симметричных составляющих - цепь , образованная повторяющимися фрагментами из резисторов одного номинала и конденсаторов с уменьшающимися в геометрической прогрессии емкостями, см. рис. 7.48 . На вход такой RC матрицы подаются два противофазных сигнала ( это несложная задача, всё, что требуется, - инвертор с единичным усилением ). На выходе - четыре квадратурных сигнала. 6-стадийный вариант позволяет достичь ошибки ±0.7° в диапазоне частот 40:1 . 8 секций расширяют его до 150:1 . На рис. 7.49 приведены результаты моделирования 8-стадийной матрицы в SPICE. Схема имеет неплохие параметры от 400 Hz до 50 kHz .
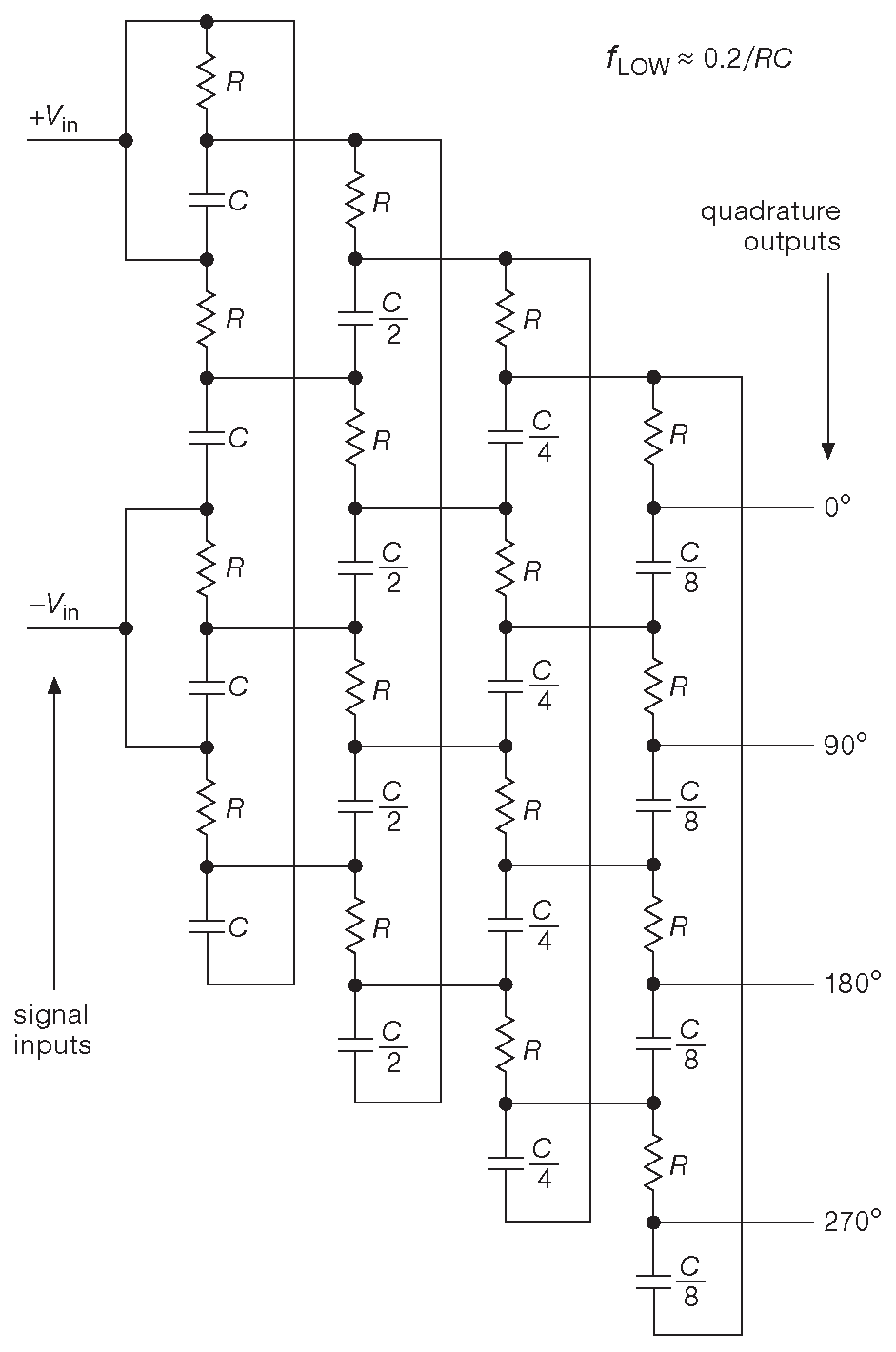
Рис.7.48 4-стадийная фильтр симметричных составляющих. Рабочий диапазон схемы начинается с частоты \( f_{low}\)≈0.2/\((RC) \) , а верхняя граница соотносится с нижней в той же пропорции, что и отношение емкостей входной секции к емкостям выходной \( f_{high}\space /f_{low}≈ C_{in}/C_{out}\)
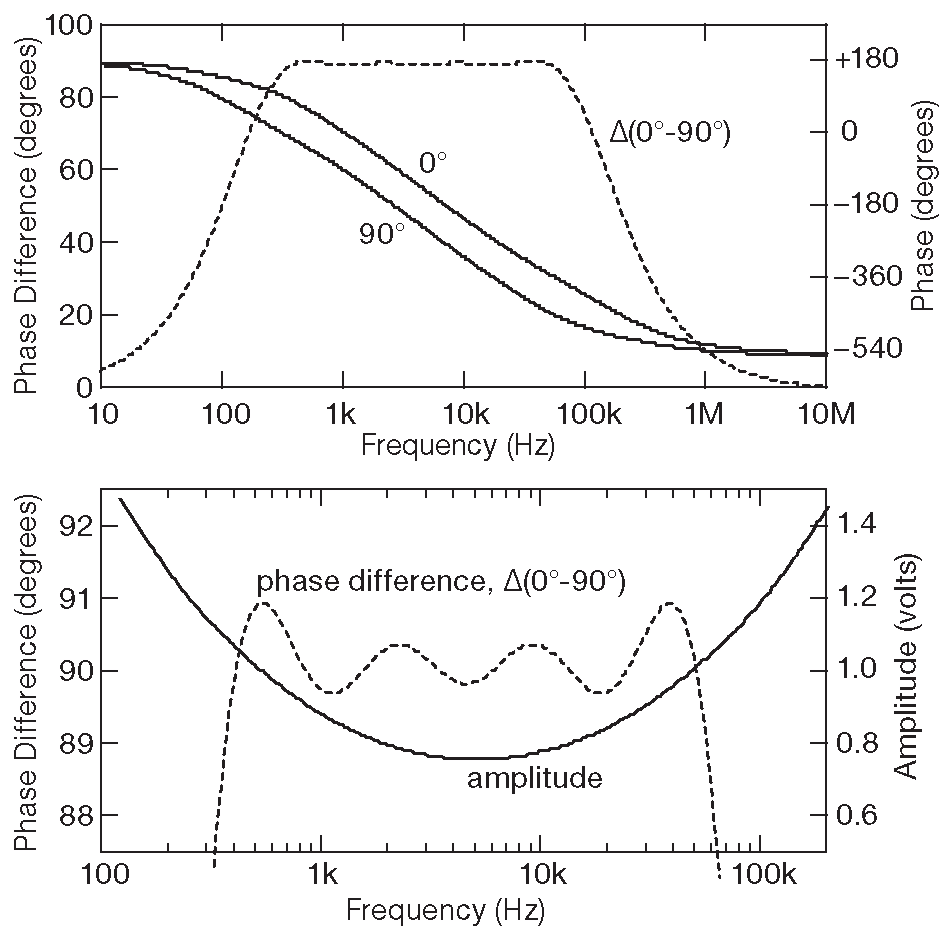
Рис.7.49 Результаты моделирования в SPICE параметров фазы и амплитуды 8-стадийного фильтра симметричных составляющих ( \(R\)=10 kΩ , \( C \)=40 nF ). На нижнем графике участок точного выполнения квадратурных соотношений увеличен. Отметим, что в квадратурной паре речь идёт о разнице фаз
7.1.9.E Квадратурные прямоугольные сигналы
Когда речь идёт о прямоугольных сигналах, создавать квадратурные пары проще простого. Основная идея: получить удвоенную, относительно требуемой, частоту и поделить её по степеням двойки цепочкой триггеров ( рис. 7.50 ). Схема выдаёт идеальный результат от постоянного тока и как минимум до 100 MHz .
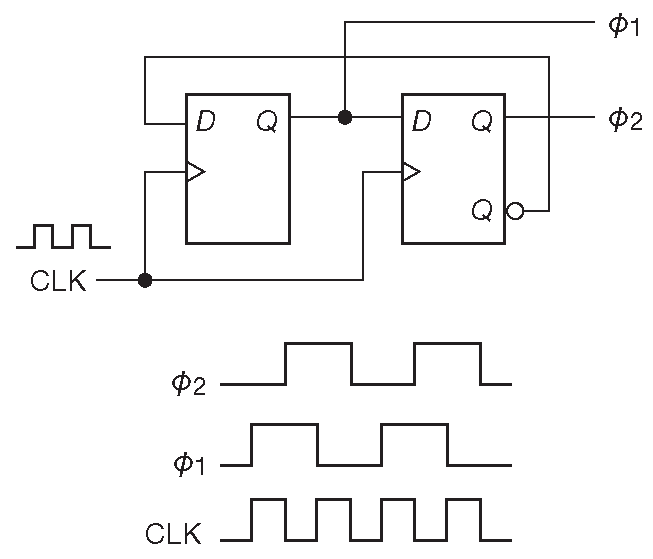
Рис.7.50 Квадратурные цифровые сигналы, полученные с помощью универсальных D-триггеров
7.1.9.F Квадратурные сигналы на радиочастотах
==456
На радиочастотах ( до нескольких мегагерц квадратурные синусоидальные сигналы легко получить с помощью специального гибридного устройства . В низкочастотной части электромагнитного спектра ( от нескольких мегагерц до 1 GHz ) такое устройство делают на основе мотанного сигнального трансформатора. На более высокой частоте ту же схему выполняют по микрополосковым технологиям ( на отрезках фольги, изолированных от экранирующего земляного слоя, см. Часть X1 [* §X1.1 , ( §X1.1.4.C ) ] ) или на волноводах ( полых металлических трубах прямоугольного сечения ). Все эти методы имеют узкую рабочую полосу, которая редко превышает октаву ( т.е. отношение частот 2:1 ).
7.1.9.G Получение синусоидального сигнала с заданной фазой
Из квадратурной пары легко получить сигнал с любой фазой. Для этого надо просто сложить фазный (I) и квадратурный (Q) сигнал через резистивный делитель, а выход брать со средней точки. Проще всего использовать потенциометр, включённый между «I» и «Q». При вращении ручки потенциометра фаза сигнала на его движке будет плавно меняться от 0° до 90° . Результирующая фаза полностью независима от частоты, но, к сожалению, влияет на амплитуду. Наименьшее значение –3dB сигнал имеет при фазе 45° . Расширить диапазон фазировки можно, используя инверсию основной пары «I» и «Q» с помощью усилителя с \( G_V\)=–1 .
==457
Способность создавать пачки синусоидальных сигналов с заданной фазой и амплитудой чрезвычайно важна в цифровых системах связи. Метод называется «квадратурная амплитудная модуляция» ( QAM , произносится «quahm» ). Каждая порция по нескольку бит информационной посылки превращается в QAM «символ», передаваемый по каналу связи. Например, в большинстве стандартов кабельного телевидения используется кодировка 256-QAM. Каждый символ 256-QAM ( один из 256 ) несёт в себе 8 бит исходной информационной посылки и представляет собой небольшой кусочек синусоиды, всего несколько периодов, имеющий точное значение фазы и амплитуды, которые однозначно этот символ определяют 53 . [* Методы детектирования см. §13.13.6.E ]
С помощью DDS выходную фазу относительно синхронизирующего импульса или другого DDS синтезатора задавать ещё проще, потому что микросхема позволяет добавлять задаваемое пользователем смещение к внутреннему аккумулятору фазы. Например, AD9951 имеет 14-разрядное слово сдвига фазы , позволяя менять фазу с шагом 360°/214 или 0.02° . Величину смещения можно менять «на лету», реализуя тем самым фазовую модуляцию.
7.1.10 «Джиттер» в генераторах
В дополнение к обычным параметрам - частоте, амплитуде и форме выходного сигнала у каждого генератора есть ещё стабильность . Если выходной сигнал «плывёт» по времени, температуре или питающему напряжению, можно говорить о стабильности параметров ( или отсутствии таковой ) и вводить соответствующие коэффициенты. Например, кварцевый кристалл может иметь температурный коэффициент 1 ppm/°C и подходить ( или не подходить ) для решения задач во времязадающих устройствах, аппаратуре связи и т.п.
Но названные категории не исчерпывают список параметров. Например, можно иметь генератор, усреднённая частота которого в точности равна 10.0 MHz и не зависит от температуры и времени, но имеет вариации во времени пересечения нулевого уровня от цикла к циклу. Данное явление можно рассматривать как нестабильность на коротком временнОм интервале, в противоположность стабильности на длинном интервале, по которой определяются временнЫе и температурные коэффициенты 54 . Описанное неприятное свойство имеет множество имён, зависящих от контекста. Если речь идёт о синусоидальном сигнале в приложении к системам связи, то говорят о фазовом шуме или спектральной чистоте . Если же обсуждаются цифровые сигналы, задачи оцифровки и синтеза частоты или тактирование импульсных последовательностей, то речь идёт о джиттере .
Ещё несколько замечаний о джиттере. ВременнОй джиттер возникает, когда активный перепад на выходе появляется в результате пересечения задающим периодическим сигналом некоторого граничного уровня. Речь может идти о релаксационном RC контуре или о кварцевом генераторе. Ситуация разрисована на рис. 7.51 . Сигнал с конечной скоростью нарастания S ( вольт в секунду ) пересекает пороговый уровень, причём оба напряжения - и сигнал, и порог не идеальны: каждый содержит дополнительный шум \(v_n\) . Назовём дополнительный шум \(v_n( sig ) \) и \(v_n( th ) \) . Таким образом, имеется и некоторая временнАя неопределённость: момент пересечения зашумлённым сигналом зашумлённого же порогового уровня может меняться ( и изменится ) на величину: \[ Δ t=\frac{Σ v_n}{slew\text_rate}=\frac{v_n( sig )+v_n( th)}{S} \]
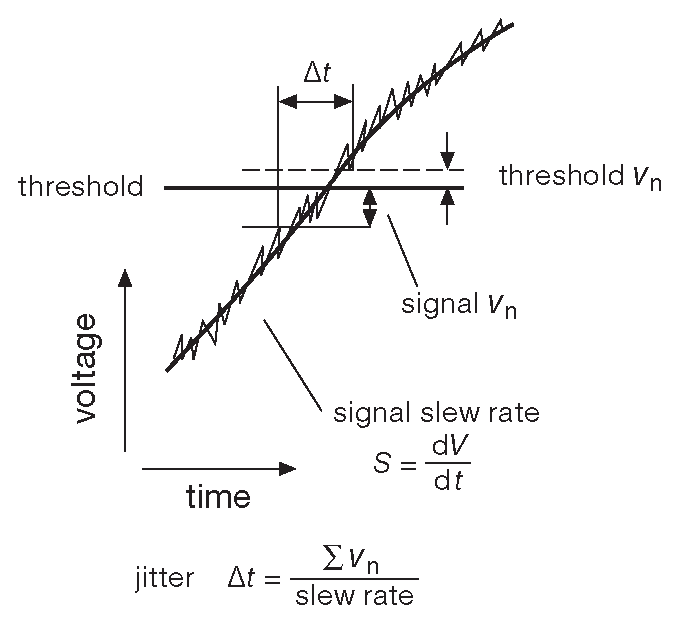
Рис.7.51 Схема возникновения джиттера: сигнал с конечной скоростью нарастания пересекает пороговый уровень
У медленных сигналов при заданном уровне шума сигнала и порога джиттер больше. Синусоидальный сигнал с частотой \( f \) и максимальной скоростью нарастания \( S=2πfV_o\) , где \( V_o\) - пиковая амплитуда сигнала ( т.е., если пороговый уровень отстоит от средней точки, то скорость нарастания ниже ). Скорость нарастания импульсного сигнала или перепада можно принять за \( S=V_{step}\space /t_r\) , где \( t_r\) - время нарастания ( или в общем случае, время перехода между состояниями ).
Стабильность и джиттер генераторов - очень важные характеристики. Они будут обсуждаться подробно в Части 13 в приложении к аналого-цифровым преобразованиям, фазовой автоподстройке частоты [* §13.13.7 ] и последовательным каналам связи [* это Часть 12 см. разбор «межсимвольной интерференции» на стр. 870 ] .
==457
51 Паспортные данные на 1000B сообщают, но не гарантируют, что хорошо состаренные экземпляры уходят не более чем на одну часть на \(10\space ^{11}\) в день. <-
52 Есть ещё две аналогичные навигационные системы: русская ГЛОНАСС и европейская Galileo. Последнюю обещают запустить в коммерческую эксплуатацию в 2020 году. <-
53 Набор амплитуд и фаз, определяющий канальный QAM символ, выбирается, исходя из минимальной ошибки при заданных параметрах кабеля. <-
54 Специалисты, занимающиеся стабильностью генераторов и находящие отраду в злоключениях несчастных приборов, делают очень сложные измерения этой самой стабильности. В частности дисперсию Аллана , которая даёт график стабильности генератора по усреднённому времени. <-

