1.2 (II) Напряжение, ток и сопротивление
==8
1.2.4 Источники напряжения и тока
Идеальный источник напряжения - двухвыводной «чёрный ящик», который сохраняет заданное напряжение между своими выводами, независимо от величины сопротивления нагрузки. Это в частности означает, что источник напряжения должен выдавать ток \(I=V/R\) , когда между его терминалами помещается сопротивление \(R\) . Настоящие источники напряжения ограничивают отдаваемый ток некоторым максимальным значением и больше всего напоминают идеальный источник с некоторым последовательным сопротивлением. Очевидно, что чем меньше величина последовательного сопротивления, тем лучше. Например, обычная щелочная батарея «9V» выглядит как идеальный источник напряжения с последовательным резистором 3 Ω . В состоянии короткого замыкания такая батарея даёт 3A ( такой ток убьёт её за несколько минут ). Источники напряжения «любят» разомкнутые цепи и «ненавидят» короткозамкнутые. Термины «разомкнутая» и «короткозамкнутая» цепь иногда смущают новичков, но здесь нет никакого подвоха: разомкнутая цепь не имеет электрического соединения между своими концами, а короткозамкнутая содержит просто кусок провода. Источники напряжения обозначаются символами, показанными на рис. 1.9 .
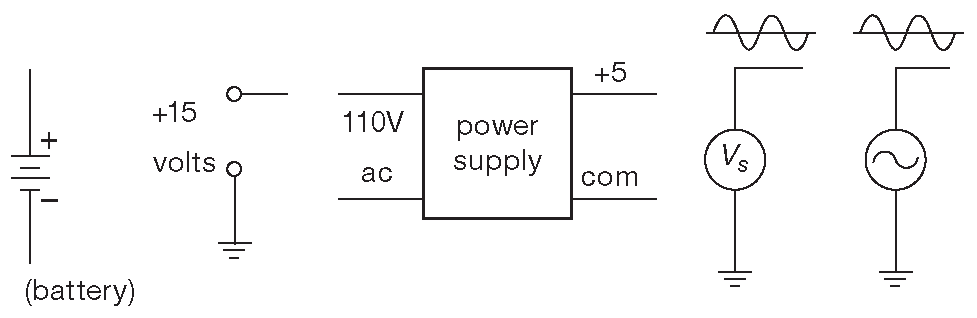
Рис. 1.9 Источники напряжения могут выдавать как постоянное (dc), так и переменное (ac) напряжение
Идеальный источник тока - двухвыводной чёрный ящик, поддерживающий постоянный ток через внешнюю схему, подключённую к своим выходным терминалам, независимо от сопротивления нагрузки. Чтобы выполнить данную задачу устройство должно обеспечить на выводах любое необходимое напряжение. Настоящие источники тока ( редко упоминаемые в других учебниках ) имеют ограничение по максимальному напряжению на выводах ( диапазон возможных напряжений называется рабочим диапазоном ) и, кроме того, не могут обеспечить высокую стабильность тока. Источники тока «любят» короткозамкнутые цепи и «ненавидят» разомкнутые. Для обозначения источников тока на схемах используют символы, показанные на рис. 1.10 .
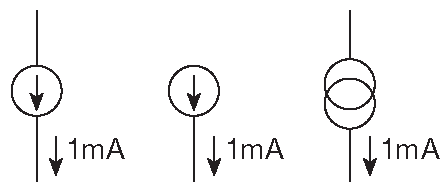
Рис. 1.10 Символы источников тока
==9
Батарея является зримым эквивалентом источника напряжения, а для источника тока такого примера из жизни нет. Стандартный элемент «D» даёт 1.5 V и имеет эквивалентное последовательное сопротивление 0.25 Ω . Его запас энергии примерно равен 10'000 ватт-секунд. Характеристики постепенно ухудшаются по мере использования, и в конце жизни напряжение может упасть до 1.0 V , а последовательное сопротивление вырасти до нескольких ом. Совсем несложно сделать источник напряжения с гораздо лучшими характеристиками [* если, конечно, не учитывать шумовые параметры см. рис. 8.123 ] , о чём ещё будет рассказано в теме обратной связи и в Части _9 . Если исключить важный класс носимых приборов, батареи в электронных устройствах используются нечасто.
1.2.5 Эквивалентная схема Тевенина
Теорема Тевенина утверждает, что любая схема, состоящая из резисторов и источников напряжения и имеющая только два вывода, может быть сведена к эквивалентной схеме из одного резистора \(R_{Th}\) , включённого последовательно с источником напряжения \( V_{Th}\) 12 . Это весьма примечательное обстоятельство. Любое количество батарей и резисторов можно сымитировать с помощью всего одной батареи и одного резистора ( рис. 1.11 ). Есть смежная теорема Нортона , которая гласит, что эквивалентная схема может состоять из источника тока и параллельного ему резистора.
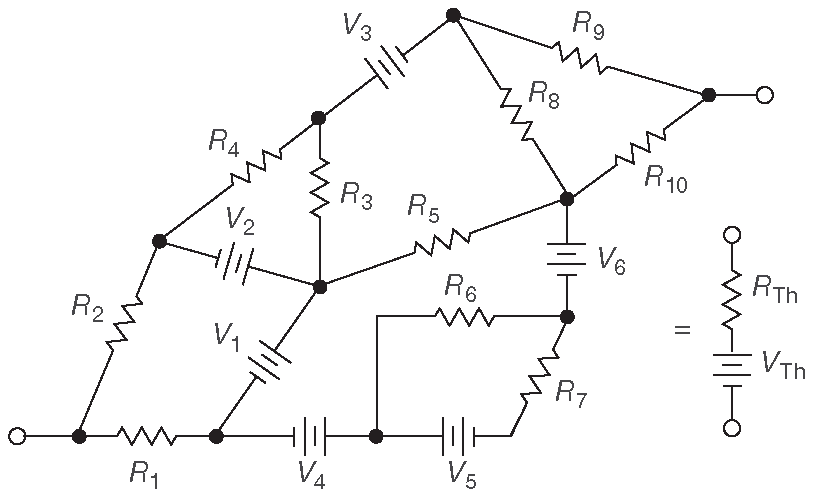
Рис. 1.11 Эквивалентная схема Тевенина
Как найти эквивалентные элементы цепи Тевенина \(R_{Th}\) и \( V_{Th}?\) Это не сложно. \( V_{Th}\) - напряжение на выводах эквивалентной схемы в разомкнутом состоянии. Для идентичных цепей, то оно должно быть равно напряжению на выводах исходной схемы в разомкнутом состоянии. Данную величину можно найти аналитически, если схема известна, или измерить непосредственно. \(R_{Th}\) находится через ток короткого замыкания, который равен \( V_{Th}/R_{Th}:\) \[ V_{Th} = V(open ), \qquad R_{Th}=\frac{V(open )}{I( short )} \qquad \qquad [1.7] \]
Попробуем применить данный метод к делителю напряжения, у которого тоже должен быть эквивалент Тевенина.
[* Объяснение эквивалентного сопротивления делителя]
1. Напряжение на разомкнутых выводах: \[ V=V_{in}\frac{R_2}{R_1+R_2} \] 2. Ток короткого замыкания: \[ I_{sc}=\frac{V_{in}}{R_1} \]
Отсюда, эквивалентная схема Тевенина состоит из источника напряжения \[ V_{Th}=V_{in}\frac{R_2}{R_1+R_2} \qquad \qquad [1.8] \] и последовательного резистора \[ R_{Th}=\frac{R_1R_2}{R_1+R_2} \qquad \qquad \quad [1.9] \]
( Результат в виде параллельного соединения резисторов \(R_1\) и \(R_2\) - не случайность. Причина станет ясна позднее. )
Из этого примера хорошо видно, что делитель напряжения не слишком хороший источник напряжения в том смысле, что его выходное напряжение сильно падает при подключении нагрузки. Как пример, разберите упражнение 1.10 . На данный момент известно всё, что надо знать для расчёта величины падения при заданном сопротивлении нагрузки. Надо подключить нагрузку и, используя теорему Тевенина, посчитать новое выходное напряжение, имея в виду, что новая схема ни что иное, как делитель напряжения ( рис. 1.12 ).
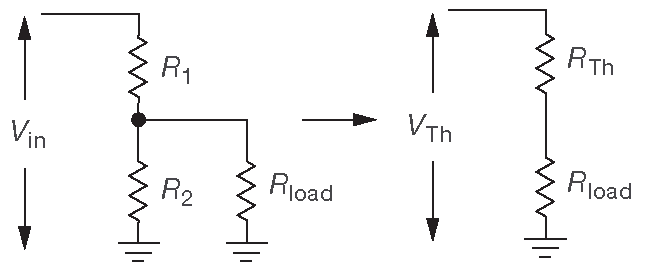
Рис. 1.12 Преобразование Тевенина для делителя напряжения
==10
Упражнение 1.10
Для схемы 1.12 \( V_{in}\) равно 30 V , а \(R_1\) и \(R_2\) по 10 kΩ . Требуется найти:
(a) выходное напряжение в отсутствие нагрузки ( напряжение с разомкнутой цепью );
(b) выходное напряжение с нагрузкой 10 kΩ ( схему при этом следует рассматривать как делитель, в котором нижний резистор образован параллельным соединением \(R_2\) и \(R_{load}\) ;
(c) эквивалентную схему Тевенина;
(d) повторить пункт (b), но с использованием теоремы Тевенина ( ответ должен совпадать с (b));
(e) мощность, рассеиваемую каждым резистором.
Мультиметры
Есть много приборов, позволяющих измерять напряжения и токи в схеме. Наиболее универсальный - осциллограф. Он позволяет видеть изменение напряжения во времени одновременно в нескольких точках схемы. Логические пробники и анализаторы предназначены для исследования цифровых устройств. Простые мультиметры позволяют измерять напряжение, ток и сопротивление, часто с хорошей точностью. Но это медленные приборы и не могут заменить осциллограф, когда интересно изменение напряжения. Мультиметры бывают двух видов: аналоговые, которые показывают результат движущимся по шкале указателем или цифровые, выдающие на дисплей данные в числовой форме.
Прежние ( практически полностью исчезнувшие ) авометры ( ампер-вольт-омметр - VOM ) использовали стрелочную измерительную головку ( с типичным током полной шакалы 50 μA ). Её внешний вид и начинку можно посмотреть в старых книгах, а сейчас достаточно знать, что они использовали поворот катушки с током в магнитном поле. Для измерения напряжения последовательно с головкой ставили резистор. Скажем, для отображения шкалы «0...1V» последовательно с головкой на 50 μA надо было поставить резистор 20 kΩ . Для бОльших напряжений требовались бОльшие резисторы. Такие приборы специфицировались значением 20'000 Ω/V , что означало, что они выглядят как резистор 20 kΩ , умноженный на напряжение полной шкалы на выбранном пределе. Ток полной шкалы таких вольтметров составлял \(\frac{1}{20000}\)A или 50 μA . Иначе говоря, вольтметр оказывал меньшее воздействие на схему на бОльших пределах, когда в измерительной цепи стоял резистор большего номинала. Схему измерения можно представить как делитель, где эквивалентный резистор Тевенина, замещающий измеряемую цепь, стоит в верхнем плече, а вольтметр [* измерительная головка и последовательный резистор] - в нижнем. В идеальном случае сопротивление последнего должно быть бесконечным.
Большинство современных мультиметров используют электронное усиление и при измерении напряжения имеют входное сопротивление от 10 до 1000 MΩ . Результаты выводятся на цифровой индикатор, а сам прибор называется цифровым мультиметром ( DMM ). Небольшое предупреждение: иногда входное сопротивление таких приборов очень велико на самом чувствительном пределе, но уменьшается на остальных. Скажем, типичное значение 1 GΩ на пределах «0.2 V» и «2V» и 10 MΩ на всех более высоких. Читайте паспортные данные! Но в любом случае параметры столь высоки, что для большинства схем эффект делителя будет пренебрежимо мал, причём его можно легко оценить. Типичный мультиметр имеет нижний предел в районе 1V и верхний - 1 kV для полной шкалы.
Обычные мультиметры способны измерять ток , и тоже на нескольких пределах. Идеальный измеритель тока должен иметь нулевое сопротивление 13 , чтобы не оказывать воздействие на измеряемую схему, т.к. включаются измерители тока последовательно. На практике пара десятых долей вольта на VOM или DMM картину не портит ( их зовут «нагрузка по напряжению» ). Для любого инструмента переключение предела выбирает низкоомный резистор, который перемыкает входные клеммы. Падение напряжения на нём составляет от 0.1 до 0.25 V для максимального тока на выбранном пределе. Это падение переводится в цифры на индикаторе 14 . Обычный набор диапазонов от 50 μA до 1A полной шкалы.
Кроме того, в состав мультиметра входит батарея, позволяющая измерять сопротивление. На резистор подаётся калиброванный ток, получившееся падение напряжения переводится в цифры. Измеряемые номиналы от 1 Ω и менее до 10 MΩ и более.
Важное предупреждение ! Не пытайтесь измерить «ток источника напряжения», засовывая щупы в розетку на стене. То же предупреждение касается и «внутреннего сопротивления» розетки. Сожжёте прибор и только.
Упражнение 1.7
Что покажет VOM 20'000 Ω/V на пределе «1V», если его подключить к источнику 1V с внутренним сопротивлением 10 kΩ ?
Что он покажет для средней точки делителя 10 kΩ+10 kΩ , подключённого к «жёсткому» ( т.е. с нулевым внутренним сопротивлением ) источнику 1V ?
Упражнение 1.8
Измерительная головка на 50 μA имеет внутреннее сопротивление 5 kΩ .
Какое шунтирующее сопротивление требуется для измерения тока 0...1A ?
Какое последовательное сопротивление требуется для измерения напряжения 0...10 V ?
Упражнение 1.9
Очень высокое внутреннее сопротивление цифровых мультиметров можно использовать для измерения очень низких токов ( даже если DMM не имеет такой опции непосредственно ). Предположим, что надо измерить небольшой ток «утечки» через сопротивление 1000 MΩ ( такой термин употребляется для описания очень малых токов, наличие которых крайне нежелательно, например, ток через изоляцию подземного кабеля ). Есть стандартный DMM с диапазоном «2V» постоянного напряжения и внутренним сопротивлением 10 MΩ , плюс источник на +10 V .
Как можно использовать этот набор для точного измерения сопротивления утечки?
1.2.5.A Эквивалентное сопротивление источника и нагрузка на схему
==11
Как только что было показано, делитель напряжения, питаемый постоянным напряжением, эквивалентен последовательному соединению меньшего по величине источника напряжения и какого-то резистора. Например, делитель 10 kΩ+10 kΩ , на который подано 30 V , будет в точности равен источнику 15 V с последовательным сопротивлением 5 kΩ ( рис. 1.13 ). Подключение нагрузочного резистора вызовет падение напряжения на выходе делителя - следствие ненулевого сопротивления источника ( это эквивалентное сопротивление Тевенина для делителя, которое подключено последовательно с источником напряжения ). Такое поведение чаще всего нежелательно. Решением будет создание «жёсткого» источника напряжения ( «жёсткий» в значении «не поддающийся под нагрузкой» ). Решить задачу можно, поставив в делитель низкоомные резисторы. Иногда этот грубый метод срабатывает, но правильнее было бы создать источник напряжения или, как его обычно называют, «источник питания» с использованием активных компонентов ( транзисторов или операционных усилителей ), что и будет сделано в Частях _2 , _3 , _4 . Такой подход позволяет создавать источники напряжения с внутренним сопротивлением ( эквивалентом Тевенина ) на уровне тысячных долей ома, без избыточного тока и тепла, рассеиваемого низкоомным делителем с такими же параметрами. Кроме того, имея активный источник питания легко сделать выходное напряжение подстраиваемым. Теме источников питания посвящена Часть _9 .
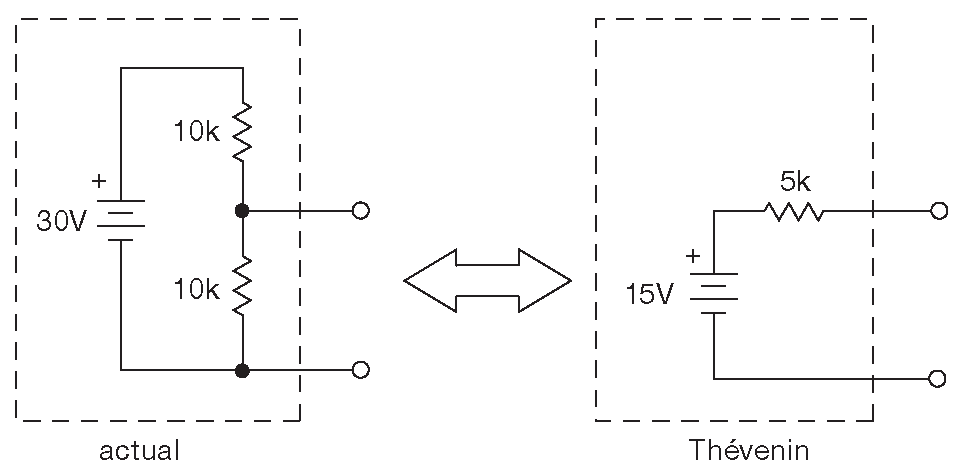
Рис. 1.13 Пример преобразования делителя напряжения
Принцип эквивалентного внутреннего сопротивления применим ко всем видам источников, а не только к батареям и делителям. Все источники сигналов - генераторы, усилители, датчики и т.д. имеют внутреннее эквивалентное ( выходное ) сопротивление. Подключение к ним нагрузки меньшей или даже сравнимой с внутренним эквивалентным сопротивлением, самым плачевным образом скажется на уровне сигнала. Нежелательное понижение напряжения ( или сигнала ) называется «просадкой источника». Таким образом, надо стремиться выдерживать соотношение R(load )≫R(out ) , чтобы понизить эффект делителя для сигнала ( рис. 1.14 ) 15 . Дальше будет представлено несколько примеров. Примером идеальной нагрузки является измерительные инструменты, вроде вольтметра или осциллографа.
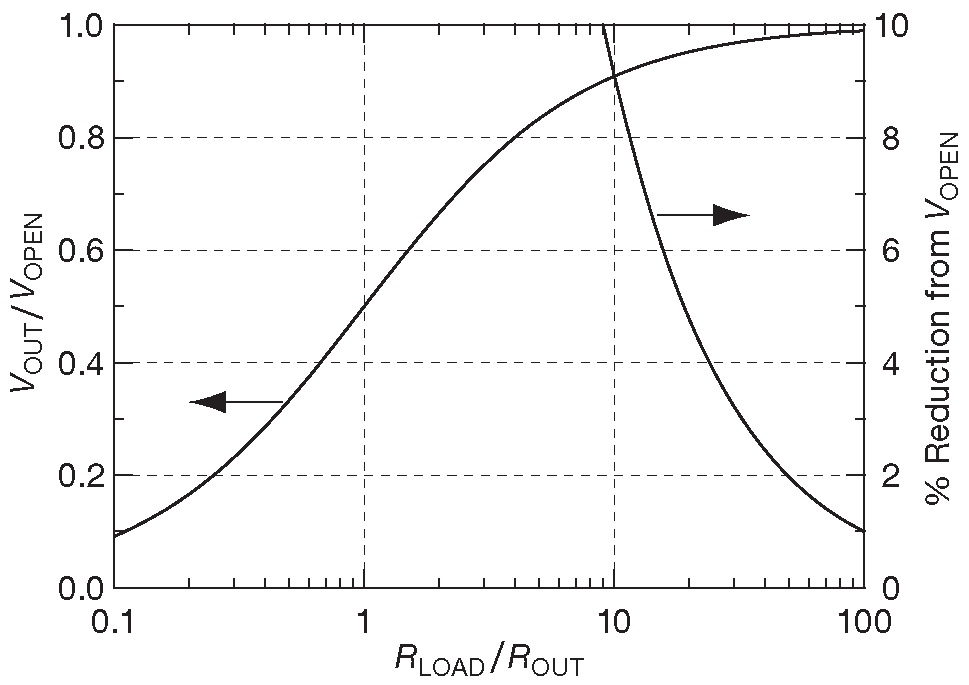
Рис. 1.14 Чтобы минимизировать ослабление сигнала источника по сравнению с ненагруженным выходом, надо удерживать сопротивление нагрузки большим по отношению к выходному сопротивлению источника
Небольшое отступление о словесном оформлении. Часто можно слышать выражения «сопротивление, смотрящее на делитель» или «выход видит такую-то нагрузку», как будто у схемы есть глаза. Это нормально и достаточно удобно для сообщения, о каком конкретно сопротивлении идёт речь, если указать, кто именно «смотрит» 16 .
[* Очень мило, если не считать того, что по-английски “the resistance looking into the voltage divider” – «сопротивление, заглядывающее в делитель напряжения» должно переводиться как «сопротивление со стороны делителя» ( «внутреннее сопротивление делителя, которое куда-то смотрит» ). Хорошо, что я понимаю, о чём речь, а так ни за что бы не догадался, как правильно переводится] .
1.2.5.B Передача мощности
Есть интересный вопрос: какое сопротивление должна иметь нагрузка, чтобы при заданном сопротивлении источника ей была бы передана максимальная мощность? ( Термины «сопротивление источника», «внутреннее сопротивление» и «эквивалентное сопротивление Тевенина» - синонимы ). Если \(R_{load}\space\)=0 или \(R_{load}=∞\) , мощность в нагрузку не поступает. Для \(R_{load}\space\)=0 и \( V_{load}\space\)=0 , поэтому \( P_{load}\space\)=0×\(I_{load}\space\)=0 . Для \(R_{load}=∞\) имеем \( V_{load}=V_{source}\) , значит, \(I_{load}\space\)=0 и \( P_{load}=V_{source}\space\)×0=0 . Максимум где-то между этими точками.
Упражнение 1.11
Покажите, что \(R_{load}=R_{source}\) обеспечивает максимальную передаваемую мощность. Если не можете в математику, то просто примите данное утверждение на веру.
==12
Чтобы не создать неправильного впечатления повторим опять: обычно схемы проектируются так, чтобы сопротивление нагрузки было гораздо больше сопротивления источника сигнала [* с учётом сноски #15 можно добавить, что речь идёт об источнике напряжения, а сигнал выражается в вольтах. Для токовых сигналов картина обратная] .
1.2.6 Сопротивление для малого сигнала
В электронике часто приходится иметь дело со схемами, в которых ток не пропорционален напряжению. В такой ситуации говорить о сопротивлении бессмысленно, т.к. отношение \( V/I\) не является константой [* закон Ома не выполняется] . Для таких компонентов полезно бывает знать график зависимости «V-I» ( вольтамперную характеристику ) или отношение изменения приложенного напряжения к изменению результирующего тока \(ΔV/ΔI\) ( или \( dV/dI\) ) . Эта величина выражается в единицах сопротивления - омах и подменяет классическое сопротивление в расчётах. Величина называется «динамическим сопротивлением» .
1.2.6.A Стабилитроны
В качестве примера рассмотрим диод Зенера или стабилитрон , вольтамперная характеристика которого приведена на рис. 1.15 . Стабилитроны используются для получения постоянного напряжения где-либо в схеме. Сделать это можно, подав на прибор примерно постоянный ток 17 . По графику 1.15 видно, что изменение приложенного тока вызывает соответствующее, но меньшее по амплитуде, изменение напряжения [* пунктирные линии в области отрицательного тока и отрицательного напряжения ( 1.15B III квадрант )] . Важно знать, как изменится напряжение на стабилитроне при изменении тока. Это позволяет получить «коэффициент стабилизации» при передаче изменений со входа на выход. В спецификации на стабилитрон есть параметр «динамическое сопротивление» , которое задаётся при определённом токе. Например, динамическое сопротивление может составлять 10 Ω при 10 mA на номинальном напряжении стабилитрона 5V . Зная определение динамического сопротивления, можно выяснить, что изменение рабочего тока на 10% вызовет изменение напряжения \[ ΔV=0.1×( R_{dyn} · ΔI )=0.1×(10·0.01 )=10 mV \] или \[ \frac{ΔV}{V}=\frac{10 mV}{5V}=0.002=0.2\%. \]
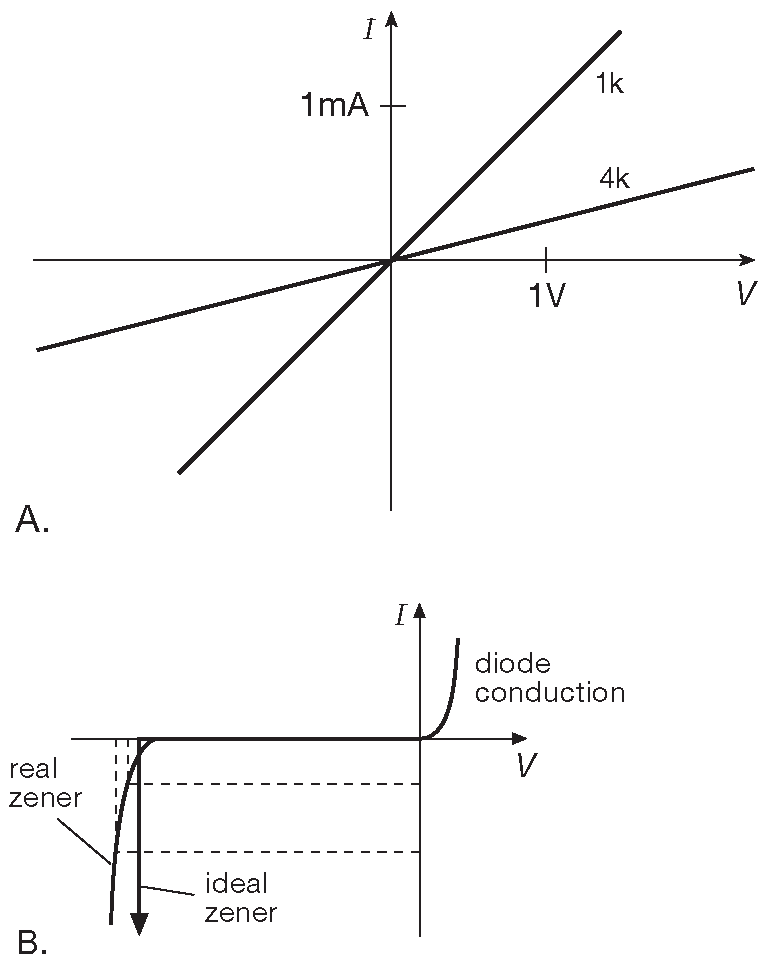
Рис. 1.15 Вольтамперные характеристики. (A) Резистор ( линейный компонент ). (B) Стабилитрон ( нелинейный компонент )
Это хорошая стабилизация. В такого рода схемах ток задаётся резистором, подключенным к какому-либо более высокому напряжению, см. рис. 1.16 .
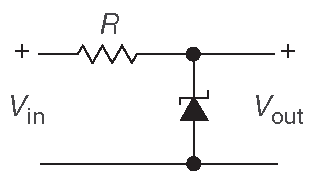
Рис. 1.16 Регулятор на стабилитроне
Тогда \[ I=\frac{V_{in}-V_{out}}{R}, \qquad Δ I = \frac{Δ V_{in}-Δ V_{out}}{R}, \] значит, \[ Δ V_{out}=R_{dyn} Δ I= \frac{R_{dyn}}{R}( Δ V_{in}- Δ V_{out} ) \] или \[ Δ V_{out}=\frac{R_{dyn}}{R+R_{dyn}} Δ V_{in}. \]
==13
Мы вновь получили формулу для делителя напряжения. Теперь для изменений напряжения. Схема ведёт себя подобно делителю, в котором стабилитрон заменяется его динамическим сопротивлением при заданном токе. Это именно то, для чего динамическое сопротивление и предназначено. Например, для схемы 1.16 имеем входное напряжение, изменяющееся от 15 до 20 V . Используем стабилитрон 1N4733 ( 5.1V , 1W ), чтобы сделать источник питания на 5.1V . Выбираем \(R\)=300 Ω по максимальному паспортному значению тока 50 mA : (20 V–5.1V)/50 mA=300 Ω . Теперь можно оценить коэффициент стабилизации вход-выход [* пропорции, в которой изменение на входе передаётся на выход] , используя максимальное паспортное значение динамического сопротивления 7.0 Ω при 50 mA: . При заданном изменении рабочего напряжения ток будет меняться от 50 до 33 mA . Изменение на 17 mA приведёт к изменению на выходе \(ΔV=R_{dyn} Δ I\)=0.12 V .
Динамическое сопротивление стабилитронов меняется вместе с током и имеет примерно обратно пропорциональную зависимость. Имеются микросхемы, созданные на замену стабилитронам. Такие «двухвыводные источники опорного напряжения» имеют отличные параметры: гораздо меньшее динамическое сопротивление ( менее 1 Ω даже для токов порядка 0.1 mA , что на три порядка лучше, чем у обычных стабилитронов ) и высокую термостабильность ( лучше, чем 0.01%/°C ). Дополнительные данные по стабилитронам и опорным источникам можно найти в §2.2.4 и §9.10 .
Более высокие значения коэффициента регуляции можно получить, если питать стабилитрон от источника тока, который в идеальном случае имеет \(R_{incr}= ∞\) ( т.е. выдают один ток, независимо от напряжения ). Но источник тока - достаточно сложное устройство, и поэтому часто заменяется обычным резистором. При использовании стабилитронов стоит помнить, что низковольтовые модели ( например, на 3.3 V ) имеют плохие параметры в терминах зависимости напряжения от тока [* т.е. динамического сопротивления - оно высокое ] , см. рис. 1.17 . Если требуется низкое напряжение надо использовать двухвыводные опорные источники ( §9.10 ) [* или использовать прямое ( когда светится ) падение на подходящем светодиоде: у них тоже всё хорошо с динамическим сопротивлением см. рис. 2.8 ] .
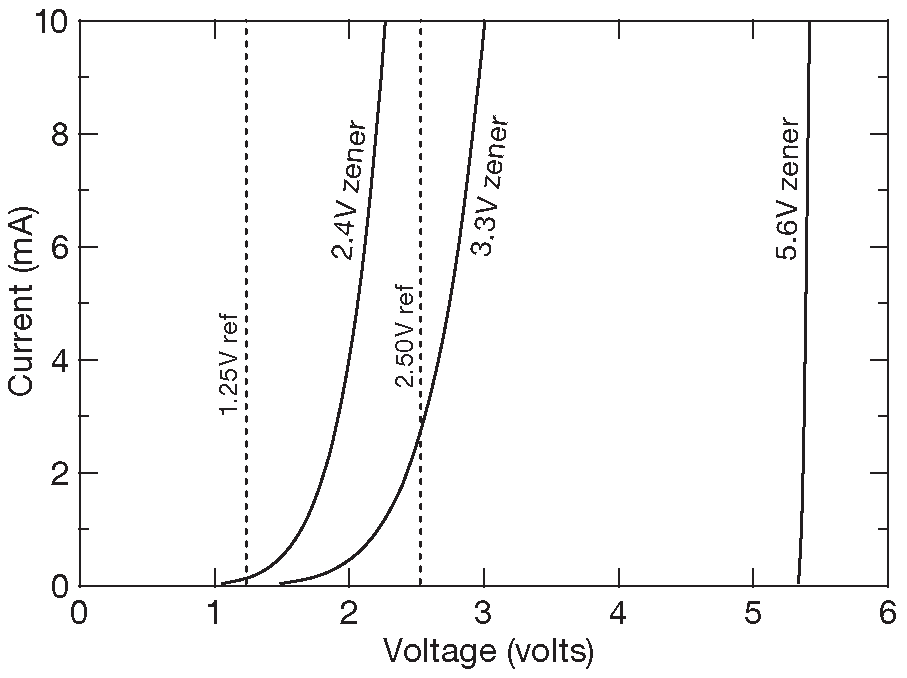
Рис. 1.17 По данным вольтамперным характеристикам видно, что низковольтовые стабилитроны высокими параметрами не блещут ( данные для трёх моделей из ряда 1N5221-1N5267 ), особенно если сравнить их с данными интегральных «опорных источников» ( LM385Z-1.2 и LM385Z-2.5, см. §9.10 и табл. 9.7 ). Но в районе 6V ( 5.6 V у 1N5232B и 6.2 V у 1N5234B ) стабилитроны имеют очень крутой загиб АЧХ и являются вполне рабочими компонентами
1.2.7 «Горячий» пример
Некоторые люди любят подкрутить термостат на более высокую температуру, а другие наоборот - хотят похолоднее. Вот маленькая схема ( рис. 1.18 ), которая даст им всем знать, когда пора скандалить. Она зажигает красный светодиод ( LED ), если температура в комнате поднялась выше 30°C . Заодно схема поясняет, как использовать простой делитель напряжения ( вместе с ещё более простым законом Ома ) и работать со светодиодом, который похож на стабилитрон и иногда используется вместо последнего.
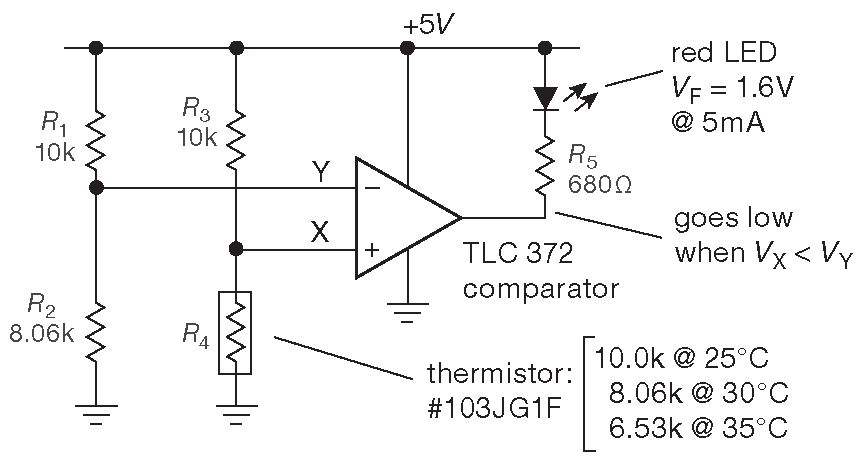
Рис. 1.18 Светодиод зажигается, когда температура превышает 30°C . Компаратор ( разбирается в Части _4 и 12 ) выдаёт на выходе уровень земли, если напряжение в точке «X» меньше, чем в точке «Y». \(R_4\) - термистор - резистор с очень большим отрицательным температурным коэффициентом, е.е. его сопротивление уменьшается с ростом температуры со скоростью 4%/°C
Треугольник по центру - схемный символ компаратора . Это удобное устройство ( §12.3 ), которое переключает выход в зависимости от знака разницы напряжений на двух своих входах. Датчиком температуры служит \(R_4\) , который уменьшает сопротивление с коэффициентом 4%/°C и имеет номинальное значение 10 kΩ при 25°C . Он стоит в нижнем плече делителя \(R_3R_4\) , средняя точка которого сравнивается с не зависящим от температуры значением с пары \(R_1R_2\) . Когда температура достигнет 30°C , точка «X» будет иметь меньший потенциал, чем точка «Y», поэтому компаратор выдаст на выходе уровень земли.
А на выходе висит светодиод, который с электрической точки зрения напоминает стабилитрон на 1.6 V . Когда через него течёт ток, светодиод светится, при этом напряжение на его нижнем [* по схеме ] выводе составляет +5V–1.6 V=+3.4 V . Поэтому, чтобы задать ток 5 mA через светодиод, надо поставить последовательный резистор \(R_5\) с номиналом 3.4 V/5 mA=680 Ω .
Можно сделать граничную температуру настраиваемой, заменив \(R_2\) на последовательное соединение переменного и постоянного резистора на 5 kΩ каждый [* постоянный со стороны земли ] . Позднее будет показано, что полезен будет и некоторый гистерезис . Он позволит компаратору увереннее выбирать состояние. Отметим, что схема нечувствительна к изменению питающего напряжения, т.к. сравнивает разницу двух его фрагментов. Это логометрическая техника, которая ещё не раз встретится в книге.
==13
12 [* Да, это тоже ссылка номер «двенадцать» ] . Для интересующихся в Приложении _D есть доказательство. <-
13 Это прямо противоположно представлениям об идеальном измерителе напряжения, который должен выглядеть со стороны измерительных концов как бесконечное сопротивление. <-
14 Отдельный класс измерителей тока, называемых электрометрами работают с очень низкими уровнями напряжений ( до 0.1V ), используя обратную связь, о которой будет разговор в Части _2 и _4 . <-
15
Есть два важных исключения из этого универсального правила.
(1) Источник тока имеет высокое ( в идеале бесконечное ) внутреннее сопротивление и должен работать на низкоомную нагрузку.
(2) При работе на радиочастотах и с линиями передачи, где требуется «согласовывать импедансы», т.е. добиваться соотношения \(R_{load}=R_{out}\) , чтобы не допустить появления отражений и потери мощности. Линии передачи объясняются в Приложении _H .
<-
16 Хотя «очеловечивание» глубоко проникло в инженерную и учёную среду, не забывайте о предупреждении: «не очеловечивайте компьютер, ему это не нравится». <-
17 Стабилитроны относятся к классу диодов [* стабилитрон = диод Зенера ] или выпрямителей . Это важный класс компонентов, которые будут рассматриваться в §1.6 ( и вообще везде ). Идеальный диод или выпрямитель работает как идеальный проводник для тока, текущего в одном направлении, и идеальный изолятор для обратного тока. Это дорога с односторонним движением для токов. <-

