Приложение D. Теорема Тевенина
==1107
В Части _1 ( §1.2.5 ) формулировалась, но не доказывалась, теорема Тевенина. Она гласит, что любая цепь, имеющая два внешних вывода и состоящая исключительно из резисторов, батарей и источников тока, которые могут соединяться между собой любым способом, эквивалентна и неотличима от двухвыводной цепи, состоящей из одной батареи \( V_{Th}\) и одного последовательно включённого резистора \(R_{Th}\) _1 , см. рис. D.1 . Тогда она была принята без доказательств, т.к. это противоречило целям и духу книги: авторы ничего не доказывают , вместо этого показывают, как проектировать схемы. Но здесь будет сделано исключение, потому что надо же доказать хоть что-нибудь ?!
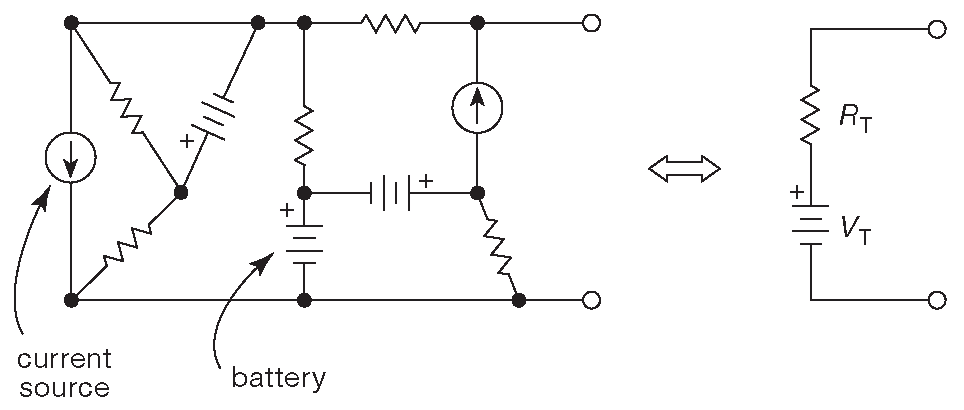
Рис. D.1 Теорема Тевенина: резистор последовательно с батареей может заменить двухвыводную цепь любой сложности, собранной из резисторов, батарей и источников тока
D.1 Доказательство
Для линейных элементов схемы ( здесь резисторов ) «узловые уравнения» ( соотношения Кирхгоффа для напряжений и токов ) являются множеством линейных уравнений. Т.е. можно найти любую величину - напряжение или ток, которая зависит от всех «независимых источников» ( батарей и источников тока ), подключая такие источники к схеме один за другим и складывая эффекты от их воздействия. ( Алгоритм полностью аналогичен поиску суперпозиции нескольких величин, например, электрического поля, образованного множеством зарядов ). Этот приём часто используется при анализе схем.
Здесь мы хотим подменить напряжения и токи исходной схемы более простым эквивалентом Тевенина - одной батареей и одним последовательным резистором. Предположим, что установлено, как именно зависит \( V \) от \(I\) , путём подключения внешнего тока \(I_{ext}\) , который течёт через два вывода схемы и измеряя напряжение на этих выводах. \( V \) зависит от \(I_{ext}\space \) плюс от всех внутренних батарей ( \( V_{in}\) ) вместе с внутренними источниками тока ( \(I_{in}\) ) .
- Приравняем нулю все внутренние источники: \( V_{int}\) =0 и \(I_{int}\) =0 . Для этого заменим все внутренние батареи короткозамкнутой цепью, а все источники тока - разрывами цепи. Теперь подадим \(I_{ext}\space\) и зафиксируем \( V_1\) .
- Зададим \(R_T=V_1/I_{ext}\space\) ( они должны быть пропорциональны т.к. схема линейная )
- Теперь выключим внешний ток ( \(I_{ext}\) =0 ) и включим внутренние батареи и источники тока. Зафиксируем \( V_2\) , которое назовём \( V_T \) .
- Наконец, благодаря принципу суперпозиции, должно выполняться соотношение \[ V_{actual} = V_1 + V_2 = I_{ext}R_T + V_T. \]
Соотношение выполняется для любого \(I_{ext}\space\) , и это именно то, что даёт эквивалентная схема Тевенина, которая подключена к любой ( не обязательно линейной ) нагрузке, см. рис. D.2 .
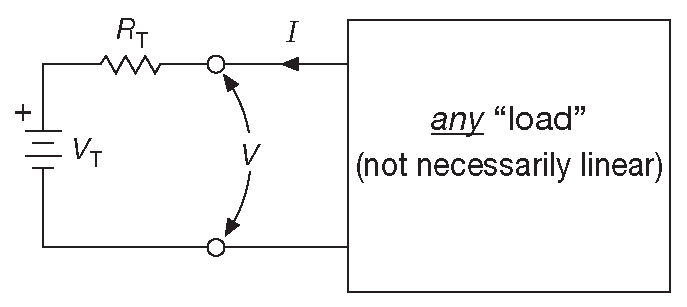
Рис. D.2 Эквивалентная цепь Тевенина работает в точности так же, как исходная цепь, независимо от вида нагрузки
Подводя итог.
- Сначала находится \( V_{OC} \) для ненагруженной схемы. Это будет \( V_T \) .
- Затем находится ток короткого замыкания \(I_{SC}\) , который равен отношению \( V_T/R_T\) . Другими словами, \( V_T=V_{OC}\) , \(R_T=V_{OC}/I_{SC}\) .
Если схема известна, можно получить результат аналитически, если есть только чёрный ящик, то результат получается прямым измерением.
D.1.1 Два примера - делители напряжения
На рис. D.3 и D.4 показаны два простых примера - варианты резистивного делителя. Что интересно, их эквивалентные схемы различны, притом даже, что номиналы резисторов и напряжения \( V_{OC} \) одинаковые.
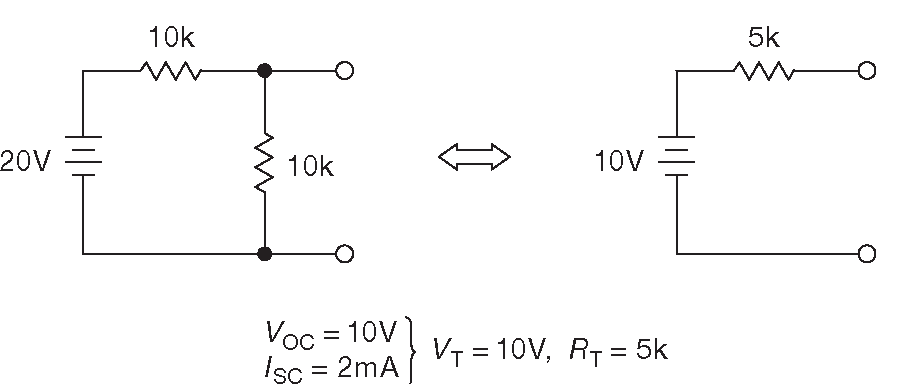
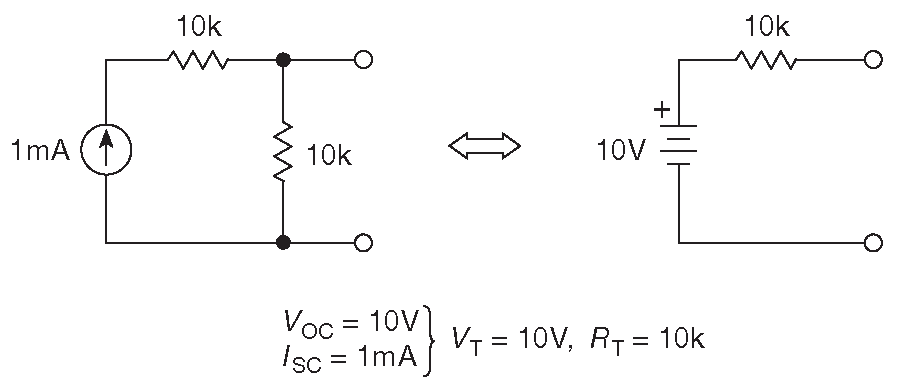
Рис. D.3 Эквивалентная схема простого резистивного делителя. Отметим, что \(R_T\) равен параллельному сопротивлению резисторов ( как если бы источник напряжения был заменён коротким замыканием )
Рис. D.4 Здесь эквивалентная схема не идентична параллельному сопротивлению резисторов делителя. Эквивалентное сопротивление равно одному резистору, параллельному нагрузке ( как если бы источник тока заменили бы разрывом цепи )
==1108
D.2 Теорема Нортона
Схему Тевенина можно заместить схемой Нортона, которая состоит из источника тока \(I_N\) и параллельного ему резистора \(R_N\) ( рис. D.5 ). Можно доказать, что \(I_N=I_{SC}\) , а \(R_N=R_T=V_{OC}/I_{SC}\) . Таким образом, для двух примеров выше эквивалентные схемы будут выглядеть как на рис. D.6 .
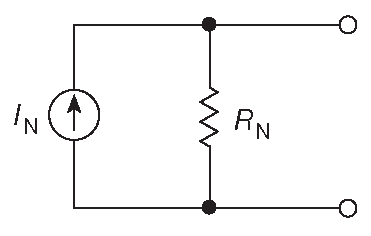
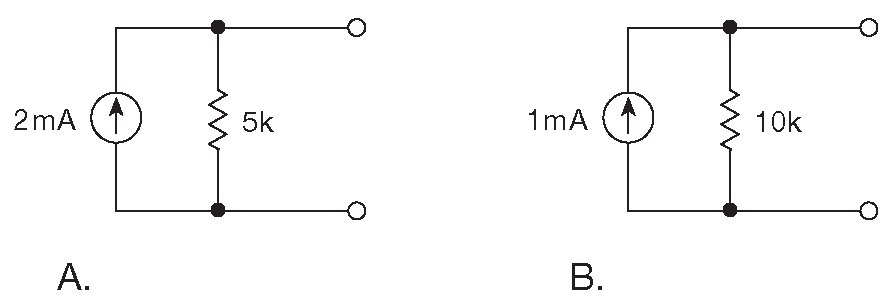
Рис. D.5 Эквивалентная схема Нортона: источник тока с параллельным резистором
Рис. D.6 Эквивалентные схемы Нортона для примеров D.3 (A) и D.4 (B)
D.3 Другой пример
На рис. D.7 показана более сложная схема. Для неё \( V_{OC} \) =25 V, т.к. нижний конец резистора 10 kΩ опирается на +10 V , а сверху в него втекает 1.5 mA . Ток \(I_{SC}\) =2.5 mA , т.к. имеем 10 V падения на 10 kΩ плюс два источника тока. Отсюда можно вывести показанную эквивалентную схему.
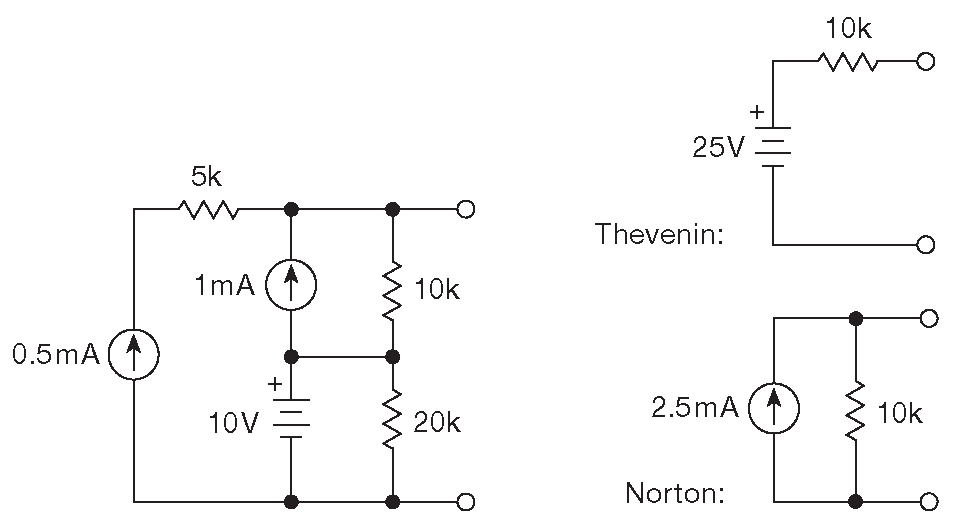
Рис. D.7 Схемы Тевенина и Нортона для более сложного примера
D.4 Теорема Миллмана
Есть ещё одна близкая и полезная теорема - теорема Миллмана, известная также как теорема о параллельных генераторах. Её удобно использовать при разборе схем с несколькими параллельными ветвями. Рассмотрим рис. D.8 . Набор входных напряжений \( V_i\) объединяется через резисторы \(R_i\) , создавая выходное напряжение \( V_o\) . Последнее равно \( V_o=(Σ V_iG_i )/Σ G_i\) , где \( G_i\) - проводимости ветвей \( G_i≡ 1/R_i\) . Входные напряжения, естественно, могут включать потенциал земли, образуя делитель напряжения. Теорема Миллмана, входящая в класс более универсальных теорем теории цепей, может быть обобщена для включения в рассмотрение токов \(I_k\) , сумма которых прибавляется к числителю ( а вот последовательное сопротивление, если таковое обнаружится, в знаменателе не появится ).
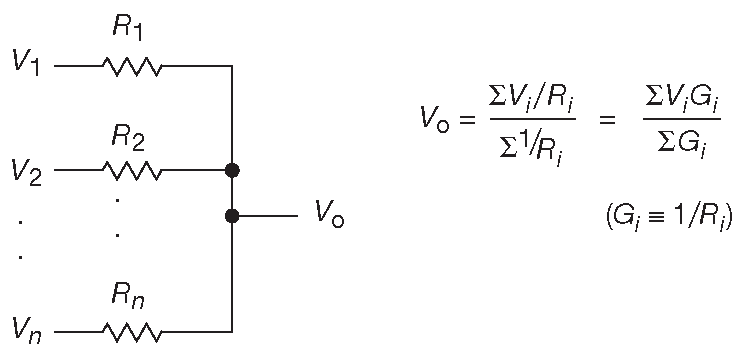
Рис. D.8 Теорема Миллмана для параллельных цепей
==1108
1 Аналогичная теорема Нортона сводит такую цепь к параллельному соединению источника тока \(I_N\) и резистора \(R_N\) . <-

