1.2 (I) Напряжение, ток и сопротивление
==1
1.2.1 Напряжение и ток
Есть две физические величины, которые требуют учёта в любой электронной схеме: ток и напряжение. Обычно они меняются во времени, в противном случае не происходило бы ничего интересного.
==2
- Напряжение
- ( символ \( V \) , иногда \( E\) ) . Официально напряжение между двумя точками - это энергия ( работа, которую надо совершить ), необходимая для перемещения единичного положительного заряда из точки с более отрицательным потенциалом к точке с более положительным. Аналогично, это энергия, высвобождающаяся, когда единичный положительный заряд перемещается от высокого потенциала к низкому _2 . Напряжение также называют разницей потенциалов или электродвижущей силой - ЭДС ( EMF ). Единицей измерения служит вольт . Работать обычно приходится с вольтами ( V ) , киловольтами ( kV=\(10\space^3V\) ) , милливольтами ( mV=\(10^{-3}V\) ) и микровольтами ( μV=\(10^{-6}V\) ) . 1 джоуль - работа, которая совершается при перемещении заряда в 1 кулон между точками с разницей потенциалов 1 вольт. Кулон - единица заряда, примерно эквивалентная заряду \( 6×10\space^{18}\) электронов. Встречаться с нановольтами ( nV=\(10^{-9}V\) ) и мегавольтами ( MV=\(10\space^6V\) ) приходится редко.
- Ток
- ( символ \(I\) ) . Ток - мера интенсивности, с которой заряды проходят через какую-либо точку. Измеряется в амперах . Работать приходится с амперами ( A ) , миллиамперами ( 1 mA=\(10^{-3}A\) ) , микроамперами ( 1 μA=\(10^{-6}A\) ) , наноамперами ( 1 nA=\(10^{-9}A\) ) и иногда с пикоамперами ( 1 pA=\(10^{-12}A\) ) . Ток 1A эквивалентен прохождению заряда 1 кулон за 1 секунду. Принято считать, что ток течёт из точки с более положительным потенциалом в точку с более отрицательным, хотя «реальные» электроны движутся в противоположном направлении.
Важное замечание . В соответствии с этими определениями ток течёт через что-то, а напряжение прикладывается между чем-то. Поэтому правильно говорить о напряжении между точками или токе через соединение или схему.
Фразы, подобные «напряжению через резистор», бессмысленны. Тем не менее, часто говорят о напряжении в какой-либо точке схемы. Такое утверждение надо понимать как напряжение между указанной точкой и «землёй» - неким соединением в схеме, с которым сравниваются все остальные потенциалы.
Напряжение создаётся в результате работы по заряду батареи ( устройства, в котором проходит электрохимическое преобразование энергии ), с помощью генераторов ( преобразование механической энергии в электромагнитную ), солнечных элементов ( преобразование фотонов в электроны ) и т.д. Ток появляется , когда к чему-либо прикладывают напряжение.
Здесь пора бы поинтересоваться, как «увидеть» напряжение или ток? Наиболее удобным и универсальным прибором является осциллограф, который позволяет наблюдать напряжения ( и иногда токи ) в схеме в виде функций времени _3 . В скором времени начнётся обсуждение сигналов, где будут плотно задействованы осциллограф и вольтметр, а в данный момент с осциллографом можно познакомиться в Приложении _O , а вольтметр появится на врезке позднее.
В электронных устройствах компоненты соединяются между собой проводами - металлическими проводниками, каждой точке которых имеется одно и то же напряжение относительно земли _4 . Данный вопрос упомянут прямо сейчас, чтобы стало понятно, что готовые устройства не обязаны походить на собственные электронные схемы, потому что благодаря проводам компоненты можно сдвигать друг относительно друга.
[* Нельзя не отметить существовавшую всегда, но активизировавшуюся в последнее время, тенденцию изображать схемные элементы в виде физических компонентов. Особенно «удобен» такой подход в случае микросхем. Читатель призывается к изживанию в себе «адруинных» элементов сознания и переходу на нормальную конструкторскую документацию, см. Приложение _B рис. B.4 или B.5 ] .
Несколько простых правил для токов и напряжений.
- Сумма токов, втекающих в точку равна сумме токов, вытекающих из неё ( закон сохранения заряда ) [* в точке не накапливается заряд] . Иногда это правило зовётся законом Кирхгоффа для токов [* или Первый закон Кирхгоффа ] . Инженеры предпочитают называть такие точки узлами . Следствием из данного правила является одинаковая величина тока, текущего через любой участок последовательной схемы ( цепочки двухвыводных устройств, включённых одно за другим ).
- Элементы, включённые параллельно ( рис. 1.1 ) имеют одинаковые напряжения на своих концах. Иначе говоря, сумма падений напряжений между точками «A» и «B» по одному пути эквивалентна сумме падений по другому пути и равна напряжению между точками «A» и «B». Официальная формулировка: сумма падений напряжений по замкнутому контуру равна нулю. Это закон Кирхгоффа для напряжений [* или Второй закон Кирхгоффа ] .
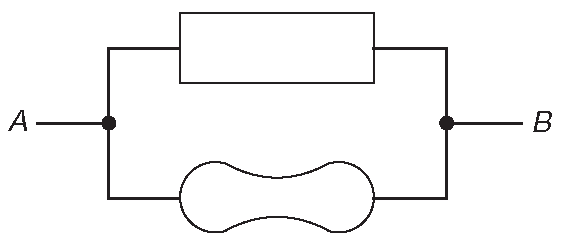
Рис. 1.1 Параллельное соединение
-
Мощность ( энергия за единицу времени ), потребляемая устройством равна \[ P = VI \qquad \qquad \qquad [1.1] \]
Для \( V \) в вольтах, а \(I\) в амперах \( P\) будет в ваттах. Поэтому, например, ток, текущий через 60-ваттную лампу накаливания, включённую в 120 V , равен 0.5 A . Ватт - это джоуль в секунду ( 1W=1J/s ) .
Мощность превращается в тепло или в механическую энергию ( моторы ), или в излучение ( лампы, передатчики ), или в запасённую энергию ( батареи, конденсаторы, катушки индуктивности ). Вопрос утилизации тепла, выделяющегося в сложных системах ( например, в больших вычислительных комплексах ), может быть очень существенным элементом разработки.
==3
Скоро придётся иметь дело с изменяющимися напряжениями и токами, и простое уравнение \( P=VI\) будет подправлено для учёта средней мощности, но мгновенная мощность считается именно так.
Кстати, никто не называет ток «амперажем», это очень колхозный диалект _5 . То же самое относится к «оммажу» _6 , если говорят о сопротивлении, о котором идёт речь в следующем параграфе.
1.2.2 Зависимость между напряжением и током: сопротивление и резисторы
Это долгая и интересная история. Речь идёт об основах электроники. В первом приближении требуется сделать устройство с нужной зависимостью тока от напряжения, используя имеющиеся компоненты. Как-то:
- резистор ( ток просто пропорционален напряжению ),
- конденсатор ( ток пропорционален изменению напряжения ),
- диод ( ток течёт в одном направлении ),
- термистор ( термочувствительный резистор ),
- фоторезистор ( светочувствительный резистор ),
- тензорезистор ( резистор чувствительный к изгибу ).
Есть ещё интересные трёхвыводные компоненты - транзисторы и им подобные, в которых ток, текущий через два терминала, управляется напряжением, поданным на третий. Все эти экзотические приборы будут постепенно вводиться в оборот. Начнём с наиболее прозаического ( и шире всего используемого ) элемента схем - резистора ( рис. 1.3 ).

Рис. 1.3 Схемное изображение резистора
1.2.2.A Сопротивление и резисторы
==4
Известен интересный факт: ток через металлический проводник ( или иной материал хоть сколь-нибудь проводящий ) пропорционален напряжению на его концах. В качестве проводников в схемах используются достаточно толстая проволока, чтобы падение напряжения на ней было совершенно незначительным. Это нисколько не единый закон проводимости для всех объектов. Например, ток через неоновую лампу очень нелинеен и равен нулю до какого-то критического значения, выше которого начинает очень резко расти. То же происходит с разными специальными компонентами: диодами, транзисторами, лампами и т.д. (Если интересно, почему металлические проводники ведут себя подобным образом, читайте §4.4-4.5 отличной книги Перселла и Морриса «Электричество и магнетизм» ) [* См. [8] Приложение _N ] .
Резисторы делаются из какого-либо проводящего материала, например, углеродной массы или металлической плёнки или проволоки из специального сплава. Имеют два контакта и характеризуются сопротивлением: \[ R = V/I. \qquad \qquad \qquad [1.2] \]
\(R\) выражается в омах. Уравнение [1.2] известно как закон Ома. Наиболее распространены металлоплёночные и углеродные резисторы с номиналами от 1 ома ( 1 Ω ) до 10 мегом ( 10 MΩ ) . Кроме того, резисторы нормируются на мощность, которую могут рассеять. Более всего распространены ¼ и ⅛W . В стандартные характеристики также входят: физический размер _7 , точность ( допуск номинала ), температурный коэффициент сопротивления ( ТКС), зависимость от напряжения ( насколько сопротивление меняется при изменении приложенного напряжения ), стабильностью во времени, паразитной индуктивностью и т.д. См. также врезку, Часть X1 [* §X1.2 ] и Приложение _C . На рис. 1.2 показана коллекция резисторов, представляющая большую часть технологий и типов.

Рис. 1.2 Некоторые виды резисторов. Верхний ряд ( проволочные керамические мощные резисторы ) слева направо : 20 W выводной остеклованный, 20 W с винтовым креплением, 30 W остеклованный, 5 и 20 W под винтовой монтаж. Средний ряд ( проволочные мощные резисторы ): 1 , 3 и 5W с аксиальными выводами керамические; 5 , 10 , 25 и 50 W для крепления на теплоотвод ( типа «Dale» ). Нижний ряд : углеродные композитные ( 2 , 1 , ½ , ¼ и ⅛W ); для поверхностного монтажа ( размеры 2010 , 1206 , 0805 , 0603 и 0402 ); наборы резисторов в 6-, 8- и 10-выводных корпусах SIP; набор резисторов в корпусе DIP. Внизу металлоплёночный резистор RN55D ¼W , 1% , два резистора почти в центре - высокоомные Victoreen: стеклянный 2 GΩ и керамический 5 GΩ
Приставки
Эти приставки повсеместно используются для масштабирования единиц в науке и технике. Их происхождение пытаются объяснить несколько версий, имеющих сомнительные исторические обоснования. Приставки ставятся перед именем единицы без пробела и требуют внимательности в использовании заглавных и строчных букв ( особенно плохо дело с «m» и «M» ). Например, 1 mW - милливатт - одна тысячная ватта, 1 MHz - мегагерц - миллион герц. Физические единицы в полной форме пишутся строчными буквами, даже если являются именами учёных. В сокращённой форме единицы, являющиеся именами, пишутся заглавными буквами, поэтому герц и килогерц, но Hz и kHz [* или Генрих Герц] , ватт, милливат и мегаватт, но W , mW и MW [* Вт, мВт, МВт или Джеймс Уатт, а s - это просто секунда ] .
==5
Грубо говоря, резисторы используются для преобразования напряжения в ток и обратно. Звучит довольно шаблонно, но скоро станет понятно, о чём идёт речь.
1.2.2.B Последовательное и параллельное соединение резисторов
Из определения сопротивления следуют несколько выводов.

Рис. 1.4 Последовательное соединение резисторов
-
Сопротивление двух последовательных резисторов ( рис. 1.4 ) равно \[ R = R_1 + R_2. \qquad \qquad \qquad [1.3] \]
Последовательное включение резисторов всегда увеличивает сопротивление.
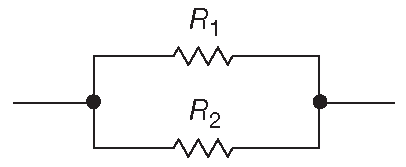
Рис. 1.5 Параллельное соединение резисторов
-
Сопротивление двух параллельных резисторов ( рис. 1.5 ) равно \[ R=\frac{R_lR_2}{R_1 + R_2}=\frac{1}{\frac{1}{R_1}+\frac{1}{R_2}} \qquad [1.4] \]
Параллельное включение резисторов всегда уменьшает сопротивление.
Сопротивление измеряется в омах ( Ω ), но на практике для значений, больших 1000 Ω ( 1 kΩ ), символ «Ω» часто опускают. Таким образом, резистор 4.7 kΩ указывают как 4.7k , а 1 MΩ как 1M _9 . Совсем скоро вся эта куча скучных сведений начнёт использоваться в реальных схемах.
Упражнение 1.1
Имеется резистор 5 kΩ и 10 kΩ . Какое сопротивление будет
(a) у их последовательного и
(b) параллельного соединения?
Упражнение 1.2
Если резистор 1 Ω подключить к 12-вольтовой автомобильной батарее, сколько мощности на нём выделится?
Упражнение 1.3
Докажите формулы для последовательного и параллельного соединения.
Резисторы
Резисторы - самые распространённые электронные компоненты. Их типов почти так же много, как и способов использования. В усилителях резисторы служат нагрузкой для активных элементов, в цепях смещения и обратной связи. На пару с конденсаторами резисторы задают постоянную времени и превращаясь в фильтры. Резисторы устанавливают рабочие точки и уровни сигналов. В источниках питания они ограничивают напряжение, рассеивая избыточную мощность, помогают измерить ток и разрядить накопительные конденсатора. Резисторы устанавливают пропорции напряжений и величины усиления. В логических схемах они используются в качестве шинных терминаторов и подтяжек. В высоковольтных схемах используются для изменения напряжения и выравнивания потенциалов вдоль цепочки диодов или конденсаторов. В радиочастотных устройствах резисторы задают добротность резонансных контуров и даже служат каркасами для катушек индуктивности.
Выпускаются резисторы с номиналами от 0.0002 Ω до 1 TΩ , стандартные мощности от ⅛ до 250 W , точность от 0.005 до 20% . Резисторы делают по металлоплёночной, металл-оксидной, углеродной композитной и керамической композитной технологии, из металлической фольги и металлической проволоки и даже из полупроводниковых материалов в виде структуры, напоминающей полевой транзистор. Чаще всего используют три первых варианта. Резисторы упаковывают в цилиндрические корпуса с аксиальными выводами ( к таковым относятся металлоплёночные RN55D 1% ¼W ) _8 или в виде гораздо более компактных «чип-резисторов» в корпусах для поверхностного монтажа. Стандартные представители имеют точность 5 , 2 и 1% и номинал в диапазоне от 1 Ω до 10 MΩ . 1%-номиналы имеют 96 значений на декаду, 2% - 48 , а 5% - 24 ( см. Приложение _C ). Самые распространённые корпуса показаны на рис. 1.2 .
Резисторы столь просты и очевидны в использовании, что на них часто не обращают внимание. Но, как и прочие компоненты, резисторы не совершенны, и об их ограничениях следует знать, чтобы такие ограничения не стали однажды неприятным сюрпризом. Основными недостатками являются изменения сопротивления от температуры, напряжения, времени и влажности. На высоких частотах начинает влиять индуктивность, а рассеиваемое тепло и электрический шум будут влиять на точные малосигнальные цепи. Тема развивается в Части X1 [* см. §X1.2 ] .
==6
Упражнение 1.4
Покажите, что несколько резисторов, включённых параллельно, имеют сопротивление
\[
R = \frac{1}{\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+...} \qquad \qquad [1.5]
\]
Новички стараются увильнуть от изучения сложных формул при выяснении принципов работы схем. Для таких случаев есть несколько удобных интуитивных приёмов и правил.
- #1
- Резистор большого номинала и малого, включённые последовательно ( параллельно ), дадут сопротивление, немного отличающееся от большего ( меньшего ) номинала. Таким образом, можно «подстраивать» номинал до нужного. Чтобы поднять сопротивление надо взять ближайшее снизу значение и выбрать разницу, добавив небольшой последовательный резистор. Чтобы уменьшить сопротивление надо взять ближайшее сверху значение и поставить параллельно гораздо больший номинал. В последнем случае полезно ориентироваться на пропорции: чтобы снизить значение на 1% надо поставить параллельно резистор с номиналом, в 100 раз большим, чем исходный 10 .
- #2
- Предположим, требуется оценить сопротивление параллельного соединения резисторов 5 kΩ и 10 kΩ . Если рассматривать 5 kΩ как параллельное соединение двух резисторов 10 kΩ , то итоговая схема будет выглядеть как параллельное соединение из трёх резисторов 10 kΩ . Т.к. сопротивление N параллельных резисторов равно 1/N исходного номинала, ответ задачи будет - 10 kΩ/3 или 3.33 kΩ . Это очень полезный приём, который позволяет оценивать схему в уме, без дополнительных расчётов. Авторы рекомендуют развивать проектирование в уме или «на салфетках», хотя бы для первичной проверки идеи.
Ещё немного доморощенной философии. Новички часто считают номиналы и величины с большим числом цифр после запятой, благо калькуляторы и компьютеры это позволяют. Есть две причины избегать таких привычек.
- Компоненты имеют вполне конкретную точность ( типичные значения для резисторов - ±5% , и ±1% , для конденсаторов - ±10% или ±5% , а параметры транзисторов могут отличаться в разы ).
- Признаком хорошей схемы является нечувствительность к разбросу номиналов компонентов ( из этого наблюдения, естественно, есть исключения ).
Навык интуитивного анализа разовьётся быстрее, если взять за правило выполнение прикидочных расчётов в уме, а не рассматривать абстрактные символы, появляющиеся на дисплее калькулятора. Авторы твёрдо уверены, что слишком раннее начало изучения электроники с использованием формул и уравнений - надёжный путь для потери понимания реального хода событий.
В попытке создать более понятную модель сопротивления была придумана концепция проводимости G=1/\(R\) . Ток через устройство с проводимостью \( G\) , к которому приложено напряжение \( V \) , определяется формулой: \(I=GV\) ( закон Ома ). Небольшое сопротивление означает большую проводимость, а значит, больший ток при том же напряжении. В таком свете формула для параллельного соединения резисторов становится очевидной. Когда несколько резисторов ( проводящих путей ) подключаются к одним и тем же потенциалам, значит, общий ток будет суммой токов индивидуальных путей. Отсюда, общая проводимость является суммой проводимостей \( G=G_1+G_2+..\) . Таким образом, получили ту же формулу для параллельного соединения, что и ранее.
Инженеры горазды придумывать обратные единицы. Для проводимости был выбран «сименс» ( S=1/Ω ). Раньше эту обязанность исполнял «мо» ( «Ом», прочитанный задом наперёд, а его символом служил перевёрнутый вверх ногами знак ома «℧» ). Проводимость облегчает анализ, но широкого применения не нашла 11 : большинство людей продолжает думать в терминах сопротивления.
1.2.2.C Мощность и резисторы
Мощность, рассеиваемая резистором ( или любым другим устройством ) равна \( P=IV\) . С помощью закона Ома можно написать эквивалентные формы \( P=I^2R = U^2/R\) .
Упражнение 1.5
Покажите, что в схеме с питанием 15 V для резистора номиналом более 1 kΩ невозможно превысить мощность ¼W , независимо от способа включения.
Упражнение 1.6 (Дополнительное упражнение ).
Городу Нью-Йорк требуется примерно 1010 ватт электрической мощности при 115 V 12 ( вполне разумная цифра: 10 миллионов жителей, 1kW на каждого ). Подсчитайте, что получится, если попробовать передать эту мощность через кабель из чистой меди диаметром 1 фут ( 30 cm ). Сопротивление такого кабеля 0.05 μΩ ( 5·10-8Ω ) на 1 фут длины. Надо подсчитать:
(a) потери мощности на фут длины ( их называют «потери I2R» или «потери в меди» ),
(b) длину кабеля, на которой будут потеряны все 1010 ватт,
(c) на сколько градусов нагреется кабель, если σ=6×10-12W/(K4cm2) .
Если расчёты будут выполнены правильно, результат вас удивит. Как можно разрешить эту техническую проблему?
==7
1.2.2.D Входы и выходы
Практически все электронные схемы имеют вход какого-либо вида ( обычно речь идёт о напряжении ) и создаёт соответствующее выходное действие ( опять же, обычно меняет напряжение ). Например, звуковой усилитель может создавать на выходе меняющееся напряжение, в 100 раз большее, чем меняющееся таким же образом входное напряжение. Читая такие описания, можно вообразить измерение выходного напряжения для заданного входного, но в инженерной среде принято говорить о функции передачи \(\mathbf{H}\) - отношении измеренного выходной реакции к поданному на вход воздействию. [* Т.е. отталкиваться от выходного сигнала. Кстати, легко заметить, что определение никак не оговаривает ни вид входного воздействия ( ток, напряжение, звук, тепло.. ), ни выходную реакцию ( напряжение, обороты двигателя и т.д. ), причём функция не обязана оперировать действительными числами ] . Для упомянутого усилителя \(\mathbf{H}\) - просто константа ( \(\mathbf{H}\)=100 ) . Усилители появятся в Части _2 , а сейчас будет разобран очень важный элемент электронных схем, состоящий из одних резисторов, - делитель напряжения .
1.2.3 Делитель напряжения
Мы подошли к делителю напряжения - одному из самых распространённых элементов электронных схем. Загляните в какое-нибудь рабочее устройство, и в нём немедленно обнаружится десяток делителей напряжения. Делитель - это схема, которая передаёт на выход точно известную часть входного напряжения. Самый простой делитель показан на рис. 1.6 .
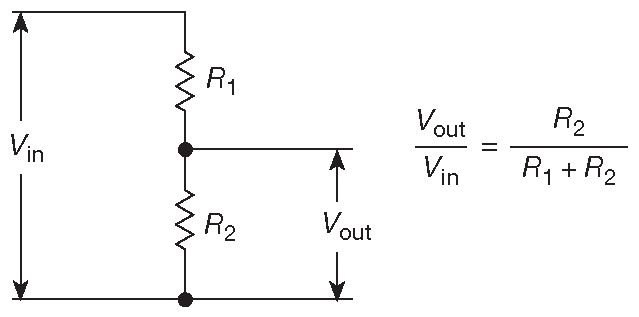
Рис. 1.6 Делитель напряжения. Входное напряжение \( V_{in}\) является источником для меньшего по величине выходного напряжения \( V_{out}\)
Некоторые пояснения. При изображении схем в общем случае предполагается, что \( V_{in}\) слева на схеме - напряжение, подаваемое на её вход, а \( V_{out}\) справа - результирующее выходное напряжение, создание которого и есть задача схемы. Предполагается, что читатель всё это уже знает, потому что:
- «слева направо» - общепринятая практика рассмотрения сигналов,
- у сигналов «говорящие» имена ( \( V_{in}\) , \( V_{out}\) ) и
- другие схемы нарисованы так же.
Это может немного смущать поначалу, но потом воспринимается естественно.
Чему равно \( V_{out}?\) Предполагаем, что нагрузка отсутствует, т.е. к выходным клеммам ничего не подсоединено. Тогда ток во всех точках схемы одинаковый \[ I=\frac{V_{in}}{R_1+R_2} \] ( использовалось соотношение для последовательного соединения и закон Ома ). Тогда для \(R_2:\) \[ V_{out} = I·R_2 = V_{in}·\frac{R_2}{R_1+R_2}. \qquad \qquad [1.6] \]
Отметим, что выходное напряжение всегда меньше ( или равно ) входному. Именно поэтому схема называется делителем. Получить усиление ( выходное напряжение, превышающее входное ) можно, если одно из сопротивлений отрицательное. Идея не так безумна, как кажется на первый взгляд. Создать схему с отрицательным сопротивлением для малого сигнала можно. Есть, например, компонент - туннельный диод . Можно сделать даже «настоящее» отрицательное сопротивление - преобразователь с отрицательным сопротивлением ( о нём будет речь в §6.2.4.B ), но это узкоспециальное устройство, которое сейчас изучать рано.
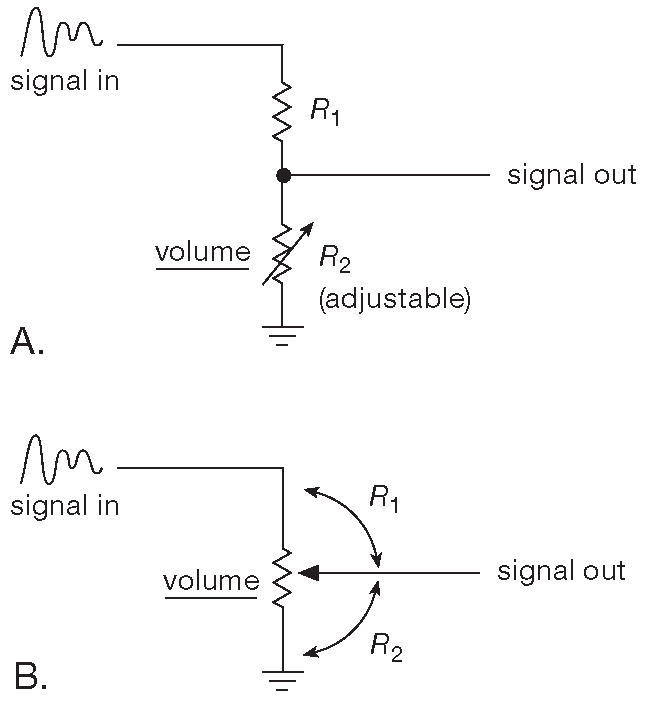
Рис. 1.7 Подстраиваемый делитель напряжения можно сделать из постоянного и переменного резистора или из потенциометра. В некоторых современных устройствах можно найти длинную цепочку резисторов одного номинала, снабжённых электронными ключами, которые позволяют выбрать любое соединение между резисторами и подключить его к выходу. Достаточно сложная схема, зато она позволяет производить подстройку напряжения электрическим сигналом , а не механическим воздействием
Делители напряжения часто используют в схемах, требующих конкретной части от какого-то опорного напряжения, которое может быть и переменным. Например, если \( V_{in}\) - меняющееся напряжение, а \(R_2\) - переменный резистор ( рис. 1.7A ), то получается «регулятор громкости». Более простой вариант получается, если \(R_1R_2\) образуют единый переменный резистор - потенциометр ( рис. 1.7B ). Эта конструкция очень распространена, а потенциометры выпускаются самых разных видов и стилей, некоторые из которых можно посмотреть на рис. 1.8 .

Рис. 1.8 Потенциометры. Верхний ряд слева направо ( варианты для монтажа на панель ): мощный проволочный, 2-ваттный углеродный композитный типа AB, 10-оборотный проволочный, сдвоенный. Средний ряд ( для монтажа на панель ): оптический энкодер без ограничения угла ( 128 импульсов на оборот ), однооборотный керамический композитный, однооборотный углеродный, подстроечный однооборотный под шлиц с фиксацией. Передний ряд ( подстроечные для монтажа на плату ): многооборотный с боковым расположением вала ( два вида ), счетверённый однооборотный, квадратный ⅜" ( 9.8 mm ) однооборотный, квадратный ¼" ( 6.4 mm ) однооборотный, круглый ¼" ( 6.4 mm ) однооборотный, квадратный 4 mm однооборотный для поверхностного монтажа, квадратный 4 mm многооборотный для поверхностного монтажа, квадратный ⅜" ( 9.5 mm ) многооборотный, счётверённый 256-уровневый электронный резистор ( EEPOT ) в 24-ногом корпусе
==8
Простой делитель может быть полезен как способ рассмотрения схем. Входное напряжение и верхний резистор могут представлять выходной сигнал и импеданс первого каскада, а нижний резистор - входной импеданс следующего каскада [* см. рис. 2.15 ] . В таком случае уравнения, описывающие делитель, скажут, какое напряжение увидит второй каскад. Идея станет понятнее, после знакомства с теоремой Тевенина ( §1.2.5 ), а сейчас несколько слов об источниках напряжения и тока.
==8
2 Это определения , но вряд ли инженеры думают о напряжении в таком ключе. Со временем любой разработчик начинает понимать, что такое напряжение в применении к электронным схемам. Грубо ( очень грубо ) говоря, напряжение - это то, что заставляет течь ток. <-
3 Можно сказать, что инженеры других специальностей завидуют разработчикам электроники, имеющим столь замечательное средство отображения. <-
4 В области высоких частот и заметных токов это утверждение не вполне соответствует действительности, о чём говорится позднее в Части X1 [* §X1.1 ] , но на данный момент это будет хорошим приближением. <-
5 Если, конечно, вы не работаете с силовым электрическим оборудованием, вроде линейных трансформаторов на 13 kV и т.п. Этим ребятам можно говорить «ампераж». <-
6 ...и ещё, «оммаж» - это тоже неправильно, сопротивление , пожалуйста. <-
7 Размеры чип-резисторов и прочих компонентов, предназначенных для монтажа на поверхность, обозначаются четырёхзначным кодом, соответствующим геометрическим размерам корпуса. Например, резистор 0805 имеет размер 80×50 mil ( 1 mil=0.001") или 2×1.25 mm . Высота, если требуется, указывается отдельно. Чтобы внести разнообразие в эту скучную схему, размеры могут указываться в метрической системе , причём без упоминания данного факта. В ней цифры указывают в десятых долях миллиметра, поэтому дюймовый 0805 превращается в метрический 2012 . <-
8 Эти резисторы нормируются как RN55 ⅛W по военному стандарту (“MIL-spec”), но как CMF-55 ¼W по обычному промышленному. <-
9 Популярная «международная» [* и, кстати, гораздо более удобная] нотация заменяет десятичную точку символом множителя, например, 4k7 , 1M0 . Резистор 2.2 Ω превращается в 2R2 [* или 2E2 , вероятно, E меньше похоже на прочие множители номинала ] . Аналогичные принципы действуют для емкостей и индуктивностей. <-
10 Ошибка составит около 0.01% . <-
11 И только теорема Миллмана использует данную концепцию. Она гласит, что выходное напряжение набора резисторов ( назовём их \(R_i\) ) , соединённых на выходной стороне, к которым подведены какие-то напряжения ( \( V_i\) ) , составит \( V_{out}=(Σ V_iG_i/Σ G_i\) ) , где \( G_i\) - проводимости резисторов ( \( G_i=1/R_i\) ) . <-
12
«Официальное» значение напряжения 120 V±5\% , но в сети можно увидеть и 110 V, и 115 V, и 117 V. Такая неточность ( 115 V ) вполне допустима ( и используется в книге ), потому что
(a) при подключении потребителя значение напряжения в стенной розетке понижается на несколько вольт, и
(b) минимальное допустимое напряжение равно 110 V. См. стандарт ANSI C84.1.
<-

