1.3 Сигналы
==13
Дальше в данной части говорится о конденсаторах - компонентах, чьи параметры зависят от характера изменения токов и напряжений в схеме. Анализ на постоянном токе, применявшийся до настоящего момента ( закон Ома, эквивалентное преобразование Тевенина и т.д. ), работает по-прежнему, притом даже, что напряжения и токи меняются во времени. Но чтобы правильно понимать, что происходит в схеме на переменном токе ( ac ), полезно держать в голове параметры некоторых общеупотребительных сигналов , амплитуды которых меняются во времени определённым образом.
==14
1.3.1 Синусоидальные сигналы
Синусоида - самый распространённый вид сигналов. Её можно найти в стенной розетке. Если кто-то говорит: «Подайте сигнал 10 μV частотой 10 MHz», то имеется в виду синусоидальный сигнал. Это напряжение, описываемое уравнением \[ V=A\sin( 2 π ft ) \qquad \qquad \qquad [1.10] \] где A называется амплитудой, а \( f \) - частотой в герцах ( циклах в секунду ). Синусоидальный сигнал выглядит как волна на рис. 1.19 . Иногда важно знать, какое значение у него было в момент t=0 и в этом случае в уравнении может появиться фаза φ : \[ V=A\sin( 2 π ft+ φ) \]
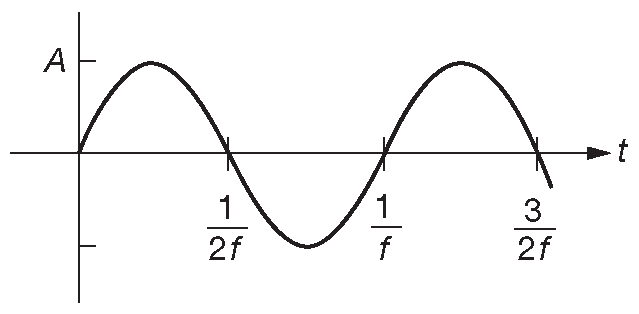
Рис. 1.19 Синусоидальный сигнал с амплитудой A и частотой f
Ещё одним вариантом описания является выражение для угловой частоты \[ V=A\sin (ω t ). \]
Здесь \(ω\) - угловая частота, измеряемая в радианах в секунду. Чтобы не ошибаться, надо всего-то запомнить простое соотношение \(ω=2πf\) .
Основным достоинством синусоидальных сигналов ( и причина их неизменной популярности ) является то, что уравнение синусоиды является решением линейных дифференциальных уравнений, описывающих многие природные явления и свойства линейных схем. Линейные схемы характеризуются тем, что реакция от суммы сигналов на входе будет эквивалентна сумме реакций, получающихся для каждого отдельного сигнала из суммы. Таким образом, если \(\mathscr F( A\) ) представляет выходной сигнал, полученный из входного сигнала A , то схема считается линейной, если \(\mathscr F( A+B )=\mathscr F(A)+\mathscr F( B\) ) . Линейная схема, получающая на входе синусоиду, всегда выдаёт на выход синусоиду, хотя, возможно, амплитуда и фаза изменятся. Другие периодические сигналы таким свойством похвастаться не могут. Описание параметров схемы через её частотный отклик [* т.е. АЧХ] является стандартной практикой. Под частотным откликом понимается характер изменения амплитуды приложенного к схеме синусоидального напряжения, при изменении его частоты. Скажем, стерео усилители должны иметь «плоскую» частотную характеристику как минимум в полосе частот 20 Hz...20 kHz .
Обычно приходится иметь дело с синусоидальными сигналами из диапазона от нескольких герц до нескольких десятков мегагерц. Низкие частоты вплоть до 0.0001 Hz можно получить, если аккуратно собрать нужную схему. Частоты до 2000 MHz ( 2 GHz) требуют использования согласованных линий передачи. На более высоких частотах обычные электронные схемы перестают работать, и требуются специальные приёмы проектирования.
1.3.2 Амплитуда и децибелы
Есть и иные, отличные от указания амплитуды, способы описания синусоидальных и некоторых других сигналов. Иногда можно встретить размах сигнала - амплитуду от пика до пика , которая является именно тем, о чём говорит - удвоенной амплитудой. Ещё одним способом является указание среднеквадратической амплитуды ( rms ): \( Vrms \)=(1/\(\sqrt2\))A=0.707A . Такое описание подходит только для синусоидальных сигналов. Для напряжений иной формы соотношение pp-rms будет другим. Несмотря на несколько странное представление это обычный метод, т.к. rms напряжение используется для расчёта мощности. Номинальное напряжение в розетке на стене для США 120 Vrms@60 Hz , амплитуда 170 V ( 339 Vpp ) 18 .
==15
1.3.2.A Децибелы
Как можно сравнить амплитуды двух сигналов? Можно сказать, что «X» в два раза больше, чем «Y». Это будет правильно и во многих случаях удобно, но в электронике часто приходится иметь дело с отношениями, исчисляемыми миллионами, поэтому логарифмические измерения были бы удобнее. Единицей для таких измерений служит децибел - одна десятая бела, который никто никогда не использует. По определению отношение двух сигналов в децибелах вычисляется по формуле: \[ dB=10·\lg\left(\frac{P_2}{P_1}\right ), \qquad \qquad \qquad [1.11] \] где \( P_1\) и \( P_2\) - мощности двух сигналов. Часто приходится иметь дело с амплитудами , и для них отношение чуть меняется: \[ dB=20·\lg\left(\frac{A_2}{A_1}\right ), \qquad \qquad \qquad [1.12] \] где \( A_1\) и \( A_2\) - амплитуды двух сигналов. Например, если один сигнал в два раза больше другого, то это +6 dB , т.к. \(\lg2\)=0.3010 . Если разница 10× , то это +20 dB в большую сторону и –20 dB в меньшую.
[* А откуда берётся коэффициент 2 ?
Электрическая мощность равна \( P=IV\) или \( P=V^2/R\) . Тогда
\[
dB=10·\lg\left(\frac{P_2}{P_1}\right )= 10·\lg\left(\frac{V_2^2/R_2}{V_1^2/R_1}\right )= 10·\lg\left(\frac{V_2^2}{V_1^2}\right ) =10·\lg\left(\frac{V_2}{V_1}\right )^2 =10·2·\lg\left(\frac{V_2}{V_1}\right ).
\]
А почему \(R_1\) и \(R_2\) сократились?
Потому что они одинаковые, иначе невозможно сравнивать величины, т.к. мощность может зависеть от сопротивления нагрузки ( см. §1.2.5.B ). Скажем, для радиочастот \(R_1=R_2\) = 50 Ω ] .
Исходно децибелы использовались для указания отношения двух сигналов, но иногда подразумевается некоторый опорный источник, и амплитуда указывается относительно него. Существует несколько стандартных уровней ( которые не стандартизованы, но вполне очевидны ), используемых подобным образом. Вот список популярных вариантов.
- 0 dBV : относительно уровня 1 Vrms .
- 0 dBm : напряжение, соответствующее мощности 1 mW на некотором очевидном импедансе нагрузки. Для радиочастотных схем это 50 Ω , а для аудиотехники - 600 Ω . Соответствующие амплитуды составляют 0.22 Vrms и 0.78 Vrms .
- Шумовой сигнал, создаваемый резистором при комнатной температуре ( этот необычный факт обсуждается в §8.1.1 ).
Помимо перечисленных, есть и иные стандартные уровни, используемые в других областях инженерного дела и науки.
- Скажем в акустике принят уровень 0 dB SPL . Это звуковая волна, создающая давление 20 μPa ( \( 2×10^{-10}\)atm).
- В электросвязи уровень можно отсчитывать в dBrnC ( относительный уровень шума взвешенный по частоте в соответствии с «кривой C» ).
Когда амплитуда указывается подобным образом, надо, чтобы уровень 0 dB обладал какими-то особыми свойствами, скажем, это уровень «+27 децибел относительно 1 Vrms», он же «27 dB re 1Vrms», либо задать единицу «dBV» 19 .
Упражнение 1.12
Определите разницу амплитуд и мощностей для пары сигналов со следующими отношениями:
(a) 3 dB , (b) 6 dB , (c) 10 dB , (d) 20 dB .
Упражнение 1.13
Это упражнение можно назвать «децибелами пустынного острова». В таблицу ниже внесены некоторые цифры отношений мощностей из предыдущего упражнения. Задача - заполнить таблицу до конца, используя только бумагу и карандаш.
Возможно, будет полезна следующая подсказка. Надо начать с 10 dB и идти вниз по таблице с шагом 3 dB , а затем вверх на 10 dB , затем опять вниз. Наконец, разберитесь с некруглым числом 3.125 ( и его ближайшим окружением ), которое довольно близко к π .
1.3.3 Прочие сигналы
1.3.3.A Линейно меняющийся
Линейно меняющийся сигнал похож на рис. 1.20 A . Это просто амплитуда возрастающая ( или снижающаяся ) с постоянной скоростью. Вести себя подобным образом бесконечно невозможно даже в фантастическом фильме, поэтому в жизни такой сигнал аппроксимируется ростом до определённого уровня ( рис. 1.20B ) или периодическим сигналом, известным как «пилообразный» ( рис. 1.20C ).
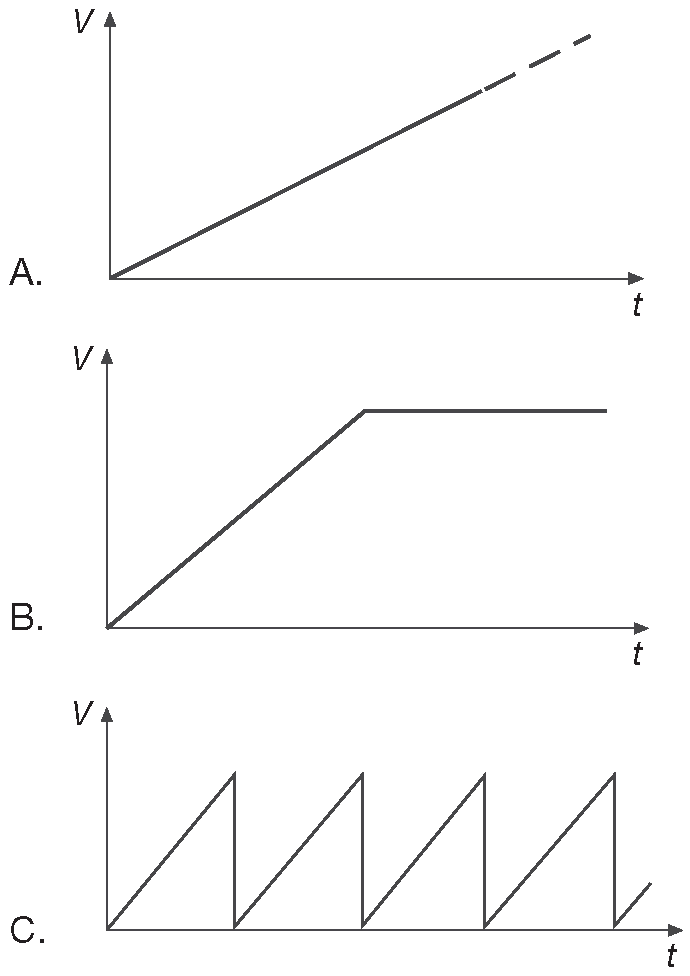
Рис. 1.20 (A) Линейно меняющийся сигнал. (B) Линейно меняющийся сигнал с ограничением. (C) Пилообразный сигнал
1.3.3.B Треугольник
Треугольник очень похож на линейно возрастающий. Это просто симметричный линейный сигнал ( рис. 1.21 ).
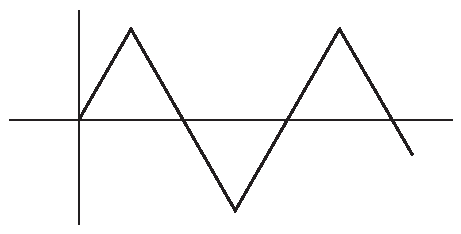
Рис. 1.21 Треугольный сигнал
1.3.3.C Шум
==16
Нужные сигналы часто перемешаны с шумом . Это всеобъемлющий термин, который чаще всего применяют к случайному тепловому шуму. Шумовое напряжение может быть задано частотным спектром ( мощностью на герц ) или распределением амплитуд. Один из самых распространённых видов шума - ограниченный по полосе белый гауссов шум . Основное его достоинство - одинаковая мощность, приходящаяся на герц в некоторой полосе частот и гауссово ( в виде колокола ) распределение амплитуд. Эти амплитуды можно наблюдать, если проводить мгновенные измерения уровня в течение какого-то времени [*] . Такой шум создаёт резистор ( джонсоновский , он же тепловой, он же шум Найквиста ). Мешает точным измерениям любого вида. Примерная картинка с осциллографа представлена на рис. 1.22 . Шум и способы построения малошумящих схем подробно рассматриваются в Части _8 .
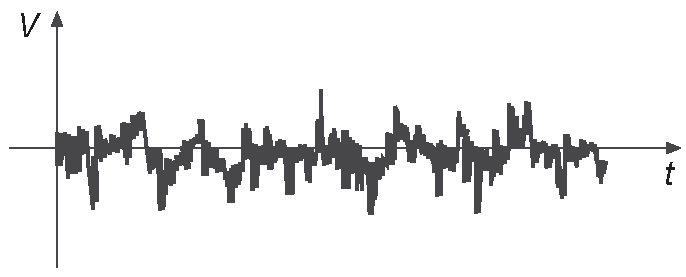
Рис. 1.22 Шум
[*]
[* Т.е. берём белый шум, ограничиваем его полосу ( пропускаем через полосовой фильтр ) и проводим измерения амплитуд в течение некоторого времени ( §8.13 ). Получаем при этом набор чисел, которые ложатся на картинку 8.2 ( по горизонтали - амплитуда, по вертикали - вероятность появления )]
1.3.3.D Прямоугольный сигнал
Прямоугольный сигнал показан на рис. 1.23 . Подобно синусоидальному, он описывается амплитудой, частотой и иногда фазой. Линейные схемы, получающие на входе прямоугольный сигнал, редко отвечают таким же сигналом на выходе. [* Объяснения этому факту в Части _4 и _6 ] . Для прямоугольного сигнала среднеквадратическая и пиковая амплитуды совпадают.
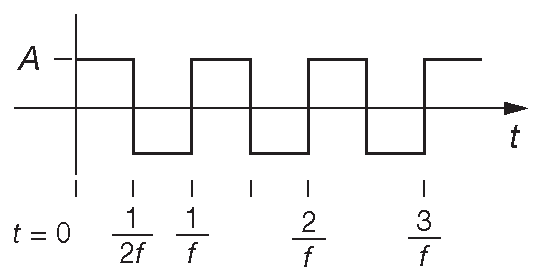
Рис. 1.23 Прямоугольный сигнал
Края прямоугольного сигнала не являются идеально прямоугольными. В типичных электронных схемах время нарастания \( t_r\) имеет величину от наносекунд до микросекунд. На рис. 1.24 показано, как это обычно выглядит. Время нарастания определяется как время, проходящее, пока сигнал изменяется от 10% до 90% общей величины перепада.
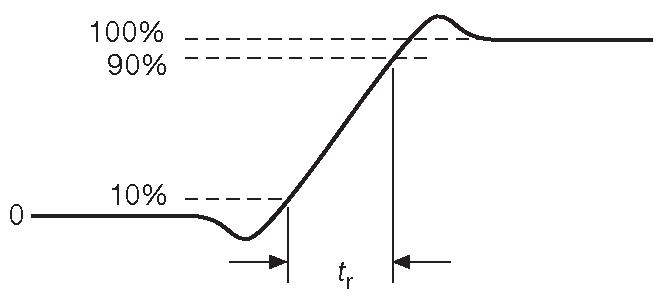
Рис. 1.24 Время нарастания для перепада
1.3.3.E Импульсы
Импульсы - сигналы, напоминающие форму с рис. 1.25 . Они характеризуются амплитудой и шириной импульса. Можно создать последовательность импульсов, идущих с равными интервалами ( периодических ). В этом случае принято говорить о частоте следования или повторения и о «скважности» - об отношении ширины [* активной части ] импульса к периоду повторения. Цифра может меняться от 0 до 100% . Импульсы могут быть положительной и отрицательной полярности и, кроме того, могут быть «положительными» и «отрицательными» . Скажем, второй импульс на рис. 1.25 - отрицательный импульс положительной полярности.
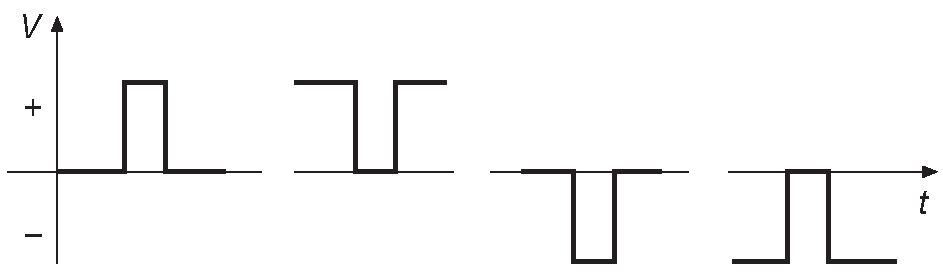
Рис. 1.25 Положительные и отрицательные импульсы обеих полярностей
==17
1.3.3.F Перепады и иголки
Перепады и иголки ( рис. 1.26 ) часто упоминаются, но нечасто используются. Они удобны при описании происходящих в схеме процессов. Перепад - часть прямоугольного сигнала, а иголка - скачок уровня с очень малой длительностью.
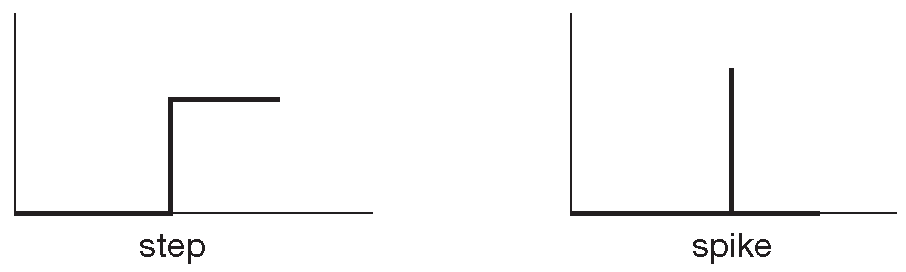
Рис. 1.26 Перепад и иголка
1.3.4 Логические уровни
Импульсы и прямоугольные сигналы активно используются в цифровой электронике, в которой два заданных уровня напряжения представляют два возможных состояния, единственно допустимых для любой точки схемы. Такие состояния просто зовут ВЫСОКОЕ и НИЗКОЕ. Они могут представлять нули и единицы булевой алгебры ( алгебры логики ).
Цифровой электронике не требуется высокая точность потенциалов. Её задача - просто различать два состояния. Каждое логическое семейство задаёт свою пару уровней для ВЫСОКОГО и НИЗКОГО состояния. Например, семейство 74LVC’ работает при +3.3 V и имеет выходные уровни 0V (НИЗКИЙ ) и +3.3 V ( ВЫСОКИЙ ). Порог переключения между этими состояниями ∼1.5 V . На самом деле входной сигнал НИЗКОГО уровня может иметь величину 0.4 V , это не скажется на работе схемы. Цифровая логика рассматривается в Частях 10 , 11 , 12 .
1.3.5 Источники сигналов
Источником сигнала обычно является одна из частей проектируемой схемы, но при отладке универсальный источник тестовых сигналов незаменим. Бывают такие источники трёх видов: генераторы сигналов, генераторы импульсов и генераторы функций.
1.3.5.A Генераторы сигналов
Генераторы сигналов - источники синусоидальных сигналов, имеющие широкие возможности по перестройке частоты и точному контролю амплитуды. Для последней задачи прибор снабжается аттенюатором - набором переключаемых резистивных делителей. Некоторые модели позволяют модулировать выходной сигнал, т.е. менять его по времени. Если речь идёт об амплитуде, то говорят об «амплитудной модуляции» ( “AM” ), а, если о частоте, то о «частотной» ( “FM” ). Вариантом данной схемы является генератор качающейся частоты - прибор, позволяющий периодически плавно изменять выходную частоту в некоторых пределах. Такие генераторы нужны для тестирования схем, чьё поведение зависит от частоты определённым образом, например, фильтров. [* Так-то от частоты зависит поведение любой схемы] . В настоящее время такие приборы, и вообще измерительное оборудование позволяет задавать параметры ( частоту, амплитуду и т.д. ) с помощью компьютера.
Для многих генераторов исходным сигналом служит синусоидальное напряжение, частота которого устанавливается в цифровой форме с точностью до восьми и более десятичных разрядов. Этим занят синтезатор частоты , но для работы ему требуется очень точный опорный источник - кварцевый резонатор, рубидиевый стандарт или приёмник GPS. Подробности этой схемы описываются в §13.13.6 . Типичным синтезатором является прибор SG384 фирмы Stanford Research Systems. Он позволяет получить сигнал в диапазоне частот от 1 μHz до 4GHz с амплитудой от –110 dBm до +16.5 dBm ( от 0.7 μV до 1.5 Vrms ) и амплитудной, фазовой или частотной модуляцией. Стоит около $4600. Можно приобрести программируемый генератор частоты, а можно и программируемый генератор сигналов произвольной формы - генератор функций , но, если требуется высокая точность установки частоты синусоидальных сигналов, синтезаторам нет равных.
1.3.5.B Генераторы импульсов
Генераторы импульсов могут создавать только импульсы, но зато какие! Можно менять ширину, частоту повторения, амплитуду, полярность, время фронта и т.д. Самые быстрые модели позволяют получить гигагерцовую частоту следования. Такие приборы могут выдавать два импульса с настраиваемыми временными параметрами пары или даже программировать сложную серию сигналов ( генератор испытательных сигналов ). Большая часть современных приборов позволяет задать логические уровни выходного сигнала для упрощения сопряжения с цифровыми схемами и задавать все настройки программно.
1.3.5.C Генераторы функций
Генераторы функций - наиболее универсальный вариант источника сигналов. Он позволяет создавать синусоидальные, треугольные и прямоугольные сигналы в очень широком диапазоне частот ( типичный диапазон - от 0.01 Hz до 30 MHz ) с точным заданием амплитуды и постоянного смещения ( постоянный уровень, который прибавляется к сигналу. Многие позволяют задавать качание частоты и характер её изменения ( линейный, логарифмический ). У них есть импульсный режим работы, хотя и не столь гибко настраиваемый. Некоторые позволяют использовать внешний модулирующий сигнал.
==18
Прежние генераторы функций были по большей части аналоговыми, но современные модели насквозь цифровые, позволяющие получить одновременно и гибкость настроек, и стабильность вместе с точностью частоты. Кроме того, они позволяют задать произвольную форму периодического сигнала, устанавливая значение амплитуды для набора равноотстоящих моментов времени. Примером может служить Tektronix AFG3102 с нижней границей частоты 1 микрогерц , позволяющий получить синус и прямоугольник с частотой до 100 MHz , импульсы, «шум» и «произвольный» сигнал ( длина последовательности до 128k точек ) до 50 MHz . Имеет пять видов модуляции, качание ( линейное и логарифмическое ) и режим пачек импульсов ( от 1 до 106 ). Настраивать можно всё: частоту, ширину импульсов, время нарастания, модуляцию, амплитуду ( от 20 mV до 10 V ). В нём есть даже весьма необычные виды сигналов: sinc ( \(\sin(x)/x\) ) , экспоненциальный рост и спад, Гаусс и Лоренц. Два независимых выхода и цена в районе $5k. Если хочется иметь один источник сигналов общего применения, то это тот самый прибор.
==18
18 Иногда можно обнаружить устройство ( например, стрелочные измерительные головки ), которые показывают среднюю амплитуду сигнала переменного тока. Для синусоидальных сигналов соотношение \( Vavg=Vrms/1.11\) . Но такие приборы обычно калибруют так, чтобы они показывали среднеквадратичную амплитуду. Для сигналов другой формы отсчёт будет неверен, и для них потребуется «честный среднеквадратический» измеритель. <-
19 Один из авторов, будучи спрошен нетехнической супругой о потраченных на покупку деньгах, ответил: «36 dB$». [* Надеюсь, он получил заслуженный скандал? ] <-

