8.1 «Шум»
==473
Почти в каждой области, где ведутся измерения, предел обнаружения слабых сигналов устанавливается шумом - нежелательным сигналом, который маскирует требуемый. Даже если измеряемая величина достаточно велика, наличие шума снижает точность измерения. Некоторых видов шума избежать нельзя, например, непрерывные изменения самой измеряемой величины ), и их можно отделить методами усреднения сигнала или сужения полосы измерения _3 . Другие формы шума ( радиочастотная интерференция и шум в контуре земли ) можно снизить, применяя специальные приёмы, включающие фильтрацию и работу над взаимным расположением проводов и компонентов. Наконец, существует шум, свойственный самому процессу усиления. Он может быть снижен с помощью специальных методов проектирования аппаратуры. Хотя техника усреднения сигнала часто используется для обнаружения сигнала в шуме, начинать следует с аппаратуры, изначально свободной от интерференции и обладающей самым низким из возможных уровнем шума.
==474
Разговор начнётся с признаков и характеристик разного рода шумов, воздействующих на электронную аппаратуру. После будут рассмотрены шумы биполярных ( БТ - BJT ) и полевых ( ПТ - FET ) транзисторов, методы проектирования малошумящих схем для заданных источников сигнала и приведены некоторые примеры. После короткого обсуждения шумов дифференциальных усилителей и усилителей с обратной связью начнётся рассмотрение приёмов проектирования схем на ОУ, включая трансимпедансные ( ток-в-напряжение ) усилители. Далее раздел об измерении шума, ограничении полосы пропускания и синхронного детектирования , а затем короткий разговор о шумах источников питания. Завершается эта часть изучением методов заземления и экранировки, противодействия электромагнитной интерференции и наводкам.
Термин шум можно отнести ко всему, что маскирует интересующий сигнал _4 . Шум может принимать форму другого сигнала ( «интерференция» ), но чаще этот термин используется для описания случайного сигнала, имеющего физическую ( часто температурную ) природу. Шум можно характеризовать физическим механизмом происхождения, частотным спектром и распределением амплитуд. Рассмотрим основные источники шума.
- Тепловой шум ( Johnson noise ): случайное шумовое напряжение, создаваемое тепловым движением частиц в резистивном элементе.
- Дробовый шум ( Shot noise ): случайный статистический процесс изменений тока, вызванный дискретной природой электрического заряда.
- Фликер шум ( Flicker noise ): дополнительный случайный шум, возникающий вследствие многих причин и проявляющийся на низких частотах, мощность которого пропорциональна 1/\( f \).
- Импульсный шум ( Burst noise ): низкочастотный шум, видимый как случайные переходы между двумя соседними энергетическими уровнями в атомах вещества.
8.1.1 Тепловой шум
Резисторы, даже лежащие на столе, создают на своих выводах шумовое напряжение, известное как тепловой шум ( «джонсоновский» или «Найквиста» ) _5 . Он имеет плоский частотный спектр, т.е. мощность шума, приходящегося на каждый герц частоты, одинакова ( в некотором приближении, конечно ). Шум с плоским спектром распределения называется «белым». Шумовое напряжение, создаваемое резистором \(R\) при температуре T , равно: \[ v_{noise} (rms)=v_n= \sqrt{4kTR×BW} \qquad \mathrm {V(rms)} \qquad \qquad \qquad [8.1] \] где k - Постоянная Больцмана, T - абсолютная температура в Кельвинах ( K=°C+273.16 ) и BW - ширина полосы в герцах. Таким образом, если померить напряжение на резисторе, нагретом до температуры T с помощью идеального свободного от шума полосового фильтра ( с рабочей полосой BW ), то среднеквадратическое напряжение шумов \(v_{noise}\space ( rms\) ) при комнатной температуре ( T=20°C=293K ), то будут получены следующие значения: \[ \begin{align*} 4KT &=1.62 ×10^{-20} & \mathrm {V^2} &/ (\mathrm {Hz·Ω}) \\ \sqrt{4kTR} &=1.27 ×10^{-10}\sqrt{R} & \mathrm {V} &/ \sqrt{\mathrm {Hz}} \\ &=1.27 ×10^{-4}\sqrt{R} & \mathrm {μV} &/ \sqrt{\mathrm {Hz}} \end{align*} \qquad \qquad \qquad [8.2] \]
Например, для 10 kΩ при комнатной температуре в полосе 10 kHz напряжение теплового шума составит 1.3 μV , т.е. именно такое напряжение получится, если подключить резистор ко входу очень хорошего звукового усилителя, и померить выход усилителя вольтметром. Источником указанного шумового напряжения является само сопротивление \(R\) . Если перемкнуть выводы резистора между собой, в получившейся цепи потечёт ток ( короткого замыкания ): \[ i_{noise}\space (rms) = v_{noise}\space (rms)/R = v_{nR}/R = \sqrt{4kT×BW/R} \quad \quad [8.3] \]
Как будет видно из §8.2.1 удобно представлять шумовое напряжение ( или ток ) как плотность \(e_n\) ( среднеквадратическое напряжение, отнесённое к квадратному корню из рабочей полосы ). Тепловой шум с плоским спектром ( белый ) имеет постоянную плотность: \[ e_n=\sqrt{4kTR} \qquad \qquad \mathrm {V/\sqrt{Hz}} \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.4] \] откуда среднеквадратическое напряжение в некоторой ограниченной полосе \( BW\) равно \(v_n=e_n\sqrt{BW}\) . Аналогично, плотность тока короткого замыкания равна \[ i_n=\sqrt{4kT/R} \qquad \qquad \mathrm{A/\sqrt{Hz}} \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.5] \]
На рис. 8.1 приведена зависимость плотности напряжения теплового шума от сопротивления источника и плотности тока короткого замыкания. Удобно запомнить, что при комнатной температуре резистор номиналом 1 kΩ создаёт шумовое напряжение плотностью 4 nV/\(\sqrt{Hz}\) . Для других напряжений это значение надо умножить на квадратный корень из сопротивления [* правильно: «корень из отношения сопротивлений», см. пояснение в §8.13.6 ] _6 .
==475
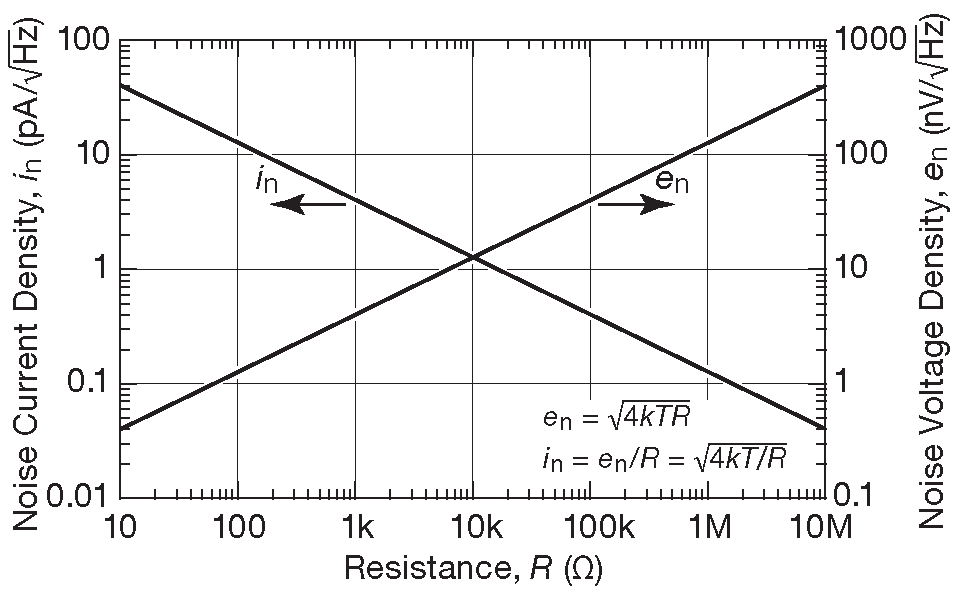
Рис.8.1 Плотность напряжения и тока короткого замыкания теплового шума при температуре 25°C
Приведём небольшую и удобную таблицу шумовых напряжений и токов в полосе 10 kHz и их плотностей, т.е. значений размерности nV/\(\sqrt{Hz}\) и pA/\(\sqrt{Hz}\) для семи декад сопротивлений.
| Сопротивление | разрыв | короткое замыкание | ||
| \(e_n\) | \(e_n\sqrt{BW}\) | \(i_n\) | \(i_n\sqrt{BW}\) | |
| nV/\(\sqrt{Hz}\) | μV | pA/\(\sqrt{Hz}\) | pA | |
| 100 Ω | 1.28 | 0.128 | 12.8 | 1280 |
|---|---|---|---|---|
| 1 kΩ | 4.06 | 0.406 | 4.06 | 406 |
| 10 kΩ | 12.8 | 1.28 | 1.28 | 128 |
| 100 kΩ | 40.6 | 4.06 | 0.406 | 40.6 |
| 1 MΩ | 128 | 12.8 | 0.128 | 12.8 |
| 10 MΩ | 406 | 40.6 | 0.0406 | 4.06 |
| 100 MΩ | 1280 | 128 | 0.0128 | 1.28 |
Амплитуда теплового шума в общем случае величина хотя и непредсказуемая, но зато соответствующая распределению Гаусса ( рис. 8.2 ), где \( p( V)dV\) – вероятность того, что мгновенное значение лежит между \( V \) и ( \( V+dV\) ) и \(v_n( rms ) \) - среднеквадратическое напряжение шума, заданное ранее _7 .
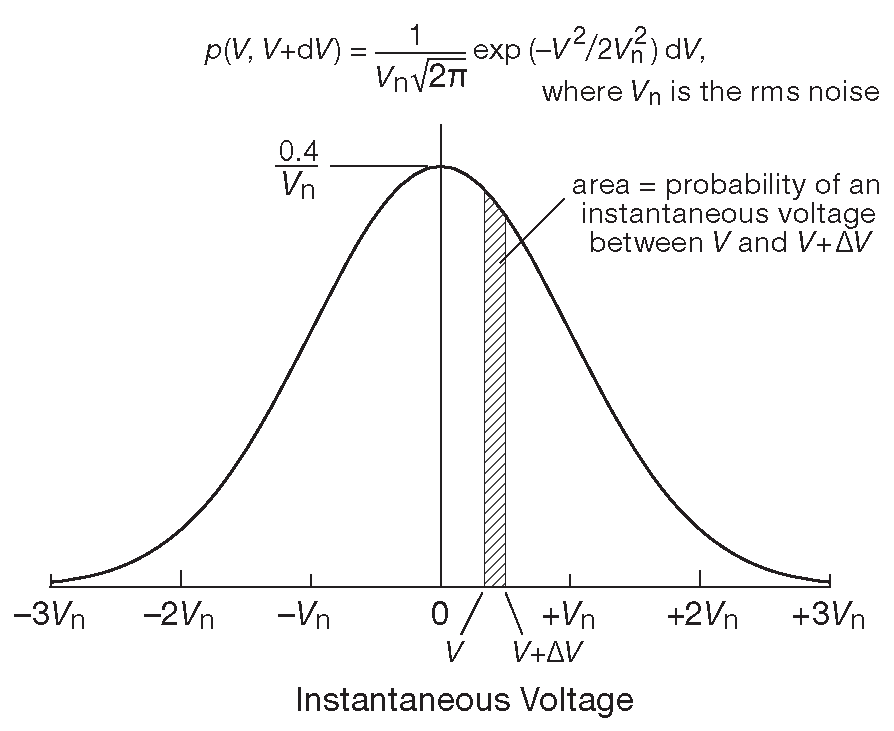
Рис.8.2 Тепловой ток имеет гауссово распределение амплитуд. Коэффициент нормировки для площади фигуры под графиком 0.4\(/v_n\) ( 0.4 на самом деле равно 1/\(\sqrt{2π}\) или 0.3989 )
Смысл теплового шума в том, что он задаёт нижнюю границу шумов любого детектора, источника сигнала или усилителя, обладающего сопротивлением. Резистивная часть полного сопротивления источника создаёт тепловой шум так же, как входное сопротивление любого усилителя или сопротивление его нагрузки. Скоро будет показано, как это происходит.
Интересно отметить, что физические аналоги сопротивления ( какой-либо механизм рассеяния энергии в физической системе, например, вязкое трение, действующее на небольшие частицы в жидкости ) связаны с их колебаниями в конкретном физическом объёме ( в нашем случае, движение частиц, называемое «броуновским движением» ). Тепловой шум - один из видов этого диссипативного процесса.
Тепловой шум не следует путать с дополнительным шумовым напряжением в резисторе, возникающим при слабых колебаниях сопротивления под действием внешнего тока. Этот «дополнительный» шум имеет спектр 1/\( f \) ( приблизительно ) и очень сильно зависит от конструкции резистора. Данное явление будет рассматриваться позднее.
8.1.2 Дробовый шум
Электрический ток - упорядоченное движение отдельных заряженных частиц, т.е. дискретных зарядов, а вовсе не непрерывное плавное течение. Конечность квантов заряда ведёт к статистическим вариациям тока. Элементарные заряды действуют независимо друг от друга, соответственно, изменение интенсивности шумового ток подчиняется закону \[ i_n=\sqrt{2qI_{dc}} \qquad \qquad \mathrm {A/\sqrt{Hz}} , \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.6] \]
где \(q\) - заряд электрона ( \(1.6×10^{-19}\) кулона ). Этот шум, как и тепловой шум резистора, является белым и гауссовым, поэтому его амплитуда, измеренная в полосе частот BW , равна \[ i_{noise}(rms)=i_{nR}(rms) = i_n\sqrt{BW}=\sqrt{2qI_{dc}BW} \qquad\mathrm{A/\sqrt{Hz}}. \qquad [8.7] \]
==476
Например, «установившийся» ток 1A в полосе 10 kHz имеет на самом деле среднеквадратическое значение флуктуаций 57 nA , т.е. переменная составляющая имеет величину 0.000'006% . Относительные значения отклонений повышаются со снижением абсолютной величины тока: «установившийся» ток 1 μA в той же полосе 10 kHz имеет среднеквадратическое значение шума 0.006% или -85 dB . Для 1 pA и 10 kHz флуктуации составят уже 57 fA или 5.7% ! Дробовый шум напоминает стук дождя по железной крыше.
Ниже приводится небольшая таблица плотности шума в полосе 10 kHz для токов, меняющихся в диапазоне 12 декад.
| \(I_{dc}\) | \(i_n\) | \(i_n\sqrt{BW}\) | \({(i_n\sqrt{BW} )}/{I_{dc}}\) |
| 1 fA | 18 aA/\(\sqrt{Hz}\) | 1.8 fA | +5 dB |
|---|---|---|---|
| 1 pA | 0.57 fA/\(\sqrt{Hz}\) | 57 fA | -25 dB |
| 1 nA | 18 fA/\(\sqrt{Hz}\) | 1.8 pA | -55 dB |
| 1 μA | 0.57 pA/\(\sqrt{Hz}\) | 57 pA | -85 dB |
| 1 mA | 18 pA/\(\sqrt{Hz}\) | 1.8 nA | -115 dB |
Важное замечание: приведённая выше формула дробового шума предполагает, что заряженные частицы создают ток, действуя независимо. Это и в самом деле так для зарядов, преодолевающих энергетический барьер, например, в случае тока, текущего через диод, где заряды диффундируют через p-n переход, а вот для тока в металлическом проводнике данное утверждение не верно, т.к. существует зависимость между носителями заряда, действующая на большом расстоянии. Поэтому ток в чисто резистивной схеме будет содержать гораздо меньше шума, чем предсказывает формула. Другим важным исключением для формулы является стандартный транзисторный источник тока ( рис. 2.32 ), который будет рассматриваться в §8.3.5 .
Упражнение 8.1
В малошумящем усилителе в качестве коллекторной нагрузки используется резистор. Ток коллектора \(I_C\) содержит дробовый шум. Покажите, что в шумовом напряжении на выходе дробовый шум будет выше теплового шума резистора всё время, пока падение напряжения покоя на резисторе больше \( 2kT/q\) , что составляет 50 mV при комнатной температуре.
8.1.3 Шум вида 1/f
Дробовый и тепловой шум относятся к неустранимым видам шума, своим появлением обязанным фундаментальным физическим законам. Самые дорогие и высокотехнологичные резисторы будут иметь в точности ту же величину теплового шума, что и самые дешёвые угольные того же номинала. В реальных компонентах кроме того присутствуют различные источники дополнительного шума. В настоящих резисторах присутствуют флуктуации сопротивления, создающие дополнительное ( к уже имеющемуся тепловому ) шумовое напряжение, которое пропорционально постоянной составляющей протекающего через них тока. Шум зависит от множества особенностей конструкции конкретного резистора, включая материал резистивного элемента и, главное, материала и способа соединения внешних выводов. Приведём величины дополнительных шумов для разных типов резисторов. Цифры даны в виде среднеквадратических значений в μV на V приложенного к резистору напряжения, померенных в полосе в одну декаду ( см. формулу [8.13] ):
| Углеродистые объёмные | 0.10—3.0 μV | |
| Углеродистые плёночные | 0.05—0.3 μV | |
| Металлоплёночные | 0.02—0.2 μV | |
| Проволочные | 0.01—0.2 μV |
Фликкер-шум имеет спектр вида 1/\( f \) ( равный мощности на декаду частоты ) и его иногда называют «розовым» шумом. Если строить зависимость амплитуды шума не от мощности, а от тока через резистор или приложенного к нему напряжения, то будет видно, что амплитуда падает пропорционально 1/\(\sqrt{f}\) , как показано на рис. 8.3 . Рис. 8.4 показывает как розовый шум выглядит по сравнению с белым и «красным» - ещё одним видом шума, имеющим спектр мощности 1/\( f^2\) . Если есть желание сделать свой собственный источник шума, то можно взглянуть на схему 8.93 , чтобы узнать как.
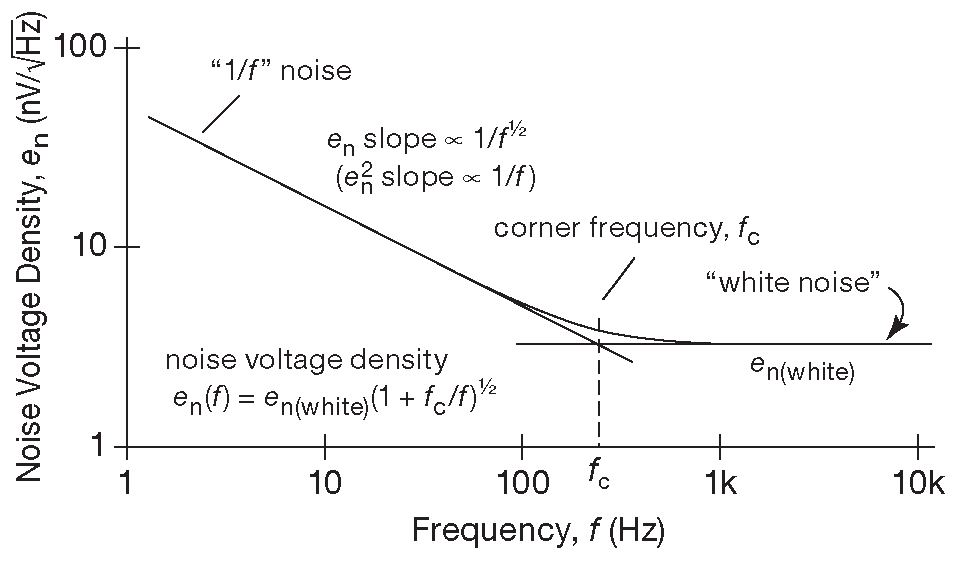
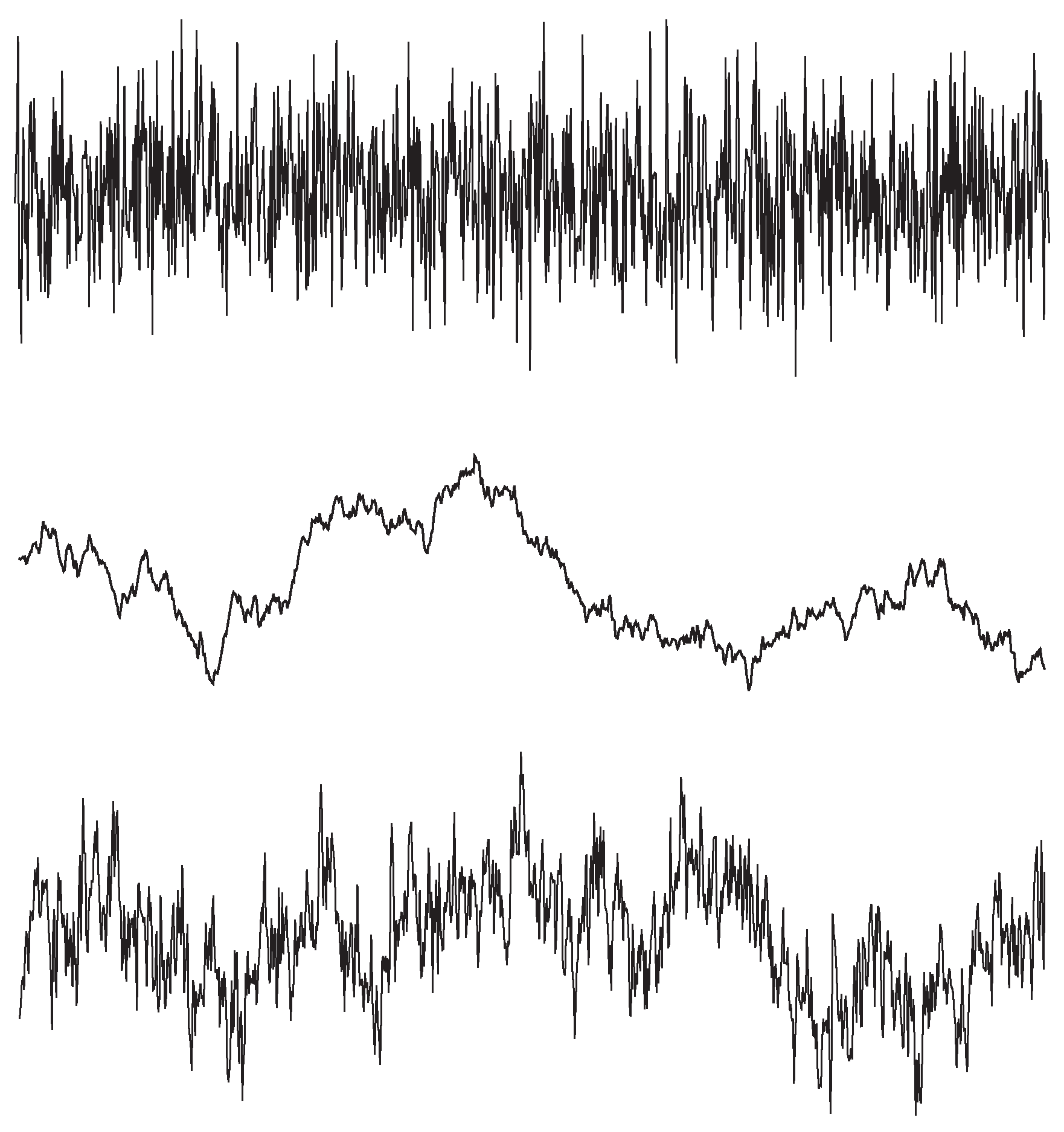
Рис.8.3 На логарифмическом графике зависимости мощности шума от частоты компонента вида 1/\( f \) падает с наклоном 1/2 , т.е. как 1/\(\sqrt{f}\) ( тогда мощность шума имеет вид 1/\( f \) )
Рис.8.4 Три вида шума: сверху - «белый» шум ( мощность постоянна во всём частотном диапазоне ); в центре - «красный» шум ( мощность пропорциональна 1/\( f^2 );\) снизу - «розовый» шум или шум вида 1/\( f \) ( мощность пропорциональна 1/\( f \) )
В литературе часто встречается обозначение \( f_c\) - «corner frequency» графика плотности шума: характеристическая частота, ниже которой шум определяется 1/\( f \) компонентой, а выше - уровнем белого шума _8 . Плотность комбинированного шума определяется уравнением \[ e_n( f)=e_{n(white )}\sqrt{1+f_c/f}, \qquad \qquad \qquad \qquad \qquad \qquad \qquad[8.8] \] по которому можно рассчитать среднеквадратический уровень суммарного шума в полосе от \( f_1\) до \( f_2 \) ( см. уравнение [8.59] на стр. 565 ).
==477
Шум вида 1/\( f \) часто сопровождает физические процессы в схемах, например, шум тока базы в транзисторах или катодный шум электронных ламп. Любопытно, что этот шум можно встретить в самых неожиданных местах: в скорости океанских печений, движении песка в песочных часах, пассажиропотоке в японских пригородных поездах и стоке Нила по наблюдениям за последние 2000 лет _9 . Если построить график громкости фрагмента классической музыки по времени, получится спектр 1/\( f \) . Общие принципы для всех этих явлений обнаружить не удаётся, хотя установить механизм в каждом конкретном случае удаётся почти всегда.
8.1.4 Импульсный шум
Гауссово ( и даже просто гладкое ) распределение амплитуды характерно не для всех источников шума. Одним из наиболее заметных исключений является импульсный шум ( иногда называемый «бистабильным», «телеграфным» и «попкорн»-шумом ). Его можно обнаружить в полупроводниковых компонентах, выпущенных преимущественно до 1970 года. Шум выглядит как случайные переходы между двумя ( обычно ) уровнями напряжения с периодом в десятки миллисекунд, а если воспроизвести его через музыкальный центр, то звук будет напоминать треск лопающейся воздушной кукурузы. Типичная форма сигнала показана на рис. 8.5 . Это выход старого 10 операционного усилителя типа 741 в неинвертирующем включении с коэффициентом усиления G=100 .
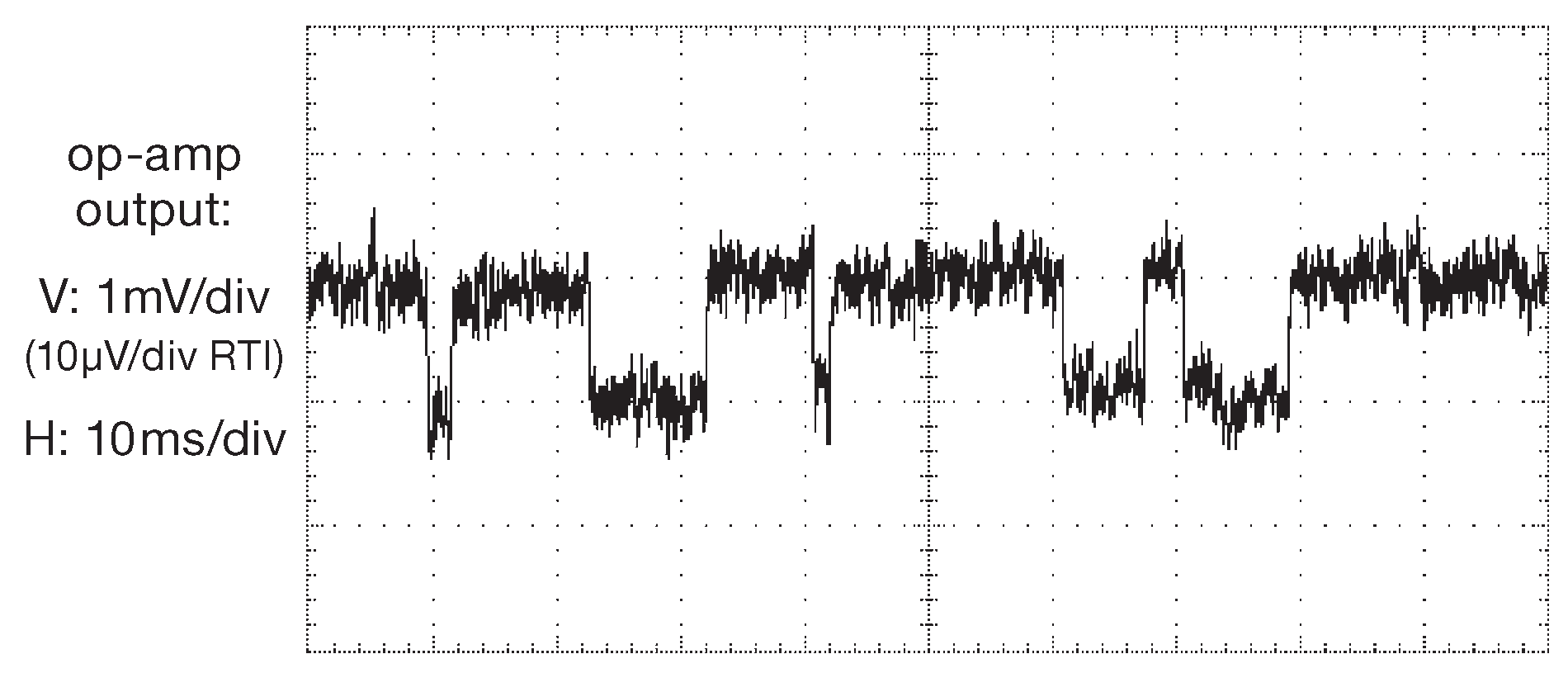
Рис.8.5 Импульсный шум ОУ 741 выпуска 1973 года в неинвертирующем включении с коэффициентом усиления G=100 и заземлённым входом. Выходной сигнал пропущен через полосовой фильтр 0.1 Hz—3 kHz со спадом 6 dB/octave
В частотной области данный вид шума демонстрирует характерный подъём в низкочастотной части спектра без каких либо заметных пиков. Его можно наблюдать на рис. 8.6 , где приводятся выходные спектры тихого и шумного образца ОУ 741 11 .
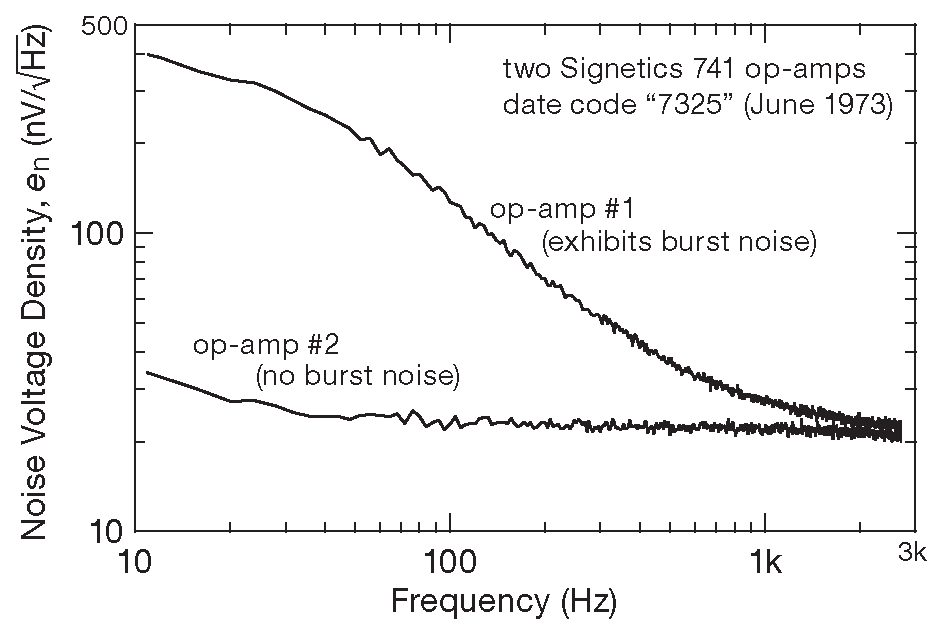
Рис.8.6 Спектр burst шума, создаваемого тем же ОУ, что и на рис. 8.5 . Для сравнения показан выходной сигнал, где шум отсутствует. Вертикальная шкала показывает среднеквадратическую плотность шума, приведённую ко входу
8.1.5 Ограниченный по полосе шум
Все электронные устройства работают в некоторой ограниченной полосе частот, поэтому, хотя приятнее говорить о плотности шума ( и использовать её в расчётах ), на самом деле заботиться приходится о среднеквадратическом напряжении шума в некоторой интересующей полосе частот ( скрывающейся за переменной BW в уравнении [8.1] ). Во многих случаях работать приходится с источниками белого шума ( т.е. с тепловым или дробовым шумом ). Если пропустить его через фильтр с чётко очерченными границами рабочей полосы ( фильтр с вертикальными срезами, напоминающими кирпичную стену ), то среднеквадратическая амплитуда в ограниченной полосе равна просто \(v_n(rms)=e_n\sqrt{BW}\). Но аналоговые фильтры с такими характеристиками непрактичны, поэтому всё, что требуется знать - это эквивалентную [* идеальную] полосу реального фильтра, например, RC цепочки. С другой стороны, для RC фильтра справедливо соотношение: \[ BW=\frac{π}{2}f_{3dB}=1.57f_{3dB}=\frac{1}{4RC}\qquad \mathrm {Hz}, \qquad \qquad \qquad \qquad [8.9] \]
==478
где \( f_{3dB}=1/( 2πRC ) \). Конечно, можно использовать фильтры и более высоких порядков, например, двухзвенный ФНЧ Баттерворта, чья полоса заграждения ( «кирпичная стенка» ) ограничена частотой BW=1.11×\(f_{3dB}\) . Соотношения для фильтров высоких порядков можно посмотреть в табл. 8.4 ( стр. 564 ). Для медленно меняющихся сигналов ( или постоянных уровней ) можно использовать простое усреднение ( пример для интегрирующего АЦП см. в §13.8.3 ) В этом случае эквивалентная полоса шума BW=1/(2T) , где T - длительность усреднённого входного сигнала. Продолжение обсуждения этого вопроса см. в §8.13.1 .
Спектр шума может быть и не белым ( например, вида 1/\( f \) или комбинация белого и низкочастотного подъёма вида 1/\( f \) ) . В таком случае уже нельзя просто умножать плотность шума на корень из рабочей полосы. Вместо этого надо интегрировать меняющуюся плотность шума по всей рабочей полосе. В случае идеального полосового фильтра с вертикальным переходом от пропускания к заграждению получаем \(v_n^2=\int e_n^2( f)df\) в промежутке между нижней и верхней частотами заграждения. В пригодных для реализации фильтрах необходимо интегрировать плотность шума, скорректированную на спектральный отклик фильтра \(H( f ) \) в полосе пропускания [* чья АЧХ может быть «не совсем» и даже «совсем не» плоской] , т.е.: \(v_n^2=\int | e_n( f)H( f)|^2df\) . Это то, что необходимо делать в случае произвольного спектра шума. Жизнь немного упрощается, если речь идёт об известном спектре, например, шуме вида 1/\( f \) , который допускает аналитическое решение. Все эти особенности собраны в табл. 8.4 ( стр. 564 ), включающей данные для белого, розового и красного спектра шума в полосе, ограниченной идеальным фильтром ( кирпичной стенкой ), однозвенным, двухзвенным и n-звенным полосовым фильтром Баттерворта ( с границами на частотах \( f_1\) и \( f_2 \) ) . Эти табличные формулы позволяют рассчитать как ФНЧ ( \( f_1=0\) ) , так и ФВЧ ( \( f_2=∞\) ) , которые являются частным случаем более общего полосового фильтра.
Более подробное обсуждение со множеством деталей см. в §8.13 .
8.1.6 Интерференция
Как уже говорилось ранее, интерференция сигнала или сторонняя наводка – суть одна из форм шума. Отсюда, его спектральные и амплитудные характеристики зависят от сигнала наводки. Например, 60 Hz наводка имеет узкий пик и относительно стабильную амплитуду, а шум от автомобильного зажигания, молний и других импульсных источников имеет широкий игольчатый спектр. Кроме того, источниками интерференции являются теле- и радиостанции ( представляющие серьёзную проблему в больших городах ), близлежащее электрооборудование, электромоторы, лифты, линии метро, ключевые источники питания и даже телеприёмники. Часто все другие источники радиочастотной интерференции затмевает сотовая связь. Даже в отсутствие разговора включённый телефон периодически сообщает базовой станции своё местоположение, создавая наводку с характерным скачущим ритмом 12 . Такую же картину создают мобильные компьютеры, использующие сотовую связь для выхода в интернет.
Несколько иначе выглядят проблемы, которые возникают из-за привнесённого в измеряемую величину стороннего сигнала. Например, оптический интерферометр чувствителен к вибрациям, а тонкие измерения в радиочастотной области (ядерно-магнитный резонанс) нуждаются в защите от внешних электромагнитных полей. Многие устройства, в т.ч. детекторы и даже кабели, реагируют на сотрясения и звук, т.е. проявляют «микрофонный эффект».
Некоторые из этих источников шума можно отсечь аккуратной экранировкой и фильтрацией. Другие вынуждают чрезвычайно строго подходить к процессу измерения: использовать массивное каменное основание ( для защиты от вибрации ), термостатированную комнату, безэховую камеру и полностью заэкранированную комнату ( «клетка Фарадея» ).
==478
3 См. §8.14 и Часть_15 второго издания ( 1989 ) этой книги. <-
4 Лью Бранскомб ( Lew Branscomb) хорошо отметил: «Природа «не знает» какой именно эксперимент собирается проводить учёный. Господь любит шум так же, как и сигнал» L.Branscomb, “Integrity in Science”, Am. Sci. 73, 421-23 ( 1985 ). <-
5 Эксперимент и формулы: J. B. Johnson, Letter to Nature, 119, 50 ( 1927 ), Phys. Rev. 32, “Thermal agitation of electricity in conductors”, 97-109, ( 1928 ), теоретическое обоснование: H. Nyquist, Phys. Rev., “Thermal agitation of electric charge in conductors”, 32, 110-113, ( 1928 ). <-
6 Авторы находят удобным помнить значения «q» и «4kT» ( которые будут встречаться постоянно ), потому что в системе СИ они имеют значения \(1.6×10^{-19}\) и \(1.6×10^{-20}\) соответственно. <-
7 См. также рис. 8.115 , на котором изображены отклонения ( в диапазоне девяти декад ) мгновенных значений амплитуды от некоторого усреднённого среднеквадратического значения. <-
8 Рассчитать частоту \( f_c\) можно с помощью уравнения [8.27] ( стр. 491 ). <-
9 Интересную подборку можно найти в работе «Фликкер шумы в астрономии и вокруг нас» W. H. Press, “Flicker noises in astronomy and elsewhere”, Comm. On Astrophys. 7, 103-119 ( 1978 ). Её можно найти по адресу: http://www.nr.com/whp/Flicker_Noise_197 8.pdf. <-
10 Производители электронных компонентов активно работали над преодолением этой проблемы ( предполагается, что он вызывается отдельными носителями заряда, застревающими в дефектах кристаллической решётки ) и на данный момент этот вид шума в основном остался в прошлом. Чтобы получить сигнал для рис. 8.5 были перепробованы десять образцов шести разных производителей, а найдена была только одно микросхема. Второй образец той же компании и с той же датой производства подобного дефекта не имел ( см. пару спектров на рис. 8.6 ). <-
11 Возможно, что подобный же механизм ответственен за аналогичное плато в шумовых спектрах некоторых полевых транзисторов: см. пример с LSK389 на рис. 8.47 . <-
12 Его можно услышать по адресу www.covingtoninnovations.com/michael/blog/0506/050622-cellnoise.mp3. <-

