8.2 Отношение сигнал-шум и коэффициент шума
==478
Прежде чем разбираться в деталях шумов усилителей и разработки малошумящей аппаратуры, необходимо дать определения некоторых терминов, часто используемых при описании характеристик усилителей. Они предполагают измерение отношения шумовых напряжений, измеренных в определённой точке схемы. Общепринятой практикой является приведение шумовых напряжений ко входу усилителя ( хотя сами измерения обычно проводятся на выходе ), т.е. то напряжение шума, которое вызывает появление на выходе наблюдаемого сигнала. Это имеет смысл, если считать, что добавляемый усилителем шум не зависит от самого усиления. Подход достаточно реалистичный, потому что обычно бОльшую часть шума вносит входной каскад. Таким образом, во всех случаях, когда не указано иное, под шумовым напряжением будем понимать шум, отнесённый ко входу ( RTI ).
==479
8.2.1 Плотность мощности шума и рабочая полоса частот
В предыдущих примерах теплового и дробового шума измеренное напряжение шума зависело как от полосы измерения BW ( т.е. на уровень шума влияет длительность процесса измерения ), так и от параметров ( \(R\) и \(I\) ) самого шума. Поэтому принято говорить о «плотности» среднеквадратичного напряжения шума \(e_n:\) \[ v_n(rms)=e_n\sqrt{BW} = \sqrt{4kTR}\sqrt{BW} \qquad \mathrm {V(rms)} , \qquad [8.10] \] где \(v_n\) - среднеквадратическое напряжение шума, измеренное на полосе BW . Источники белого шума имеют \(e_n\) , которое не зависит от частоты, а для розового шума \(e_n\) падает с наклоном 3 dB/octave . Часто можно увидеть и \(e_n^2\) – квадрат плотности. Так как \(e_n\) всегда подразумевает среднеквадратическое напряжение, а \(e_n^2\) означает квадрат напряжения, то, чтобы получить \(e_n^2\) , надо просто возвести в квадрат \(e_n\) . Выглядит слишком просто ( и в самом деле так ), но для уверенности, что никто ничего не перепутает, приведём пример для теплового шума резистора \(R:\) \[\begin{align*} e_{nR}(rms) &= \sqrt{4kTR} &\space &\mathrm {V/ \sqrt{Hz}} \\ e_{nR}^2 &= 4kTR &\space &\mathrm {V^2/Hz} \\ v_n(rms) &= v_{nR}\sqrt{BW} &\space = \sqrt{4kTR×BW} \space \space \space &\mathrm {V} \\ v_n^2 &= v_{nR}^{2}BW &\space = 4kTR×BW . \space \quad &\mathrm {V^2} \end{align*} \]
Отметим, что BW и «квадратный корень из BW» сохраняются.
В технических данных можно видеть графики \(e_n\) и \(e_n^2\) в единицах «nV/\(\sqrt{Hz}\)» или «V2/Hz». Шумовой ток - \(i_n\) - работает в формулах так же и считается аналогично.
При сложении двух независимых сигналов ( от двух источников шума или шум и полезный сигнал) складывается их мощность, т.е. квадраты амплитуд: \[v=\sqrt{(v_s^2+v_n^2 )} \quad,\]
где \(v\) - среднеквадратическое значение, получаемое при сложении среднеквадратического значения амплитуды \(v_s\) сигнала и среднеквадратического значения амплитуды \(v_n\) шума. Сами амплитуды 13 не складываются.
8.2.2 Отношение сигнал-шум
Отношение сигнал-шум ( SNR ) задаётся просто: \[ \mathrm{SNR} = 10\lg(v_s^2/v_n^2 ) = 20\lg(v_s/v_n ) \qquad \mathrm {dB} ,\qquad [8.11] \] где напряжения - среднеквадратические значения, плюс задаётся полоса и её центральная частота. Другими словами, это отношение в децибелах среднеквадратического значения сигнала к среднеквадратическому значению шума 14 . Сам «сигнал» при этом может быть синусоидальным, а может быть и модулированной информационным пакетом, ли даже шумоподобной посылкой. Если сигнал имеет узкий спектр, то важно указывать его рабочую полосу, потому что SNR снижается по мере увеличения ширины полосы, т.к. усилитель продолжает добавлять шум, а мощность сигнала остаётся постоянной.
8.2.3 Коэффициент шума
Любой источник сигнала и любая измерительная схема создаёт шум, т.к. всегда есть тепловой шум их сопротивления ( активной части полного импеданса ), Кроме того, могут возникать шумы и другой природы. Коэффициент шума усилителя ( NF ) - это отношение в децибелах выходного сигнала реального усилителя и выходного сигнала идеального бесшумного усилителя с таким же усилением и эквивалентным сопротивлением \(R_S\) на входе. Другими словами, тепловой шум резистора \(R_S\) является «входным сигналом»: \[ \begin{align*} \mathrm{NF} &= 10\lg \left( \frac{4kTR_S+v_n^2}{4kTR_S} \right ) & [8.12] \\ &= 10\lg \left(1+ \frac{v_n^2}{4kTR_S} \right ) \qquad \mathrm {dB} , & [8.13] \end{align*} \] где \(v_n^2\) - квадрат амплитуды на герц усреднённого шума, вносимого усилителем, имеющим на входе холодное ( бесшумное ) сопротивление \(R_S\) . Это ограничение очень важно, потому что, как будет ясно из дальнейшего, вносимый усилителем шум сильно зависит от сопротивления источника ( рис. 8.7 ).
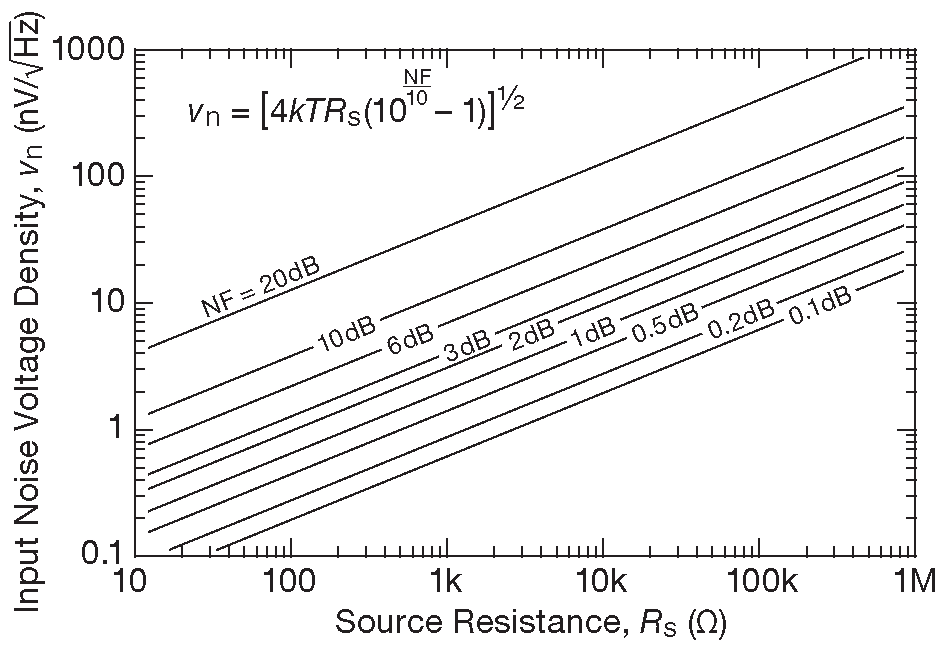
Рис.8.7 Эффективная плотность входного напряжения шума в зависимости от коэффициента шума и сопротивления источника
Коэффициент шума удобен для оценки качества, когда есть источник сигнала с известным импедансом и нужно сравнить два усилителя ( или транзистора, для которых часто тоже указывают этот параметр ). Коэффициент шума меняется с частотой и сопротивлением источника и часто даётся в виде набора контурных кривых равных значений NF для какой-либо частоты или некоторого значения \(R_S\) ( примеры можно увидеть на рис. 8.22 и 8.27 ). Либо в виде набора графиков изменения NF по частоте или по \(R_S\) отдельной кривой каждого конкретного тока коллектора.
Примечание: все нижеследующие формулы для коэффициента шума предполагают, что входной импеданс усилителя много больше, чем импеданс источника, т.е. \(Z_{in}≫ R_S\) . Но есть специальный случай радиочастотных усилителей, где \(R_S=Z_{in}\) = 50 Ω с соответствующим образом заданным коэффициентом шума. Это случай согласованных импедансов, и для него из соотношений [8.12] и [8.13] надо убрать множитель «4».
==480
Грубая ошибка: не следует пытаться обойти проблему простым добавлением резистора последовательно с источником сигнала, чтобы попасть в область с низким значением NF на графике. В итоге просто сильно возрастёт шум источника, и усилитель будет выглядеть лучше на его фоне ! Здесь NF только сбивает с толку. Чтобы дополнительно всё запутать, значение NF ( например, NF=2 dB ) транзистора всегда будет указано для оптимального сочетания \(R_S\) и \(I_C\) и не скажет о параметрах ничего, кроме того, что по мнению производителя коэффициент шума - характеристика, которой не грех и похвастаться.
В общем случае, отношение сигнал-шум для заданного напряжения сигнала и импеданса источника - последнее, на чём хотелось бы проколоться при расчёте параметров усилителя, поэтому будет полезнее придерживаться следующей формулы для перехода от NF к SNR : \[ \mathrm{SNR} = 10\lg \left( \frac{v_s^2}{4kTR_S} \right ) - \mathrm{NF}( R_S ) \qquad \mathrm {dB} , \qquad [8.14] \]
где \(v_s\) - среднеквадратическое значение амплитуды сигнала, \(R_S\) – импеданс источника, NF - коэффициент шума усилителя для источника с сопротивлением \(R_S\) . Примеры расчёта можно посмотреть в §8.3.1 и §8.5.6 .
8.2.4 Температура шума
Иногда вместо «коэффициента» шума среди данных для расчёта параметров усилителя можно встретить «температуру» шума . Оба варианта расчёта эквивалентны и дают один и тот же результат - дополнительный шум, вносимый усилителем в сигнал источника с импедансом \(R_S\) .
Что такое температура шума можно понять из рис. 8.8 . Для начала надо представить реальный (шумящий ) усилитель, подключённый к идеальному ( не шумящему ) источнику сигнала с импедансом \(R_S\) ( рис. 8.8 A ). В качестве такого источника можно взять резистор с сопротивлением \(R_S\) , охлаждённый до абсолютного нуля. На выходе схемы будет присутствовать какой-то шум, целиком определяемый шумом усилителя. Теперь возьмём вторую схему ( рис. 8.8B ) из бесшумного усилителя и сопротивления \(R_S\) , нагретого до некоей температуры \( T_n\) , при которой напряжение шума схемы 8.8B равно напряжению шума схемы 8.8 A . Полученная температура \( T_n\) называется температурой шума усилителя для источника сигнала с импедансом \(R_S\) .
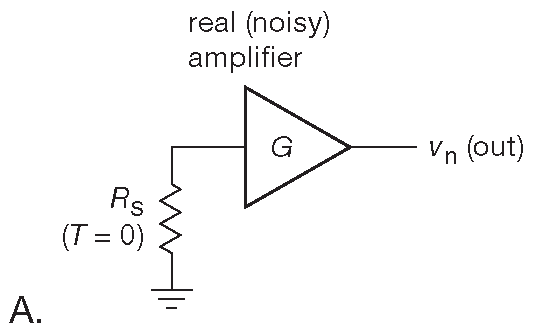
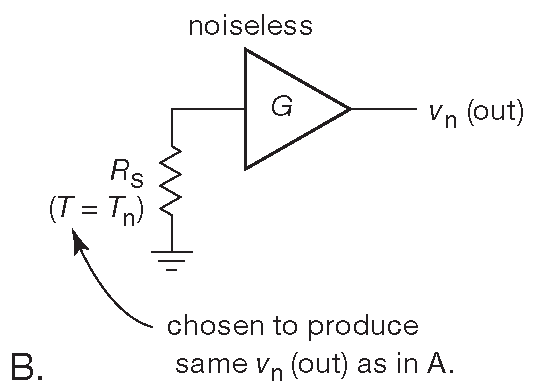
Рис.8.8 Температура шума
Как отмечалось ранее, форма шума и его температура - просто две разных формы подачи одной и той же информации. Можно показать, что они связаны следующими пропорциями: \[ T_n=T \left( 10^{\mathrm{NF( dB )}/10} -1 \right ) \qquad \mathrm{K} , \qquad [8.15] \\ \mathrm{NF( dB )}= 10\lg \left( \frac{T_n}{T}+1 \right ), \qquad \qquad [8.16] \] где T - рабочая температура, которую обычно принимают за 293 K .
В общем случае хороший малошумящий усилитель имеет шумовую температуру гораздо ниже, чем комнатная ( или, что то же самое, коэффициент шума сильно меньше 3 dB ). Ниже будет показано, как следует подступать к измерению коэффициента ( или температуры ) шума усилителя, но сначала надо разобраться с шумом транзистора и принципами создания малошумящих схем. Постараемся прояснить этот запутанный вопрос.
==480
13 Амплитуда - удобная и привычная величина для паспортных данных, справочников и т.д. Например, мы привыкли считать усилитель с шумом 3 nV/\(\sqrt{Hz}\) тихим, а сказать то же про усилитель с шумом \(0.9×10^{-17} V^2/Hz\) труднее. <-
14 Подобное соотношение для квадратов амплитуд соответствует отношение их мощностей, которое является основным определением для децибел. Но форма «20 lg» используется столь же широко, даже когда речь идёт не о реальной мощности, например, о ненагруженной схеме. Или ещё менее очевидный вариант, когда результат не совпадает с измеренным отношением мощностей как при аналитическом описании амплитуд напряжений в сигнальном трансформаторе. <-

