8.3 Шум биполярного транзистора

==481

Шум, создаваемый усилителем, легко можно описать с помощью простой модели, которая обеспечивает достаточную для большинства применений точность. В модели транзистора на рис. 8.9 $e_n$ и $i_n$ представляют внутренние источники шума транзистора: $e_n$ включается последовательно с источником сигнала, а $i_n$ - параллельно ему. Сам транзистор ( или в общем случае усилитель ) считается бесшумным компонентом, который просто усиливает шумовые напряжения на входе: своё собственное $e_n$ и падения напряжения на импедансе источника $R_S$ , вызванное протеканием через него тока $i_n$ . Таким образом, на входе усилителя действует суммарное напряжение шума $e_a$ , равное: \[ e_a(rms) = \sqrt{e_n^2+( R_Si_n )^2} \qquad \mathrm {V / \sqrt{Hz}} \qquad [8.17] \]

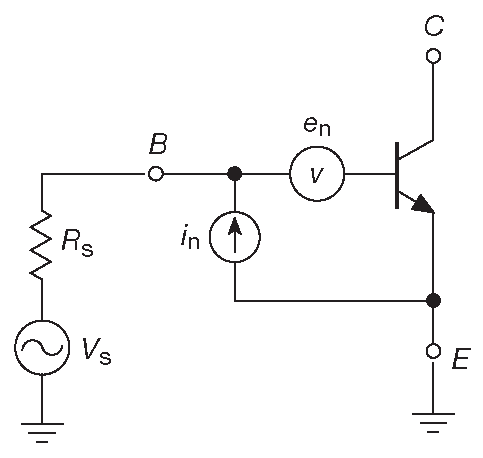
Рис.8.9 Шумовая модель транзистора

Оба слагаемых ¹⁵ являются просто квадратами напряжений, а так как это независимые слагаемые, то при вычислении действующего значения шума на входе усилителя квадраты их амплитуд просто складываются. Для низкоомных источников сигнала основной вклад вносит $e_n$ , а для высокоомных $i_n$ .

Чтобы понять, как выглядят реальные цифры, можно посмотреть на рис. 8.10 , где даны графики зависимости $e_n$ и $i_n$ от $I_C$ и $ f $ для великолепного ( но, к сожалению, снятого с производства ) ¹⁶ малошумящего npn 2SD786. Сейчас самое время углубиться в детали, которые показывают, как вести разработку, ориентируясь на минимум шума. Остаётся добавить, что шумовое напряжение и ток биполярных транзисторов лежит в диапазоне нановольт и пикоампер на корень из герц ( т.е. nV/$\sqrt{Hz}$ и pA/$\sqrt{Hz}$ ), а для МОП транзисторов шумовой ток ниже и попадает в диапазон fA/$\sqrt{Hz}$ .

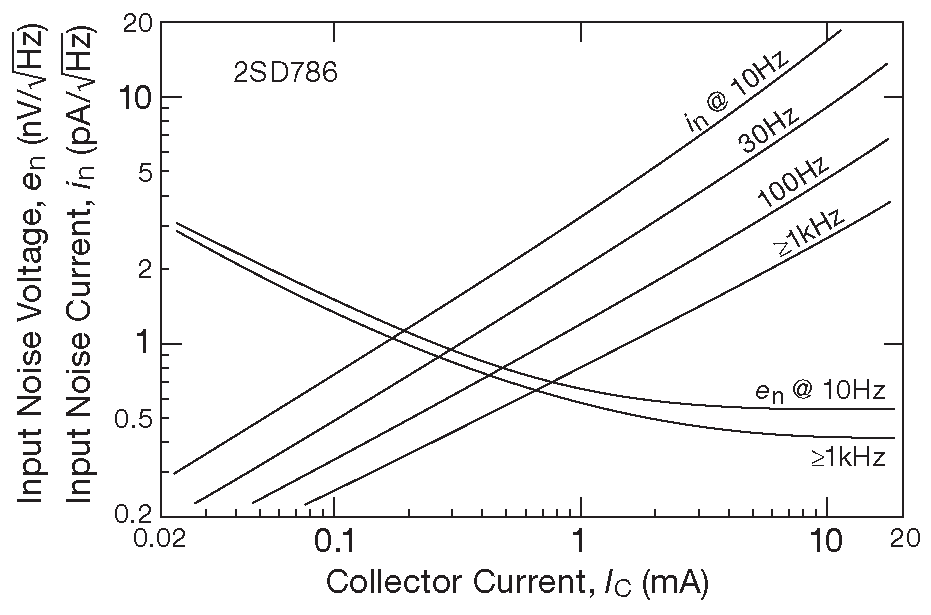
Рис.8.10 Зависимость эквивалентного среднеквадратического напряжения шума ( $e_n$ ) и шумового тока ( $i_n$ ) от тока коллектора для npn транзистора 2SD786, взятая из справочных данных

8.3.1 Напряжение шума e_n

Источник шумового напряжения , включённый последовательно с базой биполярного транзистора, порождается дробовым шумом тока коллектора, за счёт падения напряжения на внутреннем сопротивлении эмиттера $ r_e$ ¹⁷, тепловым шумом в сопротивлении базы $ r_{bb'}$ и ( как будет видно из дальнейшего ) дробовым шумом тока базы, текущим через то же сопротивление. Отбрасывая на время базовую составляющую ( которая в большинстве случаев мало влияет на напряжение шума биполярных транзисторов ), получим выражение для плотности входного напряжения шума \[ \begin{align*} e_n^2 &= 2qI_Cr_e^2+4kTr_{bb'} &\space[8.18] \\ &= 4kT \left( \frac{V_{T}}{2I_C}+r_{bb'} \right ) &\space[8.19] \\ &= 4kT \left(\frac{r_e}{2}+r_{bb'} \right ). \qquad \qquad \mathrm {V^2/Hz} \qquad &\space[8.20] \end{align*} \]

Эквивалентное преобразование $ r_e=V_{T}/I_C=kT/(qI_C$ ) позволяет избавиться от $ r_e$ в уравнении [8.19] и от $I_C$ в [8.20] .

==482

Третья форма уравнения ( [8.20] ) достаточно удобна, потому что позволяет рассматривать напряжение шума как результат сочетания теплового шума двух отдельных резисторов. Чтобы получить представление о порядке величин, полезно вспомнить, что сопротивление базы $ r_{bb'}$ типового биполярного транзистора ( см. табл. 8.1a на стр. 501 ) находится в диапазоне от нескольких ом до нескольких сотен ом. Отсюда, вклад второго слагаемого в итоговое напряжение шума составляет величину порядка 0.2 nV/$\sqrt{Hz}\space $ и 2 nV/$\sqrt{Hz}$ ( удобно запомнить, что шумовое напряжение резистора 100 Ω составляет $e_n $=1.28 nV/$\sqrt{Hz}$ , а масштабируется эта величина как $\sqrt{R}$ - корень из сопротивления [* правильно: «масштабируется как корень из отношения сопротивлений», см. пояснение в §8.13.6 ] ).

Что касается первого слагаемого уравнения [8.20] , то оно говорит, что дробовый шум коллектора через $ r_e$ создаёт такое же напряжение, как и тепловой шум воображаемого резистора с номиналом $R = r_e$/2 . Например, при токе 100 μA ( т.е. $ r_e $=250 Ω ) указанная величина равна $e_n = \sqrt{4kT·125 Ω}\space $ или 1.4 nV/$\sqrt{Hz}$ . Это полезно помнить выбирая, к примеру, номинал резистора, который не портил бы шумовых параметров усилителя. Чтобы не оставить неправильного впечатления, спешим вновь подчеркнуть, что внутреннее сопротивление эмиттера $ r_e$ имеет нерезистивную природу и теплового шума не имеет. Шумовое напряжение, о котором идёт речь, появляется исключительно из падения напряжения, создаваемого дробовым шумом коллекторного тока, текущего через бесшумный резистор $ r_e$ ¹⁸ .

Оба слагаемых шума из уравнений [8.18] и [8.20] имеют плоский ( белый ) спектр с гауссовым распределением мгновенных значений амплитуд. Сопротивление $ r_e$ падает обратно пропорционально току коллектора, соответственно, шумовое напряжение $e_n$ падает пропорционально 1/$\sqrt{I_C}$ , достигая в итоге минимума, который определяется величиной $ r_{bb'}$ ( рис. 8.11 ). Исходя из изложенного, обычно лучше работать при относительно высоких токах коллектора, если требуется минимизировать напряжение шума. Цена вопроса - увеличенный ток базы и повышенный нагрев. Возвращаясь к замечательному 2SD786, на частотах выше 1 kHz его напряжение шума $e_n $=1.5 nV/$\sqrt{Hz}$ при $I_C $=100 μA и 0.6 nV/$\sqrt{Hz}$ при $I_C $=1 mA ( рис. 8.10 ). Указанный транзистор использует специальную форму электродов, чтобы получить очень низкое значение $ r_{bb'}$=4 Ω , которое необходимо для достижения самого низкого из возможных значений $e_n$ .

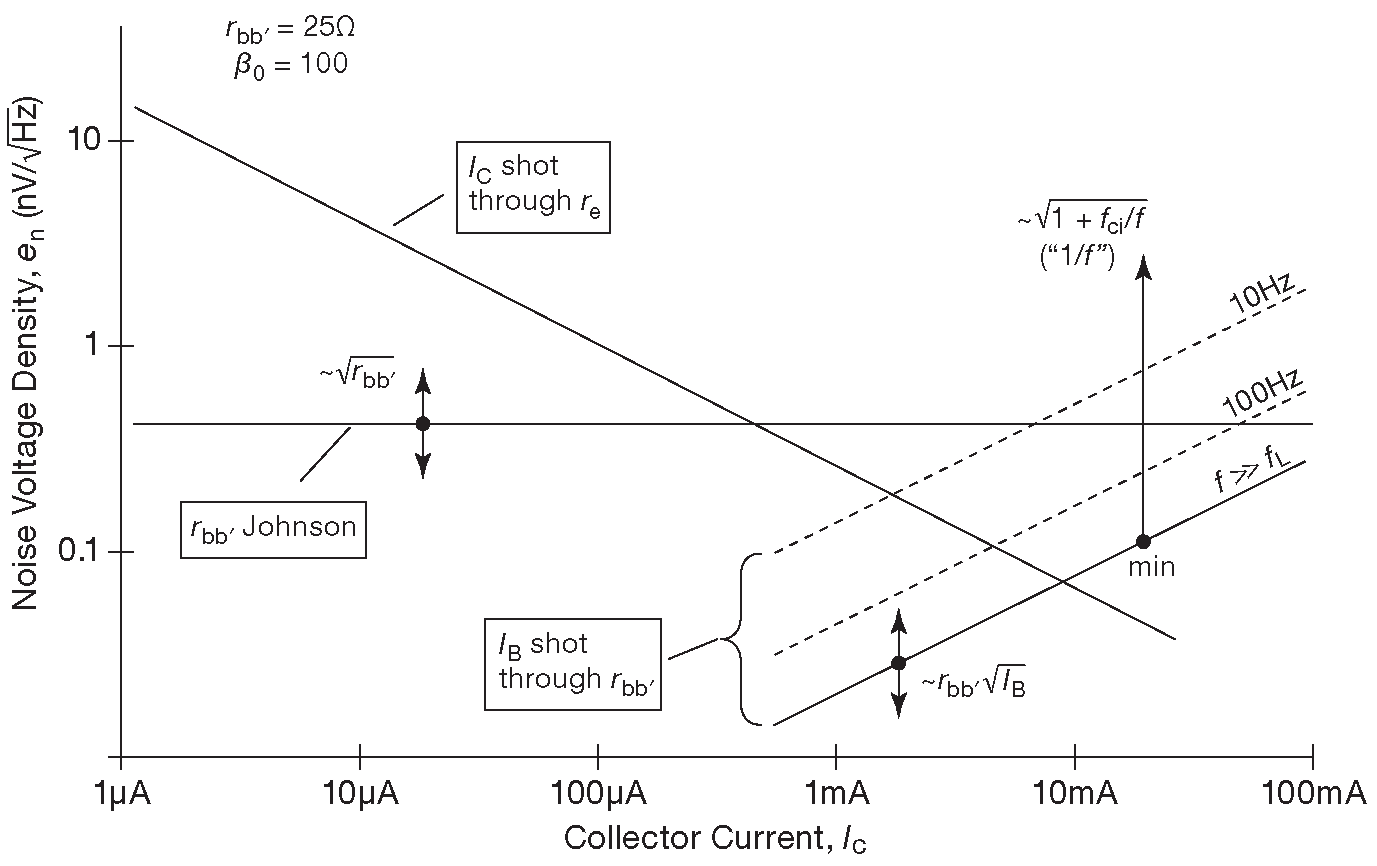
Рис.8.11 Входное напряжение шума $e_n$ биполярного транзистора. При малых токах преобладает дробовый шум $I_C$ через $ r_e$ , в остальных случаях основной вклад вносит тепловой шум $ r_{bb'}$ . Но для случая низких частот и больших токов дробовый шум тока базы через $ r_{bb'}$ опять вызывает подъём $e_n$ . Графики предполагают типовые значения точки перегиба фликкер-шума ( $ f_{ci}$ ≈ 1 kHz ) и сопротивления базы ( $ r_{bb'}$ ≈ 25 Ω ). Двунаправленные стрелки указывают разброс, вызванный изменением $ r_{bb'}$ , а стрелка, направленная вверх от точки «min», отражает рост по закону 1/$ f $ с уменьшением частоты

Конечно, если приходится работать при низких токах коллектора ( где доминируют эффекты $ r_e$ ), никаких выгод от снижения $ r_{bb'}$ нет. Для иллюстрации этого тезиса приводится рис. 8.12 , показывающий расчётную и измененную зависимость $e_n$ от тока коллектора для шести малошумящих npn транзисторов, при использовании упрощённой модели с одним параметром $ r_{bb'}$ . Выбор модели с низким $ r_{bb'}$ начинает сказываться только на больших токах, на которых придётся работать, чтобы достичь значений $e_n$ , меньших 1 nV/$\sqrt{Hz}$ ¹⁹ . Данное утверждение будет проиллюстрировано в §8.5.9 на примере входного каскада с $e_n$ < 0.1 nV/$\sqrt{Hz}$ .

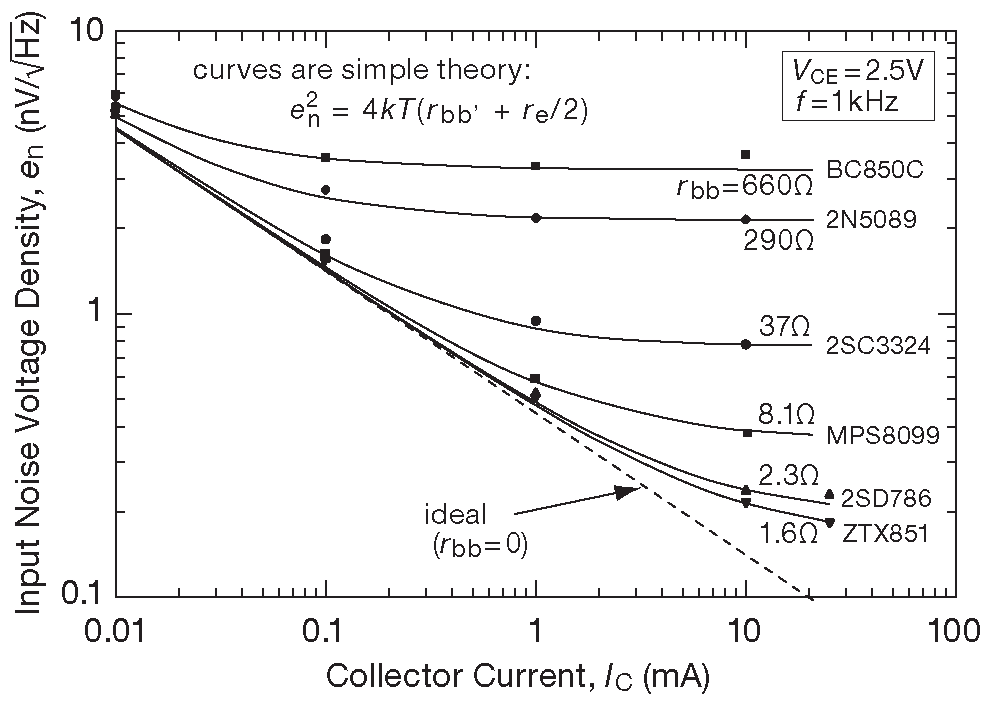
Рис.8.12 Упрощённая модель шумового напряжения транзистора ( дробовый шум тока через $ r_e$ и тепловой шум сопротивления базы изображены непрерывными линиями ) даёт неплохое приближение к измеренным значениям шума шести типов транзисторов ( четыре точки получены при разных токах ). Штриховая линия обозначает теоретический минимум при заданном токе $I_C$ в соответствии с уравнением [8.18] . Измеренное значение шума на 10%...20% выше упрощённой модели при токах ниже 100 μA . Спектры шума для этих же шести типов транзисторов при токе $I_C$=10 mA приведены на рис. 8.17

==483

Плотность напряжения шума $e_n$ на 1 kHz , показанная на рис. 8.12 , - это, конечно, ещё не вся история. Если важен шум на низких частотах, придётся побеспокоиться о его частотно-зависимых компонентах, обычно имеющих подъём вида 1/$ f $ ниже точки излома характеристики $ f_c$ . Для биполярных транзисторов этот шум обуславливается ещё одним слагаемым, которое до настоящего момента не учитывалось, - падением напряжения, возникающим при прохождении собственного шумового тока базы $i_n$ через внутреннее сопротивление базы $e_n = i_n · r_{bb'}$ . Это слагаемое становится заметным только на низких частотах и относительно больших токах коллектора, но оно достаточно важно по другой причине: шумовой ток базы протекает через импеданс источника входного сигнала, создавая дополнительное напряжение шума $v_n = i_n R_S$ . Рассмотрим методы работы с шумовым током, после чего вновь вернёмся к напряжению шума $e_n$ , но уже с учётом нового эффекта.

8.3.2 Токовый шум i_n

Входной шумовой ток транзистора создаёт дополнительный шумовой потенциал на внутреннем сопротивлении источника сигнала. Основным источником этого шума является дробовая составляющая установившегося тока базы: \[ i_n=\sqrt{2qI_B}=\sqrt{2qI_C/β_0} \qquad \mathrm{A/\sqrt{Hz}} \qquad [8.21] \] которая является шумом с плоским частотным спектром ( т.е. «белым» ) и гауссовым распределением. В формуле используется символ $β_0$ , чтобы подчеркнуть, что это бета на постоянном токе.

Есть ещё одна частотно-зависимая составляющая шума, которая поднимает свою ужасную голову на низких частотах. Она имеет типовую зависимость вида 1/$ f $ с перегибом характеристики на частоте $ f_{ci}$ , т.е. вносит слагаемое $ 2q·I_B·f_{ci}\space /f$ в общую цифру $(i_n)^2$ . Эта фракция с увеличением $I_C$ растёт быстрее, вызывая смещение графика 1/$ f $ вправо, с типовой зависимостью роста $ f_{ci}$ от $ (I_B )^{1/4}$ до $ (I_B )^{1/3}$ ( см. графики на рис. 8.13 и 8.14 ). Типичное значение частоты перегиба кривой шума $ f_{ci}$ составляет 50...300 Hz при токах 1...10 μA и 200 Hz...2 kHz при 1 mA .

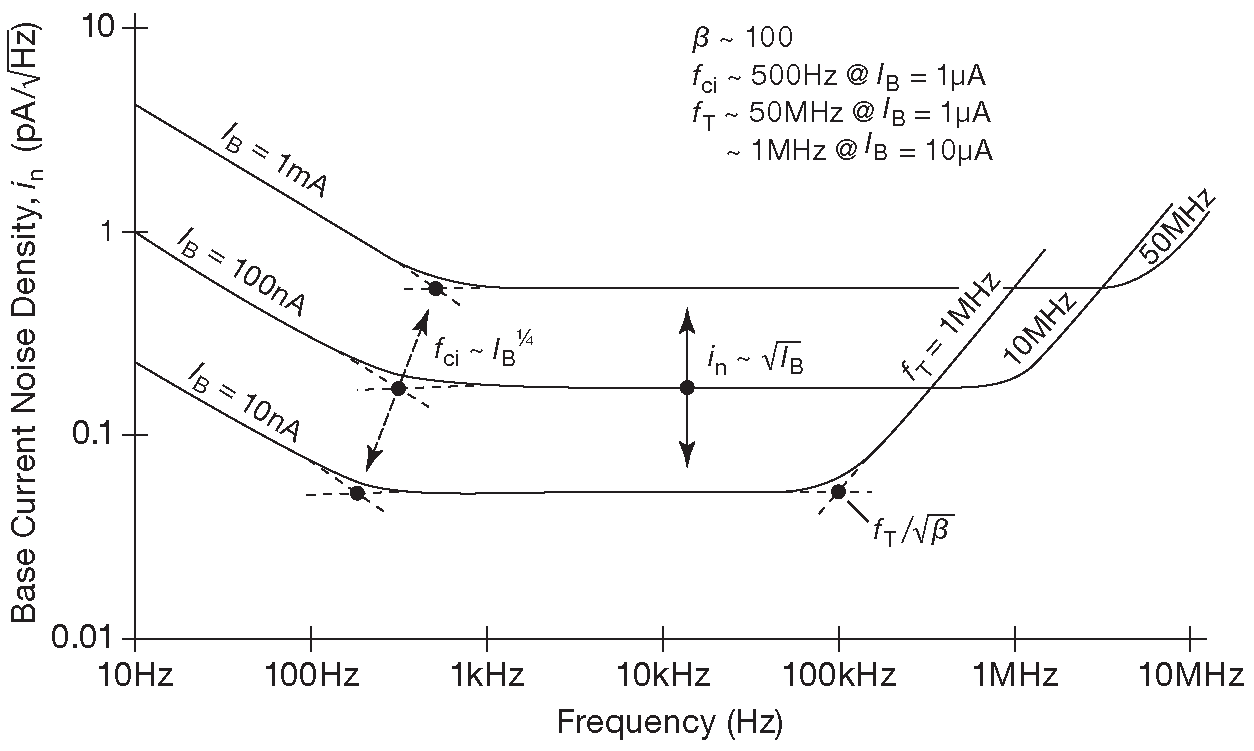
Рис.8.13 Зависимость плотность входного токового шума от частоты в биполярных транзисторах. На средних частотах это она определяется только пропорциональным $\sqrt{I_B}$ дробовым шумом тока базы. На низких частотах шум растёт как 1/$\sqrt{f}$ ( мощность шума увеличивается пропорционально 1/$ f $ ) . В любом случае точка перегиба графика $ f_{ci}$ смещается вверх с увеличением тока так, что на любой частоте ниже этой точки шумовой ток растёт быстрее, чем квадратный корень из тока базы. На высоких частотах начинает падать бета ( и становится равна единице на частоте $ f_T $ ) , вызывая неограниченный рост плотности шума ( $∝ f$ ) . Графики предполагают типовые уровни фликкер-шума ( $ f_{ci}$ ≈ 500 Hz при $I_B$= 1 μA ). Стрелки показывают изменение положения точки перегиба $ f_{ci}$ в зависимости от изменения $i_n$ тока базы

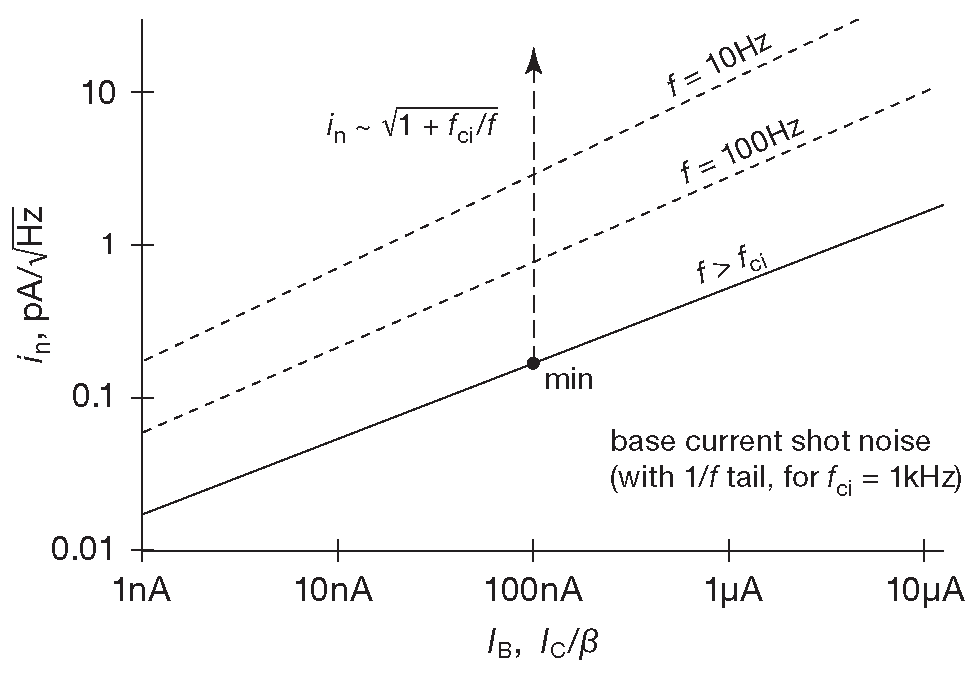
Рис.8.14 Входной шумовой ток биполярного транзистора является дробовым шумом и увеличивается как квадратный корень из тока базы для частот выше точки излома $ f_{ci}$ графика 1/$ f $ . На частотах ниже $ f_{ci}$ кривые идут круче, потому что сама $ f_{ci}$ растёт с увеличением тока ( см. рис. 8.15 )

Отметим, что упомянутый дробовый шум тока базы НЕ является шумом коллектора, уменьшенным в бета раз. Если бы это было так, его величина была бы $\sqrt{2qI_C}/β_0$ , а не как на самом деле $i_n=\sqrt{2qI_C}/\sqrt{β_0}$ в соответствии с уравнением [8.21] . В первом приближении шум тока базы не зависит от шума тока коллектора.

Данное утверждение перестаёт соответствовать действительности на высоких частотах, переходя постепенно в единый параметр токового шума: на частотах, близких к $ f_T $ ( т.е. когда коэффициент усиления приближается к единице ) уменьшившаяся бета позволяет увидеть дробовый шум тока коллектора на выводе базы.

Собирая все компоненты вместе, получаем итоговое выражение для шумового тока: \[ i_n^2=2q\frac{I_C}{β_0}\left(1+ \frac{f_{ci}}{f} \right )+ 2qI_C\left(\frac{f}{f_T} \right ) \qquad \mathrm{A^2/Hz}, \qquad [8.22] \] где последнее слагаемое учитывает изменяющуюся с частотой бету.

Возвратимся к 2SD786 ( рис. 8.10 ). Выше 1 kHz шумовой ток $i_n$ равен 0.25 pA/$\sqrt{Hz}$ при $I_C$=100 μA и 0.8 pA/$\sqrt{Hz}$ при $I_C$=1 mA . Шумовой ток увеличивается, а напряжение шума уменьшается с ростом $I_C$ . В следующем параграфе ( §8.3.3 ) объясняется, как эти параметры влияют на выбор рабочего тока схемы. На рис. 8.15 приведены графики $i_n$ в зависимости от частоты и тока для двух малошумящих транзисторов.

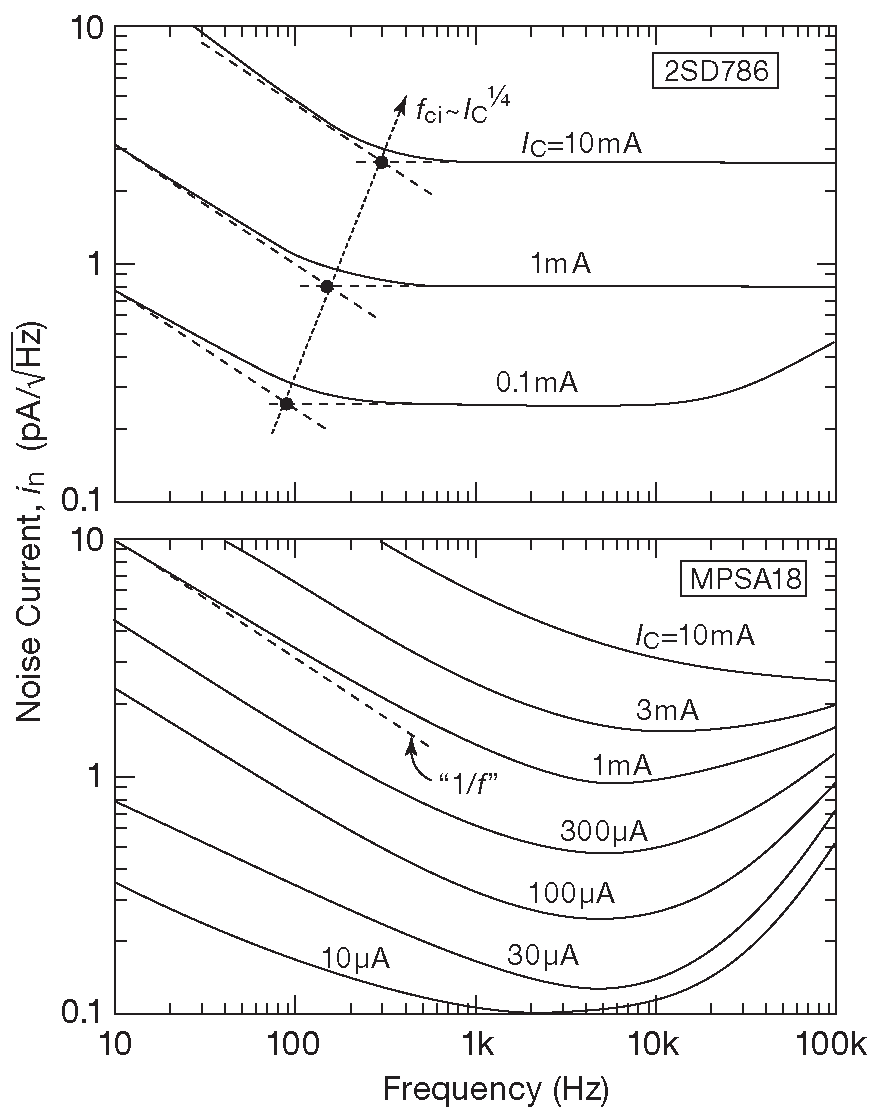
Рис.8.15 Зависимость шумового тока $i_n$ от частоты для двух типов малошумящих npn транзисторов. На низких частотах рост шумового тока чуть опережает рост тока коллектора и является причиной сдвига характеристической точки графика 1/$ f $

Воздействие шумового тока на входной импеданс

Шумовой ток, проходя через полное сопротивление источника сигнала, создаёт на этом сопротивлении напряжение шума с плотностью $v_n = i_nZ_S$ , которое складывается ( в виде суммы квадратов ) с входным напряжением шума самого транзистора ²⁰ . Обычно импеданс источника имеет резистивный характер и в этом случае появляется источник теплового шума, т.е. квадрат шумового напряжения, приведённого ко входу равен: \[ v_n^2=e_n^2+4kTR_S+(i_nR_S )^2 \qquad \mathrm {V^2/Hz}. \qquad [8.23] \]

==484

Если импеданс источника носит реактивный характер, то вклад от шумового тока ( последнее слагаемое уравнения ) будет зависеть от частоты. Типичной ситуацией, где этот факт начинает иметь значение, является включение источника сигнала через разделяющий конденсатор. Если о шуме заботиться не нужно, то конденсатор выбирается в соответствии с импедансом нагрузки ( входное сопротивление транзистора и резистор в цепи базы ), чтобы нижняя частота среза полученного ФВЧ лежала ниже нижней границы рабочей полосы. Полученная ёмкость будет невелика, если достаточно велико входное сопротивление усилителя, или нижняя рабочая частота не слишком мала. Входной шумовой ток будет создавать на разделительной ёмкости заметное напряжение шума ( естественно, изменяющееся пропорционально реактивной составляющей ёмкости $X_{c} = 1/( 2πfC) $ , т.е. пропорционально 1/$ f $ ) ²¹.

Таким образом, последовательность должна быть обратной. Сначала выбирается номинал конденсатора так, чтобы его вклад в напряжение шумов $v_n=i_nX_C$ на самой низкой рабочей частоте был небольшим ( не следует забывать, что шум тока базы часто имеет хвост вида 1/$ f $ ) . Затем рассчитываем номинал резистора в цепи базы, соответствующий нужной частоте входного фильтра. Эта неприятная проблема вылезла в самый неподходящий момент в ходе одной разработки, которую вели авторы: разделительный конденсатор создавал шумовое напряжение, менявшееся с частотой по закону 1/$ f $ ( по амплитуде, а не мощности ). Чтобы справиться с проблемой пришлось увеличивать его ёмкость в 50 раз!

8.3.3 Напряжение шума биполярного транзистора ( вторая серия )

Как утверждалось в §8.3.1 , шум входного тока транзистора $i_n$ может вносить значительный вклад в напряжение шума $e_n$ , приложенное ко входу, так как вызывает падение напряжения на внутреннем сопротивлении базы $ r_{bb'}$ . Компонент $i_n$ является дробовым шумом постоянной составляющей тока базы и увеличивается как квадратный корень из коллекторного тока ( при постоянном коэффициенте бета ). Низкочастотный подъём вида 1/$ f $ серьёзно влияет на шумовой ток биполярных транзисторов, поэтому его вклад в общее напряжение шума можно увидеть в основном на низких частотах, причём, бывает, что только там он и виден. Более подробная модель биполярного транзистора позволит учесть этот эффект.

==485

Добавляя в формулу [8.18] шумового напряжения транзистора входной шумовой ток получаем \[ e_n^2=2qI_Cr_e^2+4kTr_{bb'}+ 2q\frac{I_C}{β_0}r_{bb'}\left(1+\frac{f_{ci}}{f} \right ) \qquad \mathrm{V^2/Hz}, \qquad [8.24] \] где как и прежде первое слагаемое может быть заменено на $ 2kT r_e$ , а частота точки перегиба графика $ f_{ci}$ растёт примерно как корень четвёртой степени из $I_C$ .

Чтобы понять, как компоненты шума взаимодействуют между собой, рассмотрим рис. 8.16 , где отдельно ( для каждого из трёх токов ) нарисованы графики $e_n$ от первых двух слагаемых ( пунктирная линия ), $e_n$ от третьего слагаемого ( тонкая сплошная линия ) и общее напряжение шума от всех компонентов уравнения [8.24] (жирная сплошная линия ). Это расчётные кривые, построенные для шумовых параметров типичного биполярного транзистора ( $β$ = 200 , $ r_{bb'}$ = 50 Ω , $ f_{ci}$ = 1 kHz при $I_C$=1 mA ).

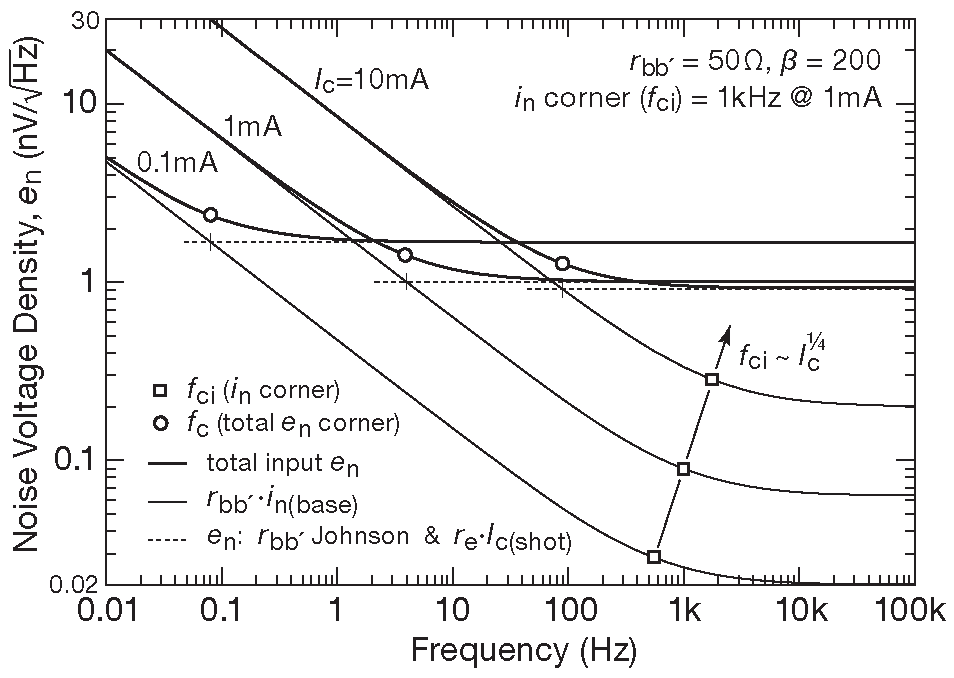
Рис.8.16 Расчётная частотная зависимость плотности ток биполярного транзистора ( см. уравнение [8.24] ) для условного транзистора с указанными на графике параметрами. Виден эффект от шумового ток $i_n$ на низких частотах и при больших токах коллектора

Рисунок показывает, что шумовая компонента $i_nr_{bb'}$ соперничает с двумя другими слагаемыми и вносит основной вклад при больших токах коллектора на низких частотах. Частота точки перегиба графика $ f_{ci}$ с ростом $I_C$ меняется довольно медленно, но зато вызывает сильное изменение точки перегиба результирующего графика $ f_c$ . Такой же эффект можно наблюдать на рис. 8.11 , но там приведена зависимость $e_n$ от тока коллектора с пучком кривых для нескольких характерных частот.

Чтобы сформировать целостное восприятие явления, отметим, что дополнительное напряжение шума проявляется только на очень низких частотах ( шкала на рис. 8.16 простирается вплоть до 0.01 Hz ! ) и относительно больших плотностях тока. Это не та причина, чтобы терять покой и сон ²² . На рис. 8.17 можно увидеть кривые шума, снятые для нескольких разных типов транзисторов. На частотах выше 10 Hz ( при изрядном токе коллектора 10 mA ) эффект хорошо заметен только у BC850 с его неприлично высоким значением $ r_{bb'}$ - порядка 750 Ω . Фактически у транзисторов с достаточно низким $ r_{bb'}$ снижение $e_n$ , получаемое за счёт высокого тока коллектора, больше, чем его повышение из-за низкочастотного подъёма дробового шума тока базы, как это видно из рис. 8.18 .

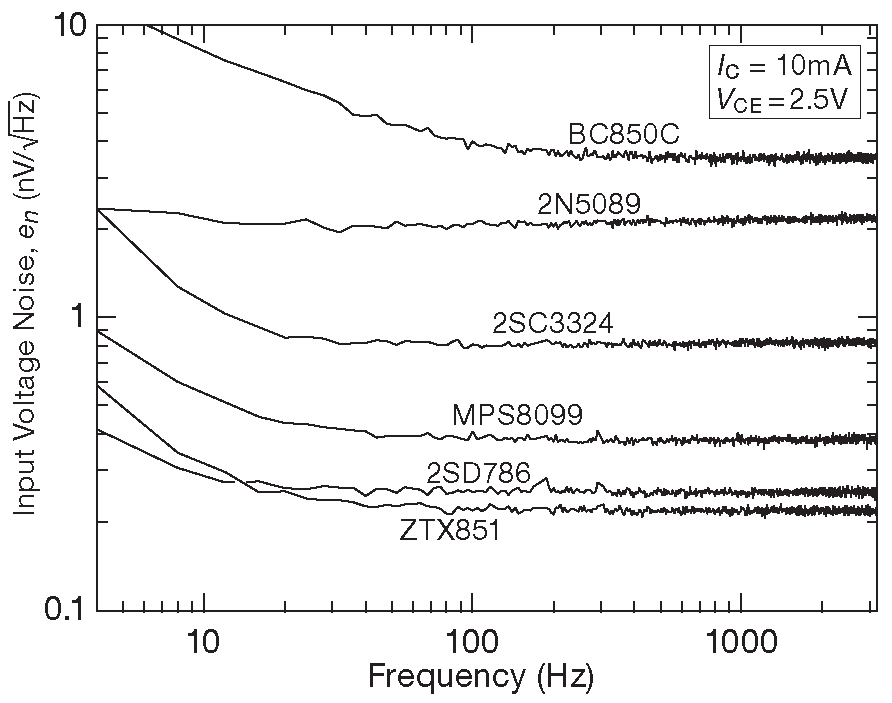
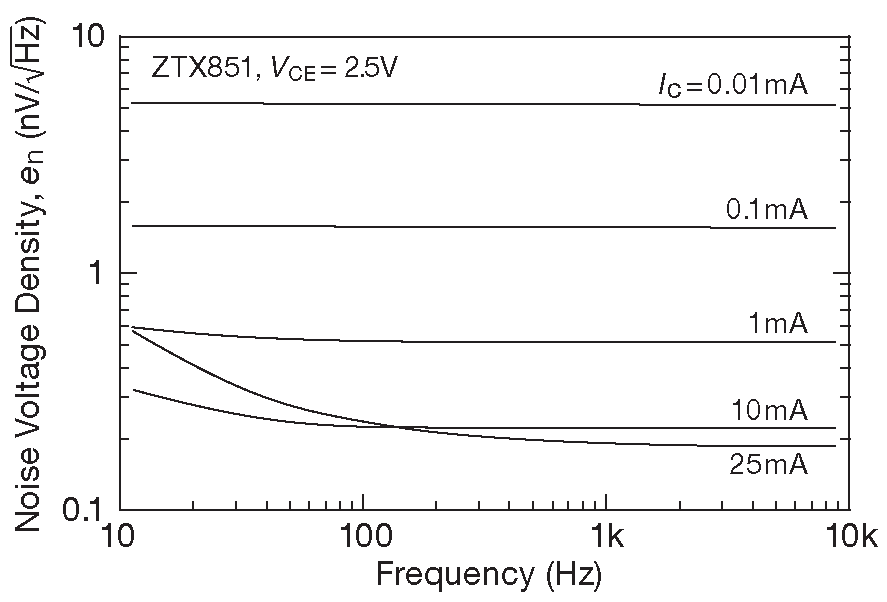
Рис.8.17 Спектр входного шума ( зависимость $e_n$ от частоты при $I_C$=10 mA ), измеренный для шести типов биполярных транзисторов с рис. 8.12
Рис.8.18 Спектр входного шума транзистора ZTX851 при пяти значениях ток коллектора. Шумовой ток базы увеличивает напряжение шума на низких частотах и больших токах, но до 10 mA выигрыш ещё есть

==486

8.3.4 Пример разработки: динамик в качестве микрофона

Применим полученные знания на практике и создадим простой и недорогой усилитель звуковой частоты, развязанный по постоянному току, с малым потреблением, однополярным напряжением питания +9V ( батарея или внешний блок питания ) и приведённым ко входу уровнем шума в несколько nV/$\sqrt{Hz}$ . Областью применения подобной схемы может быть переговорная система на входе, где небольшой динамик работает по совместительству микрофоном ²³ .

Чтобы удовлетворить шумовым требованиям задачи придётся подобрать из нескольких образцов динамик, чей выходной сигнал находится в диапазоне 30...100 μVrms , если говорить в него нормальным голосом. Хотелось бы добиться отношения сигнал-шум 40 dB или лучше, т.е. напряжение шума, отнесённое ко входу 0.5 μVrms или менее. Кроме того, желательно, чтобы стоимость компонентов была и в самом деле небольшой: цель разработки - уложиться в 25 центов.

Базовая схема

На рис. 8.19 изображена базовая схема каскада с общим эмиттером, связанного по переменному току ( эмиттерный резистор, шунтирован по высокой частоте ), который нагружен на эмиттерный повторитель. Искажения в данном случае не важны ( размах выходного напряжения должен составлять десятки милливольт для входного сигнала порядка 50 μV ), но очень желателен запас усиления по напряжению, и шунтирование резистора в цепи эмиттера исключает его из числа источников шума. В качестве исходного значения рабочего тока выберем 100 μA . Так же, как в ходе любой разработки, эта величина будет уточняться после получения первых результатов.

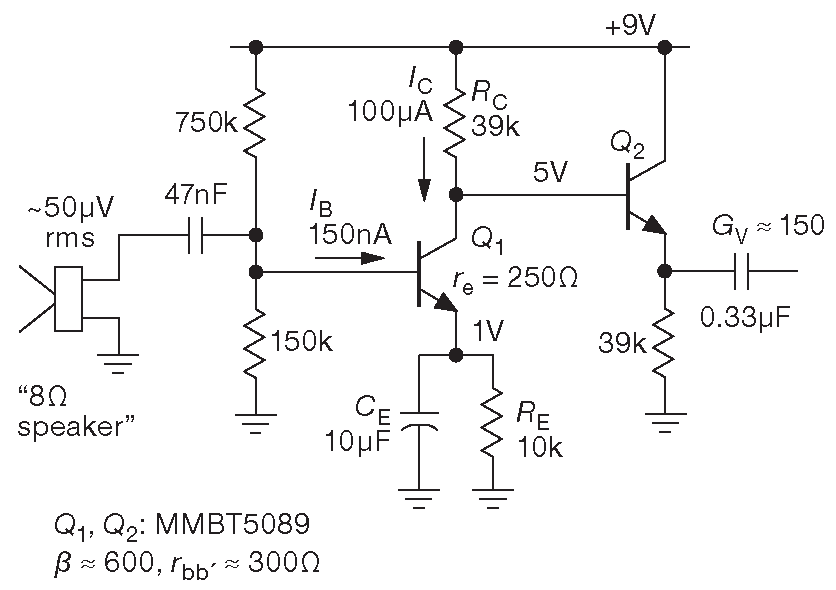
Рис.8.19 Малошумящий и недорогой предусилитель звуковой частоты, использующий звуковую головку в качестве источника сигнала

Расчёт шумов

Выбор 2N5089 в качестве рабочего обусловлен доступностью ( четыре различных производителя и полмиллиона штук на складах Digi-Key и Mouser ) и дешевизной ( $0.026 в партии 100 шт ). Кроме того, он позиционируется в качестве малошумящего ²⁴ . 2N5089 имеет большое усиление по току ( 400 min, 600 типовое значение при 100 μA ), но весьма высокое для «малошумящего» внутреннее сопротивление базы $ r_{bb'}$ ≈ 300 Ω .

Из уравнения [8.24] несложно посчитать вклад в плотность напряжения шума ( $e_n$ ) различных его компонент, приведённых ко входу ( RTI ) ( читателю рекомендуется повторить расчёты ):

Дробовый шум тока коллектора через $ r_e$	$ r_e\sqrt{2qI_C}$	1.4 nV/$\sqrt{Hz}$
Дробовый шум тока коллектора через $ r_e$
Тепловой шум $ r_{bb'}$	$\sqrt{4kTr_{bb'}}$	2.2 nV/$\sqrt{Hz}$
Тепловой шум $ r_{bb'}$
Тепловой шум $R_C$	$\sqrt{4kTR_C}/G_{V}$	0.17 nV/$\sqrt{Hz}$
Тепловой шум $R_C$
Дробовый шум $I_B$ через $ r_{bb'}$	$ r_{bb'}\sqrt{2qI_B}$	0.066 nV/$\sqrt{Hz}$
Дробовый шум $I_B$ через $ r_{bb'}$

==487

Основной вклад вносит тепловой шум внутреннего сопротивления базы, затем идёт дробовый шум тока коллектора, текущего через внутреннее сопротивление эмиттера $ r_e$ величиной 250 Ω при токе $I_C$=0.1 mA . Оставшиеся два слагаемых много меньше по величине: резистор в цепи коллектора $Q_1$ создаёт достаточно много теплового шума ( на выходе ), но отнесённый ко входу с учётом усиления по напряжению ∼150 , вносит незначительную долю в итоговую цифру. Ещё меньше вклад шумового напряжения, возникающего при прохождении дробового шумового тока базы через $ r_{bb'}$ . Есть и другие источники шума, но они несравнимы по величине. Скажем, ток теплового шума, создаваемого делителем и текущего через сопротивление динамика ( 8 Ω ), создаёт плотность шумового напряжения всего 0.003 nV/$\sqrt{Hz}$ .

Параметры

Из указанных плотностей напряжения шума можно получить общее среднеквадратическое напряжение шума в заданной полосе сигнала: $v_n=e_n\sqrt{Δ f}$=142 nVrms , где $e_n$ - общее значение плотности напряжения шума 2.6 nV/$\sqrt{Hz}$ , а $Δ f$ - ширина рабочей полосы ( в этом качестве взята «телефонная» полоса 3 kHz ). Если сравнить этот результат с 50 μVrms сигнала на входе, то отношение сигнал-шум составит 51 dB , что совсем не плохо за такую цену.

К слову сказать, стоимость компонентов - тоже одна из «характеристик». Беглое знакомство с ценами на SMT компоненты у четырёх поставщиков ( Digi-key, Mouser, Newark, Future ) даёт следующие результаты:

	в партии 100 шт.	в партии 1000 шт.

$Q_1,Q_2$	$0.026	$0.023
$ C_{in}$	$0.032	$0.012
$ C_E$	$0.068	$0.039
$ C_{out}$	$0.034	$0.017
резисторы	$0.012	$0.004

все компоненты	$0.246	$0.134

Возможные модификации

Получившееся в результате устройство превзошло целевые показатели технического задания, и разработку на этом можно было бы завершить, но всегда полезно возвратиться в исходную точку и посмотреть, что можно улучшить. В этом задании итоговое значение шума определяется довольно большим значением внутреннего сопротивления базы выбранного, с позволения сказать, «малошумящего» транзистора. Шумовые параметры можно было бы улучшить, выбрав в качестве входного транзистор с низким значением $ r_{bb'}$ . Возможных кандидатов можно взять из табл. 8.1a ( стр. 501 ) или на рис. 8.12 . Но как только тепловой шум $ r_{bb'}$ будет снижен, на первый план выйдет дробовый шум тока, текущего через внутреннее сопротивление эмиттера $ r_e$ и придётся увеличивать ток коллектора, чтобы выгадать ещё немного на $v_n$ ²⁵ . По рис. 8.12 видно, что при значениях тока, больших $I_C$=100 μA , параметры 2N5089 стремительно ухудшаются ( и даже не в два раза ) в сравнении с транзисторами с более низким значением $ r_{bb'}$ .

Можно зайти с другой стороны и отметить дешевизну и доступность MMBT5089, после чего снизить слегка ток коллектора ( скажем, до 50 μA ). Общий шум немного повысится: плотность увеличится с 2.6 до 3.0 nV/$\sqrt{Hz}$ , а SNR в звуковой полосе ухудшится на 1 dB ( с 50.9 до 49.8 dB ). Действие оправдано, если предполагается запитывать устройство от батарей.

8.3.5 Дробовый шум в источниках тока и эмиттерных повторителях

Как уже отмечалось ранее ( §8.1.2 ), в классическом источнике тока на биполярном транзисторе ( вновь приведённом на рис. 8.20 A ) дробовый шум подавляется. В первый момент данный факт кажется очевидным, потому что коллекторный ток равен эмиттерному ( за исключением небольшой добавки от тока базы ), а в эмиттерном дробовый шум отсутствует ( это утверждение верно для всех металлических проводников ). Но в то же время коллектор представляет собой тот вид диффузных барьеров, в которых дробовый шум обусловлен физикой процесса.

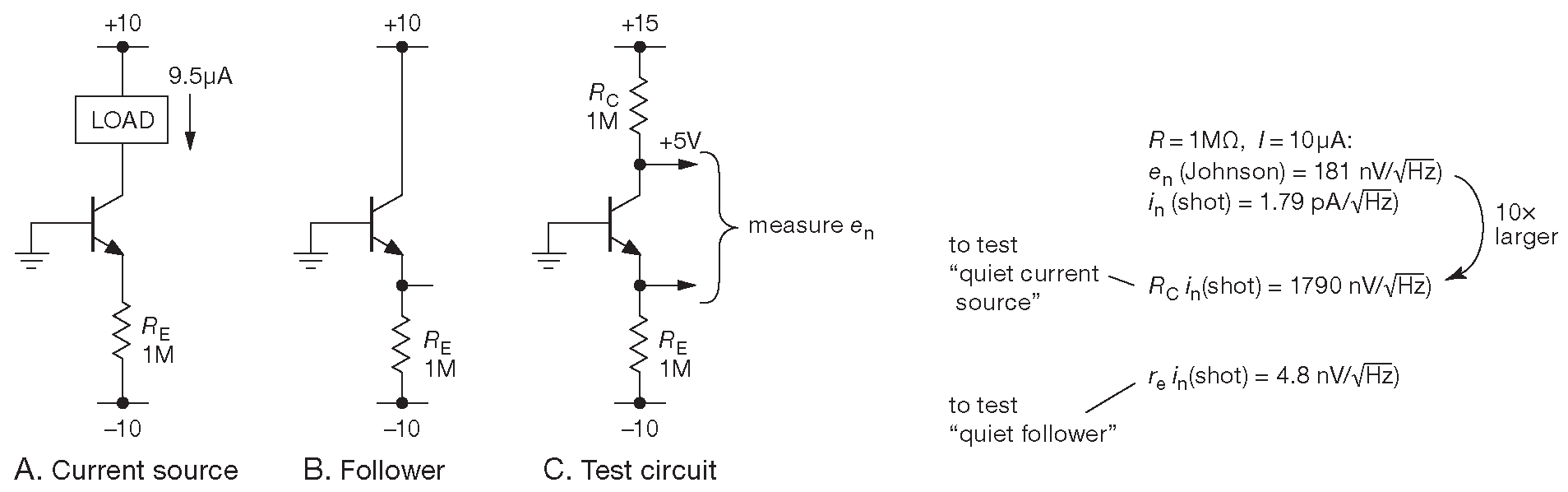
Рис.8.20 Дробовый шум отсутствует в источнике тока на биполярном транзисторе (A), но имеется в эмиттерном повторителе (B), что легко проверить, измерив плотность напряжения шума по схеме (C)

Ну и ладно, пусть источник тока создаёт дробовый шум, но на эмиттерном-то терминале ток чист и тих ( а значит, нет и шумового напряжения ). Сейчас как посмотрим сигнал на резисторе!

Рассуждение не верно. Дела обстоят ровно наоборот, и «тихим» является именно вывод источника тока, а на выходе эмиттерного повторителя присутствует шумовое напряжение в точности равное дробовому шуму тока коллектора, текущему через $ r_e$ , а именно, $ r_e\sqrt{2qI_C}$ , который имеется в уравнении [8.24] ²⁶ .

Это довольно легко проверить. Подключим к источнику тока 10 μA нагрузку в виде коллекторного резистора номиналом 1 MΩ ( рис. 8.20C ). В отсутствии дробового шума $I_C$ на коллекторе будет виден только тепловой шум плотностью 181 nV/$\sqrt{Hz}$ ²⁷ , или, если дробовый шум $i_n=\sqrt{2q I_C}$ всё же присутствует, то шумовой сигнал будет в десять раз больше. Между тем на эмиттере, указанный дробовый шум, проходя через $ r_e$ , будет создавать напряжение шума плотностью 4.8 nV/$\sqrt{Hz}$ , а если дробовый шум эмиттера отсутствует, выход повторителя будет тихим ( в отличие от других источников шума биполярного транзистора в соответствии с уравнением [8.24] ).

==488

Итак, схема C собрана, и.. ( барабанная дробь ) .. измеренное шумовое напряжение на коллекторе 190 nV/$\sqrt{Hz}$ ( что соответствует величине теплового шума, т.е. источник тока молчит ), а на эмиттере - 4.93 nV/$\sqrt{Hz}$ ( что согласуется с величиной дробового шума тока коллектора, проходящего через $ r_e$ ) . Очевидно, дробовый шум отсутствует в источнике тока, но имеется на выходе повторителя. Интересно! Проверить, что в коллекторном токе нет дробового шума можно ещё одним способом: надо добавить шунтирующий конденсатор между выводами базы и эмиттера. Напряжение шума на коллекторе подскакивает до 1679 nV/$\sqrt{Hz}$ в полном согласии с рассчитанным по формуле значением 1664 nV/$\sqrt{Hz}$ ²⁸ . Как это всё понимать?

Чтобы решить головоломку, надо начать с безусловно правильных утверждений и посмотреть, что из них следует. Рассмотрим рис. 8.21 шаг за шагом.

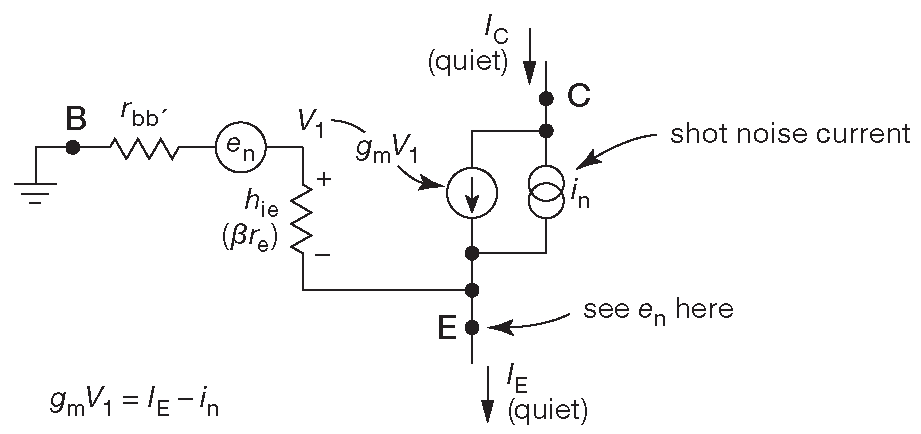
Рис.8.21 Упрощённая трёхвыводная гибридная «π-модель» источника тока - эмиттерного повторителя с рис. 8.20C . Напряжение шума $e_n$ просто следствие неустранимого внутреннего дробового шумового тока $i_n$ . Если эмиттерный ток не шумит, то не будет шуметь и ток коллектора $I_C$

Совершенно определённо известно, что ток эмиттера не шумит, потому что это ток в металлическом проводнике. Значит, беспокоиться следует о возможном зашумлении тока эмиттера за счёт флуктуаций напряжения база-эмиттер ( т.е. входном шумовом напряжении ), борьба с которым достаточно очевидна. Эффект можно снизить так сильно, как это требуется ( он, правда, и так уже незначителен, т.е. колебания $v_{n( BE )}$ имеет порядок микровольт ). Для этого надо просто одновременно и пропорционально увеличить $R_E$ и потенциал отрицательной шины питания.
Где-то в кристалле транзистора должен течь диффузный ток коллектора, который как раз является источником классического некоррелированного дробового шума $i_n=\sqrt{2qI_{C(dc)}}$ , который транзистором не регулируется.
Но речь идёт о транзисторе с большой бетой ( для упрощения рассуждений ), т.е. о трёхвыводном компоненте с пренебрежимо малым током базы. Это значит, что ток, втекающий в коллекторный вывод, равен току, вытекающему из эмиттерного вывода, а этот последний сам не шумит.
Значит должно существовать явление, благодаря которому некоторая часть тока коллектора меняется точно в пропорции, необходимой для компенсации колебания дробового шума.

Чтобы дело обстояло именно таким образом, входное напряжение в модели проводимости биполярного транзистора должно соответствовать следующему соотношению: $ g_m V_1=I_E - i_n$ , т.е. часть напряжения $ V_1$ , соответствующая входному шумовому напряжению равна \[ e_n = -i_n/g_m , \qquad \qquad [8.25] \] т.е. ( если вспомнить, что $ r_e$=1/$ g_m$ ) имеет знакомую по уравнению [8.24] форму $i_n r_e$ .

На первый взгляд эти соотношения выглядят как кольцевая ссылка, но на самом деле они показывают, откуда именно возникает шум перехода база-эмиттер. Эта строка доказательства также хорошо объясняет присутствие шумового напряжения $e_n$ на эмиттере в тестовой конфигурации ( и, конечно, на выходе эмиттерного повторителя и на входе усилителя с общим эмиттером и т.д. ). Кроме того, такие рассуждения объясняют, почему конденсатор, повешенный на вывод эмиттера, снижает полный дробовый шум коллектора в источнике тока: такое изменение схемы выключает из рассуждений пункт #1 , потому что на частоте сигнала конденсатор полностью блокирует ток через эмиттерный резистор. Фактически схема превращается в повторитель с заземлённым эмиттером ( из исходного источника тока или повторителя ), в котором напряжение входного шума, из уравнения [8.25] усиливается проводимостью $ g_m$ и превращается в выходной токовый шум эквивалентный $ g_m e_n$ . Это тот самый полный ( не отфильтрованный ) дробовый шум, соответствующий постоянному току коллектора $I_C$ (шаг #2 из рассуждений выше ), который измеряется в тестовой схеме.

==489

Последнее ( важное ) замечание: для подавления дробового шума источника тока требуется тихий приёмник тока эмиттера. В тестовой схеме его функции выполняет большой ( по сравнению с $ r_e$ ) нагрузочный резистор $R_E$ ( в данном случае 1 MΩ в сравнении с 2.5 kΩ ). Но его можно поставить только в примитивном ( классическом ) генераторе тока, а использовать такой подход в более сложных схемах не получится. Данная проблема ставит вопрос о величине $R_E$ , которая будет считаться «большой» в указанном значении.

Решить его довольно легко: на эмиттере присутствует напряжение шума $e_n$ , соответствующее тепловому шума резистора с номиналом $ r_e$/2 и импедансом источника $ r_e$ , т.е. шум соответствует тепловому шуму резистора номиналом 2$ r_e$ . Оно ослабляется тихим ( т.е. свободным от дробового шума ) резистором подтяжки $R_E$ . В результате коэффициент подавления шума тока коллектора составляет $\sqrt{2r_e/R_E}$ . Например, при токе коллектора 1 mA импеданс эмиттера $ r_e$=25 Ω , напряжение шума соответствует шуму резистора номиналом 12.5 Ω или эквивалент токового шума резистора 50 Ω . Тогда резистор $R_E$ номиналом 50 Ω уменьшает шум на 3 dB , резистор 4.95 kΩ - на 20 dB , и т.д. В более общем виде, уменьшение шума тока коллектора $i_n$ происходит в пропорции $\sqrt{50 mV/V_{R_E}}$ , где $ V_{R_E}$ – падение напряжения на резисторе подтяжки $R_E$ .

==489

¹⁵ Есть ещё одно слагаемое, которое становится заметным на больших частотах или при малом шумовом токе $i_n$ - дополнительный ток перезаряда входной ёмкости шумовым напряжением: $i_n=e_nωC_{in}$ , см. §8.11.3 и §X4.3.4 . <-

¹⁶ 2SD786 много лет был стандартом, на который равнялись все малошумящие транзисторы. Он упоминается здесь, потому что подробно описан, по нему есть масса данных, и его характеристики превосходны. Преемником можно назначить ZTX851 ( комплементарный pnp - ZTX951 ). Он описывается и используется в примерах далее в этой части. <-

¹⁷ Строго говоря, «сопротивления» $ r_e$ не существует. Вместо него имеется обратная проводимость транзистора $ r_e = v_b/i_c$=1/$ g_m$ или изменение напряжения на базе, вызванное изменением тока коллектора. На самом деле это просто общепринятый способ описания, но «резисторную» аналогию следует использовать с оглядкой: речь идёт об идеальном сопротивлении, не имеющем теплового шума. <-

¹⁸ См. §8.3.5 где этот тонкий вопрос разбирается подробного. <-

¹⁹ Эффективное значение $ r_{bb'}$ склонно к небольшому увеличению при малых токах. Например, дополнительный шум (5.9 nV/$\sqrt{Hz}$ вместо 4.5 nV/$\sqrt{Hz}$ ) при 10 μA у 2N5089 появляется именно из-за изменения $ r_{bb'}$ . Расчёты показывают, что сопротивление увеличивается с 290 Ω при 10 mA до где-то 900 Ω при 10 μA ( т.е. при изменении тока на три порядка ) или пропорционально $ (I_C )^{-1/6}$ ( SPICE модель шума транзистора учитывает этот эффект ). <-

²⁰ Основную сложность представляет рост $i_n$ с увеличением температуры и со снижением частоты ( по закону 1/$ f $ ). <-

²¹ Отметим, что идеальный конденсатор ( или индуктивность ) не создаёт теплового шума. <-

²² Но если сон и аппетит из-за «проблемы 1/$ f $» в малошумящем усилителе с большим током коллектора таки потеряны, то на этот случай есть красивый приём: надо включить пару транзисторов так, чтобы их шумы вида 1/$ f $ компенсировали друг друга. См. Broderson, Chenette, and Jaeger, “A superior low-noise amplifier”, 1970 (IEEE ISSCC, p. 164 ). Способ позволяет достичь пятикратного подавления низкочастотного шума, а платой за это будет увеличение на 3 dB более высокочастотной компоненты $e_n$ ( белого шума ). <-

²³ Для читателей, сомневающихся, что «стены имеют уши», данная схема может подсказать интересную тему для размышления. <-

²⁴ В частности Onsemi прямо говорит: «малошумящий транзистор», Fairchild и NXP относят его к компонентам общего назначения, но характеризуют как пригодные для «малошумящих схем с большим усилением общего назначения» и «для входных каскадов с малым уровнем шума звуковоспроизводящей аппаратуры» соответственно. <-

²⁵ Сколь далеко можно продвинуться в этом направлении видно из темы «экстремальные исследования» в §8.5.9 . <-

²⁶ К которому ещё надо прибавить тепловой шум и дробовый шум тока базы через $ r_{bb'}$ . <-

²⁷ Это значение в $\sqrt{2}$ раз больше, чем тепловой шум резистора 1 MΩ , и составляет 128 nV/$\sqrt{Hz}$ . Множитель $\sqrt{2}$ возникает из-за того, что транзистор включён по схеме инвертора с единичным коэффициентом усиления, $R_E$ ( тоже 1 MΩ ) вносит такой же по величине шум, не согласованный с шумом нагрузки. <-

²⁸ Для эксперимента использовалась схема с батарейным питанием и током коллектора 8.65 μA . Отсюда и чуть меньшие расчётные значения дробового шума. <-

Дробовый шум тока коллектора через \( r_e\)	\( r_e\sqrt{2qI_C}\)	1.4 nV/\(\sqrt{Hz}\)
Дробовый шум тока коллектора через \( r_e\)
Тепловой шум \( r_{bb'}\)	\(\sqrt{4kTr_{bb'}}\)	2.2 nV/\(\sqrt{Hz}\)
Тепловой шум \( r_{bb'}\)
Тепловой шум \(R_C\)	\(\sqrt{4kTR_C}/G_{V}\)	0.17 nV/\(\sqrt{Hz}\)
Тепловой шум \(R_C\)
Дробовый шум \(I_B\) через \( r_{bb'}\)	\( r_{bb'}\sqrt{2qI_B}\)	0.066 nV/\(\sqrt{Hz}\)
Дробовый шум \(I_B\) через \( r_{bb'}\)

	в партии 100 шт.	в партии 1000 шт.

\(Q_1,Q_2\)	$0.026	$0.023
\( C_{in}\)	$0.032	$0.012
\( C_E\)	$0.068	$0.039
\( C_{out}\)	$0.034	$0.017
резисторы	$0.012	$0.004

все компоненты	$0.246	$0.134