8.4 Нахождение en по данным о коэффициенте шума
==489
Традиционные паспортные данные на транзисторы содержали некоторые табличные значения для \(e_n\) и ( часто ) графики зависимости \(e_n\) и \(i_n\) от частоты при некоторых значениях тока ( или зависимость \(e_n\) и \(i_n\) от тока коллектора на некоторых частотах ), как у уже приводившихся справочных данных на 2SD786 и MPSA18.
Так вот, это всё было! Теперь в справочных данных приводят табличные данные и графики для коэффициента шума (NF) . Например, на рис. 8.22 изображены контурные кривые равных значений NF в зависимости от \(I_C\) и \(R_S\) для малошумящего биполярного npn транзистора 2SC3324 фирмы Toshiba 29 .
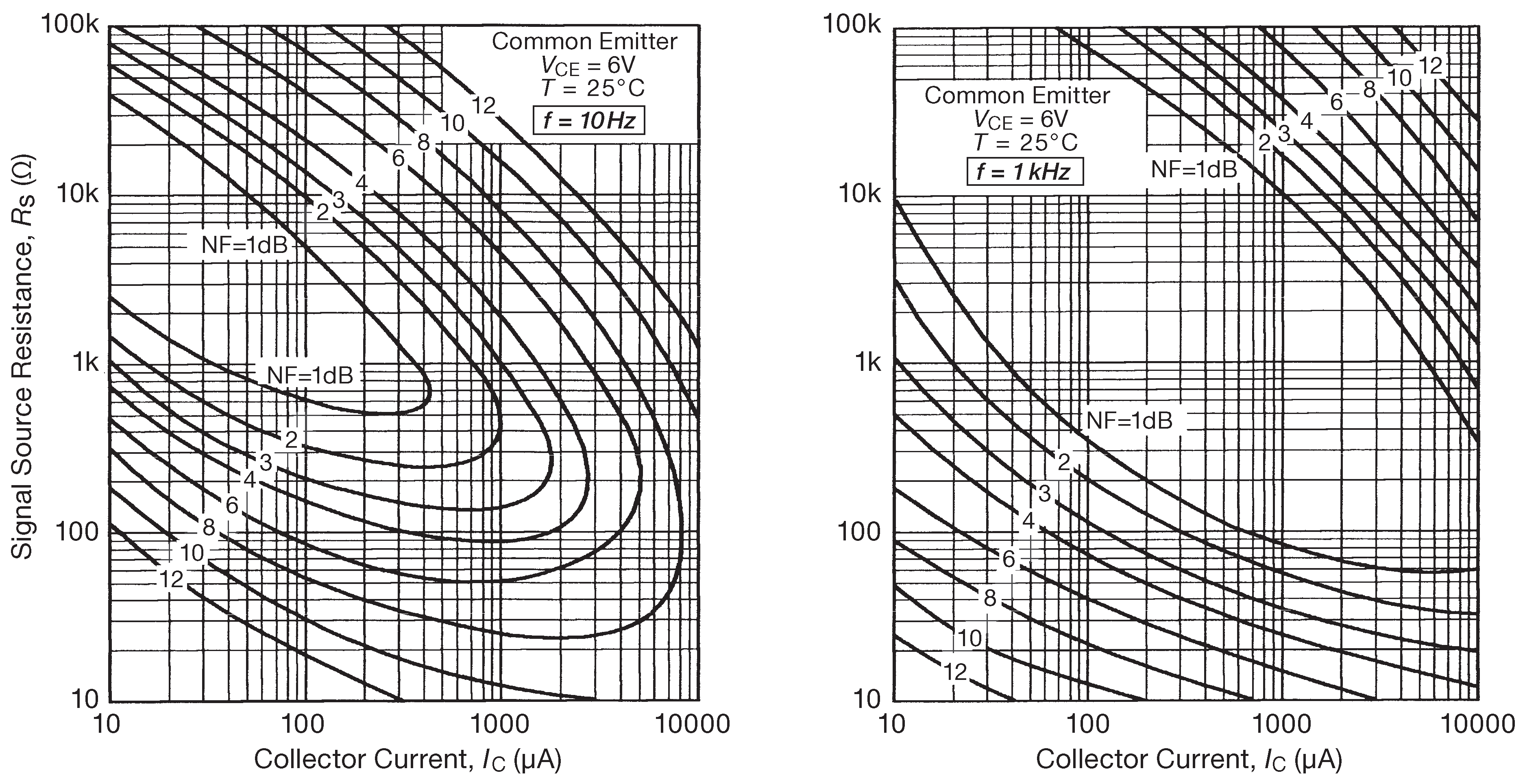
Рис.8.22 В паспортных данных на малошумящий npn транзистор 2SC3324 фирмы Toshiba нет табличных или графических данных по входному напряжению шумов \(e_n\) . Вместо них приводятся вот такие изображения зависимости коэффициента шума NF от тока коллектора и импеданса источника
Оба графика содержат массу информации, хотя и построены всего для двух частот - 10 Hz и 1 kHz , и было бы очень приятно увидеть график зависимости параметров шума от частоты. Посмотрим, что можно выжать из этих картинок.
8.4.1 Шаг 1: зависимость NF от IC
Построить зависимость NF от тока коллектора для каждого сопротивления источников из имеющегося набора можно, просто двигаясь вдоль горизонтальной линии рис. 8.22 и отсчитывая значения параметра. Очень удобно использовать какую-либо электронную таблицу с возможностью графического вывода, подобную Microsoft Excel или ( если есть желание показать результаты ) более сложные математические пакеты, типа MATHLAB® или Mathematica®. Рис. 8.23 показывает, что можно получить, если считывать данные графика для частоты 1 kHz с рис. 8.22 при шести значениях импеданса источника. Будем считывать цифры коэффициента шума для шагов шириной в половину декады \(I_C\) ( т.е. 10 μA, 30 μA, 100 μA и т.д. ), заносить их в Excel, а получившуюся ломанную сгладили с помощью кривых Безье в Adobe Illustrator®. Значения коэффициента шума ниже 1 dB следует считать недостоверными, потому что на рис. 8.22 , откуда взяты данные, нет контуров для значений NF меньших, чем 1 dB 30 . Пунктирная линия обозначает уровень NF=3 dB , при котором транзистор вносит шум эквивалентный тепловому шуму сопротивления источника.
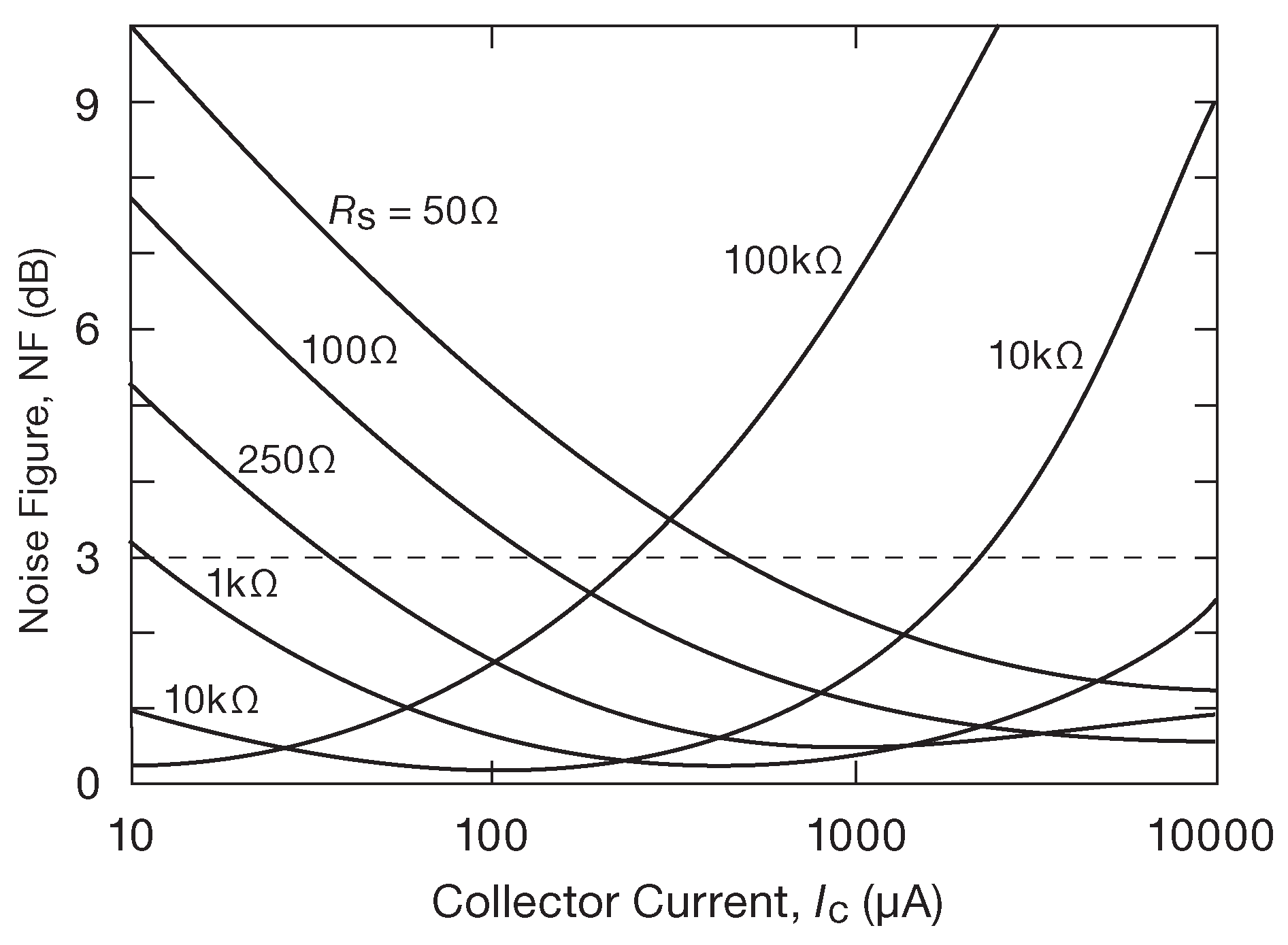
Рис.8.23 Зависимость коэффициента шума транзистора 2SC3324 от тока коллектора, построенная по данным с рис. 8.22
Перед тем, как двигаться дальше, рассмотрим эти графики ещё раз. Для малых величин \(R_S\) напряжение теплового шума источника невелико - немного меньше, чем входное напряжение шума \(e_n\) при малых токах коллектора 31 . Например, для \(R_S\) =100 Ω величина составит \(e_n\) =1.3 nV/\(\sqrt{Hz}\) . Именно поэтому коэффициент шума улучшается с увеличением тока коллектора. С другой стороны, для больших величин \(R_S\) напряжение шума транзистора совершенно незначительно в сравнении с тепловым шумом резистора. Зато при работе с приличными токами коллектора входной токовый шум транзистора ( дробовый шум тока базы \(i_n≈\sqrt{2qI_B}\) ) создаёт столь большое падение напряжения на \(R_S\) , что оно становится гораздо заметнее, чем тепловой шум того же \(R_S\) . Именно поэтому графики коэффициента шума проходят выше ( значения не так хороши ).
8.4.2 Шаг 2: зависимость NF от RS
Рис. 8.24 демонстрирует похожую зависимость, но на этот раз коэффициента шума от сопротивления источника ( вместо \(I_C\) ) для каждого отдельного значения тока. Графики построены по тем же данным для частоты 1 kHz с рис. 8.22 , только на этот раз значения считываются по вертикали, соответствующей конкретному значению тока коллектора. Такой вариант удобнее для определения оптимального диапазона рабочих токов для сигнала от источника с заданным импедансом
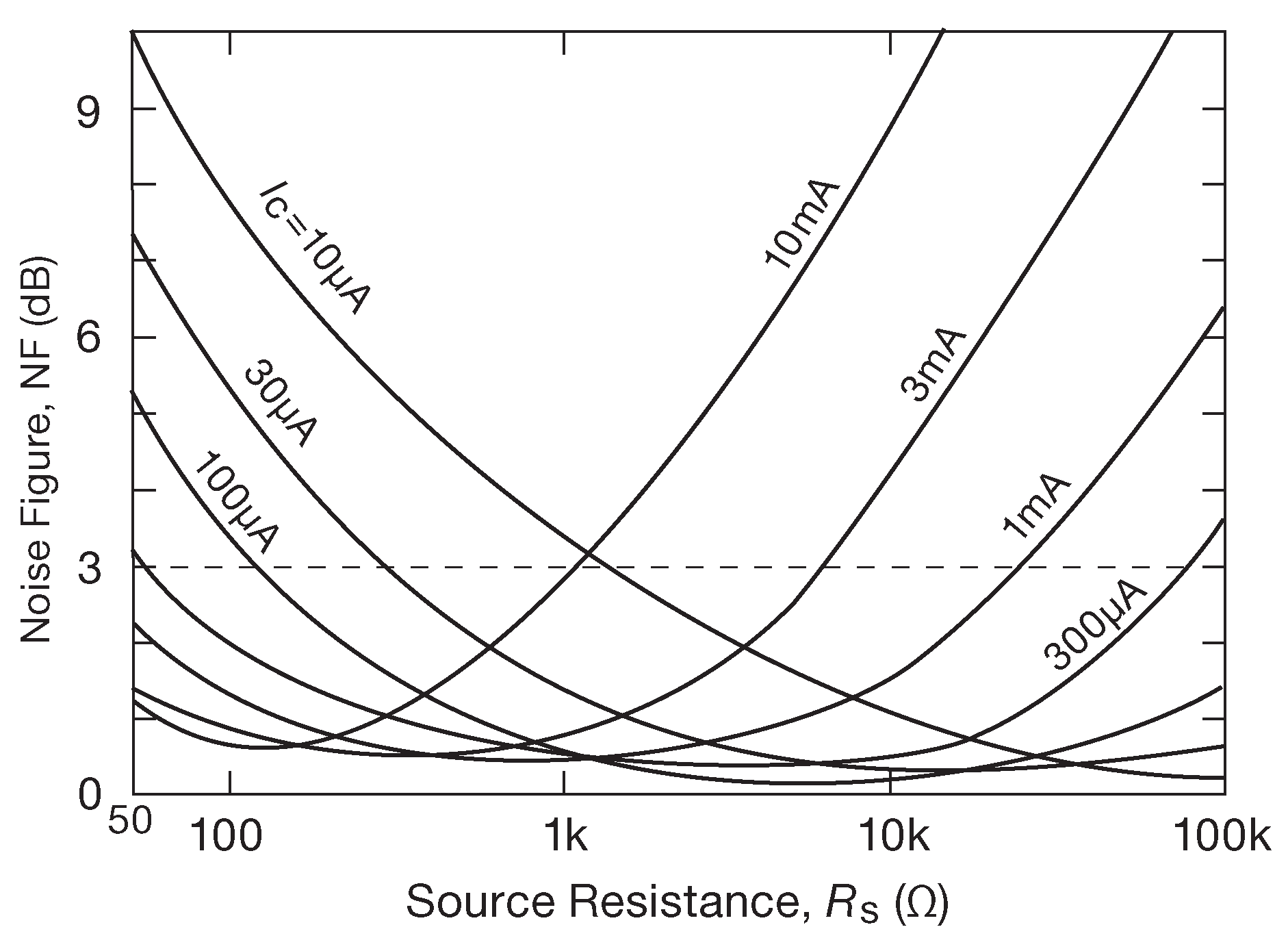
Рис.8.24 Зависимость коэффициента шума транзистора 2SC3324 от импеданса источника, построенная по данным с рис. 8.22
==490
8.4.3 Шаг 3: получение en
Два предыдущих рисунка ( NF от \(I_C\) и NF от \(R_S\) ) являются не чем иным, как простой реорганизацией паспортных данных ( рис. 8.22 ), не требующей каких бы то ни было вычислений.
С напряжением шума \(e_n\) ситуация иная. Теперь требуется вычислить соотношение, обратное уравнению [8.13] , чтобы получить \(e_n\) из данных по NF : \[ e_n=\sqrt{4kTR_S} \sqrt{10^{[\mathrm{NF}/10]}-1} \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.26] \]
Первый множитель - плотность теплового шума источника, второй – составная величина, учитывающая различные компоненты шума транзистора. Второй сомножитель включает доли от и от \(e_n\) , и от \(i_n\) , поэтому для низких значений сопротивлений источника необходимо использовать цифры NF , т.к. вклад от токовой составляющей \(i_n\) пренебрежимо мал 32 .
==491
На графике 8.25 видна зависимость \(e_n\) от тока коллектора, начинающаяся с коэффициента шума для импеданса источника \(R_S\) =50 Ω ( рис. 8.22 и 8.23 ). Подобно всем прочим, выбранный транзистор демонстрирует рост уже знакомого фликкер-шума с подъёмом 1/\( f \) ниже частоты точки перегиба графика ( см. §8.1.3 и §5.10.6 ).
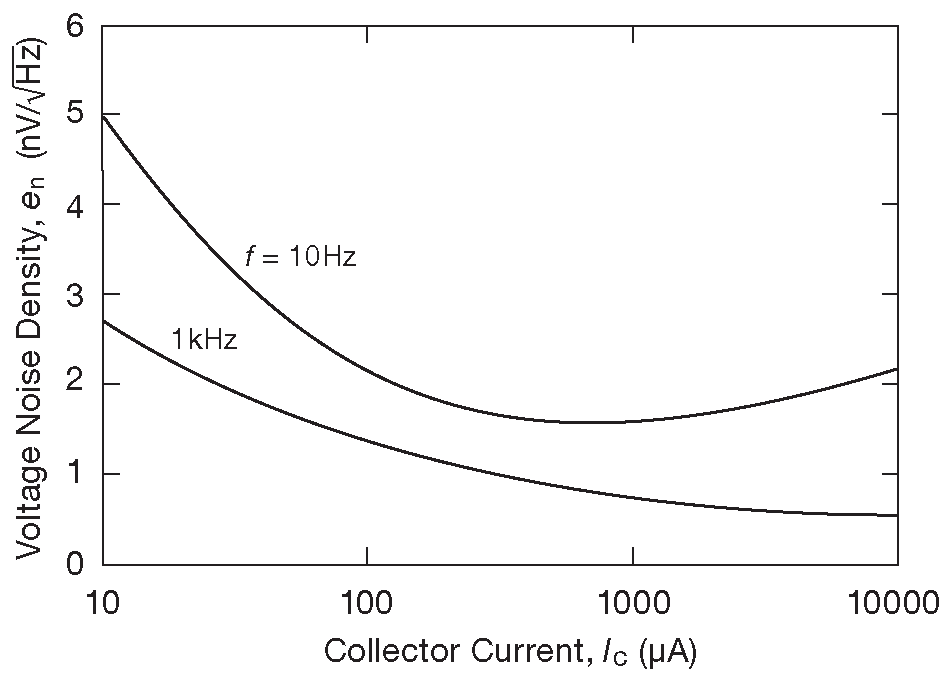
Рис.8.25 Зависимость напряжения шума 2SC3324 от тока коллектора, полученная по данным рис. 8.22
8.4.4 Шаг 4: спектр en
Ранее уже объяснялось отсутствие данных по зависимости шума от частоты: они даются только для частот 10 Hz и 1 kHz , но этот пробел можно заполнить. С разумной степенью точности можно рассчитывать, что мощность шума на низких частотах растёт по закону 1/\( f \) ( т.е. \(e_n ∝\) 1/\(\sqrt{f}\) ) , и две имеющиеся точки охватывают частоту перегиба 1/\( f \) .
Чтобы восполнить пробел, надо определить \( f_c\) - частоту перегиба графика 1/\( f \) по данным о \(e_n\) , в который она входит. Хорошим приближением будет соотношение: \[ f_c=f_{L}\left(\frac{e_{nL}^2}{e_{nH}^2}-1\right ), \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.27] \]
где \(e_{nL}\) - плотность шума на частоте \( f_{L}\) ниже частоты точки перегиба, а \(e_{nH}\) - плотность шума сильно выше точки перегиба ( см. обсуждение на стр. 566 ). Выяснив \( f_c\) , можно найти зависимость \(e_n\) от частоты: \[ e_n( f)=e_{nH}\sqrt{1+( f_c/f)} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad [8.28] \]
Так как частота точек перегиба зависит от тока коллектора, значения \(e_{nL}\) и \(e_{nH}\) берутся из графика 8.25 для каждой из четырёх декад величины \(I_C\) , после чего строится зависимость \(e_n\) от частоты. Итоговый спектр напряжения шумов можно увидеть на рис. 8.26 .
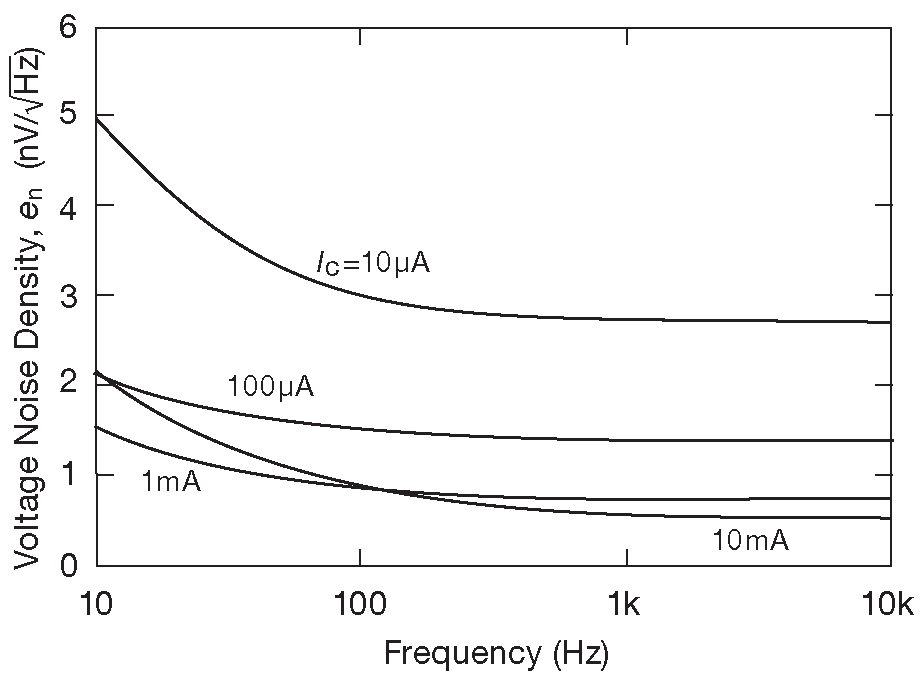
Рис.8.26 Зависимости напряжения шума 2SC3324 от частоты, по данным с рис. 8.25
8.4.5 Шаг 5: спектр in
Построение зависимости шумового тока \(i_n\) от частоты происходит аналогично. Выше точки перегиба будет виден дробовый шум тока базы ( \(i_n=\sqrt{2qI_B}\) ) , возрастающий по закону 1/\( f \) на низких частотах.
После того, как построены зависимости \(e_n\) и \(i_n\) от частоты, можно утверждать, что из контурных карт коэффициента шума извлечена вся информация. Если заглянуть чуть дальше ( §8.9.1.E и рис. 8.58 ), то можно увидеть, как по \(e_n\) и \(i_n\) можно предсказать зависимость плотности действующего значения общего шума от сопротивления источника. Схема в верхнем левом углу рисунка показывает простой и удобный способ поиска точек, разделяющих области с доминированием \(e_n\) ( с низким \(R_S\) ) , теплового шума ( со средним \(R_S\) ) и \(i_n\) ( с высоким \(R_S\) ) . \(e_n\) и \(i_n\) будут активно использоваться на протяжении всей этой части книги.
8.4.6 Что делать, если рабочий ток выбрать нельзя
Знание того, как \(e_n\) и \(i_n\) меняются с изменением тока коллектора ( или стока ) помогает установить рабочую точку с оптимальным соотношением шума, как будет ясно из следующего параграфа. Но иногда выбор рабочего тока делает кто-то со стороны и разработчику приходится довольствоваться тем, что есть. На рис. 8.27 приведён пример контурной карты коэффициента шума для предусилителя SR560 фирмы Stanford Research Systems ( §8.6.4 ). По высокому входному сопротивлению ( ∼200 kΩ ) понятно, что на входе стоят полевые транзисторы, и для источника с низким импедансом шумовые характеристики будут далеки от оптимальных: NF=15 dB для \(R_S\) =50 Ω ! Сравните с ∼2 dB коэффициента шума транзистора 2SC3324 при токе \(I_C\)=5 mA .
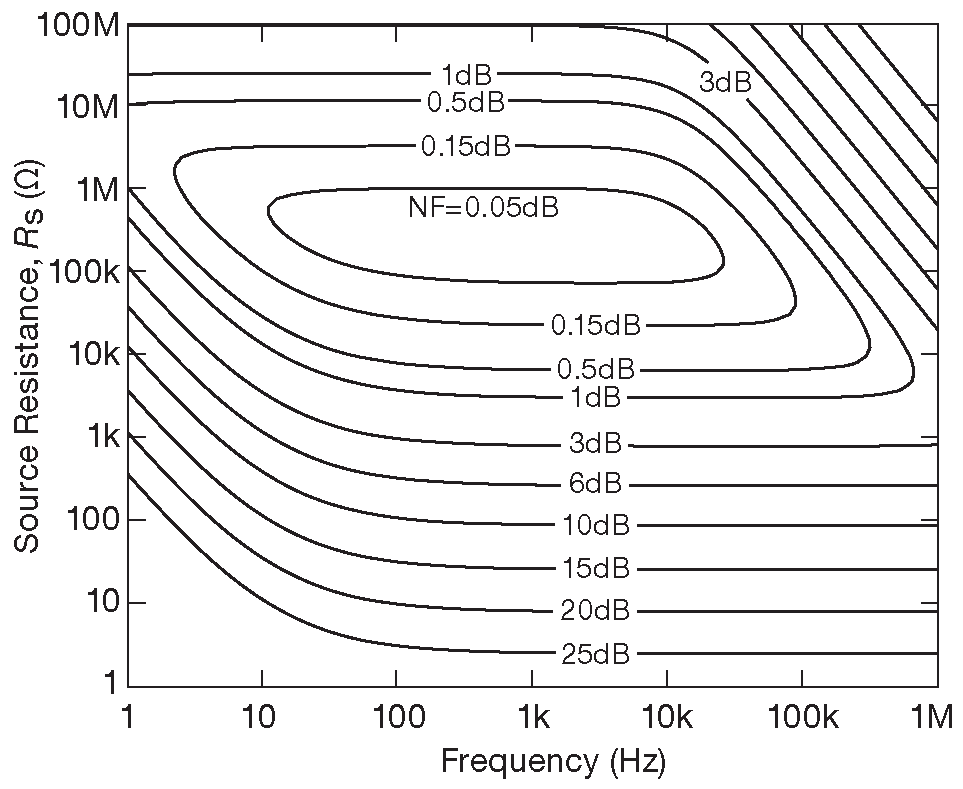
Рис.8.27 Контурная карта коэффициента шума усилителя SR560 в зависимости от частоты и сопротивления источника ( с разрешения Stanford Research Systems )
==492
Чего делать НЕ НАДО
Отлично, думаете вы, поставим последовательно с источником резистор 200 kΩ и - вуаля! - получаем коэффициент шума 0.05 dB .
НЕТ, НЕ ПОЛУЧАЕМ! В результате в схеме просто появится масса дополнительного теплового шума от резистора, который забьёт шум усилителя. Приборы с указанными параметрами оптимизированы для источников сигнала с высоким импедансом и далеки от идеала в 50-омных системах. А вот что МОЖНО сделать, если всё же нужно работать с низкоомным сигналом, так это увеличить импеданс источника с помощью сигнального трансформатора. Подойдёт что-либо подобное North Hills HB0904 ( 50 Ω : 1200 Ω , рабочая полоса 1 kHz...6 MHz ) или Mini-Circuits T16-6T-X65 ( 50 Ω : 800 Ω , рабочая полоса 30 kHz...75 MHz ). Трансформатор позволит вписаться в зону с коэффициентом шума ∼3 dB , что много лучше, чем NF=15 dB для прямого подключения к 50-омному источнику. Сигнальные трансформаторы рассматриваются в §8.10 [* и в §H.2.3 ] .
==492
29 Парным к нему pnp является 2SA1312. <-
30 В паспортных данных среди табличных данных можно обнаружить цифры 0.2 dB ( типовое значение ) на 1 kHz , при токе коллектора 100 μA и импедансе источника 10 kΩ , т.е. том наборе условий, при котором точка попадает в самый центр набора контуров. Правда, в справочных данных приводится и значение для наихудшего случая - NF=3 dB , поэтому, если и в самом деле понадобится именно цифра NF=0.2 dB , то придётся заняться поиском жемчуга в куче транзисторов. <-
31 Стоит напомнить, что эта последняя величина приблизительно равна падению напряжения при протекании дробового шума тока коллектора через сопротивление эмиттера ( \( r_e\) ) : \(e_n ≈ \sqrt{2qI_C} · (kT/qI_C) \) , что равно тепловому шуму воображаемого резистора \(R=r_e\)/2 , который в свою очередь равен 100 Ω при токе \(I_C\)=125 μA . Таким образом, \(e_n\) транзистора связано с током коллектора зависимостью \(e_n ∝\) 1/\(\sqrt{I_C}\) . <-
32 Аналогично, для больших значений сопротивления можно брать данные только по \(i_n\) , т.к. доля \(e_n\) незначительна. <-

