8.13 Ограничение рабочей полосы и измерение среднеквадратического напряжения

==561

8.13.1 Ограничения рабочей полосы

Все измерения, о которых здесь идёт речь, предполагают, что рассматривается шум только в ограниченной полосе частот. В некоторых случаях такое ограничение может обеспечить сам усилитель, если же это не так, то придётся поставить у него на выходе какой-либо фильтр.

RC фильтр

Самый очевидный вариант - использовать простой ФНЧ ( или полосовой фильтр ), частота $ f_{3db}\space$ которого подобрана под нужную рабочую полосу. Для точного измерения шума надо знать «эквивалентную полосу шума» ( ENBW ), т.е. полосу идеального фильтра [* с вертикальной заграждающей характеристикой] , через который пройдёт такое же напряжение шума ( рис. 8.96 ). Именно эта эквивалентная частота должна использоваться в качестве параметра «BW» в формулах. Математические выкладки не так сложны и для RC ФНЧ дают: \[ BW=\frac{π}{2}f_{3dB}= 1.57f_{3dB} \qquad [8.55]. \]

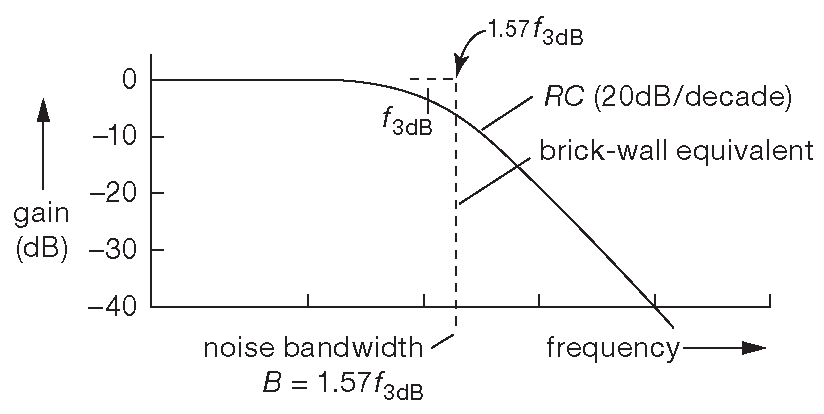
Рис.8.96 Эквивалентная шумовая полоса идеального фильтра, соответствующего RC ФНЧ

Для пары последовательных RC секций ФНЧ ( буферированных, чтобы они не нагружали друг друга ), магическое соотношение изменяется: BW=1.22×$ f_{3db}$ . Для ФНЧ Баттерворта, рассматривавшихся в §6.2.6 и §6.3.2 , шумовая полоса выражается следующими соотношениями: \[ \begin{align*} BW &= 1.57f_{3dB} = \frac{1}{4RC} &(1 pole ),\\ BW &= 1.11f_{3dB} ≈ \frac{1}{5.6RC} &( 2 poles ),\\ BW &= 1.05f_{3dB} ≈ \frac{1}{6RC} &( 3 poles ),\\ BW &= 1.025f_{3dB} ≈ \frac{1}{6.1RC} &(4 poles ). \end{align*} \]

Для измерения в ограниченной полосе в окрестности некоторой центральной частоты можно поставить два RC фильтра и использовать указанную на рис. 8.97 формулу. Если нужна точная частотная характеристика, то можно взять фильтры Баттерворта более высокого порядка, а эквивалентную шумовую полосу узнать из табл. 8.4 ( стр. 564 ).

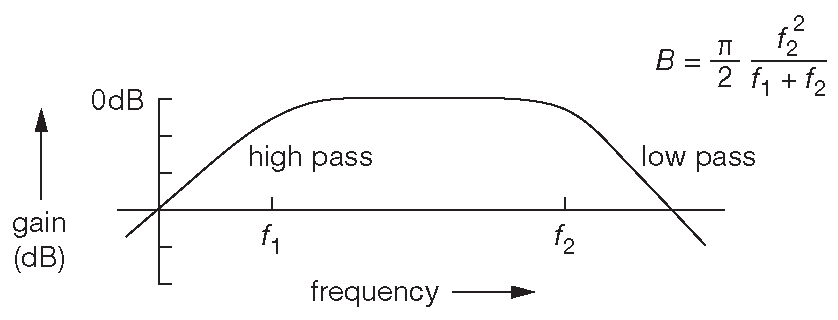
Рис.8.97 Эквивалентная шумовая полоса идеального фильтра, соответствующего полосовому RC фильтру с частотами среза ВЧ и НЧ секций $ f_1$ и $ f_2 $ соответственно. Усиление на центральной частоте в случае $ f_c=f_1=f_2$ составляет -6 dB

==562

RLC фильтр

Ещё один путь - использование в качестве полосового фильтра RLC цепи. Такое решение лучше, чем две последовательных ВЧ и НЧ RC секции, если надо проводить измерения в узкой по сравнению с центральной частотой полосе ( т.е. с высокой добротностью ). На рис. 8.98 показаны параллельная и последовательная RLC цепи и уравнения их частотных характеристик. В обоих случаях резонансная частота определяется формулой $ f_0=1/( 2π\sqrt{LC} ) $ . Такой полосовой фильтр можно включить в качестве коллекторной ( или стоковой ) нагрузки и использовать приведённую формулу. Либо, если вспомнить рис. 1.107 , можно организовать схему в соответствии с рис. 8.99 . При расчёте следует использовать формулу для параллельной RLC цепи, учитывая, что $R=R_1∥R_2$ .

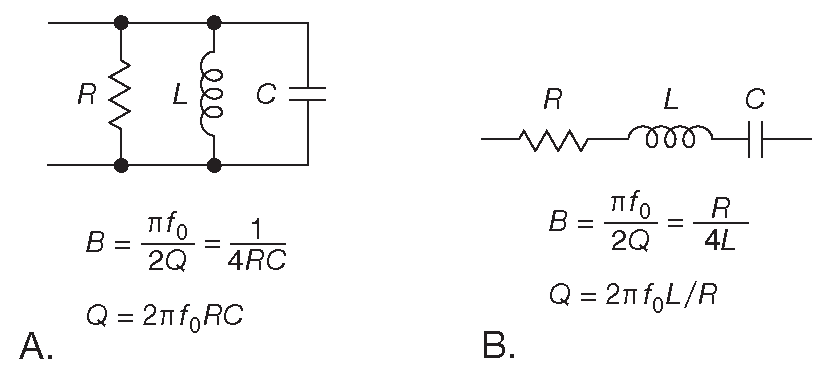
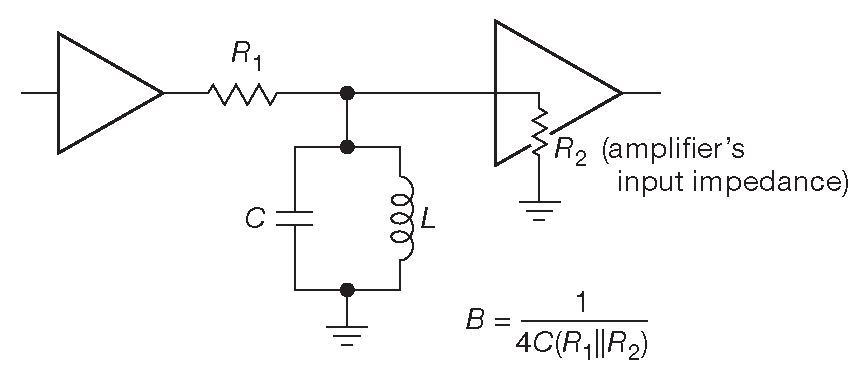
Рис.8.98 Эквивалентная шумовая полоса идеального фильтра, соответствующего полосовому RLC фильтру. Для параллельного включения (A) источником выступает токовый сигнал, а на выходе напряжение на клеммах; для последовательного включения (B) на входе - напряжение, прикладываемое к концам цепи, а на выходе - текущий через неё ток
Рис.8.99 Межкаскадный полосовой RLC фильтр

Усреднение

Как говорилось в §8.1.5 , ещё одним способом низкочастотной фильтрации медленных сигналов ( постоянное напряжение с добавкой белого шума ) является его усреднение по некоторому интервалу T . Это то же самое, что делают интегрирующие АЦП ( например, цифровой вольтметр, см. §13.8.3 ). В этом случае эквивалентная полоса шума ¹²⁵ равна BW=1/(2T) . Таким образом, продолжительность усреднения 1 секунда вмещает полосу шума 0.5 Hz . Это простой «фильтр» нижних частот, но его АЧХ ещё более пологая, чем даже у одной секции RC ( у RC характеристика падает со скоростью 6 dB/octave , а у фильтра с усреднением времени 3 dB/octave ).

Цифровые фильтры

Цифровая обработка сигналов - эффективный метод создания очень хорошо изученных функций фильтрации, характеристиками которых очень удобно управлять, меняя значения коэффициентов. Некоторые подробности см. §6.3.7 .

Перенос частоты

Предположим, что есть задача измерить шумовое напряжение в узкой полосе ( например, 10 Hz ) вокруг достаточно высокой центральной частоты $ f_{in}$ , которая может составлять десятки и сотни килогерц или даже мегагерц. С такими исходными параметрами добротность Q=$ f_{in}/Δ f$ получается очень высокой. Пусть Q=1000 . Фильтр с такой добротностью сделать довольно трудно, но зато есть один способ провести измерения, не проявляя чрезмерный героизм в фильтростроении.

Приём заключается в сдвиге ( переносе ) интересующей полосы вниз в область низких частот, где делать узкополосный фильтр не в пример проще. Такая техника носит название « техникой смешивания сигналов» или « гетеродинной » и является основой большинства систем радиосвязи. Разобраться в теме проще, если считать, что на входе одна частота $ f_{in}$ . На рис. 8.100 приведена базовая схема. Напряжение входного сигнала ( с частотой $ f_{in}$ ) умножается на синусоидальное напряжение с опорного генератора « LO » ( с частотой $ f_{lo}$ ) . В результате получаются два дополнительных синусоидальных сигнала с частотами $ f_{in}±f_{lo}$ ¹²⁶. Выход умножителя, называемого «смесителем», фильтруется, чтобы выделить только одну из смешанных частот. Смеситель может быть как активным ( «четырёхквадрантный умножитель» ), так и, если речь идёт о высоких частотах, пассивной схемой на диодах с трансформаторной связью, называемым «балансным смесителем».

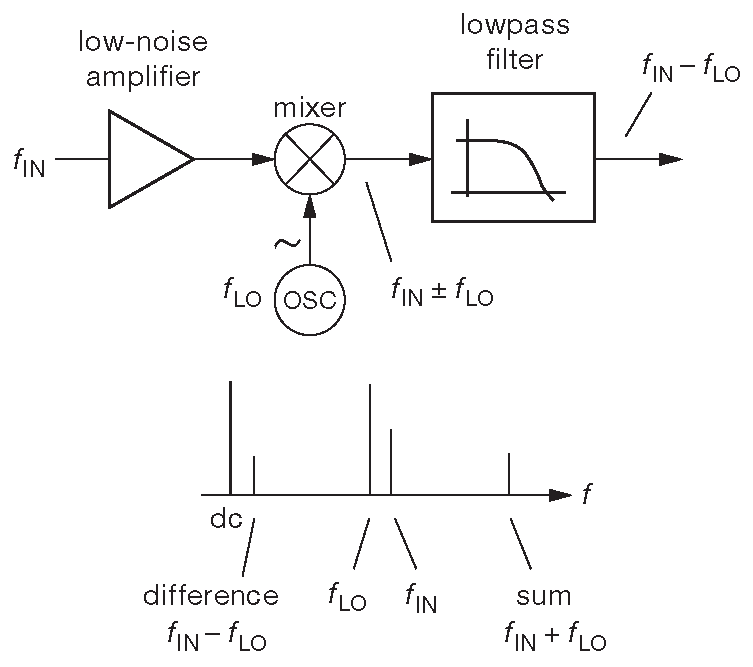
Рис.8.100 Сдвиг частоты в гетеродине: умножитель создаёт сумму и разность частот, но через ФНЧ проходит только разностная составляющая

==563

В связных устройствах может быть несколько ступеней переноса частот, каждая со своей «промежуточной частотой», своими усилителями и своими фильтрами ¹²⁷. В случае простого измерения шума может быть разумно проводить перенос сразу в рабочую полосу, выставив у «LO» ту частоту, на которой предполагается мерить узкополосный шум. Точно такая же схема используется при синхронном детектировании, см. §8.14 и §13.13.6.D . Коммерческие синхронные усилители позволяют проводить узкополосные измерения шума на любой частоте из их рабочего диапазона, который для типовых синхронных усилителей ограничивается 100 kHz , а для отдельных приборов ( SR844 ) достигает 200 MHz .

8.13.2 Расчёт интегрального шума

Начнём с простого ФНЧ из одной RC секции. Из соотношений для эквивалентной полосы идеального фильтра ( см. [8.55] ) после фильтрации белого шума с плотностью $e_n$ получаем интегральное напряжение шума с амплитудой, равной квадратному корню из следующего выражения: \[ v^2_n=e^2_nBW=e^q_n\frac{π}{2}f_{3dB} \qquad \mathrm{V^2(rms)} \qquad [8.56]. \]

Аналогичные действия нужны для расчёта тока.

Ситуация усложняется, если плотность шума $e_n$ зависит от частоты, как это происходит с шумом вида 1/$ f $ ( розовым ). Теперь, чтобы выяснить спектральную характеристику, плотность шума $e^2_n( f$ ) с поправкой на спектральные параметры фильтра надо интегрировать по частоте. В общем случае используется полосовой фильтр с нижней и верхней частотой среза ( назовём их $ f_1$ и $ f_2 $ ) . Тогда идеальный полосовой фильтр будет иметь единичный отклик в промежутке между $ f_1$ и $ f_2 $ и шумовую полосу BW =$ f_2-f_1$ .

Аналоговыми методами добиться вертикального наклона характеристики на частоте среза невозможно, но есть упоминавшийся ранее простой способ, состоящий в использовании двух последовательных RC фильтров с частотами «-3dB», равными $ f_1$ и $ f_2 $ . Это удобная возможность продемонстрировать свои профессиональные качества, черкнув приличествующий случаю интеграл и уточнив шумовое напряжение для «стандартных» видов шума ( белого, 1/$ f $ или даже 1/$ f^2$ ). Но в жизни удобнее использовать возможности программы Wolfram Mathematica. Табл. 8.4 на следующей странице сделал коллега по работе ¹²⁸. В ней собраны данные по трём цветам шума и четырём типам полосовых фильтров: идеальному, простому RC ( первого порядка, состоящего из двух последовательных секций ), Баттерворта 2-го порядка и Баттерворта m-ного порядка.

Приведённые в таблице выражения дают квадрат интегрированного по частоте шумового напряжения $v^2_n$ для известной плотности шума $e_n$ в полосе, заданной граничными частотами «-3dB» $ f_1$ и $ f_2 $ ( рис. 8.101 ). Для среднеквадратического напряжения надо взять квадратный корень из предыдущего результата: $ V_{n(rms)}=\sqrt{v_n^2}$ . Для розового ( мощность 1/$ f $ ) и красного ( мощность 1/$ f^2$ ) шума плотность напряжения $e_n$ есть функция от частоты. В качестве общего масштабирующего коэффициента для формул взят квадрат плотности шума на верхней границе $e^2_n( f_2 ) $ , т.е. при $ f=f_2$ , обозначенный в таблице $e^2_{n2}$ и имеющий размерность V²/Hz .

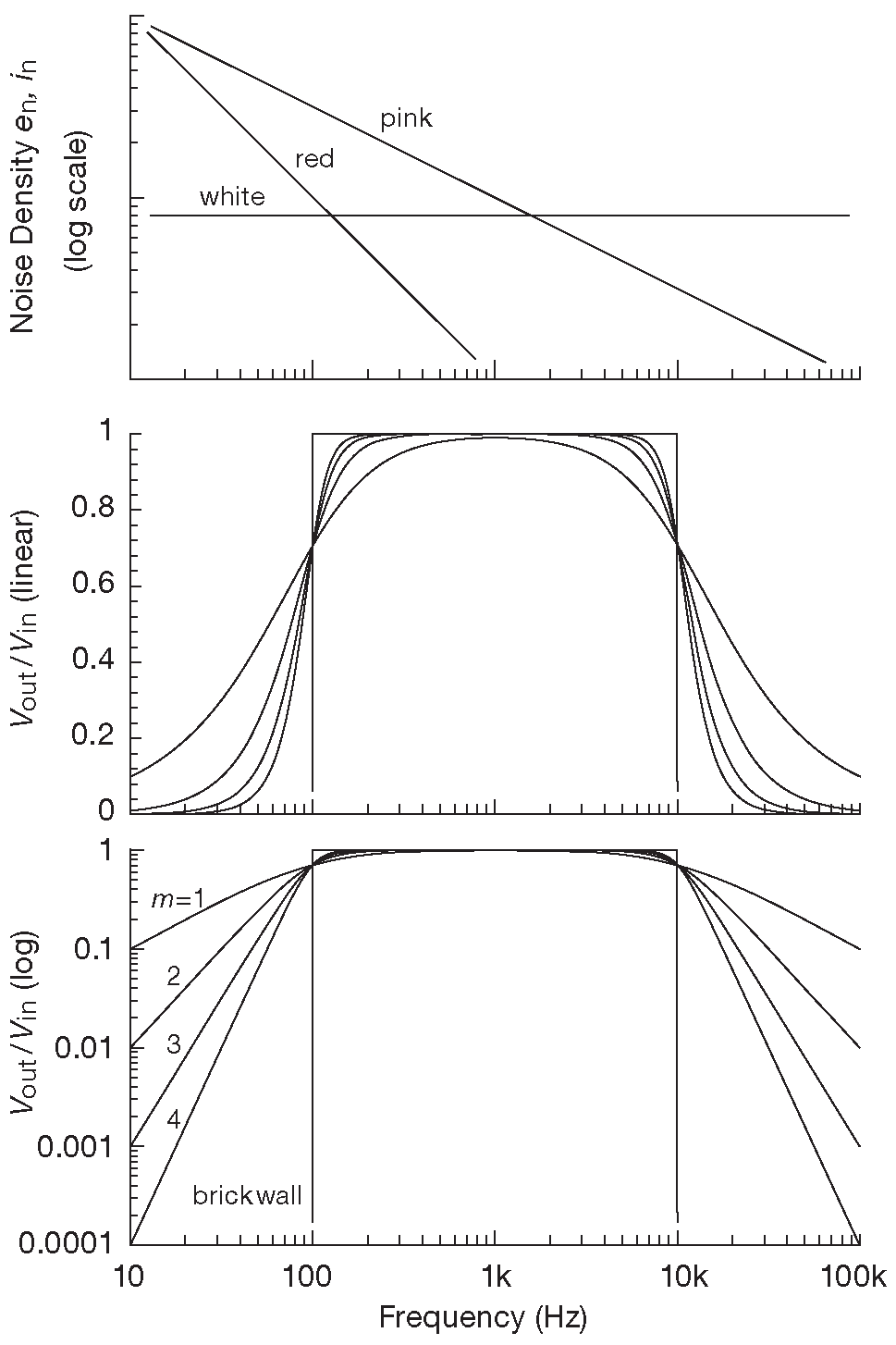
Рис.8.101 Контуры спектров трёх классических видов шума и характеристики полосовых фильтров, используемых для измерения интегрального шумового напряжения и тока

Отметим, что для белого шума допускается брать значение нижней границы $ f_1$=0 . В итоге получается шумовое напряжение для ФНЧ в полосе от постоянного тока до $ f_2 $ , а формула принимает вид, приведённый на стр. 561 . Для розового и красного шума так делать нельзя, потому что вблизи нуля интеграл расходится, приводя к появлению нуля в знаменателе в ходе вычисления логарифма ( для розового ) или в самом результате ( для красного ). Именно поэтому шум вида 1/$ f $ измеряется в полосе 0.1—10 Hz , см. рис. 8.102 и 8.103 .

Формулы для шумового тока выглядят точно так же, нужно только заменить все вхождения $e_n$ на $i_n$ и получить в результате $I_n(rms)$ .

8.13.2.A Верхняя граница важнее

Чтобы подсчитать интегральное шумовое напряжение в некоторой полосе требуется проинтегрировать квадрат плотности шума ($e^2_n$) по частоте, учитывая АЧХ фильтра в полосе пропускания: $\mathbf{H( f)}≡ V_{out}/V_{in}$ , фаза не важна. Итого: \[ v^2_n=\int^{f_2}_{f_1}e^2_n\mathbf{H^2( f)}df \qquad \mathrm{V^2(rms)} \qquad [8.57]. \]

Теперь надо взять квадратный корень из результата $ V_n(rms)=\sqrt{v^2_n}$ .

==564

Таким образом, глядя на АЧХ полосового фильтра в логарифмических координатах, подобную приведённой на рис. 8.101 , в первый момент можно подумать, что нужен фильтр с крутыми срезами и на низкочастотной и на высокочастотной границах. Но ( сюрприз! ) вклад верхнего среза фильтра в интеграл $v^2_n$ отличается от вклада нижнего, как можно видеть на рис. 8.102 , где построена зависимость $e^2_n\mathbf{H^2( f)} $ для белого шума ( $e_n$=1 ) для полосы с соотношением частот 100:1 в линейных координатах ( чтобы показать, как это выглядит в реальности ). Интеграл - площадь под графиком - потихоньку накапливает массу нежелательных компонент спектра, просачивающихся через единственную RC секцию на высокочастотном конце, но соблюдает бОльшую дисциплину при более высоких порядках фильтра. А на низкочастотной границе - срез достаточно резкий для любой цепи заграждения. Такая же картина наблюдается и при меньшей ширине полосы для соотношения частот 10:1 ( рис. 8.103 ).

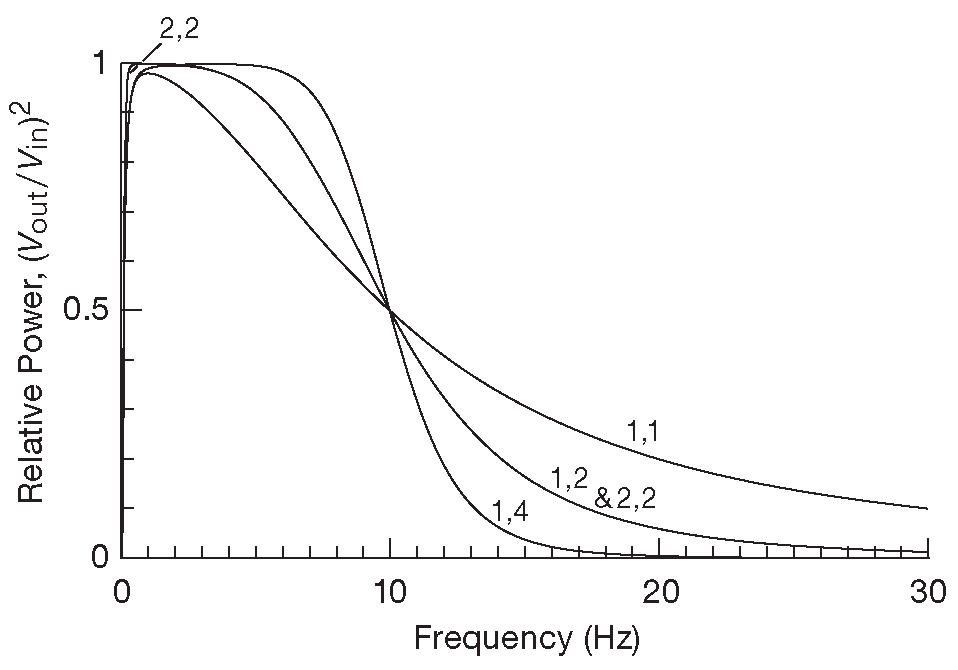
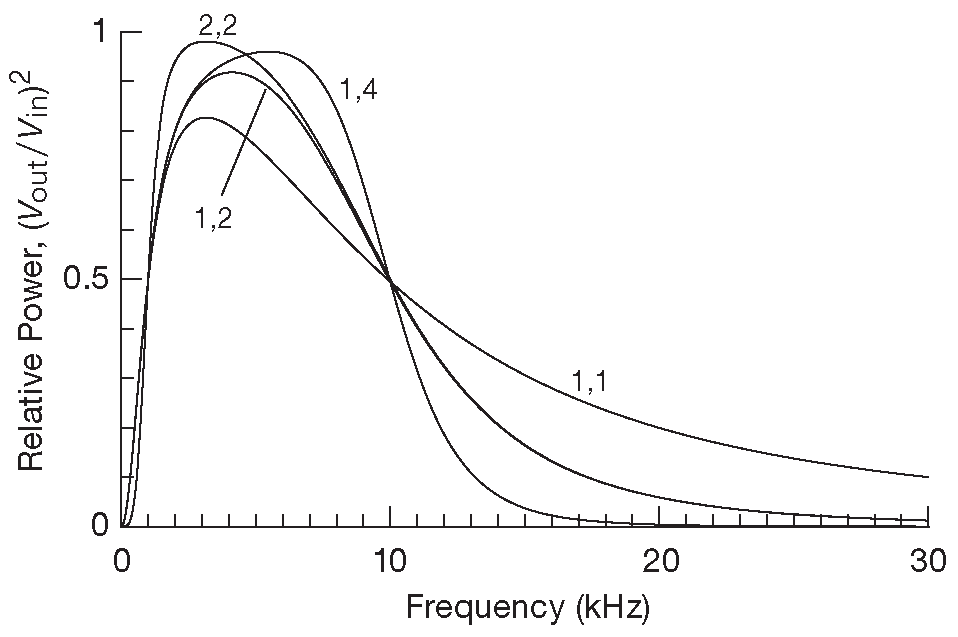
Рис.8.102 Спектр мощности белого шума в полосе 0.1—10 Hz . Порядок фильтров указан возле графика. Цифры «1,2» означают RC ФВЧ первого порядка для $ f_1$ ( «нижняя» граница ) и ФНЧ Баттерворта второго порядка для $ f_2 $ ( «верхняя» граница )
Рис.8.103 Спектр мощности белого шума, пропущенного через фильтр Баттерворта с полосой 1...10 kHz . Порядок фильтра указан в формате «нижний, верхний»

Здесь показана ситуация с белым шумом, имеющим одинаковую спектральную плотность по всем частотам. Но, даже если плотность шума возрастает на низких частотах ( например, для розового шума $e^2_n∝$ 1/$ f $ ) , общая картина меняется незначительно: компонента $\mathbf{H^2}$ , которая пропорциональна $ f^2$ , при интегрировании по низким частотам компенсирует некоторый подъём плотности шума.

8.13.3 «Низкочастотный» шум операционных усилителей и асимметричные фильтры

Из-за того, что «высокочастотная граница важнее», паспортные параметры низкочастотного шума многих ОУ снимаются с асимметричными фильтрами. Чаще всего это одна RC секция ФВЧ на 0.1 Hz и две ( и более ) секции ФНЧ на 10 Hz . Ниже приводятся формулы для эквивалентной полосы шума для случая простого RC ФВЧ первого порядка на $ f_1$ и ФНЧ Баттерворта 2-го порядка на $ f_2 $ . Как и раньше, для розового и красного шума в качестве множителя $e_{n2}$ берётся плотность шума на верхней границе $ f_2 $ , т.е. $e_{n2}≡ e_n( f_2 ):$ \[ \begin{align*} v_n^2 &= e_n^2\frac{π}{4}\frac{\sqrt{2}f_1^2f_2^3-2f_1f_2^4+\sqrt{2}f_2^5}{f_1^4+f_2^4} \qquad &\text{(white )}, \qquad [8.58a] \\ v_n^2 &= e_{n2}^2\frac{πf_1^2f_2^3+4f_2^5\ln( f_2/f_1 )}{4( f_1^4+f_2^4 )} \qquad &\text{( pink )}, \qquad [8.58b]\\ v_n^2 &= e_{n2}^2\frac{π}{4}\frac{\sqrt{2}f_1^3f_2^3-\sqrt{2}f_1f_2^5+2f_2^6}{f_1^5+f_1f_2^4} \qquad &\text{( red )}. \qquad [8.58c] \end{align*} \]

Паспортные данные по низкочастотному шуму ОУ приводятся обычно для полосы 0.1—10 Hz , но ассиметричный фильтр используется только в половине случаев. Что интересно, производители любят приводить амплитудное значение ( а не среднеквадратическое ) полученное по 10-секундной осциллограмме ( аналогичной нижнему графику на рис. 8.4 ). Эмпирическое правило перевода в RMS: $v_n(rms)≈ v_n(pp)$ /6 .

8.13.3.A Напряжение низкочастотного шума операционных усилителей

Современные операционные усилители ( исключая ОУ с автоподстройкой нуля ) демонстрируют сходную форму графика плотности шума: плоский при высоких частотах ( назовём его $e_{nH}$ ) , он начинает возрастать приблизительно как $e_n∝$ 1/$\sqrt{f}$ ( розовый шум ) на частотах, лежащих ниже характеристической точки перегиба $ f_c$ графика 1/$ f $ . Если $ f_c$ и $e_{nH}$ известны, то можно использовать формулы из табл. 8.4 для расчёта интегрального шума для любого соотношения частот $ f_1$ и $ f_2 $ .

Табл. 8.4 Уравнения для вычисления интегральных значений шума ( Noise integrals®)

Шумовые интегралы
1-полюсный RC	$e_n^2\frac{π}{2}\frac{f_2^2}{f_1+f_2}$	$e_{n2}^2\frac{f_2^3}{f_2^2-f_1^2}\ln\frac{f_2}{f_1}$	$e_{n2}^2\frac{π}{2}\frac{f_2^3}{f_1( f_1+f_2 )}$
Тип фильтра	«Цвет» шума
	Белый	Розовый	Красный
	$e_n=const$	$e_n∼1/\sqrt{f}$	$e_n∼1/f$
идеальный	$e_n^2( f_2-f_1$ )	$e_{n2}^2f_2\ln\frac{f_2}{f_1}$	$e_{n2}^2\frac{f_2}{f_1}( f_2-f_1$ )
2-полюсный Баттерворта	$e_n^2\frac{π}{2\sqrt{2}}\frac{f_2^4}{( f_1+f_2 )( f_1^2+f_2^2 )}$	$e_{n2}^2\frac{f_2^5}{f_2^4-f_1^4}\ln\frac{f_2}{f_1}$	$e_{n2}^2\frac{π}{2\sqrt{2}}\frac{f_2^5}{f_1( f_1+f_2 )( f_1^2+f_2^2 )}$
m-полюсный Баттерворта	$e_n^2\frac{π/2m}{\sin(π/2m)}\frac{f_2-f_1}{1-( f_1/f_2 )^{2m}}$	$e_{n2}^2\frac{f_2}{1-( f_1/f_2 )^{2m}}\ln\frac{f_2}{f_1}$	$e_{n2}^2\frac{π/2m}{\sin(π/2m)}\frac{f_2-f_1}{1-( f_1/f_2 )^{2m}}$

Примечание:
интегралы дают квадрат напряжения шума заданного «цвета» $v_n^2$ в полосе от $ f_1$ до $ f_2 $ , ограниченной фильтром указанного типа. Плотность напряжения шума $e_{n2}$ - значение плотности $e_2$ при $ f_1=f_2$

==565

Имеются три возможных варианта:

интересующая полоса целиком лежит в области белого шума, т.е. $ f_1 >f_c;$
полоса целиком лежит в области розового шума, т.е. $ f_2 <f_c;$ и
полоса накрывает точку перегиба $ f_1 <f_c <f_2$ .

Для первых двух случаев следует использовать формулы из табл. 8.4 , соответствующие характеристикам используемого фильтра. Для случая (c) нужно раздельно посчитать вклад в $v_n^2$ белого и розового шума по всей полосе от $ f_1$ до $ f_2 $ и сложить результаты. В случае идеального полосового фильтра в итоге будет следующее выражение: \[ v_n^2=e_{nH}^2\left( f_2-f_1+f_c \ln\frac{f_2}{f_1}\right ) \qquad \mathrm{V^2(rms)} \qquad [8.59]. \]

Именно так были получены кривые интегрального шума на рис. 5.54 ( §5.11.1 ). Они считались по рис. 5.37 ( §5.10.6 ) ( паспортные данные о плотности шума в графическом виде ) и рис. 8.63 ( компиляция данных графиков с рис. 8.60 и 8.61 ) ¹²⁹. На рис. 8.104 показан пример нахождения интегрального шумового напряжения $v_n$ , как функции верхней граничной частоты для графика $e_n$ из паспортных данных на AD8671 ( частота перегиба 1/$ f $ равна 5 Hz ). В качестве нижней границы $ f_1$ следует брать какую-либо ненулевую величину.

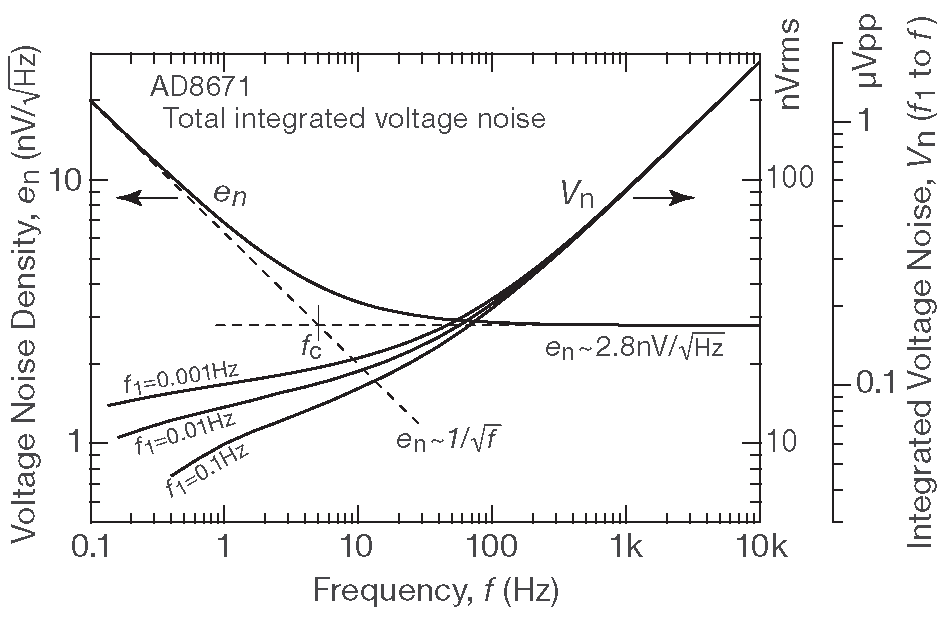
Рис.8.104 Плотность шума $e_n$ этого ОУ имеет характеристическую частоту перегиба графика $ f_c$ , равную 5 Hz . Интегрирование мощности шума ( $∼e_n^2$ ) от нижней границы ( $ f_1$ ) до верхней ( $ f_2 $ ) даёт квадрат интегрального шумового напряжения $v_n^2$ . Именно по этим данным построены кривые $v_n$ . Если $ f_1$ приравнять к нулю, интеграл расходится

==566

8.13.4 Нахождение частоты перегиба графика 1/f

На графике зависимости плотности шума от частоты несложно проследить точку пересечения двух его участков - $ f_c$ , но было бы полезно находить её по паре табличных значений, когда графика нет ( в паспортных данных часто указывается значение $e_n$ для 10 Hz и 1 kHz ). Кроме того, встречаются люди, которым просто приятно увидеть в книге формулу, другую. Графическое пояснение техники можно найти на рис. 8.105 , а вот и сама формула: \[ f_c=\frac{e_{nL}^2-e_{nH}^2}{e_{nH}^2}f_L=\left(\frac{e_{nL}^2}{e_{nH}^2}-1\right )f_L \qquad \mathrm{Hz}, \qquad [8.60] \]

где $e_{nL}$ - плотность шума на некоторой частоте $ f_L$ , которая ниже частоты перегиба $ f_c$ , а $e_{nH}$ - плотность шума сильно выше неё.

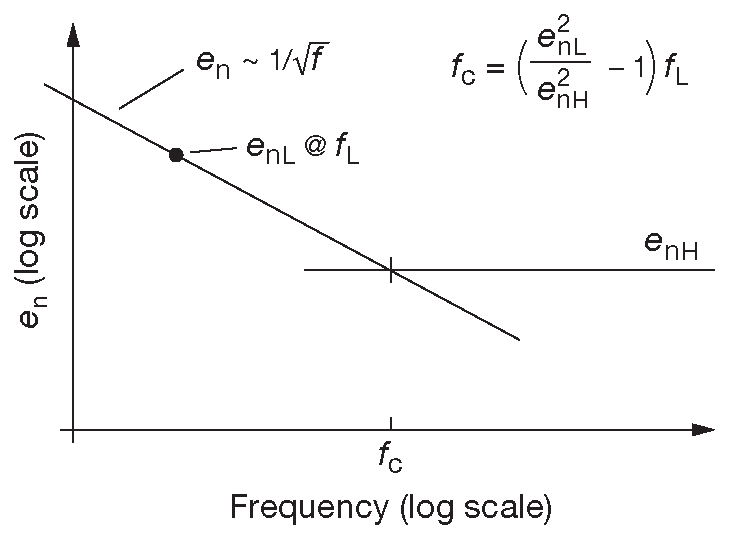
Рис.8.105 Для паспортных данных плотности шума ( плоская на высоких частотах и растёт по закону 1/$ f $ на низких ) можно получить частоту перегиба графика $ f_c$ по величине $e_n$ в двух точках

8.13.4.A Шумовое напряжение по декадам

Источники белого шума ( т.е. $e_n$ - постоянная ), с полосой BW ( скажем, ограниченные идеальным полосовым фильтром BW =$ f_2-f_1$ ) , имеют интегральное напряжение шума $v_n=e_n\sqrt{BW}$ . На основании этого можно заключить, что при рассмотрении шума с полосой шириной одна декада для последовательных декад ( т.е. 0.1—1 Hz, 1—10 Hz, 10—100 Hz и т.д. ), интегральное напряжение шума будет возрастать с коэффициентом $\sqrt{10}$ . Именно поэтому «верхняя граница важнее». В случае розового шума ситуация иная: зависимость вида 1/$ f $ для $e_n^2$ [* падает] компенсирует увеличение частоты [* растёт] , приводя к постоянному напряжению шума, что легко проверить, взглянув на формулу для пропущенного через идеальный фильтр розового шума на стр. 564 . Зависимость хорошо заметна по графикам интегрального шума на рис. 5.54 , 8.62 и 8.63 , где рост вида 1/$ f $ плотности шума обычных ОУ вызывает выравнивание графика интегрального шума в низкочастотной области. Для сравнения, шум усилителей с автоподстройкой нуля остаётся постоянным, поэтому их интегральный шум $e_n$ продолжает уменьшаться со скоростью 10 dB/decade по мере понижения частоты.

Осталось подтвердить эти соображения реальными измерениями. На рис. 8.106 приведены осциллограммы внутриполосного шумового тока биполярного ОУ LT1012. Амплитуда снижается на 10 dB при снижении частоты на декаду, но на низкочастотном краю графика она вновь начинает возрастать. Т.е. скорость роста плотности шумового тока $i_n$ чуть выше, чем 1/$\sqrt{f}$ для розового шума. Спектрограмма шума, снятого с LT1012 на рис. 8.101 показывает, что он и в самом деле «круче», чем розовый. Для ОУ, чей низкочастотный шум повторяет идеальный спектр розового шума, картина иная интегральная амплитуда остаётся почти постоянной от декады к декаде ниже характеристической частоты перегиба 1/$ f $ .

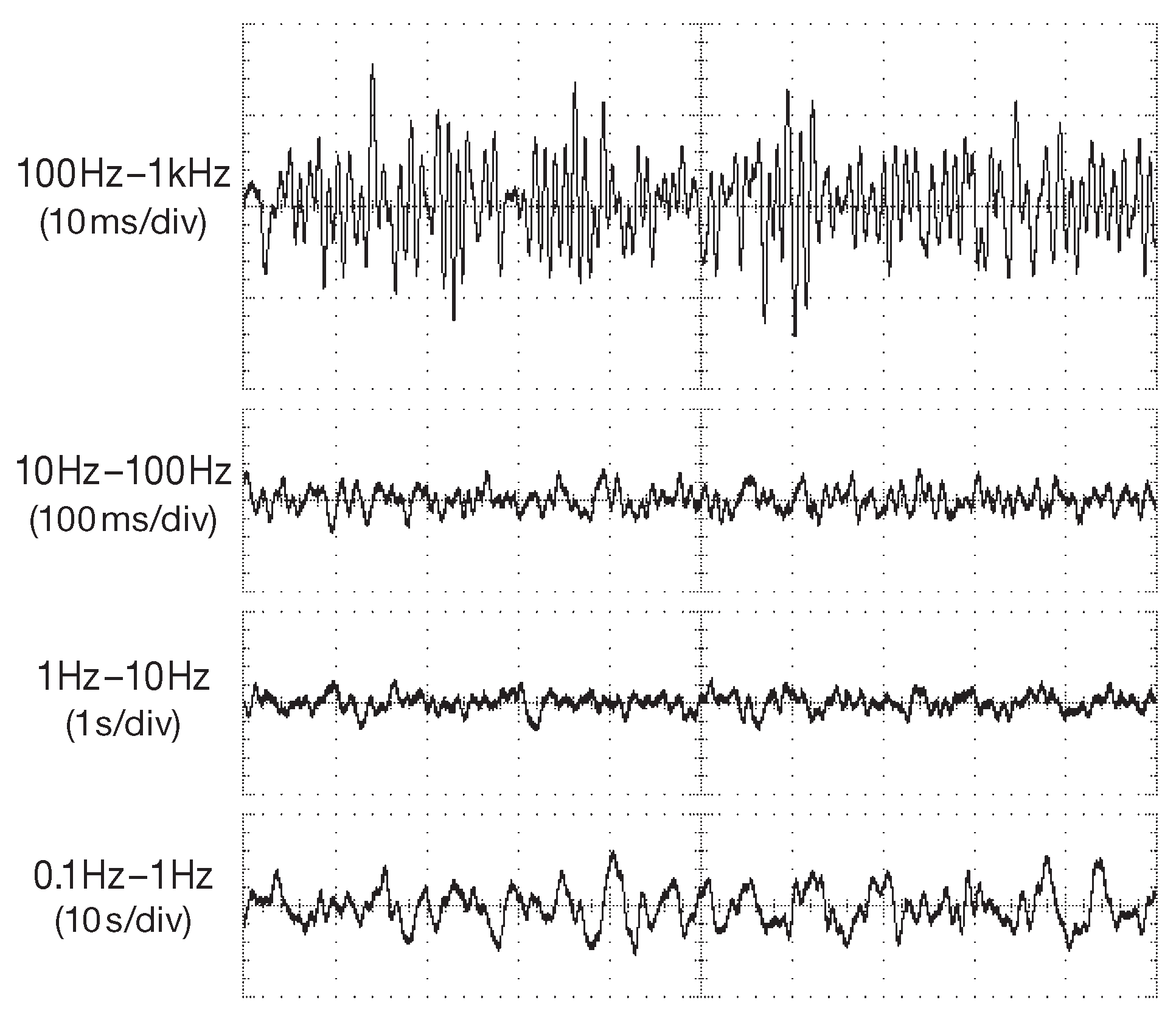
Рис.8.106 Шумовой ток LT1012 для четырёх последовательных декад. Масштаб по вертикали 5 pA/div , масштаб по горизонтали поставлен рядом с каждым графиком

8.13.4.B Неограниченный ужас низкочастотного шума

Очень часто можно слышать, что мощность низкочастотного шума соответствует «закону 1/$ f $», словно речь идёт об уголовном уложении. В первый момент кажется, что тут что-то не так, потому что если спектр мощности 1/$ f $ будет продолжаться бесконечно, то и амплитуда шума будет возрастать бесконечно, и если подождать достаточно долго, то можно увидеть, как мимо проплывает неограниченно возросшее входное напряжение смещения ( или входной ток ). [* Т.е по мере приближения частоты к нулю период растёт бесконечно, и каждую более низкую гармонику приходится ждать всё дольше. При этом разные гармоники складываются, а с учётом аналогового, т.е. непрерывного, характера шума таких гармоник бесконечно много, они всё складываются, складываются, интеграл всё растёт.. И так бесконечно по мере приближения к нулю. Страшно же ]. На самом деле, популярный миф об ужасах низкочастотного шума совершенно не обоснован. Даже если плотность мощности шума со снижением частоты растёт по закону 1/$ f $ , общая мощность шума ( т.е. интеграл его плотности мощности ) расходится только логарифмически в соответствии с уравнением $\int(1/f)df=\ln f$ . В цифрах картина выглядит следующим образом: общая мощность шума со спектром 1/$ f $ между $10^{-6}$Hz ( микрогерцем ) и 10 Hz только в 3.5 раза больше, чем между 0.1 Hz и 10 Hz . Если расширить диапазон вниз ещё на шесть порядков ( до $10^{-12}$Hz ), то соответствующее отношение вырастет только до 6.5 . Иначе говоря, общая мощность шума 1/$ f $ в полосе с нижней границей, соответствующей периоду в 32 тысячи лет ( когда неандертальцы устраивали геноцид мамонтам, а операционных усилителей ещё не существовало ) будет всего в шесть раз больше, чем цифра «низкочастотного шума» для полосы 0.1—10 Hz из паспортных данных. Слишком медленно для катастрофы.

==567

Чтобы понять, как далеко вниз по частоте распространяется соответствие закону 1/$ f $ шума реального усилителя, был измерен спектр токового шума LT1012 вплоть до нижней границы 0.5 mHz ¹³⁰. Результаты представлены на рис. 8.107 . Как отмечалось ранее, данный ОУ необычен тем, что плотность его токового шума $i_n$ на частоте в районе 1 Hz растёт быстрее, чем 1/$\sqrt{Hz}$ ( обычный розовый шум ). Но даже в этом случае он затем возвращается к обычному розовому шуму, а после становится похож на «грязно белый» ( $ f^{-1/4}$ или даже медленнее ).

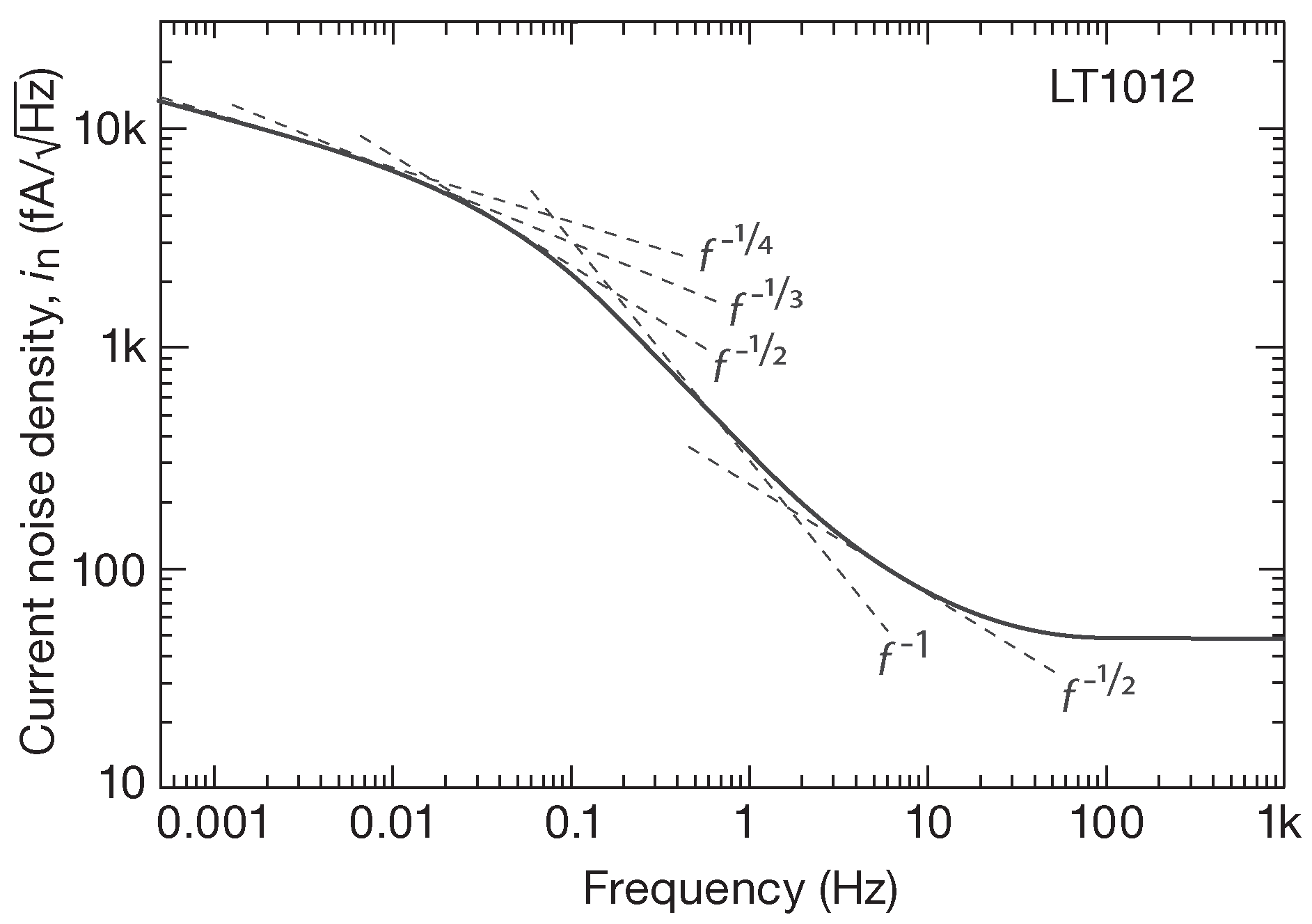
Рис.8.107 Спектр шума LT1012, промеренный до 500 μHz . Для сравнения наложены несколько асимптот

Из всего изложенного можно было бы сделать вывод о нефизической природе шума 1/$ f $ вблизи нуля, но есть и другое объяснение, а именно: у данной модели есть какой-то источник импульсного шума. Это согласуется с «более крутым, чем у розового» спадом в районе 1 Hz ( стоит снова взглянуть на спектры burst-шума на рис. 8.6 ) и якобы неправильным «положе, чем у розового» подъёмом в низкочастотной части рис. 8.107 .

Если последнее утверждение верно, то измерения на ещё более низких частотах ( скажем, 0.00001 Hz ) будут вновь соответствовать наклону 1/$ f $ ( розовому ). Проблема в том, что достижение границы 10 μHz потребует целого дня измерений. Именно в этом причина трудностй получения конкретных цифр. Интересный результат можно найти в отчёте Адама Дэра ( Adam Daire ) об измерениях распределения спектра шума прибора Keithley 6430, проведённых ¹³¹. Прибор имеет высокую чувствительность ( разрешение 0.05 fA ) и показывает символ «1/$ f $» для всех частот вплоть до микрогерц ( соответствующая временная шкала простирается до нескольких недель измерений ). Если учитывать эти факты, то выравнивание графика 8.107 на низких частотах на самом деле является проявлением плато burst-шума. А может, не является: нет такого закона, что низкочастотный шум обязан соответствовать спектру 1/$ f $ , т.е. розового шума.

8.13.5 Измерение напряжения шума

Существует целый класс измерительных инструментов, называемых «анализаторы спектра» или «анализаторы динамического спектра», которые показывают спектр входного сигнала. На одном конце диапазона модели оптимизированные для низкочастотного и звукового спектра до ∼100 kHz или около того и выполняют вычисления с помощью дискретных преобразований Фурье. Типичный пример - Stanford Research Systems SR780/5 и Agilent U8903A. На другом конце – модели для радиочастотного и СВЧ диапазонов, верхняя рабочая граница которых располагается в диапазоне 3...50 GHz . Они используют внутренний генератор качающейся частоты и смеситель ( часто дополненный цифровым блоком быстрых преобразований Фурье ), чтобы отобразить непрерывный ( «панорамный» ) спектр в некотором диапазоне частот из последовательных узкополосных фрагментов. Популярные модели имеют рабочий диапазон 9 kHz...3 GHz , часто со встроенным управляемым генератором, который позволяет исследовать характеристики фильтров и усилителей. Примерами могут служить Agilent E4403 и Rohde & Schwarz FSL3.

==568

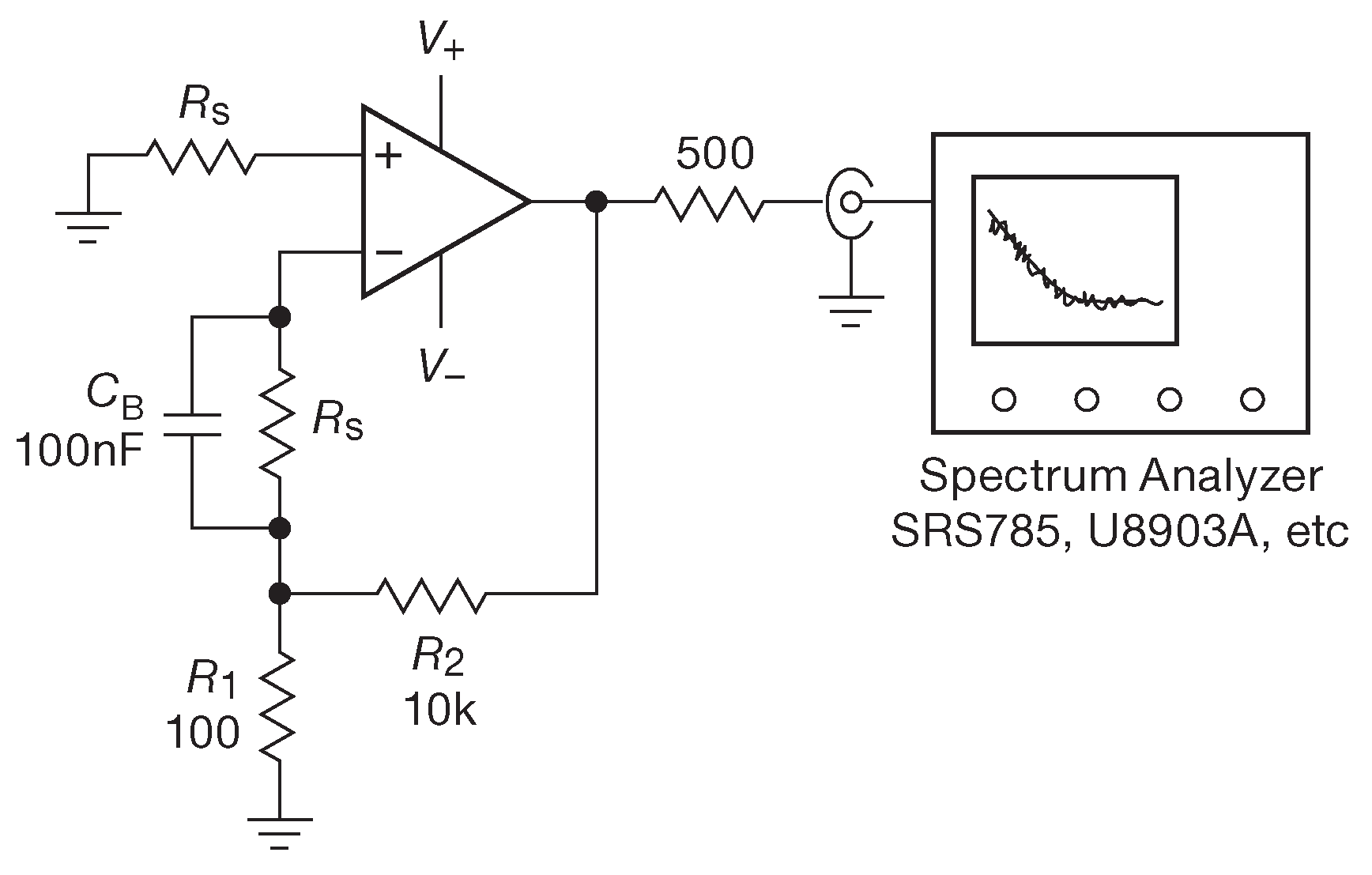
Рис.8.108 Схема измерения спектра шумового напряжения и тока усилителя. Для $e_n$ следует установить $R_S$=0 , для $i_n$ надо подобрать номинал $R_S$ существенно больший, чем шумовое сопротивление усилителя ( $R_n=e_n/i_n$ ) . Для измерений надо использовать экранированную коробку и фильтры на вводах в неё

Анализаторы спектра достаточно универсальные приборы с широкими возможностями настроек усиления, перестройки частоты, масштаба изображения и т.д. Низкочастотные экземпляры для обычных измерений ( например, спектров шума операционных усилителей и источников опорного напряжения ) имеют входной импеданс 1 MΩ . Анализаторы радиочастотного диапазона имеют 50-омный ( или 75-омный для видеосистем ) вход. Чтобы измерить спектр шума операционного усилителя надо включить его по схеме 8.108 с $R_S$=0 . В итоге получится картина, напоминающая рис. 8.109 . Спектры шумового напряжения для нескольких ОУ, измеренные по такой схеме показаны на рис. 8.110 .

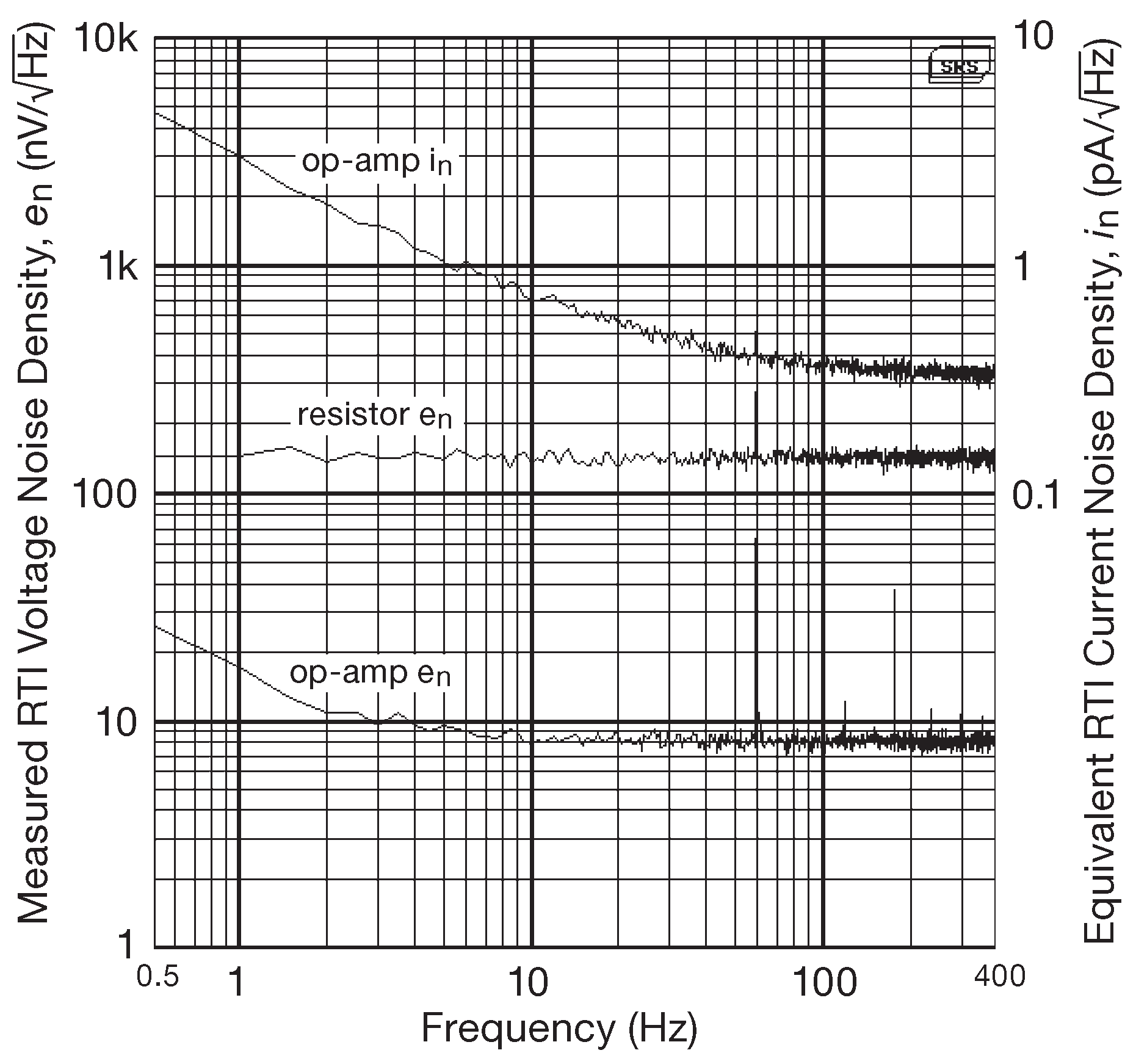
Рис.8.109 Спектры шума тока и напряжения ОУ OPA277, измеренные по схеме 8.108 . В качестве опорного приведён тепловой шум резистора 1 MΩ

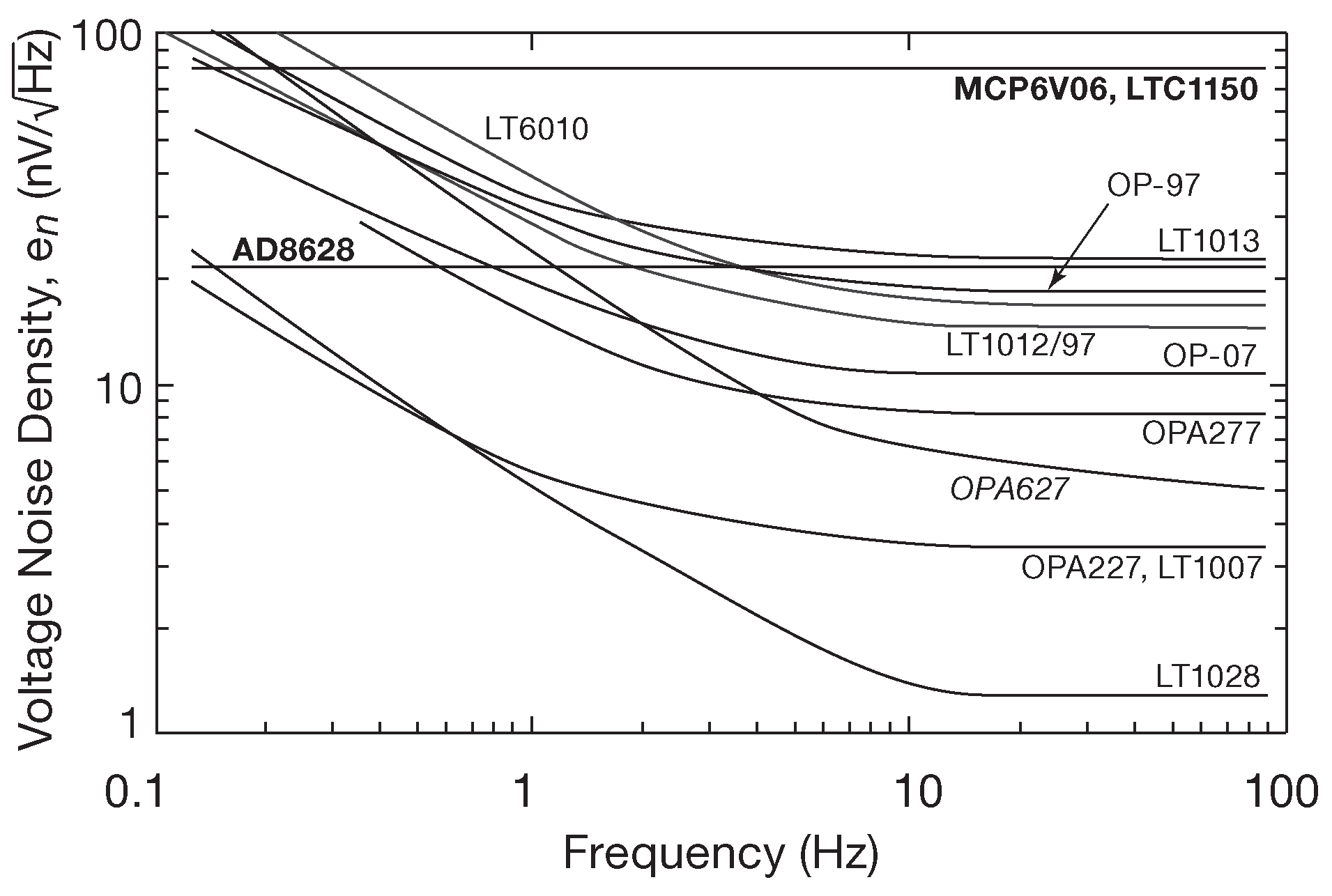
Рис.8.110 Измеренные спектры плотности шумового напряжения для нескольких моделей ОУ. Жирным шрифтом выделены усилители с автоподстройкой нуля, которые обманывают демона «1/$ f $» систематической коррекцией смещения. Курсивом обозначен OPA627 со входом на ПТ, см. также рис. 8.60 и 8.61

Наиболее точный метод измерения интегрального напряжения шума – использование среднеквадратического вольтметра. Такие приборы работают по принципу измерения нагрева при протекании тока произвольной формы ( предварительно подобающим образом усиленного ) или измерения выхода симметричного ограничителя с последующим усреднением результата. Перед использованием таких приборов следует убедиться, что они подходят для работы на нужной частоте: некоторые имеют верхнюю границу измерений, всего несколько килогерц. RMS-вольтметры имеют ещё одну характеристику - форм-фактор - отношение пикового уровня напряжения к среднему, которое прибор допускает без серьёзных потерь точности. Для шума с гауссовым распределением этот коэффициент будет где-то 3...5 .

Вместо RMS можно использовать простой усредняющий вольтметр переменного напряжения. В этом случае показания прибора придётся корректировать. Как оказывается, все усредняющие измерительные приборы ( VOM, DMM и т.д. ) выдают наружу обработанный результат, поэтому то, что видно на индикаторе не усреднённый результат, но значение амплитуды синусоидального сигнала, который имел бы такое же среднеквадратическое напряжение. Например, если мерить напряжение в силовой сети США, то прибор покажет значение, близкое к 117 V . Это замечательно, но если бы измерялся шум с гауссовым распределением, то указанная цифра потребовала бы дополнительной корректировки. Вот правило: чтобы получить RMS напряжение из гауссового шума, требуется умножить значение «RMS» напряжения, считанного с вольтметра переменного тока на 1.13 ( или прибавить 1 dB ).
Предупреждение: такой способ хорошо работает при измерении «чистого» шума ( например, если в качестве источника сигнала выступает резистор ), но не работает, если на входе прибора смесь из синусоидального сигнала и шума.

==569

Есть третий метод, хотя точностью он не блещет: предполагается смотреть сигнал осциллографом. RMS напряжение составляет от 1/6 до 1/8 амплитудного значения ( корректирующий коэффициент зависит от опыта оператора ). Точность так себе, но по крайней мере нет проблем с полосой прибора.

8.13.6 Измерение шумового тока

Простой способ измерения шумового тока - использовать схему 8.108 с большим входным резистором $R_S$ . Его номинал должен быть достаточно велик, чтобы падение напряжения, создаваемое входным шумовым током усилителя, было как минимум сравнимо с шумовым напряжением усилителя ( а лучше, существенно его превышало ): $i_n$$R_S≥e_n$ , т.е. $R_S≥R_n$ .

Это ещё не всё. Необходимо, чтобы произведение $i_nR_S$ было больше плотности напряжения теплового шума: $i_nR_S≥\sqrt{4kTR_S}$ . При таких условиях $R_S$ выглядит как источник токового шума величиной $i_n=\sqrt{4kT/R_S}$ . Таким образом, надо выбирать достаточно большой номинал, чтобы входной шумовой ток усилителя стал заведомо выше. Самый простой способ - запомнить значения напряжения и тока теплового шума для круглых значений сопротивления и масштабировать их пропорционально $\sqrt{R}$ . [* Никак нет. См. предупреждение ниже ] . Итак, тепловой шум резистора 1 MΩ составляет $e_n$=127 nV/$\sqrt{Hz}$ ( выводы разомкнуты ), масштабируется с коэффициентом $\sqrt{R}$ , а токовый шум $i_n$ =127 fA/$\sqrt{Hz}$ ( выводы закорочены ), масштабируется как 1/$\sqrt{R}$ .

[* Масштабный коэффициент $\sqrt{R}$ на самом деле равен результату операции «известный резистор делить на неизвестный и взять корень из отношения». Проверка простая: $\sqrt{R}$ имеет размерность, а коэффициент её иметь не должен; плюс, тепловой шум резистора 1 MΩ составляет $e_n$=127 nV/$\sqrt{Hz}$ ( см. выше ), а тепловой шум резистора $R_S$=100 MΩ равен 12.7 nV/$\sqrt{Hz}$ ( см. ниже ) ].

Спектр входного токового шума для нескольких операционных усилителей ( по большей части биполярных со схемой компенсации входного тока ) показан на рис. 8.111 . Измерения проводились по схеме 8.108 с $R_S$=100 MΩ ( для этого номинала цифры плотности напряжения и тока теплового шума совпадают и составляют 12.7 nV/$\sqrt{Hz}$ и 12.7 fA/$\sqrt{Hz}$ ) . В той же схеме был измерен шум OPA627 с ПТ на входе ( вклад от его шумового напряжения и тока совершенно незначителен ). Две модели с автоподстройкой нуля имеют плоский спектр шума, выделяясь на фоне подъёма 1/$ f $ у обычных ОУ. Но у усилителей с автоподстройкой в спектре есть отвратительные пики на более высоких частотах, вызванные работой переключающих цепей на входе ( для AD8628A переключение происходит на частоте 15 kHz , которая лежит за правой границей рисунка, но зато на рис. 5.52 для MCP6V06 он явлен во всей красе ).

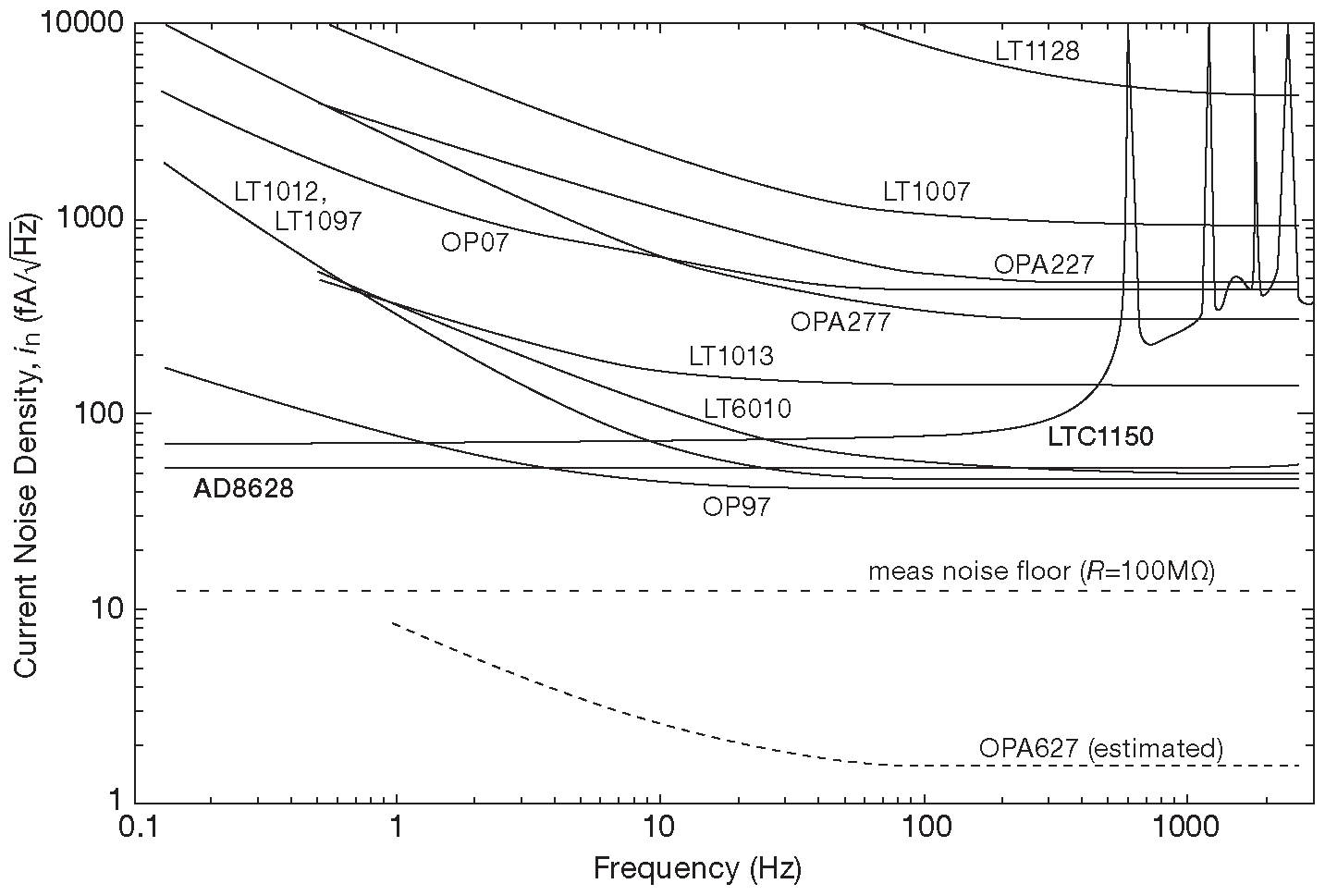
Рис.8.111 Измеренные спектры плотности токового шума для большей части ОУ с рис. 8.110 . Жирным начертанием выделены модели с автоподстройкой нуля, которые обманывают демона «1/$ f $» с помощью постоянной коррекции смещения, но зато имеют шумовые пики, обусловленные тактовым сигналом, на более высоких частотах ( см. увеличенный график на рис. 5.52 ). См. также рис. 8.60 и 8.61

Предупреждение: паспортные значения входного токового шума иногда содержат ошибочные данные. Вероятнее всего, производитель просто не проводил реальных измерений, понадеявшись на результаты расчётов дробового шума по величине постоянной составляющей входного тока. Авторы активно интересовались темой и промеряли входной шум десятков ОУ с автоподстройкой. Результаты собраны в табл. 8.5 на стр. 569 . И вот какая интересная вещь выяснилась! Паспортные данные по напряжению шума правильные, а данные по току у некоторых типов ОУ оказались чересчур оптимистичными ( расхождение порой составляло почти два порядка ). Интереснее всего, что кое-где даже прямо указывалось как были получены цифры, например, у всех трёх моделей LTC справочный параметр $i_n$ сопровождался сноской, гласящей: «токовый шум рассчитывался по формуле $i_n=\sqrt{2qI_B}$ , где $q=1.6×10^{-19}$ кулон». Та же ошибка поразила некоторые ОУ на БТ, а именно те, где применена схема компенсации входного тока. Неправильная цифра входного шума в паспортных данных явно была посчитана для дробового шума, соответствующего «чистому» ( т.е. скомпенсированному ) входному току, а не гораздо большему исходному входному току. Подробности см. ##§X4.10 и §5.10.8 .

Табл. 8.5 Параметры шума ОУ с автоподстройкой нуля Notes: (a) broad spectrum, slight rise at 2.2 kHz and harmonics. (b) output noise dominated by $v_n$ , unable to measure $i_n$ separately. (c) auto-zero at power-up, no corrections thereafter. (d) precision conventional CMOS op-amp, for comparison. (e) at $10 Hz$/$1 kHz$. ( f) no spectral features; peak amplitudes for bandwidths to $1 kHz$/$10 kHz$/100 kHz. ( g ) at 1 Hz. ( s ) spikey waveform, value listed is the peak amplitude. ( t ) typical.

==570

8.13.6.A Некоторые ограничения: полоса, устойчивость, постоянное смещение

Простая схема измерения $i_n$ , когда тестируемый компонент усиливает свой собственный шум ( в виде падения напряжения на входном резисторе ), имеет некоторые недостатки, которые сильно ограничивают возможности по измерению шума в диапазоне fA/$\sqrt{Hz}$ и ниже. Как уже говорилось, при измерении шумового тока приходится использовать резисторы $R_S$ большого номинала, чтобы отстроиться от его теплового шума и $e_n$ усилителя. Скажем, для тока 1 fA/$\sqrt{Hz}$ нужен $R_S$ с номиналом как минимум 10 GΩ ( эквивалентный шум $i_n$ =1.3 fA/$\sqrt{Hz}$ ) . Но теперь надо заботиться о постоянном падении напряжения на нём, вызванном входным током: ток 10 pA сместит вход на 100 mV и вызовет насыщение выхода при усилении G=100 . Кроме того, нужно побеспокоиться об устойчивости, так как достаточно добавить совсем немного ёмкости в цепь обратной связи, чтобы превратить усилитель в генератор. Предотвратить такое развитие событий можно небольшим шунтирующим конденсатором, подключённым к земле, но дополнительная ёмкость сокращает и без того скромную полосу: $R_S$=10 GΩ и шунтирующая ёмкость всего 1 pF сокращают полосу измерения до 16 Hz ! А если на плате имеется тестовая панелька, то для предотвращения низкочастотной генерации ёмкость должна быть ещё больше.

8.13.6.B Увеличение рабочей полосы с помощью усилителя тока

Сухой остаток от предыдущего абзаца состоит в том, что измерить небольшой токовый шум хорошего усилителя не так-то просто. Задачу легче решить, используя аккуратно рассчитанный внешний токовый усилитель ( с низкоомным входом, т.е. виртуальной землёй ), подключённый непосредственно к неинвертирующему входу тестируемой микросхемы в соответствии с рис. 8.112 . Например, токовый предусилитель «модель 1211» фирмы DL instruments ¹³² имеет паспортный токовый шум 1.5 fA/$\sqrt{Hz}$ ( соответствующий резистору обратной связи 10 GΩ , подключённому к суммирующей точке ) и полосу измерения 400 Hz . Он имеет «электрометрическую» конфигурацию ( обратная связь по постоянному току с подключением к суммирующей точке ) и удерживает потенциал входов в пределах 0.2 mV от уровня земли при максимальном входном токе. К другим поставщикам усилителей с малым токовым шумом и токоизмерительных инструментов относятся: Laser Components модель DDPCA-300 с переключаемым усилением от $10\space^4$ до $10\space^{13}$ V/A и токовым шумом на самых чувствительных диапазонах на уровне 0.2 fA/$\sqrt{Hz}$ , Keithley Model 428 с переключаемым усилением от $10\space^3$ до $10\space^{11}$ V/A .

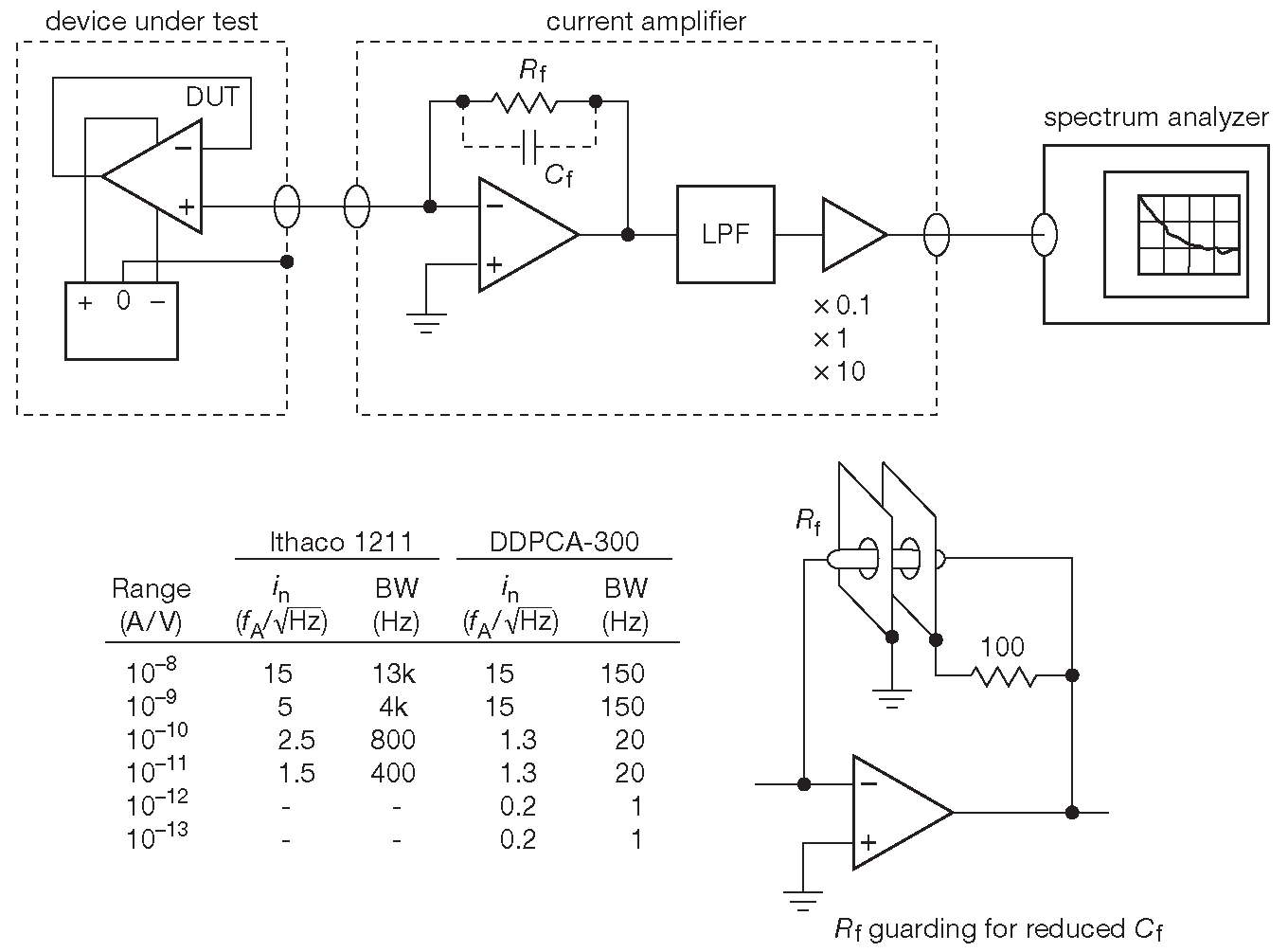
Рис.8.112 Измерение шума ОУ с помощью внешнего чувствительного токового усилителя

==571

8.13.7 Другой путь: создание собственного прибора диапазона fA на корень из Hz

Высококачественные коммерческие усилители тока могут стоить как чугунный мост - речь может идти о суммах 30-40 dB$. Конечно, было бы замечательно разжиться таким прибором, но если всё, что требуется - это измерять слабый шум входного тока операционного усилителя, а монтаж электроники затруднений на вызывает, можно собрать устройство, подобное изображённому на рис. 8.113 . С указанными на схеме номиналами можно мерить шум вплоть до 0.1 fA/$\sqrt{Hz}$ ( или ниже при более высоких номиналах $R_S$ ) при общей цене компонентов всего несколько долларов.

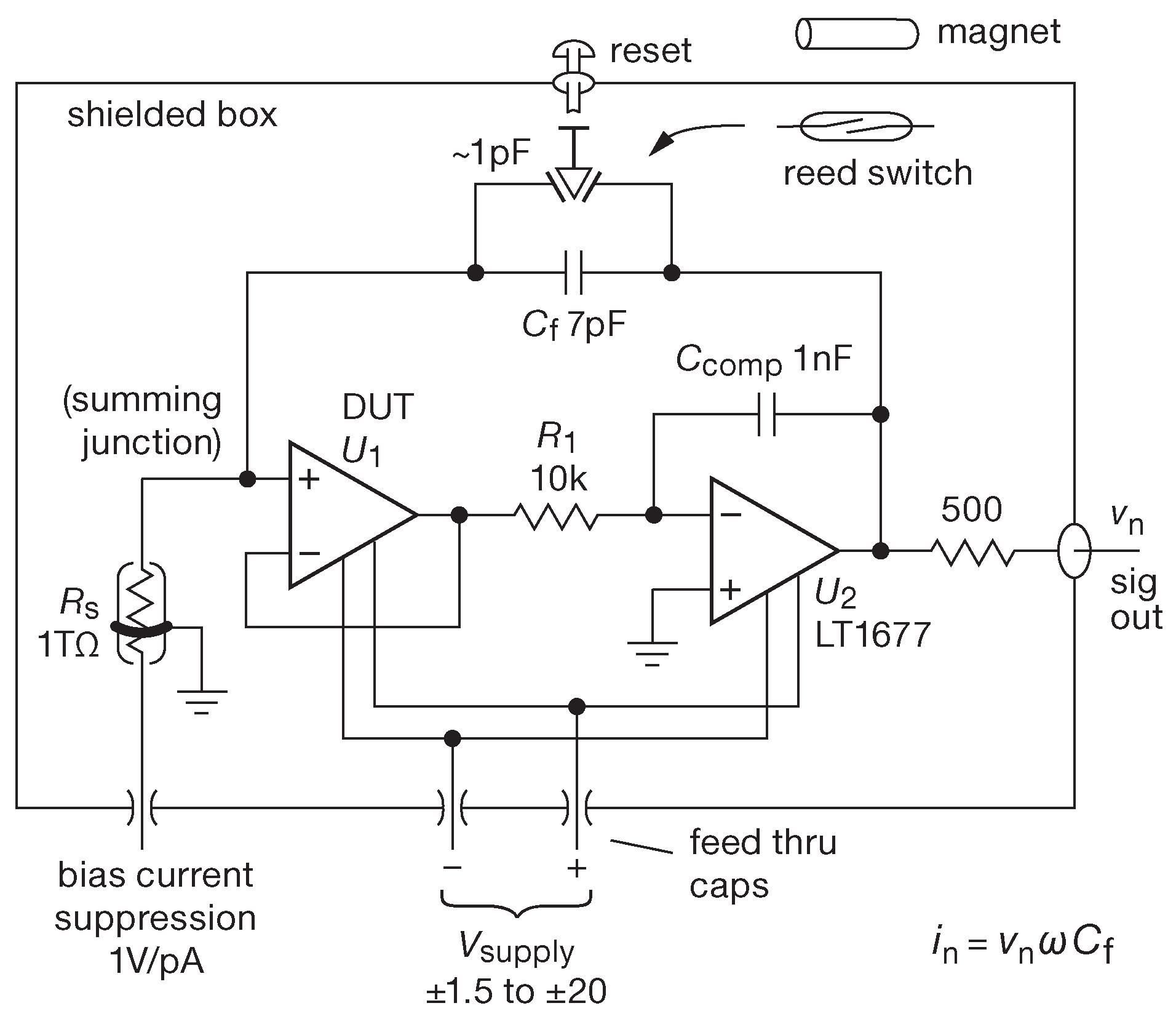
Рис.8.113 Схема для измерения токов до 0.1 fA/$\sqrt{Hz}$ , в полосе до ∼1 kHz с использованием интегратора на композитном усилителе. Понижающий ток резистор ( производства Welwyn ) имеет встроенное защитное кольцо, предотвращающее утечки по внешней поверхности стеклянного корпуса ( это и в самом деле высокоомный резистор: Тераом - это миллион Мегаом! ). Указанное значение $ C_f$ ( 7 pF ) включает ёмкости монтажа и контактной группы, каковая группа, к слову сказать, заставила изрядно помучиться, см. текст

Схема несколько необычная и заслуживает некоторых пояснений. Первой мыслью было совсем избавиться от источника шума в виде резистора обратной связи. Дело в том, что резистор $R$ создаёт тепловой шум с плотностью напряжения $e_n=\sqrt{4kTR}$ и тока $i_n=\sqrt{kT/R}$ , и, чтобы плотность шумового тока была меньше 1 fA/$\sqrt{Hz}$ , номинал резистора должен превышать 16GΩ ( со всеми сопутствующими проблемами в виде полосы измерения, входного смещения и устойчивости ). Поэтому в схеме используется конденсатор обратной связи ¹³³. Схема превращается в интегратор, выполненный в виде композитного усилителя, в котором тестируемый усилитель ( DUT ), включённый повторителем, нагружен усилителем в инвертирующем включении, чья полоса единичного усиления ограничена постоянной времени $R_1C_{comp}\space $ до ∼16 kHz . Более широкая полоса не нужна, а устойчивость схемы увеличивается.

Забудем ненадолго о токе утечки тестируемого усилителя. Интегратор преобразует входной токовый шум в выходное напряжение $v_n=i_n/(ωC_f) $ . Для плоского ( белого ) спектра $i_n$ будет получено напряжение $v_n$ , чей спектр падает по закону 1/$ f $ , а плотность мощности шума - как 1/$ f^2$ ( красный шум ). Конечно, ещё есть напряжение шума $e_n$ обоих ОУ, которое добавится к $v_n$ ( по обычной схеме для независимых источников: как корень из суммы квадратов ). Чем меньше номинал $ C_f$ , тем меньше эффект от обоих $e_n$ , потому что, чем меньше $ C_f$ , тем больше коэффициент передачи ток-напряжение. Ещё один метод учёта действующего токового шума, источником которого является шумовое напряжение $i_n=e_nωC_f$ . Аналогично, измерение токового шума проводится до частоты $ω=i_n/(e_nC_f) $ , выше которой начинает преобладать шумовое напряжение. В качестве $U_2$ выбран LT1677: он хорош сочетанием довольно малого напряжения шума ( 3.2 nV/$\sqrt{Hz}$ ), малого входного тока, широкого диапазона питания ( от ±1.5 до ±20 V ) и RR выходами.

==572

На рис. 8.114 показан снимок спектра шумового напряжения схемы 8.113 с LTC1049 в тестовой панельке. Усилитель точно соответствует закону 1/$ f $ , имея в полосе измерения шум величиной $v_n$=100 fA/$\sqrt{Hz}$ , что согласуется с результатами измерений $i_n$ по схеме 8.108 ( эта цифра указана в табл. 8.5 на стр. 569 ). Никаких намёков на выравнивание шума $e_n$ и $i_n$ на высокочастотном конце нет, что согласуется с величиной выбранной полосы измерения для этого ОУ ( ∼10 kHz ).

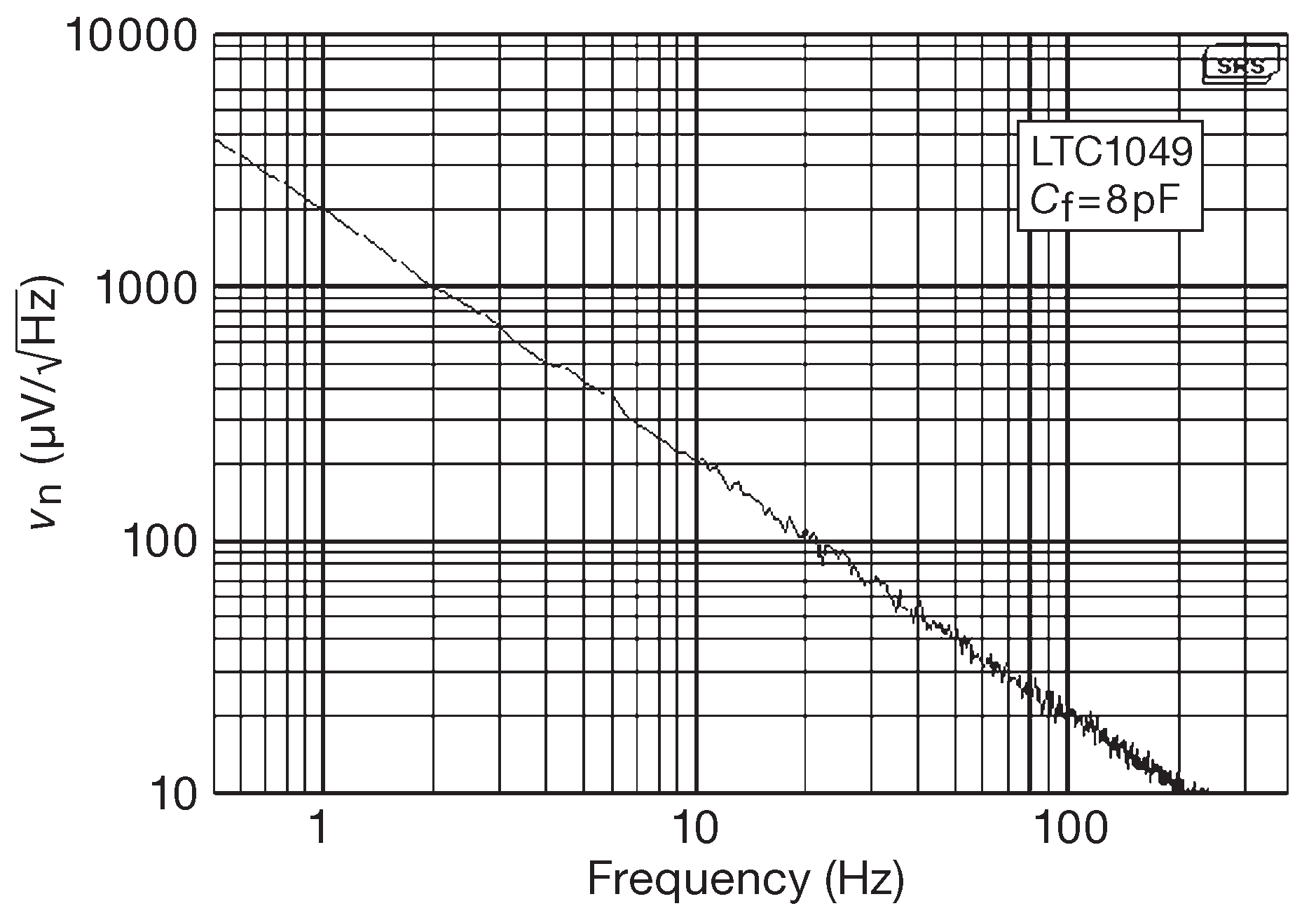
Рис.8.114 Данные измерений для LTC1049 с автоподстройкой нуля в схеме 8.113 . Спектр выходного напряжения интегратора $v_n$ соответствует плоскому спектру токового шума в указанном частотном диапазоне. Величина шума $i_n$ = 100 fA/$\sqrt{Hz}$

После проведения калибровки ( и её проверки измерением AD8628 с автоподстройкой нуля ) схема была использована для измерения параметров ОУ для табл. 8.5 , чей токовый шум может принимать значения вплоть до 1 fA/$\sqrt{Hz}$ . Для таких измерений полосу нужно ограничивать величиной ∼1 kHz , выше которой шумовое напряжение $e_n$ и входная ёмкость ОУ ( в том числе ёмкость монтажа и т.д. ) создают токовый шум «$e_nC$» ( точнее, $e_nωC_{in}$ ) , который начинает забивать собственный токовый шум усилителя.

==573

Кроме того был обмерен LMC6081 с паспортным входным током $I_B$ на уровне 10 fA . Для этой микросхемы $v_n$ соответствовал шуму $i_n$ =0.15 fA/$\sqrt{Hz}$ . Цифра замечательная, но ожидаемая величина дробового шума, посчитанная по входному току должна быть несколько ниже - на уровне 0.06 fA/$\sqrt{Hz}$ . Поэтому теперь в умысле на теракт против безрезисторной чистоты параметров схемы подозревается «понижающий ток резистор» $R_S$ , который давит входной постоянный ток. Чтобы снизить дополнительный токовый шум, здесь используется очень большой номинал: 1 TΩ =$10\space^6$MΩ . Его вклад составляет $i_n=\sqrt{4kT/R_S}$=0.13 fA/$\sqrt{Hz}$ , т.е. в случае LMC6081 измерялся шум ограничительного резистора! Параметры схемы можно улучшить, увеличив номинал $R_S$ до 100 TΩ ( например, взяв резистор Welwyn серии 3810 ) и сократив тем самым шум на порядок. А можно и больше, но придётся защищаться от всех прочих видов паразитных сопротивлений: загрязнений, отпечатков пальцев и т.п., которые также являются сопротивлениями с очень большими номиналами ¹³⁴.

8.13.7.A Занятное осложнение: ключ сброса

Вот короткая история из жизни, повествующая о необычных трудностях, встречающихся на пути к совершенству. Поначалу - сразу после изготовления - устройство работало хорошо, но была одна необычная проблема: при нажатии на кнопку сброса выход послушно сбрасывался в ноль, но после её отпускания скачком возвращался в диапазон от +1.5 до +2.0 V . Что за чудеса? Картина больше всего походила на перенос электростатического заряда за счёт перемещения пластиковых деталей кнопки. Использовался переключатель из модельного ряда Panasonic EVQ2130x..EVQ2150x - маленький, дешёвый, с приятным срабатыванием и практически совершенно свободный от дребезга контактов ( а потому имевшийся в товарных количествах на складе ).

После некоторых размышлений он был заменён на магнитоуправляемый контакт - стеклянную трубку с двумя пластинками, которые притягиваются друг к другу под действием небольшого магнита ( такие устройства часто используются в сторожевых устройствах в качестве датчиков открытия дверей и окон ). Параметры нового переключателя были вполне на уровне: ёмкость в разомкнутом состоянии ∼0.3 pF , а сопротивление изоляции - 1 TΩ , причём в ситуации, когда переключатель стоит на плате внутри алюминиевого корпуса, а магнит находится снаружи, нет никаких путей переноса и накопления статического заряда. Такой способ лучше, чем использование магнитного поля от катушки постоянного тока, как в заводских реле, т.к. отсутствуют магнитные и электрические наводки на чувствительные цепи.

Этот вариант работал гораздо лучше, но по-прежнему не так, как ожидалось: вообразите удивление разработчика, наблюдающего на выходе схемы скачок –50 mV при размыкании контактов. Возникло предположение, что эффект вызывается инжекцией заряда в соседние цепи при изменении магнитного потока в ходе размыкания контактов из магнитного материала. Проверить такое предположение легко: достаточно уменьшить площадь контура, переместив переключатель ближе к операционному усилителю, что и было немедленно проделано. Ступенька на выходе изменила знак ( перепад остался почти такой же по модулю, но теперь в положительном направлении ). Ага! Значит надо вернуться на полшага назад и чуть увеличить контур, чтобы нащупать точку с нулевым перепадом. Но не тут-то было: те же +50 mV !

Чудеса какие-то! В ходе разбирательства возникло предположение, что при первой переделке могли быть поменяны местами два провода. Концы перебросили обратно - вуаля! - перепад изменил знак: опять –50 mV .

Значит в магнитоуправляемом переключателе есть асимметрия и эффект памяти: контакты инжектируют небольшой заряд ( $Q=C_fΔ U$ =0.35 pC ) при размыкании. Чем это может вызываться? Предполагалось, что он порождается различиями в материале контактов ( которые, возможно, намеренно выбираются различными, чтобы избежать слипания из-за возможного эффекта «холодной сварки» ). Старшие товарищи подтверждали эти подозрения и бубнили что-то о «уровнях Ферми», «разнице потенциалов» и «схеме Кельвина», чтобы всё это измерить.

Ладно, можно попробовать переключатель другого типа или иного производителя. Использовавшийся изначально Hamlin MDRR-4 был заменён сначала на Hamlin MDSR-10, затем на Coto RI-01BAA. Эффект и не думал исчезать, менялась лишь амплитуда ( 15 mV и 100 mV соответственно ).

Самое время обратиться в службу технической поддержки. Паспорт на продукцию Hamlin радушно зазывал: «за подробными электрическими характеристиками обращайтесь в компанию Hamlin», что и было сделано. И они сказали, что оба контакта в паре совершенно одинаковые, что они делают какие-то офигильярды таких контактов и берут две штуки наугад из общей кучи. Создавалось впечатление, что дело идёт к углублённому изучению теории уровней Ферми.

Его разъяснили, конечно ¹³⁵! Стекло - чертовски хороший изолятор, и очень легко поместить заряд на поверхности стеклянного корпуса контакта, просто вынимая его из пластиковой упаковки. Официальное название такого явления - «трибоэлектрический эффект». Его часто называют статическим электричеством. Одной из классических демонстрационных пар является стекло и шерсть. При трении стеклянного стержня о кошачью шерсть некоторый заряд остаётся на поверхности стекла ¹³⁶. Он создаёт электрическое поле, которое притягивает заряды противоположного знака при размыкании электрической цепи.

==574

Чтобы решить проблему, магнитоуправляемый контакт был протёрт несколько раз по всей длине куском металлизированной ткани ¹³⁷, заземлённой на одном конце с помощью клипсы, чтобы обеспечить сток накопленного на стекле заряда. И заряд был снят, а скачок напряжения на выходе уменьшился до пренебрежимо низкого уровня ∼2 mV .

Мораль: точные, чувствительные измерения ( на уровне фемтоампер и пикофарад ) могут выявить эффекты столь незначительные, что о них обычно никто не задумывается, но способные серьёзно осложнить жизнь. Тем интереснее самостоятельно доискаться до причин и убить их всех!

8.13.8 Некоторые любопытные факты о шуме

Здесь собрана коллекция интересных и полезных фактов.

Среднее время, за которое шумовые флуктуации в выпрямленном шумовом сигнале снизятся до желаемого уровня при заданной полосе шума, равно \[ τ ≈ \frac{1600}{B\sigma ^2} \qquad \mathrm{seconds,} \qquad [8.61] \] где $τ$ - время, которое требуется, чтобы разброс показаний измерительного прибора на выходе линейного детектора, имеющего на входе шумовой сигнал с полосой BW , снизился до величины ( в процентах ), равной стандартному отклонению $\sigma$ .
Для ограниченного по полосе белого шума ожидаемое число пиков за секунду равно \[ N=\sqrt{\frac{3( f_2^5-f_1^5 )}{5( f_2^3-f_1^3 )}} \qquad \qquad [8.62] \] где $ f_1$ и $ f_2 $ - нижняя и верхняя граничные частоты рабочей полосы. Если $ f_1$=0 , то N=0.77$ f_2;$ для узкополосного шума ($ f_1≈ f_2$ ) , $ N≈ ( f_1+f_2$ )/2 .
Отношение среднеквадратического напряжения к среднему:
- Для шума с гауссовым распределением: $ rms/avg = \sqrt{π/2}$ =1.25 =1.96 dB ,
- Для синусоидального сигнала: $ rms/avg = π/( 2\sqrt{2}$ ) =1.11= 0.91 dB ,
- Для прямоугольного сигнала: $ rms/avg$ =1 =0 dB .
Максимумы с заданной амплитудой в шуме с гауссовым распределением. На рис. 8.115 дано время в долях целого, в течение которого амплитуда шума с гауссовым распределением превышает заданный уровень в единицах среднеквадратической амплитуды.

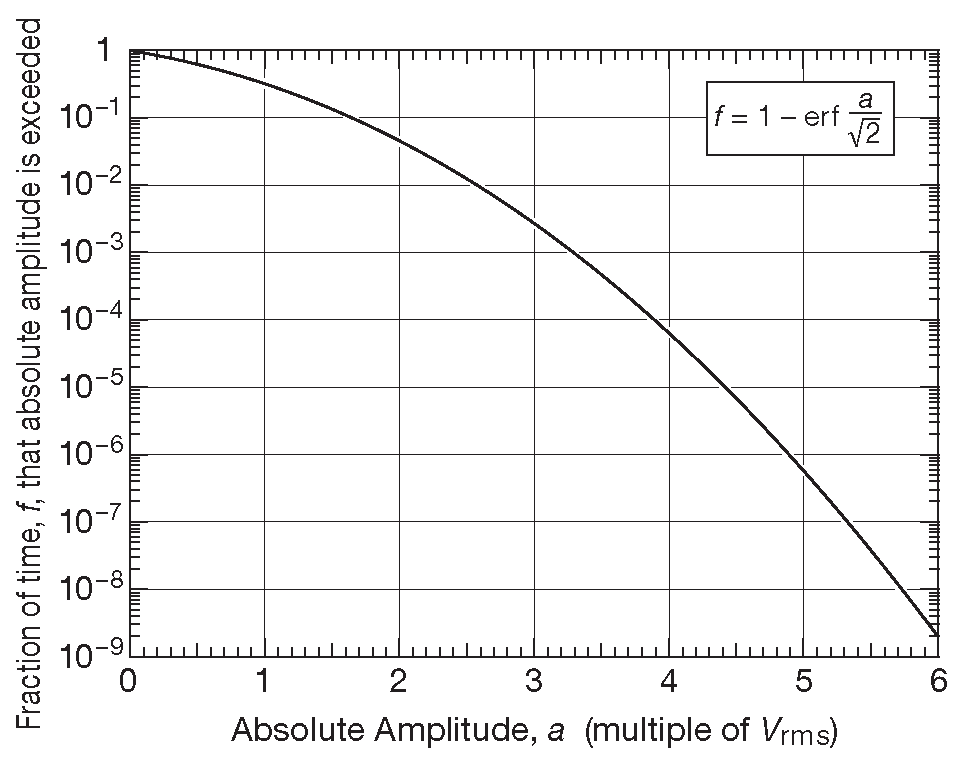
Рис.8.115 Относительная частота появления сигналов определённого уровня в гауссовом шуме. Она может быть полезна для оценки ожидаемого числа ложных срабатываний триггеров, требуемая величина коэффициента формы при RMS-измерениях и т.п.

Частота превышения верхнего порогового уровня шумом с гауссовым распределением, пропущенного через ФНЧ, в единицах среднеквадратического напряжения: \[ \mathrm{TCR}=\frac{\mathrm{BW}}{\sqrt{3}}\exp{\left[\frac{-V_{th}^2}{2}\right]} \qquad \mathrm{events/second} \qquad [8.63] \] где $ V_{th}$ - пороговое напряжение, а BW - полоса идеального ФНЧ ¹³⁸.
Стандартное отклонение шума, вызванное ошибкой квантования: \[ \sigma_n=\frac{\mathrm{LSB}}{2\sqrt{3}}≈ 0.3\mathrm{LSB} \qquad \qquad \qquad \qquad [8.64] \]

==574

¹²⁵ Очень важно отличать описанную только что операцию по усреднению сигнала на промежутке T при измерении статических сигналов от использования временного окна ( опять же, длительности T ), ограничивающего интервал измерения переменного сигнала. В последнем случае речь идёт об использовании «прямоугольного окна», фиксирующего разрешение по полосе BW=1/T ( т.е. в два раза шире, чем при измерении постоянных сигналов ). В цифровой обработке сигналов выбор формы окна играет важную роль, см. Harris, E. J., “On the use of windows for harmonic analysis with the discrete Fourier transform”, Proc. IEEE 66 51-83 ( 1978 ). Синхронное усреднение сигналов ( §8.14 ) имеет те же цели: синхронное детектирование сигнала на промежутке времени T приводит к такому же сужению полосы BW=1/T . <-

¹²⁶ В соответствии с формулой $\cos x\cos y=\space^{1}/_{2}[\cos(x+y )]$+$\space^{1}/_{2}[\cos(x-y )]$ , где $x$=2$πf_{in}$ , а $y$=2$πf_{LO}$ . <-

¹²⁷ В качестве примера, в FM радиоприёмнике LO настраивается на 10.7 MHz ниже нужной станции, а вся работа по демодуляции и усилению проходит на промежуточной частоте 10.7 MHz . Способы работы с радиочастотными сигналами и техника связи подробно обсуждаются в Части_13 второго издания этой книги. <-

¹²⁸ Снова Джейсон Галиччо ( Jason Gallicchio). <-

¹²⁹ Считать формулы и строить итоговые графики удобнее всего в программах электронных таблиц. <-

¹³⁰ В ходе измерений было округлено 100 спектров мощности по 2000 секунд каждый. Это был не самый быстрый эксперимент! <-

¹³¹ Адам Дэр «Считая электроны: как мерить токи в аттоамперном диапазоне», Adam Daire, “Counting electrons: how to measure currents in the attoampere range”, Keithley Instruments, Inc., September 2005. <-

¹³² Бывшее инструментальное подразделение Ithaco Inc. <-

¹³³ Звучит довольно глупо, но на самом деле это предпочтительный метод ( двойное согласованное измерение ), используемый в малошумящих приложениях, например, усилителях для фотодиодов или для CCD-матриц, где тепловой шум резистора обратной связи совершенно неприемлем. (Инженер скажет, что у конденсатора нет теплового шума, физик, что у него может быть в среднем «kT» тепловой энергии, но в отсутствии теплопередачи её уровень не меняется ). Этот приём придумал Харвин ( Garwin ), который использовал его в 1950-х в физических экспериментах, а затем в 1969 для считывания данных с матрицы изображения ( где Харвин давал указание «считывать дважды, чтобы скомпенсировать kT». <-

¹³⁴ В буквальном смысле! Данное утверждение легко проверить: достаточно сделать несколько выдохов внутрь корпуса и померить ток через $R_S$ . Влага из выдыхаемого воздуха оседает в виде конденсата, появляются пути утечки, и ток увеличивается в 20 раз. Через несколько минут - после высыхания поверхностей - уровень подавления восстанавливается. Это причина появления на «высокоомных остеклованных» резисторах фирмы Welwyn защитного проводящего кольца, которое следует подсоединять к земле ( как на схеме ), чтобы блокировать внешние пути утечек. В таком включении отсутствует падение напряжения на участке от корпуса между защитным кольцом до суммирующей точки ( на самом деле оно всё же есть и равно напряжению смещения ОУ, т.е. милливольт или меньше ). Нет падения напряжения - нет тока утечки. «Дыхательный тест» подтвердил данное предположение. <-

¹³⁵ Самое смешное, верным как всегда оказалось самое невероятное предположение. <-

¹³⁶ Какой заряд накопит стержень из кошки, натёртый стекловатой? Or is it a cat being rubbed with glass wool? <-

¹³⁷ Которая заполнена вспененным наполнителем. Этот очень удобный материал используется для изготовления проводящих экранирующих уплотнителей. Самоклеящиеся компоненты вида «ткань поверх пены» выпускает Laird Technologies, см., например, их прямоугольный (4046 ) или полукруглый (4283 ) профили. <-

¹³⁸ Для частоты перехода через симметричные верхний и нижний пороговые уровни ( т.е. частота, при которой размах сигнала превышает заданный уровень $ V_{th}$ ) равна удвоенной, по сравнению с формулой, величине. Спасибо Филу Хоббсу за этот факт, обнаруженный наравне со многими другими на странице 551 его отличной книги. <-

1-полюсный RC	\(e_n^2\frac{π}{2}\frac{f_2^2}{f_1+f_2}\)	\(e_{n2}^2\frac{f_2^3}{f_2^2-f_1^2}\ln\frac{f_2}{f_1}\)	\(e_{n2}^2\frac{π}{2}\frac{f_2^3}{f_1( f_1+f_2 )}\)
Тип фильтра	«Цвет» шума
	Белый	Розовый	Красный
	\(e_n=const\)	\(e_n∼1/\sqrt{f}\)	\(e_n∼1/f\)
идеальный	\(e_n^2( f_2-f_1\) )	\(e_{n2}^2f_2\ln\frac{f_2}{f_1}\)	\(e_{n2}^2\frac{f_2}{f_1}( f_2-f_1\) )
2-полюсный Баттерворта	\(e_n^2\frac{π}{2\sqrt{2}}\frac{f_2^4}{( f_1+f_2 )( f_1^2+f_2^2 )}\)	\(e_{n2}^2\frac{f_2^5}{f_2^4-f_1^4}\ln\frac{f_2}{f_1}\)	\(e_{n2}^2\frac{π}{2\sqrt{2}}\frac{f_2^5}{f_1( f_1+f_2 )( f_1^2+f_2^2 )}\)
m-полюсный Баттерворта	\(e_n^2\frac{π/2m}{\sin(π/2m)}\frac{f_2-f_1}{1-( f_1/f_2 )^{2m}}\)	\(e_{n2}^2\frac{f_2}{1-( f_1/f_2 )^{2m}}\ln\frac{f_2}{f_1}\)	\(e_{n2}^2\frac{π/2m}{\sin(π/2m)}\frac{f_2-f_1}{1-( f_1/f_2 )^{2m}}\)