1.7 (II) Импеданс и реактивность
==47
1.7.6 Мощность в реактивных схемах
Мгновенная мощность, поступающая к какому-либо схемному элементу, всегда определяется произведением \( P=V · I\) . Но в реактивных цепях \( V \) и \(I\) не пропорциональны друг другу прямо, и их амплитуды нельзя перемножать непосредственно. В них могут происходить интересные вещи, например, знак произведения может меняться в течение одного цикла переменного тока. На рис. 1.94 это показано в графическом виде. На интервалах «A» и «C» мощность передаётся конденсатору ( хотя и с разной скоростью ), заряжая его. Накопленная энергия возрастает ( мощность - это скорость изменения энергии ). В интервалах «B» и «D» мощность, которая подаётся на конденсатор, отрицательна, т.е. он разряжается. Средняя мощность за полный цикл равна нулю. Данное положение верно для любого чисто реактивного элемента - катушки, конденсатора или любого их сочетания. Если вам знакомы интегралы от тригонометрических функций, то следующее упражнение трудностей не вызовет.
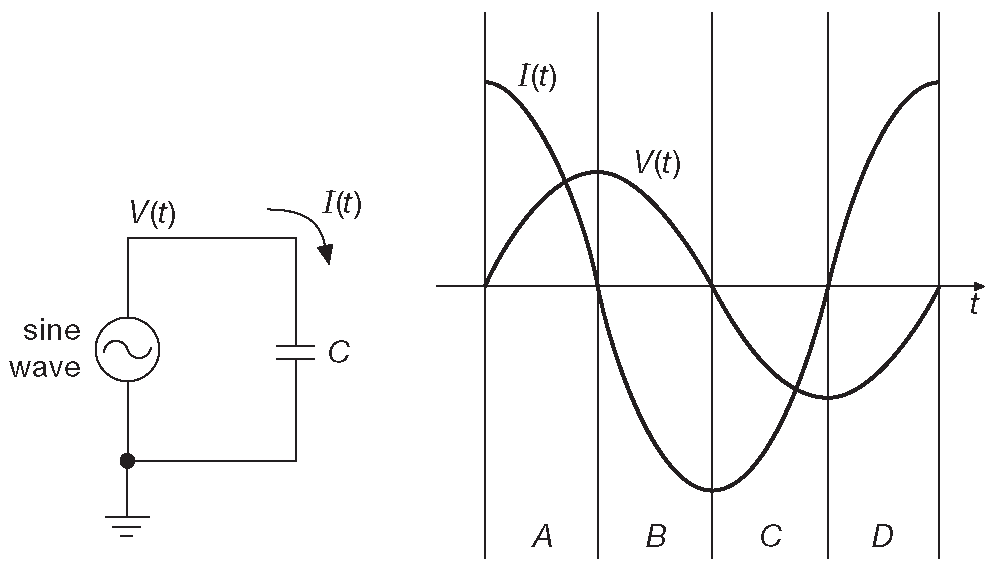
Рис. 1.94 Мощность, подводимая к конденсатору, равна нулю в любой момент времени цикла, благодаря сдвигу фаз между током и напряжением величиной 90°
Упражнение 1.27 ( Дополнительное упражнение )
Докажите, что схема, в которой ток и напряжение не совпадают по фазе на 90° на полном цикле, мощности не потребляет.
Как можно найти среднюю мощность, потреблённую некоторой схемой? В общем случае можно сложить все элементарные произведения \( V · I\) за заданный период времени и поделить на прошедшее время, иначе говоря \[ P = \frac{1}{T}\int_0^T V( t )I( t )dt, \qquad [1.33] \]
где T - время одного полного цикла. К счастью, чаще всего это не требуется, потому что средняя мощность вычисляется по формуле \[ P = \mathscr{Re}(\mathbf{VI^*})=\mathscr{Re}(\mathbf{V^*I}), \qquad [1.34] \]
где \(\mathbf{V}\) и \(\mathbf{I}\) - комплексные амплитуды (rms), а звёздочка обозначает комплЕксное дополнение ( см. Приложение _A [* §A.2 ] , если непонятно о чём речь ).
Пример. Рассмотрим знакомую схему 1.94 . Пусть на конденсатор подаётся синусоидальное напряжение 1 Vrms . Дальнейшие расчёты для простоты будут выполняться с rms амплитудами. \[ \mathbf{V} = 1, \quad \mathbf{I}=\cfrac{\mathbf{V}}{\Big(-\cfrac{j}{ω C}\Big)}=j ω C, \\ P=Re(\mathbf{VI^*})=Re(-j ω C )=0 . \]
Получили нулевую среднюю мощность, что, собственно, и требовалось.
Другой пример. Рассмотрим схему 1.95 .
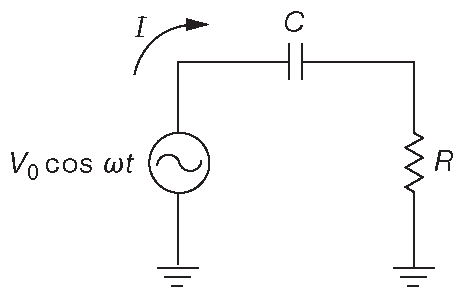
Рис. 1.95 Мощность и коэффициент мощности в последовательной RC цепочке
\[ \begin{align} \mathbf{Z}&=R-\cfrac{j}{ ω C}, \quad \mathbf{V}=V_0, \\ \mathbf{I}&=\mathbf{\cfrac{V}{Z}}= \cfrac{V_0}{R-\cfrac{j}{ω C}}=\cfrac{V_0}{R-\cfrac{j}{ω C}}·\cfrac{\left[R+\left( \cfrac{j}{ω C}\right )\right]}{\left[R+\left( \cfrac{j}{ω C}\right )\right]}= \cfrac{V_0{\left[R+\left( \cfrac{j}{ω C}\right )\right]}}{R^2+\left(\cfrac{1}{ω ^2C^2}\right )} , \\ P&=\mathscr{Re}(\mathbf{VI^*})=\cfrac{V_0^2R}{R^2+\left(\cfrac{1}{ω ^2C^2}\right )}. \end{align} \]
При вычислении тока числитель и знаменатель были умножены на комплексное дополнение знаменателя, чтобы избавиться от его мнимой части в знаменателе [* и отбросили член, включающий «j» ] . Вычисленная мощность 42 меньше, чем простое произведение \(\mathbf{V}\) и \(\mathbf{I}\) , а отношение этих двух мощностей называют коэффициентом мощности . \[ \begin{align} |\mathbf{V}||\mathbf{I}|&=\cfrac{V_0^2}{\sqrt{R^2+\cfrac{1}{ω ^2C^2}}}, \\ pfactor&=\frac{P}{|\mathbf{V}||\mathbf{I}|} = \cfrac{R}{\sqrt{R^2+\cfrac{1}{ω ^2C^2}}} \end{align} \]
Коэффициент мощности - косинус угла между фазами тока и напряжения и меняется от 0 ( чисто реактивная цепь ) до 1 ( чисто резистивная ). Коэффициент мощности, меньший единицы, свидетельствует о наличии в схеме реактивных токов 43 . Стоит отметить, что коэффициент мощности стремится к единице, а рассеиваемая мощности к \( V^2/R\) , когда велика ёмкость или рабочая частота, где реактивная составляющая конденсатора становится сильно меньше \(R\) .
==48
Упражнение 1.28
Покажите, что вся средняя поступающая в схему 1.95 мощность рассеивается на резисторе. Надо вычислить \( V_R^2/R\) . Чему она равна для конденсатора 1 μF и резистора 1 kΩ при напряжении 115 Vrms@60 Hz?
Коэффициент мощности оказывает серьёзное влияние на электрические распределительные сети, потому что реактивные токи не передают мощность в нагрузку, но выливаются в расходы на I2R нагрев активных сопротивлений в линии - проводов, обмоток генераторов и трансформаторов. Частные потребители платят только за «реальную» мощность ( \(\mathscr{Re}(\mathbf{VI^*}\) ) ), а промышленные вынуждены нести расходы на коэффициент мощности. Именно этим объясняются огромные площади, забитые конденсаторами на территориях промышленных предприятий. Они компенсируют индуктивную реактивность электродвигателей станочного парка.
Упражнение 1.29
Покажите, что последовательно включённый конденсатора \( C=1/(ω^2L) \) доводит коэффициент мощности последовательной RL цепи до 1.0 . Проведите расчёты для цепи, где термин «последовательный» заменён на «параллельный».
1.7.7 Обобщение делителя напряжения
Обычный делитель напряжения ( рис. 1.6 ) состоит из пары последовательных резисторов, заземлённых с одного конца. Его вход наверху, а выход в средней точке. Обобщённая схема этой простой цепи имеет на месте каждого из резисторов R, L или C ( или более сложную [* двухвыводную] цепь, состоящую из сочетания упомянутых R, L, C ), как на рис. 1.96 . В общем случае отношение \( V_{out}/V_{in}\) такой схемы константой не является, а зависит от частоты, как, например, это происходит в фильтрах низких и высоких частот ( §1.7.1 ). Анализ очевиден:
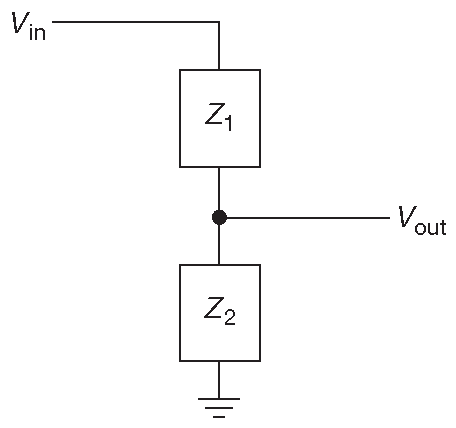
Рис. 1.96 Обобщённый делитель напряжения: пара каких-то импедансов
\[ \mathbf{I}=\mathbf{\frac{V_{in}}{Z_{total}}}, \quad \mathbf{Z_{total}}=\mathbf{Z_1+Z_2}, \\ \mathbf{V_{out}}=\mathbf{IZ_2}=\mathbf{V_{in}\frac{Z_2}{Z_1+Z_2}}. \]
Рассмотрим простые, но очень важные примеры, начиная с RC ФВЧ и ФНЧ, приближённые расчёты по которым проводились ранее.
1.7.8 RC фильтр высоких частот
Ранее было показано, что, используя изменение импеданса конденсатора по частоте \(\mathbf{Z_C}=-\frac{j}{ ω C}\) , можно собрать из конденсатора и резистора частотно зависимый делитель напряжения. Получившаяся схема способна пропускать интересующие частоты и задерживать нежелательные. В этом и следующем параграфе будут вновь рассмотрены простые фильтры верхних и нижних частот, а расчёты, сделанные в §1.7.1 , будут исправлены. Это простые, но очень важные и очень активно используемые узлы электронных схем. Подробнее фильтры рассматриваются в Части _6 и Приложении _E .
Возвращаясь к классическому RC фильтру высоких частот ( рис. 1.92 ), можно заметить, что обобщённый закон Ома ( уравнения для делителя в комплексных числах ) даёт следующее соотношение: \[ \mathbf{V_{out}}=\mathbf{V_{in}}\frac{R}{R-\cfrac{j}{ω C}}=\mathbf{V_{in}}\cfrac{R\left( R+\cfrac{j}{ω C}\right )}{R^2+\cfrac{1}{ω ^2C^2}}. \]
(На последнем шаге числитель и знаменатель были домножены на комплЕксное дополнение знаменателя. ) Чаще всего интересна не фаза \( V_{out}\) , а только его амплитуда: \[ V_{out}= \sqrt{\mathbf{V_{out}V^*_{out}}}= V_{in}\frac{R}{\sqrt{R^2+\cfrac{1}{ω ^2C^2}}}. \]
Результат очень похож на выражение для резистивного делителя: \[ V_{out} = V_{in}\frac{R_2}{R_1+R_2}. \]
==49
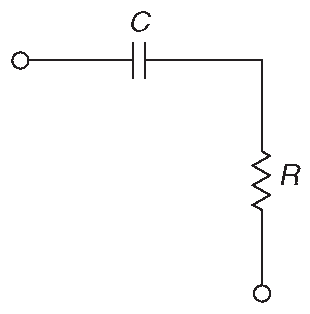
Рис. 1.97 Фильтр высоких частот без нагрузки
Импеданс последовательной RC цепочки ( рис. 1.97 ) показан [* в векторной форме на комплексной плоскости ] на рис. 1.98 . Её отклик, если не учитывать сдвиг фаз и брать только модули комплексных амплитуд, равен:
\[ V_{out}=V_{in}\frac{R}{\sqrt{R^2+\cfrac{1}{ω ^2C^2}}}=V_{in}\frac{2 π fRC}{\sqrt{1+( 2 π fRC )^2}}, \qquad [1.35] \] а выглядит, как на рис. 1.99 ( и на рис. 1.91 ).
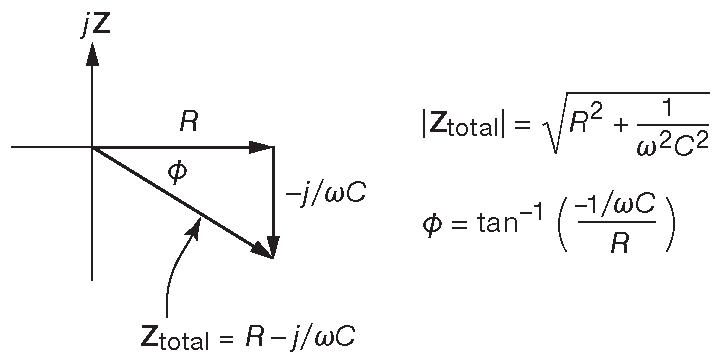
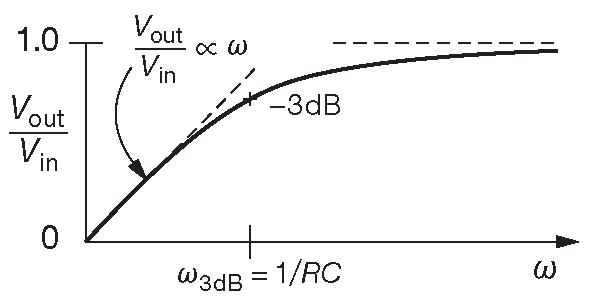
Рис. 1.98 Импеданс последовательной RC цепи [* в формуле используется западная форма записи для функции \( ϕ=\arctan()\) ]
Рис. 1.99 Частотный отклик [* АЧХ ] фильтра высоких частот. Соответствующий сдвиг фаз плавно меняется от +90° ( на частоте \(ω=0\) ), через +45° ( на \(ω_{3dB}\) ) и до 0° ( на \(ω = ∞\) ). Аналогично ведёт себя и фильтр нижних частот ( рис. 1.104 )
Отметим, что можно было бы получить этот результат сразу, взяв отношение модулей комплексных импедансов, как в упражнении 1.26 и примере перед ним. Числитель - импеданс нижнего плеча делителя ( R ), знаменатель - величина последовательного соединения импедансов R и C.
Как отмечалось ранее, на высоких частотах выход примерно равен входу ( насколько высоких, спрашиваете? Выше \(ω ≳ \frac{1}{RC}\) ) и равен нулю на низких частотах. Фильтры высоких частот очень активно используются. Например, вход осциллографа можно переключить в положение «связь по переменному току». Т.е. сигнал будет проходить как раз через RC фильтр высоких частот со срезом порядка 10 Hz . ( Такой режим нужен, чтобы наблюдать малый сигнал с большим постоянным смещением [* например, пульсации блока питания] ). В инженерной среде принято использовать точку «-3dB» на АЧХ фильтра ( или любого устройства, ведущего себя сходным образом ). В случае простого RC фильтра высоких частот точка «-3dB» находится по формуле \[ f_{3dB} = \frac{1}{2 π RC}. \]
==50
Часто требуется узнать импеданс конденсатора на некоторой частоте ( например, при расчёте всё того же фильтра ). На рис. 1.100 приведена удобная номограмма, закрывающая большой диапазон емкостей и индуктивностей, по которой можно узнать величину \[|\mathbf{Z}|=\frac{1}{2 π RC}\] .
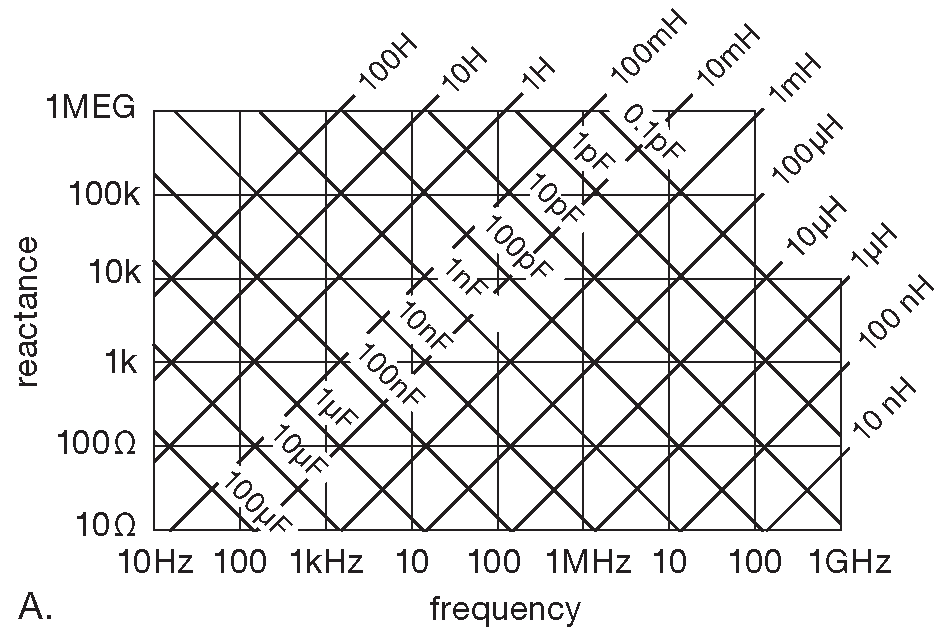
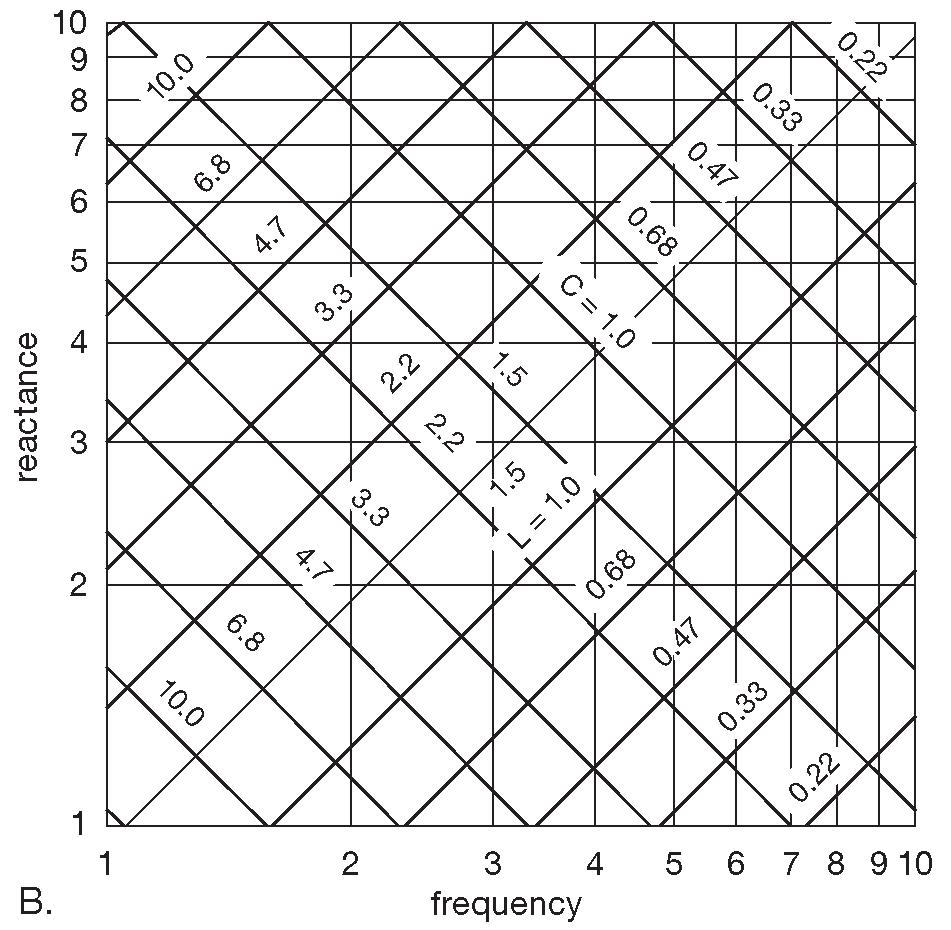
Рис. 1.100 (A) Реактивное сопротивление катушек и конденсаторов в зависимости от частоты. Декады различаются только множителем. (B) Одна декада из графика A в увеличенном виде с номиналами из стандартного 20-процентного ряда ( EIA “E6”). [* См. §С.2 ]
В качестве примера рассмотрим схему на рис. 1.101 . Это фильтр высоких частот с точкой «3dB» 44 на 15.9 kHz . Импеданс на выходе должен быть гораздо выше 1.0 kΩ , чтобы исключить воздействие на параметры схемы, а источник сигнала должен работать на нагрузку 1.0 kΩ без существенной потери амплитуды ( см. разбор граничных условий для работы RC фильтров в §1.7.1.D .
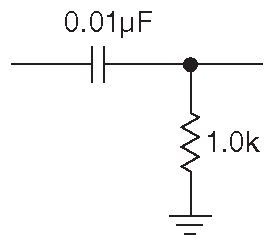
Рис. 1.101 Пример фильтра высоких частот
1.7.9 RC фильтр низких частот
Разберём опять фильтр низких частот ( в нём R и С поменяны местами ) с симметричной реакцией ( рис. 1.90 и 1.102 ). Точное соотношение
\[ V_{out} = V_{in}\frac{1}{\sqrt{1+ ω ^2R^2C^2}}. \qquad [1.36] \]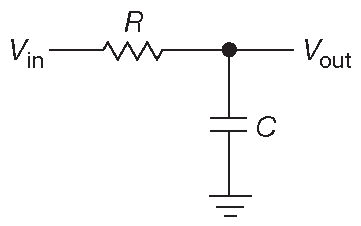
Рис. 1.102 Фильтр низких частот
Точка «3dB» опять на частоте \( f=\frac{1}{2 π RC}\) ( рис. 1.103 и 1.91 ) 45 . Фильтры низких частот также широко применяются в жизни, например, с их помощью можно подавить интерференцию от близлежащих телевизионных станций ( 500 kHz...800 MHz ), мешающих работе звуковых усилителей и прочей чувствительной электроники.
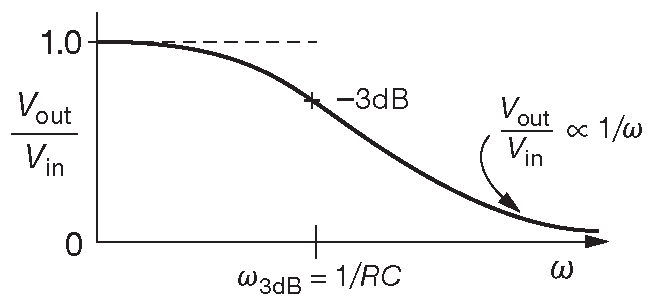
Рис. 1.103 АЧХ фильтра низких частот
Упражнение 1.30
Покажите, что формула [1.36] корректна.
Выход ФНЧ, работающий источником сигнала, имеет свои особенности. Для сигнала переменного тока с идеального источника ( с нулевым выходным импедансом ) на низких частотах вЫходной импеданс фильтра выглядит как сопротивление \(R \) . (Для подсчёта импеданса идеальный источник можно заменить короткозамкнутой цепью ). На высоких частотах, где доминирует конденсатор, вЫходной импеданс падает до нуля. Источник сигнала видит фильтр как резистор \(R \) + «нагрузка-после-фильтра» на низких частотах, или как просто \(R \) на высоких. В §1.7.1.D отмечалось, что в худшем случае импеданс RC фильтра ( и низких, и высоких частот ) в любом направлении составляет \(R \) .
==51
На рис. 1.104 изображён отклик фильтра низких частот в логарифмических координатах - это наиболее активно используемое представление. В таком виде по вертикали получаются децибелы, а по горизонтали - октавы или декады. На таком графике равные расстояния соответствуют равным отношениям. Сдвиг фаз рисуется с линейной вертикальной осью ( градусы ) и логарифмической осью частот. [* Данная пара графиков называется «диаграммой Боде»] . Такие графики удобнее использовать, если нужно разобрать детали при сильном изменении амплитуды. Довольно много их можно найти в Части _6 , где рассматриваются активные фильтры. Отметим, что экспоненциальное изменение амплитуды превращается в логарифмических координатах в прямую линию с наклоном –20 dB/decade ( в инженерной среде предпочитают форму –6 dB/octave ). Отметим также, что сдвиг фазы плавно меняется от 0° ( на частоте много ниже среза ) до –90° ( гораздо выше среза ), а значение –45° - точке «-3dB». Эмпирическое правило для RC фильтров: сдвиг фазы составляет примерно 6° в точках 0.1\( f_{3dB} \) и 10\( f_{3dB} \) .
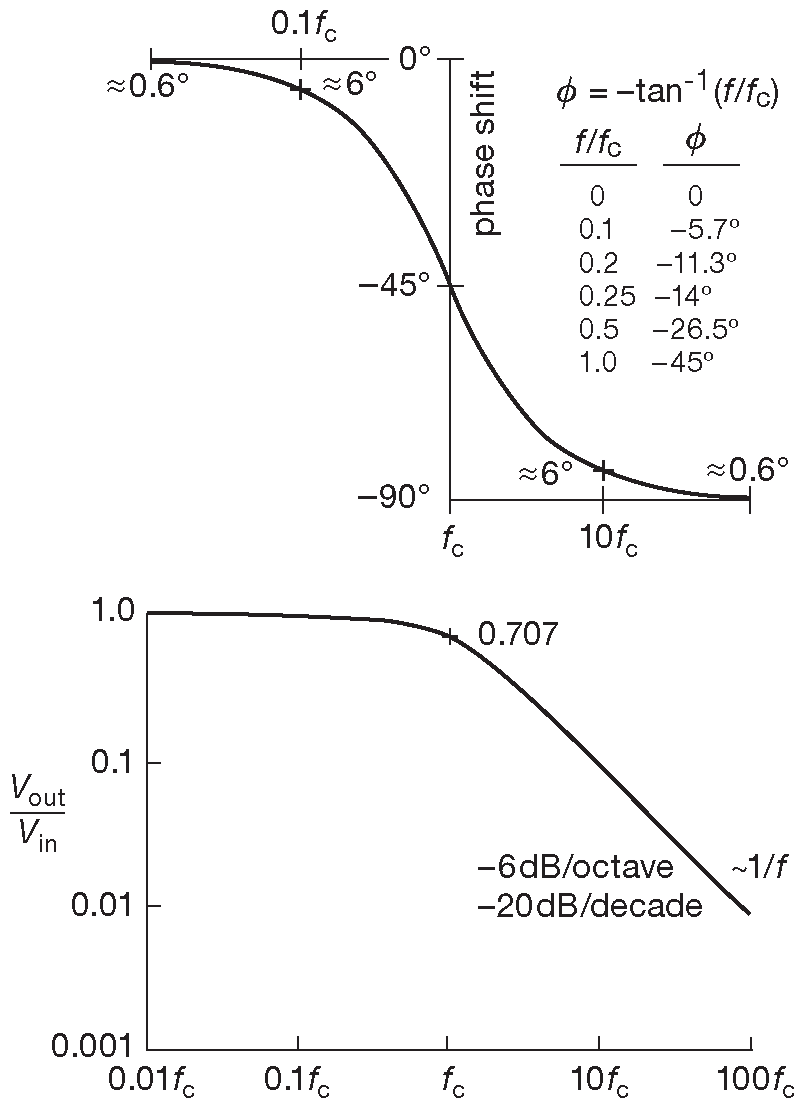
Рис. 1.104 Амплитудная и фазовая характеристики ФНЧ в логарифмических координатах. Отметим, что в точке «-3dB» сдвиг фазы равен –45° , а на частотах, отстоящих от неё на порядок в обе стороны, составляет примерно 6°
Упражнение 1.31
Подтвердите данное правило.
С фильтрами связан интересный вопрос. Можно ли создать фильтр с заданной амплитудой и заданной фазой на некоторой частоте? Довольно неожиданно, но, нет. Соотношения между фазой и амплитудой в физически реализуемых фильтрах определяются причинно-следственной связью ( т.е. реакция должна следовать за воздействием, а не наоборот ). Официальное название такой зависимости – «соотношения Крамерса-Кронига» .
1.7.10 RC дифференциаторы и интеграторы в частотной области
RC дифференциатор, знакомство с которым произошло в §1.4.3 , в точности то же, что и фильтр высоких частот, описанный в этой главе. Его можно рассматривать, как и раньше, либо в виде сигнала некоторой формы во временной области, либо как набор гармонических компонент в частотной [* в виде характерной «гребёнки» из пиков, раскиданных по оси частот] . Следует напомнить условия правильной работы, объявленные ранее для временной области ( \( dV_{out} ≪ dV_{in}\) ), но подправленные для частоты: чтобы выходной сигнал был мал по отношению ко входному, частота ( или частоты ) сигнала должна быть много ниже точки «3dB». Проверить его выполнение легко. Предположим, есть входной сигнал \( V_{in}=\sin( ωt) \) . Используя выведенные ранее соотношения для дифференциатора, имеем: \[ V_{out} = RC\frac{d}{dt}\sin( ω t ) = ω RC\cos( ω t ), \] тогда условие \( dV_{out} ≪ dV_{in}\) выполняется, если \(ω RC ≪ 1\) , т.е. \(RC ≪ \frac{1}{ ω }\) . Если во входном сигнале имеется набор частот, то данное условие должно выполняться для самой высокой из них.
RC интегратор ( §1.4.4 ) - то же самое, что фильтр низких частот. По сходным причинам интегратор будет работать хорошо, если самая низкая частота входного сигнала будет лежать гораздо выше точки «-3dB».
1.7.11 Катушки индуктивности вместо конденсаторов
Фильтры низких ( высоких ) частот можно строить на резисторах и катушках вместо конденсаторов. На практике встретить RL фильтр можно нечасто. Причина в бОльших, как правило, габаритах катушек и не столь хороших итоговых электрических параметрах ( индуктивные элементы дальше отстоят от идеала, нежели конденсаторы, см. Часть X1 [* ##§X1.3 и ##§X1.4 ] ). Если можно выбирать, используйте конденсатор. Единственным важным исключением является использование ферритовых бусин и дросселей на высоких частотах. Раскиданные там и сям по схеме они чуть увеличивают индуктивность соединений. Это ведёт к подъёму импеданса цепей на высокой частоте, подавляя самовозбуждение, но сохраняя низкое активное сопротивление связи, чего нельзя было бы добиться с RC фильтром. Дроссели - катушки индуктивности, состоящие из нескольких витков провода на ферритовом сердечнике, выполняющие те же функции в радиочастотных схемах. Отметим, что катушки индуктивности - необходимые элементы
1.7.12 Векторная диаграмма токов и напряжений
Есть весьма наглядный графический метод, который может быть полезен при изучении реактивных цепей. Разберём, для примера, RC фильтр, ослабляющий сигнал на «3dB» в точке \( f=\frac{1}{2 π RC}\) ( §1.7.8 ). Данное положение верно и для ФНЧ, и для ФВЧ. Здесь легко ошибиться, ожидая, что, раз в данной точке реактивное сопротивление равно сопротивлению резистора, то ослабление составит 6 dB ( т.е. 1/2 ). Это было бы верно, если бы на месте конденсатора был резистор с активным сопротивлением, равным импедансу конденсатора. Ошибка возникает, потому что конденсатор - реактивный элемент, что хорошо видно на векторной диаграмме ( рис. 1.105 ). На одной из осей откладывается действительная ( резистивная ) компонента импеданса, на другой - мнимая ( реактивная ). В последовательных цепях оси отражают также комплексное напряжение, потому что ток во всех точках таких цепей одинаков. В примере ( будем рассматривать его как RC делитель напряжения ) входное напряжение прикладывается к гипотенузе, а выходное снимается с R. Диаграмма соответствует частоте, на которой реактивное сопротивление конденсатора равно по абсолютной величине R, т.е. \( f=\frac{1}{2 π RC}\) . По диаграмме видно, что отношение выходного напряжения ко входному равно 1/\(\sqrt2\) или 3 dB .
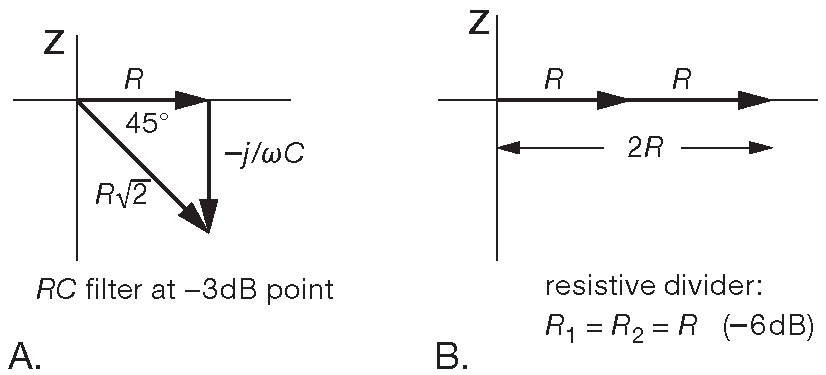
Рис. 1.105 Векторная диаграмма фильтра низких частот в точке «-3dB»
==52
Угол между векторами равен сдвигу фазы от входа к выходу. В точке «3dB», например, выходная амплитуда эквивалентна входной, делённой на \(\sqrt2\) , а фаза опережает входную на 45° . Такой графический метод наглядно показывает соотношение амплитуд и фаз в RLC схемах. Её можно использовать для изучения фильтра высоких частот, разобранного ранее аналитически.
Упражнение 1.32
Используя векторную диаграмму, разберите работу RC фильтра высоких частот, для которого \( V_{out}=V_{in}\frac{R}{\sqrt{R^2+\frac{1}{ω ^2C^2}}}\) .
Упражнение 1.33
На какой частоте RC фильтр низких частот ослабляет входной сигнал на 6 dB ( т.е. в 2 раза )? Какой при этом сдвиг фаз?
Упражнение 1.34
Используя векторную диаграмму, рассмотрите работу фильтра низких частот, разобранного ранее аналитически.
В §2.2.8 будет показан симпатичный пример использования векторной диаграммы в приложении к схеме поворота фазы с выходом постоянной амплитуды.
1.7.13 «Полюса» и «децибелы на октаву»
Взглянем ещё раз на АЧХ RC фильтра низких частот ( рис. 1.103 и 1.104 ). Достаточно далеко от «колена» выходная амплитуда падает пропорционально 1/\( f \) . За одну октаву ( за октаву частота изменяется в два раза ) выходная амплитуда падает в 2 раза, т.е. изменяется на –6 dB . Иначе говоря, простой RC фильтр имеет спад 6 dB/octave . Можно составить несколько RC секций и получить 12 dB/octave для двух или 18 dB/octave для трёх и т.д. «Децибелы на октаву» один из активно применяемых терминов для описания фильтров. Другой метод - указание числа «полюсов», т.е. «трёхполюсный», если речь идёт о трёх последовательных RC секциях. Термин «полюс» используется в теории цепей, описание которой выходит за рамки книги. Она предполагает комплексные преобразования функций передачи на комплексной же плоскости, известной как S-пространство . Тема объясняется чуть подробнее в Части X1 [* ##§X1.5 ] .
С многокаскадными фильтрами следует соблюдать осторожность. Их нельзя просто соединять друг с другом, рассчитывая, что результат будет идентичен сумме действий отдельных фильтров. Проблема в том, что при таком включении фильтры будут существенно влиять друг на друга ( они же одинаковые ), меняя общий результат. Аналитический вывод сделанный ранее предполагает источник с нулевым и приёмник с бесконечным импедансом. Одним из решений будет создание последовательных секций фильтра с существенно увеличенным относительно предыдущих импедансом. Гораздо лучше использовать промежуточные «буферные» каскады на транзисторах или операционных усилителях или переходить на активные фильтры. Эта объёмная тема затрагивается в Части _2 , _3 , _4 , _6 и 13 .
1.7.14 Резонансные схемы
Конденсаторы в паре с катушками индуктивности или в составе активных фильтров позволяют получить схемы с очень резкими частотными характеристиками ( т.е. высокий пик в ответ на конкретную частоту ), если сравнивать с плавными изгибами уже рассмотренных RC звеньев. Такие схемы находят применение в различных звуковых и радиочастотных устройствах. Здесь будет сделан общий обзор LC цепей ( тема продолжается в Части _6 и Приложении _E ).
1.7.14.A Параллельные и последовательные LC цепи
==53
Для начала разберём схему 1.106 . Импеданс параллельной LC цепи на частоте \( f \) составит \[ \begin{align} \frac{1}{Z_{LC}}&=\frac{1}{Z_L}+\frac{1}{Z_C}= \frac{1}{j ω L}-\frac{ ω C}{j}=j\left( ω C-\frac{1}{ ω L}\right ), \\ Z_{LC}&=\cfrac{j}{\cfrac{1}{ ω L}-ω C} \end{align} \]
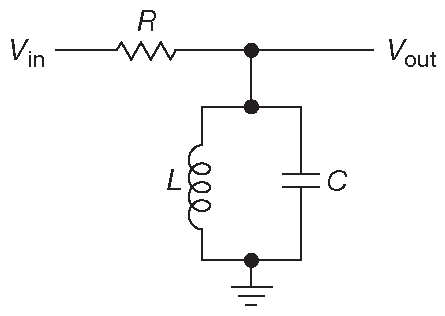
Рис. 1.106 Резонансная LC схема - полосовой фильтр
Этот импеданс образует с R делитель напряжения. С изменением частоты катушка и конденсатора ведут себя противоположным образом, поэтому на резонансной частоте импеданс LC цепи становится бесконечным. \[ f_0 = \frac{1}{2 π \sqrt{LC}}, \qquad [1.37] \] т.е. на частоте \(ω_0=\frac{1}{\sqrt{LC}}\) АЧХ будет иметь пик ( рис. 1.107 ).
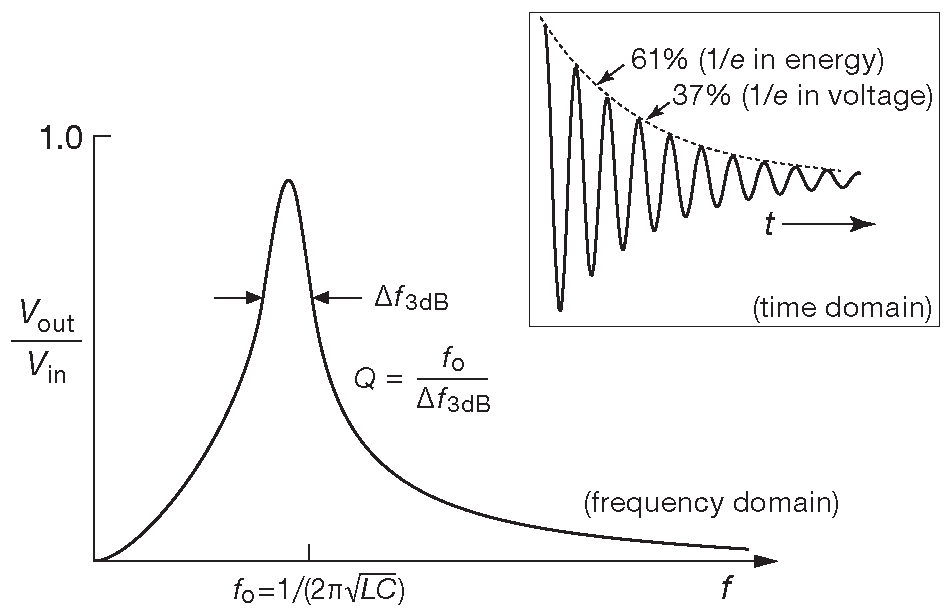
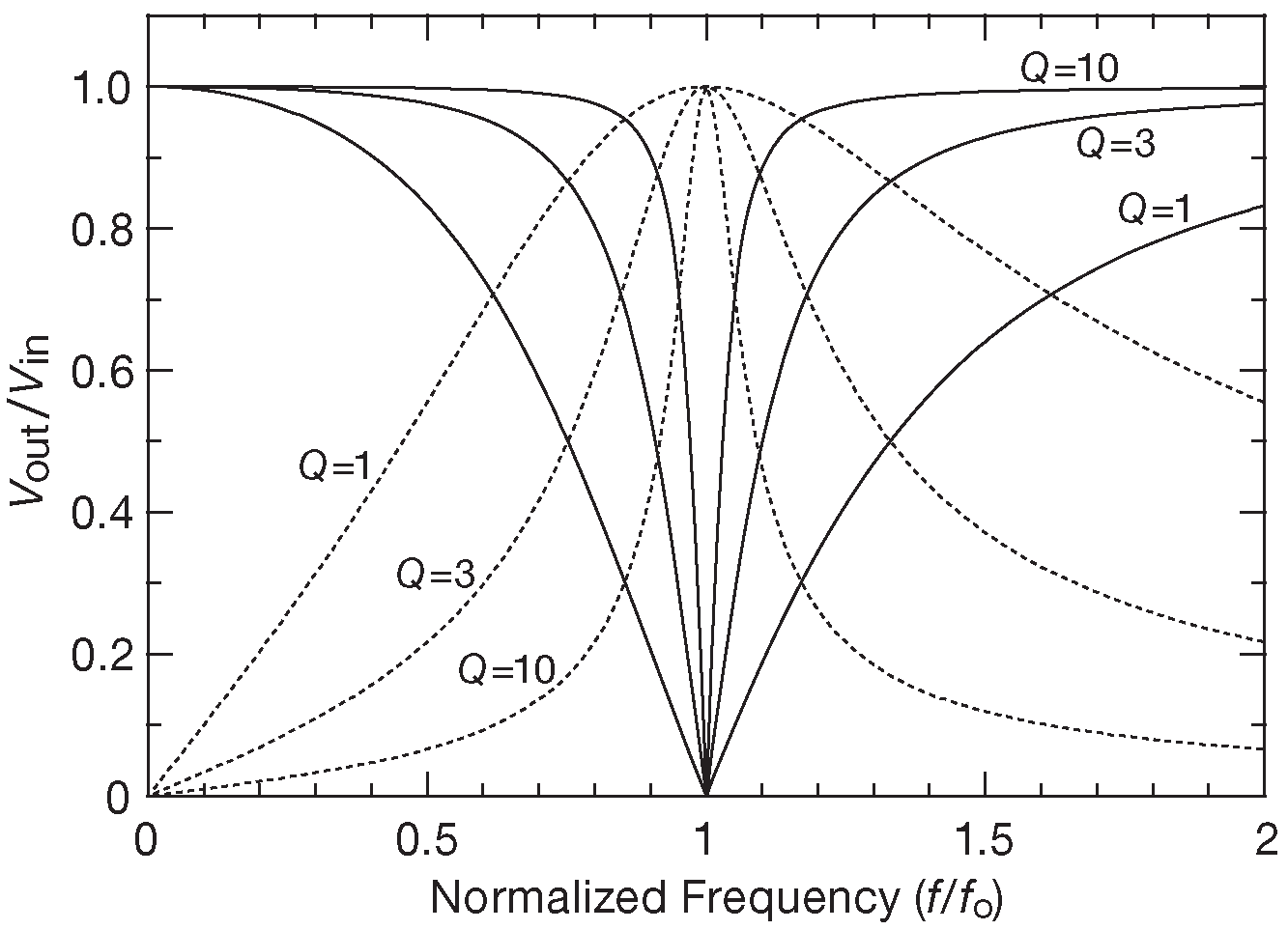
Рис. 1.107 Частотная характеристика параллельного LC контура . На врезке показано поведение схемы во временной области: демпфированная генерация ( «звон» ) возникает на каждом фронте входного сигнала
Рис. 1.110 АЧХ параллельных ( пунктир ) и последовательных ( сплошная линия ) LC цепей для нескольких значений добротности Q
На практике острота пика ограничивается потерями в катушке и конденсаторе, но хорошая конструкция может снизить их очень заметно. Соответственно, снижающий добротность резистор иногда добавляют намеренно, чтобы расширить резонансный пик. Данная схема известна как «резонансный контур» и активно используется в радиочастотных устройствах для выбора заданной частоты усиления ( катушки и конденсаторы бывают переменные, позволяя подстроить частоту ). Чем выше импеданс источника, тем острее пик. Достаточно распространённой практикой является использование схем, напоминающих источники тока, которые будут показаны позднее. Добротность Q - величина, позволяющая оценить остроту пика. Она равна резонансной частоте, делённой на ширину по уровню «-3dB». Для параллельных RLC схем Q=\(ω_0 RC\) 46 .
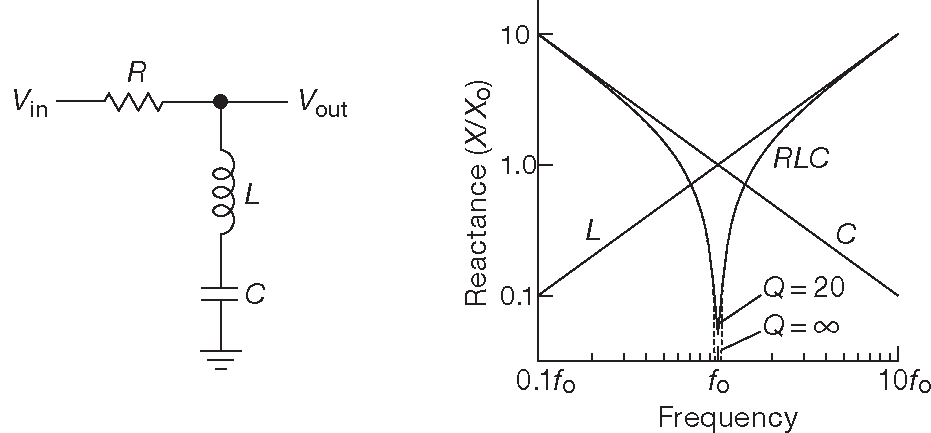
Рис. 1.108 Режекторный LC фильтр. График для реактивных сопротивлений катушки и конденсатора показан справа, но следует учитывать, что их комплексные импедансы имеют противоположные знаки, вызывая резкий спад общего импеданса цепи. Для идеальных компонентов реактивное сопротивление последовательной LC цепи на частоте резонанса равно нулю. Для реальных компонентов до нуля он не доходит и определяется активным сопротивлением катушки
Другой разновидностью резонансных схем является последовательная LC цепь ( рис. 1.108 ). Выписав нужные формулы импедансов и предполагая конденсатор и катушку идеальными компонентами, т.е. отсутствие резистивных потерь 47 , можно обнаружить, что импеданс на резонансной частоте ( \( f_0=\frac{1}{2 π \sqrt{LC}}\) ) становится нулевым. Такая цепь является «ловушкой» для сигналов рядом с частотой резонанса, потому что закорачивает их на землю. Основным местом использования вновь являются радиочастотные схемы. Частотная характеристика показана на рис. 1.109 . Добротность последовательной RLC цепи равна Q=\(ω_0 ( L/R\) ) 48 . Влияние величина Q на форму АЧХ можно посмотреть на рис. 1.110 .
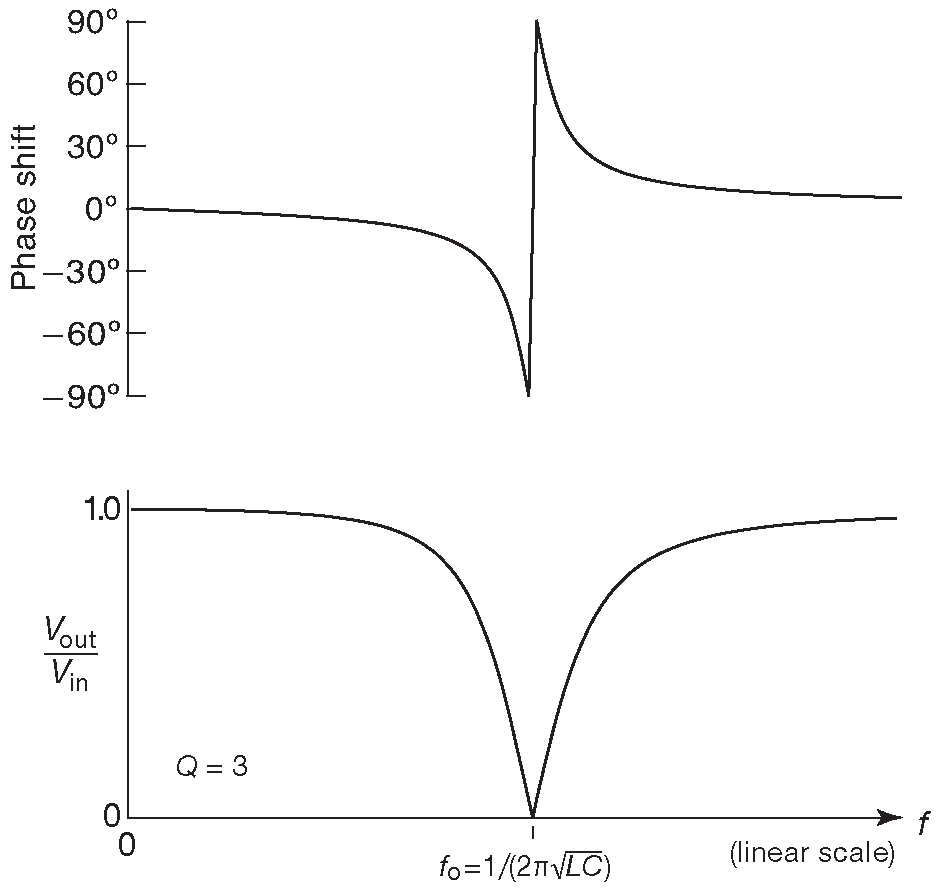
Рис. 1.109 Амплитудно- и фазочастотная характеристики последовательной LC цепи. На частоте резонанса фаза резко меняется. Тот же эффект можно видеть в других видах резонаторов ( см. рис. 7.36 )
==54
Упражнение 1.35
Найдите зависимость \( V_{out}/V_{in}\) от частоты для последовательной LC схемы с рис. 1.108 .
Резонансные LC схемы описываются в терминах реакции по частоте, т.е. в частотной области. Во временнОй обычно рассматривается реакция на импульс или перепад. Для параллельной LC схемы с Q=20 её можно видеть на врезке на рис. 1.107 . Сигнал спадает до 1/e ( 37% ) за Q/π циклов. Накопленная контуром энергия ( пропорциональная \( V^2\)) падает до 1/e ( 61% от исходной амплитуды ) за Q/(2\(π\)) циклов. Возможно, удобнее будет рассматривать процесс в радианах: энергия падает до уровня 1/e за Q радиан, а напряжение за 2Q радиан. Резонансные LC схемы - не единственные, позволяющие провести частотный отбор. Такими же свойствами обладают кварцевые кристаллы, керамические и ПАВ резонаторы, линии передач и объёмные резонаторы [* например, музыкальные инструменты] .
1.7.15 LC фильтры
Комбинируя катушки и конденсаторы можно создавать фильтры ( полосовые, высоких и низких частот ) с гораздо более резким изломом частотной характеристики, чем можно получить с RC схемами с любым числом каскадов. Эта тема разбирается в Части _6 , но сейчас можно просто восхититься эффективности его работы и оценить достоинства простой катушки индуктивности ( часто незаслуженно критикуемой ).
Взгляните на рис. 1.111 . Это плата «умножителя-оцифровщика», спроектированная несколько лет назад под проект приёмника для радиоастрономии с 250 миллионами (!?) параллельных каналов. На плате много всего, что призвано вдвинуть сигнал по частоте и оцифровать его в трёх частотных полосах. Описание разработки могло бы занять целую часть книги [* к вопросу о числе каналов: в §6.2.3.C говорится о 126 платах, см. также рис. 6.8 , 7.29 ] , но сейчас стоит обратить внимание на фильтр на 1.0 MHz , торчащий среди платы и обведённый овалом ( всего их на плате шесть ). Фильтр собран на трёх подстроечных катушках ( металлические кубики ) и четырёх конденсаторах ( пары ярких прямоугольников ). Его задача - препятствовать появлению внеполосных «фантомных копий» на цифровом выходе. Эта интересная проблема разбирается в Части 13 .

Рис. 1.111 Шесть LC фильтров низких частот на печатной плате - часть схемы преобразования и оцифровки сигнала [* см. рис. 6.8 , 7.29 ]
Насколько хорош фильтр? На рис. 1.112 показан выход генератора синусоидального сигнала «качающейся частоты» с диапазоном 0...2 MHz . Нижняя граница слева экрана, верхняя - справа с плавным переходом частоты по ширине изображения. Самое интересное - волновой «конверт» - огибающая амплитуды синусоидального сигнала [* т.е. та самая «АЧХ»] для двух фильтров с одной частотой среза ( 1 MHz ): LC и RC ( 1 kΩ+160 pF ). LC побеждает с лёгкостью, а RC бледно смотрится на его фоне. В языке нет достаточно точных слов, которые позволили бы описать «срез» RC цепочки. Вряд ли она способна «срезать» что-либо вообще.
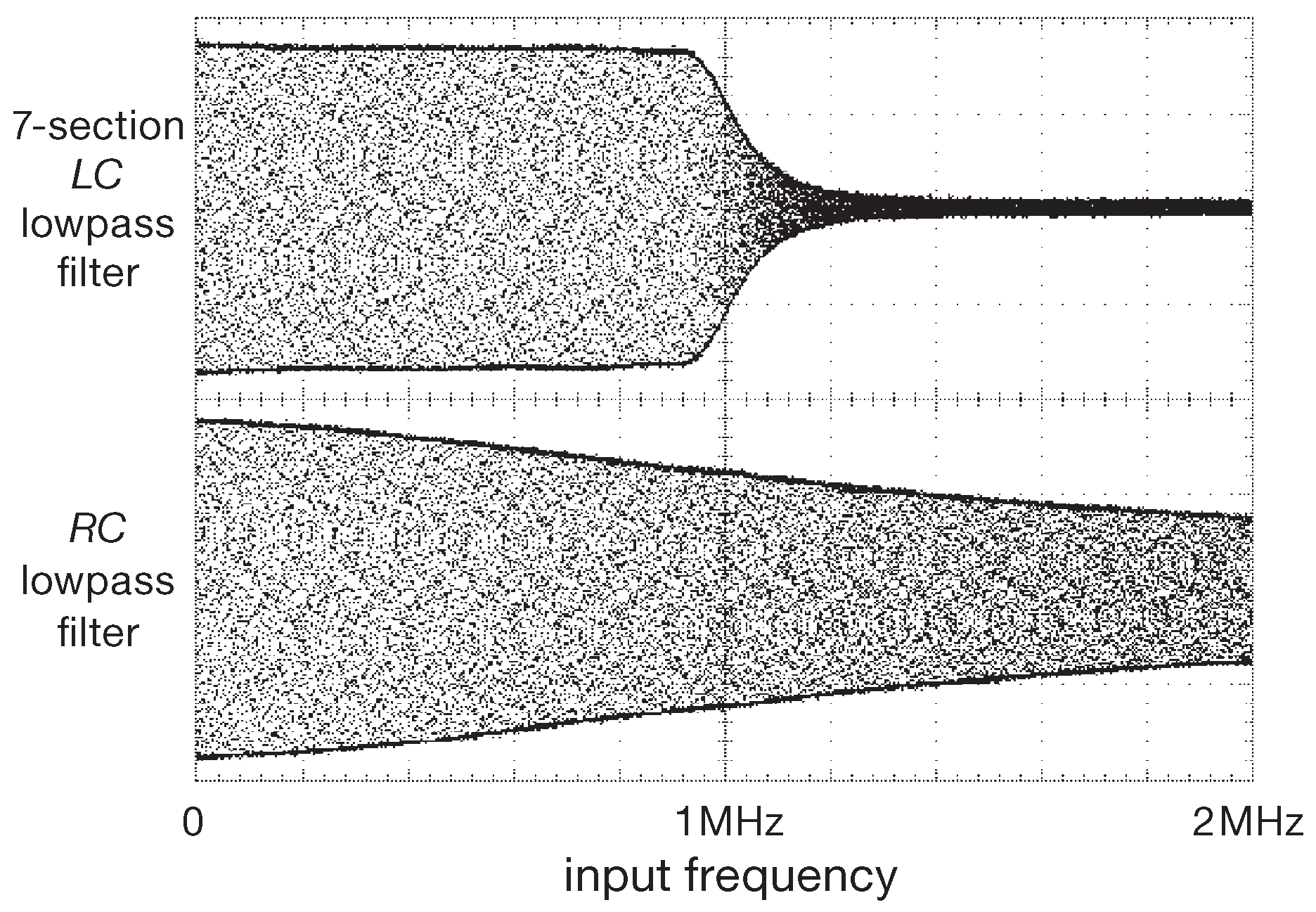
Рис. 1.112 Проверка LC фильтра низких частот с рис. 1.111 с помощью генератора качающейся частоты. Для сравнения приводится АЧХ RC фильтра с такой же частотой среза ( 1 MHz ). Тёмное заполнение - синусоидальный сигнал с непрерывно меняющейся частотой, который на экране цифрового осциллографа превращается в «снег»
1.7.16 Прочие применения конденсаторов
В дополнение к фильтрам, резонансным цепям, дифференциаторам и интеграторам конденсаторы находят применение в иных важных задачах. Задачи эти будут подробно разбираться в других частях, а сейчас просто кратко перечислены для ознакомления.
1.7.16.A Шунтирование
Импеданс конденсатора снижается с увеличением частоты, что позволяет использовать его для шунтирования . Часто возникает необходимость получить в схеме постоянную составляющую, избавившись от переменного сигнала. Шунтирующий конденсатор на выводах компонента ( обычно речь идёт о резисторе ) позволяет убить переменную составляющую в шунтируемой цепи. В таких задачах используется конденсатор, чей номинал совершенно не критичен и должен лишь удовлетворять условию: его импеданс на частоте сигнала должен быть мал по сравнению с импедансом шунтируемой цепи.
==55
1.7.16.B Фильтрация питания
Этот пример встречался в §1.6.3 , где с его помощью уменьшались пульсации с выпрямителя. Разработчики часто называют такие конденсаторы фильтрующими , но на самом деле речь идёт о шунтировании или накоплении энергии в конденсаторах большой ёмкости. В итоге используется термин накопление . Конденсаторы для такой задачи нужны достаточно габаритные. Это объёмистые цилиндры, которые можно найти внутри многих приборов. О питании электронных схем рассказывает Часть _9 .
1.7.16.C Генерация сигналов и получение временных задержек
Конденсатор, подключённый к источнику постоянного тока, заряжается с постоянной скоростью. Такая схема является основой генераторов линейно меняющегося напряжения и пилообразного сигнала, используемых в аналоговых генераторах функций, схемах развёртки осциллографов, аналого-цифровых преобразователях и времязадающих схемах. RC цепи используют для формирования импульсов ( моностабильный мультивибратор ). Все эти задачи очень важны и используются в электронике повсеместно. Они рассматриваются в Частях _2 , _3 , _6 , _7 , 10 и 13 .
1.7.17 Обобщение теоремы Тевенина
Если схема содержит конденсаторы и индуктивности, то теорему Тевенина нужно переопределять. Любая двухвыводная цепь, содержащая резисторы, конденсаторы, катушки и источники сигналов может быть заменена эквивалентной схемой из одного комплексного импеданса последовательно с источником сигнала. Как и ранее, комплексный импеданс и источник сигнала с некоторой амплитудой, фазой и формой находятся по выходному напряжению на разомкнутых концах схемы и току короткого замыкания.
==55
42 Проверять предельные значения всегда полезно. В данном случае мы видим, что для большой величины ёмкости \( P→V^2/R\) , а для малой - \(|I|→V_0/X_C\) или \( V_0ω C\) , таким образом, \( P→I^2R=V_0^2ω ^2C^2R\) соответствует обоим ограничениям. <-
43 Или для нелинейных устройств коэффициент мощности показывает, что форма тока не пропорциональна форме напряжения. Вопрос разбирается в §9.7.1 . <-
44 При упоминании частоты «-3dB» знак минуса часто опускают. <-
45 Как указывалось в §1.7.1.A , удобно обозначить частоту среза \(ω_0=\frac{1}{RC}\) и работать с отношением \(ω/ω_0\) . В таком случае знаменатель в уравнении [1.36] принимает удобный вид \(\sqrt{1+(ω/ω_0 )^2}\). Аналогично можно упростить и уравнение [1.35] , где знаменатель превращается в \(ω/ω_0\) . <-
46 Или, эквивалентно, Q=\(R/X_C=R/X_L\) , где \(X_C=X_L\) - реактивные сопротивления на частоте \(ω_0\) . <-
47 В Части X1 рассказывается, в чём именно компоненты отличаются от идеала. Чаще всего речь идёт о действующем последовательном сопротивлении ESR . <-
48 Или, эквивалентно, Q=\(X_C/R=X_L/R\) , где \(X_C=X_L\) - реактивные сопротивления на частоте \(ω_0\) . <-

