1.4 Конденсаторы и схемы переменного тока
==18
Как только возникает слово изменение напряжения или тока, т.е. «сигнал», тут же обнаруживаются два очень интересных компонента, которые бесполезны на постоянном токе: конденсатор и катушка индуктивности. Эти простые устройства в связке с резистором образуют триаду пассивных компонентов, составляющих основу всех схем вообще 20 . Скажем, без конденсаторов не обходится ни одно устройство. Конденсаторы используются в генераторах и фильтрах, интеграторах и дифференциаторах. Они блокируют и шунтируют, а в паре с катушками позволяют строить фильтры, которые помогают выделить нужный сигнал из общего шума. Некоторые из примеров встретятся в этой части, а некоторые интересные варианты будут представлены позднее.
Начнём с рассмотрения конденсатора во всех подробностях. Часть обсуждения активно использует математический аппарат, и читатель может слегка освежить свои познания в этой области, ознакомившись с Приложением _A . В любом случае в долговременной перспективе понимание деталей не столь важно, как понимание результатов [* взаимоисключающие параграфы] .
1.4.1 Конденсаторы
Конденсатор ( рис. 1.27 ) - устройство, состоящее из двух проводников, изолированных друг от друга, обладающих следующим свойством:
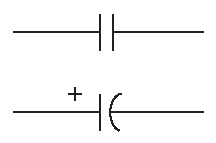
Рис. 1.27 Схемные изображения конденсаторов. Изогнутый электрод обозначает отрицательный вывод в поляризованных конденсаторах или внешнюю сторону фольги в рулонных металлоплёночных
\[ Q = CV. \qquad \qquad \qquad \qquad \quad [1.13] \]
В своей базовой форме конденсатор выглядит как две металлические поверхности, разделённые слоем изолирующего материала. В цилиндрическом конденсаторе с осевыми выводами такая трёхслойная конструкция скатана в рулон ( рис. 1.28 ). Конденсатор ёмкостью \( C \) фарад, имеющий напряжение между выводами \( V \) вольт, хранит заряд \(Q\) кулон на одной поверхности и \(–Q\) на другой. Ёмкость пропорциональна площади [* перекрытия] проводящих поверхностей и обратно пропорционально расстоянию между ними [*] . Для простой конструкции из параллельных пластин площадью A , разделённых зазором величиной d ( причём d≪A ) ёмкость равна \[ C=8.85×10^{-14}ε\frac{A}{d}, \quad \mathrm{Farad} \quad [1.14] \]
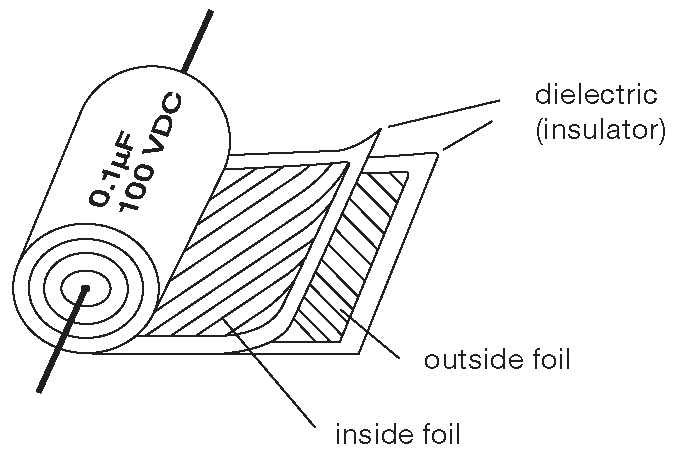
Рис. 1.28 Если раскрутить цилиндрический конденсатор, можно обнаружить длинную ленту металлизированной пластиковой плёнки
где ε - диэлектрическая постоянная, характеризующая изолятор, а размеры выражены в сантиметрах. Чтобы получить цифры, обычно встречающиеся на схемах, площадь должна быть большая, а зазор маленьким 21 . Например, пластины площадью 1cm2 , разделённые зазором 1 mm , будут иметь ёмкость чуть меньшую \(10^{-12}\) F ( пикофарада ). Понадобится 100'000 таких изделий, чтобы собрать один конденсатор на 0.1 μF , который не представляет собой ничего особенного: при разработке постоянно мелькают цифры в сотни микрофарад. В обычной ситуации считать ёмкость не требуется, т.к. конденсаторы можно приобрести, как стандартный компонент [* и со стандартным набором номиналов, см. §С.2 ] .
[*]
[* Исходя из того, что «ёмкость пропорциональна площади перекрывающихся проводящих поверхностей и обратно пропорционально расстоянию между ними», a «ε» всего-навсего постоянный корректирующий коэффициент, можно с уверенностью утверждать, что ёмкость имеет размерность cm2/cm = cm , т.е. даже не площади, а длины. Вот так номер ! Кстати, в физической системе СГС она сантиметрами и меряется. ]
==19
В первом приближении конденсаторы можно рассматривать в качестве частотно-зависимых резисторов. Они позволяют создавать частотно-зависимые делители напряжения. В некоторых случаях (шунтирование или разделение цепей ) это всё, что надо знать. В других ситуациях ( фильтры, накопление энергии, резонансные цепи ) требуются более глубокие знания. Например, идеальный конденсатор не рассеивает энергию, даже если через него течёт ток, потому что ток и напряжение различаются по фазе на 90° .
Перед погружением в тему специфических особенностей конденсаторов ( включающих некоторые математические выкладки для изменения параметров по времени и частоте ), будет полезно разобрать два первых направления использования - шунтирование и разделение, потому что в этих задачах конденсаторы используются чаще всего, и этот режим проще понять. Тема подробно разбирается в §1.7.1.C и §1.7.16.A , но ждать так долго совсем не обязательно: всё достаточно очевидно. На постоянном токе конденсатор выглядит как разрыв, поэтому он позволяет передать меняющийся сигнал, но блокирует его среднюю постоянную составляющую. Это разделительный ( блокирующий ) конденсатор, который используется для связи по переменному току , см. рис. 1.93 . Он может давить ( «шунтировать» ) сигнал там, где это требуется, так как выглядит как коротко замкнутая цепь на высокой частоте. Например, на рис. 8.80A конденсаторы давят сигналы в шинах +5VQ , –5VQ и на выводе базы транзистора \(Q_2\) 22 . С точки зрения общего числа конденсаторов в мире это два самых массовых сегмента их применения.
Если взять производную по времени из уравнения [1.13] , получим
\[ I=C\frac{dV}{dt}. \qquad \qquad [1.15] \]
Т.е конденсатор сложнее, чем резистор. Ток пропорционален не напряжению, но скорости его изменения. Если на выводах конденсатора ёмкостью 1 фарада менять напряжение со скоростью 1 вольт в секунду, то в цепи будет течь ток 1 ампер. Верно и обратное. Если задать ток 1 ампер, то напряжение будет меняться со скоростью 1 вольт в секунду. Фарада - очень большая ёмкость. Обычно работать приходится с микрофарадами ( 1 μF=\(10^{-6}\) F ), нанофарадами ( 1 nF=\(10^{-9}\) F и пикофарадами ( 1 pF=\(10^{-12}\) F ) 23 . Например, если задать ток 1 mA в 1 μF , то напряжение будет расти со скоростью 1000 V/s . Импульс такого тока длительностью 10 ms изменит напряжение на конденсаторе на 10 V ( рис. 1.29 ).
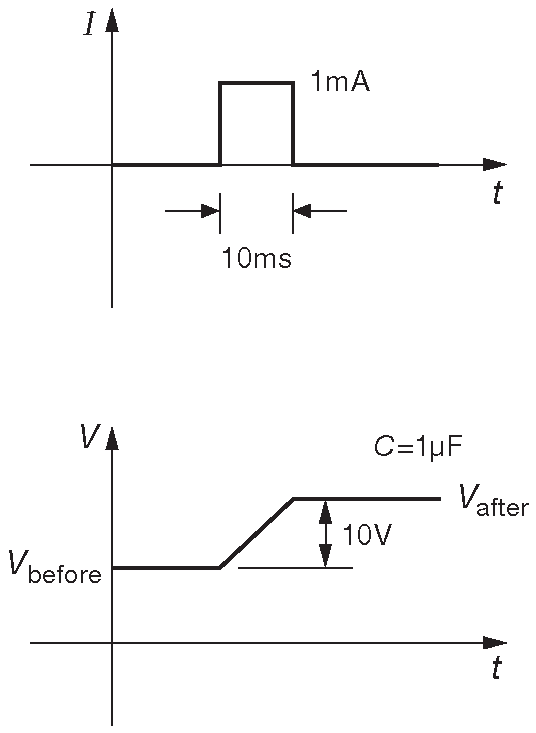
Рис. 1.29 Напряжение на конденсаторе меняется, когда через него течёт ток
При заряде конденсатора тратится энергия. Конденсатор не нагревается, потому что энергия накапливается в электрическом поле между обкладками. Можете проверить себя и подсчитать её. Результат \[ U_C=\frac{1}{2}CV^2, \qquad \qquad [1.16] \]
где \(U_C\) выражается в джоулях, \( C \) в фарадах, \( V \) - в вольтах. Это важный результат. Он понадобится чуть позже.
Упражнение 1.14
Проведите небольшие изыскания. Вообразим, что конденсатор ёмкостью \( C \) заряжается от 0V до напряжения \( V_f\) . Если выписывать формулы правильно, то станет видно, что результат не зависит от профиля заряда, т.е. не нужно удерживать ток на постоянном уровне ( но это, естественно, не возбраняется ). При любом мгновенном значении поток энергии в конденсатор равен (\( V · I\)) J/s ( джоулей в секунду ). Останется проинтегрировать \( dU=( V·I )dt\) от 0 до \( V_f\) . Это и будет ответ.
==20
Конденсаторы выпускаются в самых невероятных исполнениях и размерах. Некоторое представление можно получить по рис. 1.30 . Самые маленькие ёмкости можно встретить у трубчатых конденсаторов или у моделей базовой конструкции - металлизированной керамической пластины. Для больших емкостей требуется больше площади и меньший зазор между обкладками. Стандартным решением является изолирующий материал ( диэлектрик ) с проводящим покрытием с обеих сторон. В таком качестве может выступать алитированная ( покрытая алюминием ) пластиковая плёнка, скатанная в рулон. Другими распространёнными конструкциями являются: слоёная керамическая ( чип-конденсаторы ), оксидированная металлическая плёнка ( электролитические конденсаторы ) и металлизированная слюда. Каждый вид имеет свои уникальные свойства, краткий обзор которых даётся в Части X1 [* ##§X1.3 ] . В общем случае керамические и полиэстеровые используют в большинстве некритичных задач. Поликарбонат, полистирол, полипропилен, тефлон или стекло ставят в места с повышенными требованиями к параметрам. Танталовые берут, если нужна большая ёмкость, а алюминиевые служат развязкой по питанию.

Рис. 1.30 Конденсаторы способны принимать самое необычное обличие, вот неплохая выборка. Внизу слева лежат небольшие подстроечные конденсаторы ( один воздушный, три керамических ). Над ними поляризованные алюминиевые электролитические ( три слева имеют выводы на одну сторону - радиальные , три справа с выводами на обе стороны - аксиальные ). Слева вверху вариант с винтовым креплением. Дальше в верхнем ряду металлоплёночный низкоиндуктивный ( обратите внимание на широкие плоские выводы ), бумажный маслонаполненный и три дисковых керамических конденсатора один под другим. Ниже четыре прямоугольных металлоплёночных ( полиэстер, поликарбонат или полипропилен ). Соединитель D-типа смотрится чужеродно, но на самом деле имеет встроенные конденсаторы 1000 pF с каждого вывода на корпус. Слева от него группа из семи поляризованных танталовых электролитических ( пять с аксиальными выводами, один с радиальными и один для поверхностного монтажа ). Над ними три металлоплёночных с аксиальными выводами. Десять корпусов в центре снизу - керамические ( четыре радиальных, два аксиальных и четыре чип-конденсатора для поверхностного монтажа ). Над ними два высоковольтных ( аксиальный стеклянный и керамический под винтовое крепление ). Наконец, ниже левее центра четыре слюдяных радиальных и два похожих на диоды объекта - варакторы . Это конденсаторы, управляемые напряжением, и в самом деле сделанные на основе p-n перехода
==21
1.4.1.A Параллельное и последовательное соединение конденсаторов
Ёмкость нескольких конденсаторов, включённых параллельно, равна сумме их емкостей. Это легко показать. Подадим напряжение на параллельную комбинацию: \[ \begin {align} C_{total}V = Q_{total} &= Q_1 + Q_2 + Q_3 +... \\ &= C_1V + C_2V + C_3V + ... \\ &= ( C_1 + C_2 + C_3 + ... )V \end {align} \] или \[ C_{total} = C_1 + C_2 + C_3 +... \qquad [1.17] \]
Для последовательного соединения формула напоминает параллельное соединение резисторов: \[ C_{total} = \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+} \quad \qquad [1.18] \] или для двух конденсаторов: \[ C_{total} = \frac{C_1C_2}{C_1+C_2} \]
Упражнение 1.15
Покажите вывод формулы для двух последовательных конденсаторов.
Подсказка : точка соединения двух конденсаторов - внутренняя и не имеет внешних соединений, следовательно, заряды конденсаторов равны.
Ток, текущий через конденсатор в процессе зарядки ( \(I=C( dV/dt )\) ), не похож на ток через резистор: он пропорционален не напряжению, а скорости его изменения ( производной для напряжения по времени ). Более того, мощность ( \( V · I\) ), требуемая для заряда конденсатора не превращается в тепло, а запасается внутри в виде энергии электрического поля между обкладками. Эту энергию можно получить обратно, разряжая конденсатор. Эти особенности можно рассматривать и с другой стороны, что и будет сделано в §1.7 в ходе знакомства с реактивностью .
1.4.2 RC цепи: напряжение и ток во времени
При обсуждении цепей переменного тока или в общем случае любой схемы, в которой меняются напряжения и токи, можно использовать два подхода. Можно говорить об изменении напряжения и тока во времени или о зависимости амплитуды от частоты. Каждый из подходов имеет свои достоинства, и оба допускают лёгкое переключение с одного формата на другой в зависимости от удобства представления в конкретной ситуации. Изучение начнётся во временнОй области , а, начиная с §1.7 , перейдёт в частотную область .
Что интересного в цепях с конденсаторами? Чтобы ответить на вопрос рассмотрим простую RC цепь ( рис. 1.31 ). Уравнение для тока конденсатора позволяет написать
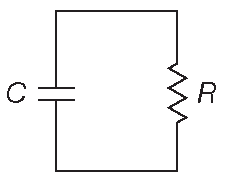
Рис. 1.31 Самая простая RC цепь
\[ C\frac{dV}{dt}=I=\frac{V}{R}. \qquad [1.19] \]
Это, если кто не знает, дифференциальное уравнение. Его решение:
\[ V = A×\exp{\Big[-\frac{t}{RC}\Big]}. \qquad [1.20] \]
Т.е. заряженный конденсатор, поставленный в схему 1.31 , будет разряжаться в соответствии с графиком 1.32 . Ток в схеме определяется уравнением для резистора и пропорционален остающемуся на конденсаторе напряжению, но скорость разряда ( наклон графика ) определяется уравнением для конденсатора и пропорциональна тому самому току. Поэтому разряд является функцией, чья производная пропорциональна значению функции, т.е. экспонента.
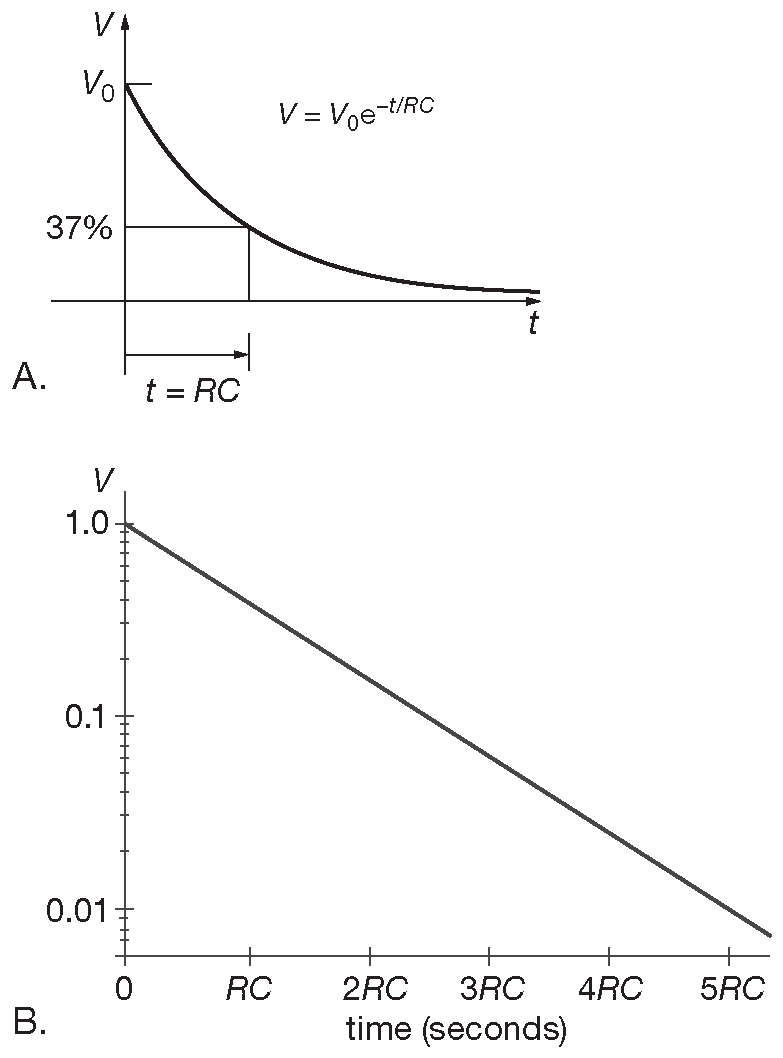
Рис. 1.32 Разряд RC цепи в линейных (A) и логарифмических (B) координатах
==22
1.4.2.A Постоянная времени
Произведение \(R ×C\) называют постоянной времени схемы. Для \(R\) в омах и \( C \) в фарадах \(R ×C\) выражается в секундах. 1 μF и 1 kΩ дадут 1 ms . Если на конденсатор подать 1V , то начальный ток будет 1 mA .
На рис. 1.33 показана чуть иная схема. В момент времени t=0 ключ подключает батарею. Сигналы в схеме описываются уравнением:
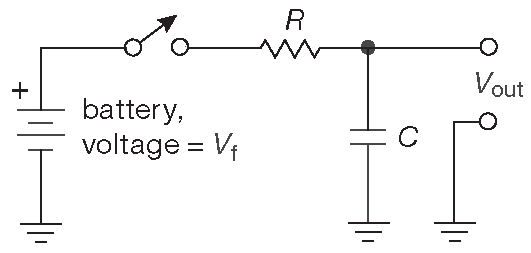
Рис. 1.33 Заряжаемая RC цепь
\[ I=C\frac{dV}{dt}=\frac{V_f-V_{out}}{R}. \]
Очередное дифференциальное уравнение. Его решение \[ V_{out} = V_f + Ae^{[-t/( RC )]}. \]
(Если математика непонятна, не отчаивайтесь. На данном этапе важно запомнить решение и важные выводы. Дальше этот результат будет часто использоваться. Для чуть заржавевшей математики может быть полезен краткий обзор в Приложении _A ). Константа A обуславливается начальными условиями. Для рис. 1.34 в момент t=0 имеем \( V \)=0 , следовательно, A=\(-V_f\) и \[ V_{out}=V_f\left(1-e^{[-t/( RC )]}\right ). \qquad [1.21] \]
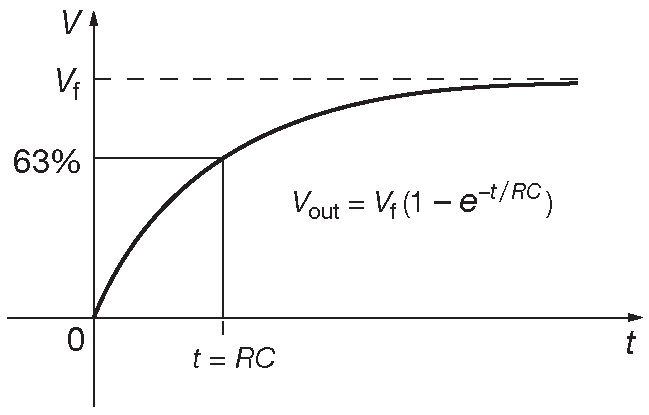
Рис. 1.34 График заряда RC цепи
Наклон графика зарядки конденсатора ( пропорциональный току ) пропорционален разнице между напряжением батареи и напряжением на конденсаторе, потому что именно это напряжение прикладывается к резистору, который и задаёт ток. В итоге получаем кривую, чей угол наклона уменьшается вместе с дистанцией до уровня зарядки. Опять экспонента.
Можно поработать с последней формулой и получить время, нужное, чтобы достичь напряжения \( V \) на пути к итоговому потенциалу \( V_f\) . Вся нужная для этого математика есть в Приложении _A . Результатом должно стать \[ t=RC\ln\left(\frac{V_f}{V_f-V}\right ) \qquad [1.22] \]
1.4.2.B Разряд до точки равновесия
Рано или поздно \( V \) достигнет уровня \( V_f\) ( t ≫ RC ). Есть «правило 5RC»: конденсатор заряжается или разряжается на 99% за время пяти постоянных времени. Если напряжение батареи изменится до какого-либо иного значения, например 0V , выходное напряжение начнёт переход к нему по такой же экспоненте \(e^{-t/( RC )}\) . На рис. 1.35 показано, что будет на выходе, если вместо батареи на вход подать прямоугольный сигнал \( V_{in}( t )\) .
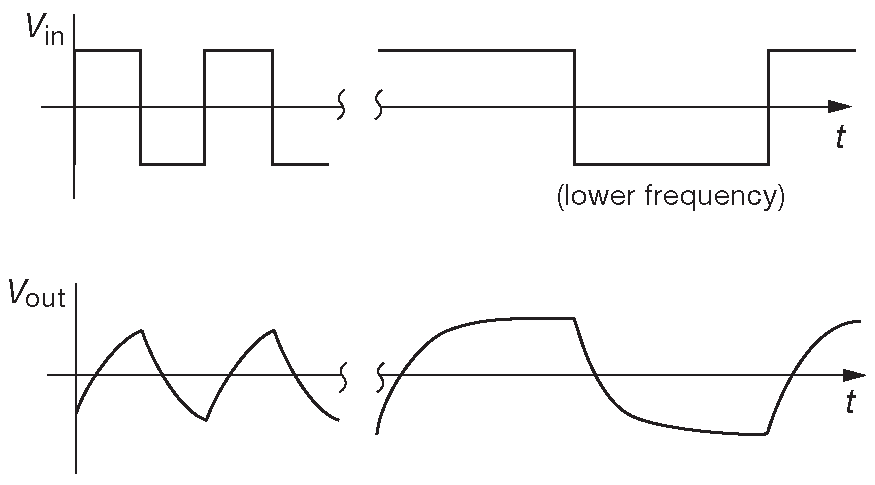
Рис. 1.35 Форма сигнала на входе схемы 1.33 и на её выходе
Упражнение 1.16
Покажите, что время роста выходного сигнала от 10% до 90% итоговой величины составит 2.2RC .
Возникает следующий очевидный вопрос: как выглядит напряжение \( V( t )\) для случайного \( V_{in}( t )\) ? Оно описывается неоднородным дифференциальным уравнением, которое решается стандартными методами. Сам вывод выходит за рамки книги, но результатом будет \[ V( t )=\frac{1}{RC}\int_{- ∞ }^tV_{in}( τ )e^{[-{( t-τ)}/{( RC )}]}\space dτ \]
Получается, что RC цепь усредняет предшествующие события на входе с взвешивающим коэффициентом \[ e^{[-{ Δ t}/{( RC )}]}. \]
На практике такие вопросы возникают редко. Вместо подобных расчётов просто переходят в частотную область , где речь идёт о том, сколько из имеющихся в сигнале частотных компонент пройдёт на выход. Эта важная тема будет разбираться в §1.7 , а до неё есть несколько других интересных схем, которые несложно анализировать во временной области.
==23
1.4.2.C Упрощение с помощью преобразования Тевенина
Можно двигаться дальше по этому пути и разбирать более сложные схемы, выписывая для них дифференциальные уравнения с последующим их разоблачением. Но в большинстве случаев это не самый продуктивный путь, т.к. результат будет очень похож на тот, который уже получен для простой RC цепи. Многие схемы можно сразу свести к ней. Например, для схемы на рис. 1.36 , чтобы получить параметры выходного сигнала \( V( t )\) для входного перепада \( V_{in}( t )\) , надо провести преобразование Тевенина для входного делителя \(R_1R_2\) .
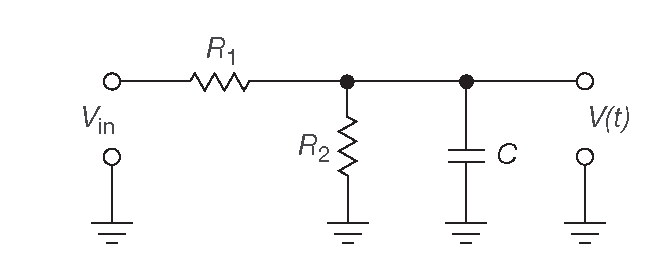
Рис. 1.36 Схема выглядит сложной, но это обманчивое впечатление ( Тевенин вам в помощь )
Упражнение 1.17
Для схемы 1.36 : \(R_1=R_2\)=10 kΩ , \( C \)=0.1 μF . Найдите \( V( t )\) и нарисуйте график.
1.4.2.D Пример: схема задержки
Отвлечёмся от теоретических штудий и разберём несколько реальных схем. Учебники часто избегают такого прагматичного подхода, особенно на ранних этапах, но авторы считают, что интереснее всего изучать электронику на практических примерах. Для этой задачи потребуются несколько «чёрных ящиков», с помощью которых можно будет строить схемы. Позднее, в других частях книги будет разобрано устройство самих «ящиков».
Ранее уже шла речь о логических уровнях - напряжениях в логических схемах. На рис. 1.37 показано, как сделать на конденсаторе задержку для импульса. Треугольники на схеме - символ КМОП буферов 24 . Они выдают на выходе сигнал ВЫСОКОГО уровня [* уровень положительного питания] для ВЫСОКОГО уровня на входе ( т.е. потенциал, напряжение которого выше половины питающего напряжения ) и НИЗКОГО уровня [* уровень земли ] для НИЗКОГО уровня на входе. Первый буфер создаёт копию входного сигнала и защищает источник сигнала от нагрузки, создаваемой RC цепью ( этот вопрос разбирался в §1.2.5.A ). На графике выходного напряжения RC цепи присутствуют характерные участки экспоненциального заряда-разряда, которые заставляют выходной буфер переключаться на 10 μs позднее перепада на входе ( сигнал RC цепи достигает уровня 50% за время t=0.7RC ). В реальной схеме надо также учитывать эффекты отклонения пороговых уровней от средней точки питания, т.к. они приведут к изменению длительности задержки и ширины импульса. Подобные схемы применяются там, где надо задержать импульс до появления какого-либо события. При разработке следует избегать таких приёмов, но иногда они могут сильно помочь.
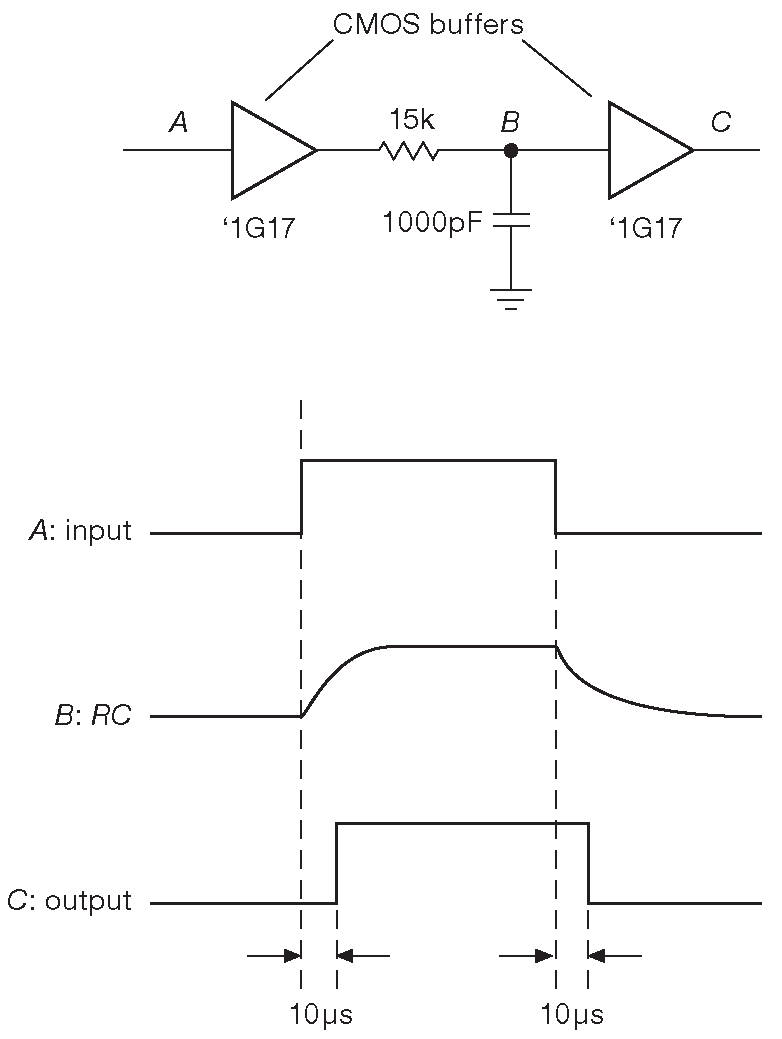
Рис. 1.37 Задержка цифрового сигнала с помощью RC цепочки и пары буферов из семейства LVC’ ( это маленькие одновентильные микросхемы с очень длинным полным обозначением - SN74LVC1G17DCKR. Во! )
1.4.2.E Другой пример: «Питание на одну минуту»
На рис. 1.38 показан другой пример применения RC цепочки - «Питание на одну минуту» . Треугольный символ на схеме - компаратор [* который уже встречался в схеме 1.18 ] . Подробный разбор отложен до Части _4 и Части 12 , а сейчас про него надо знать следующее.
- Это микросхема ( набор резисторов и транзисторов в общем корпусе ).
- Он питается от положительного источника, подключённого к выводу «V+».
- Он выдаёт на выход ( справа ) напряжение V+ или землю. Уровень зависит от уровня на входе (+) относительно входа (–). Если (+) более положителен, чем (–), то на выходе V+ , если более отрицателен, то земля.
Выходы называются неинвертирующий и инвертирующий соответственно. Компаратор не потребляет ток по входам и спокойно тянет нагрузку 20 mA и более, а на выходе может быть только два состояния: ВЫСОКОЕ ( V+ ) и НИЗКОЕ ( земля ).
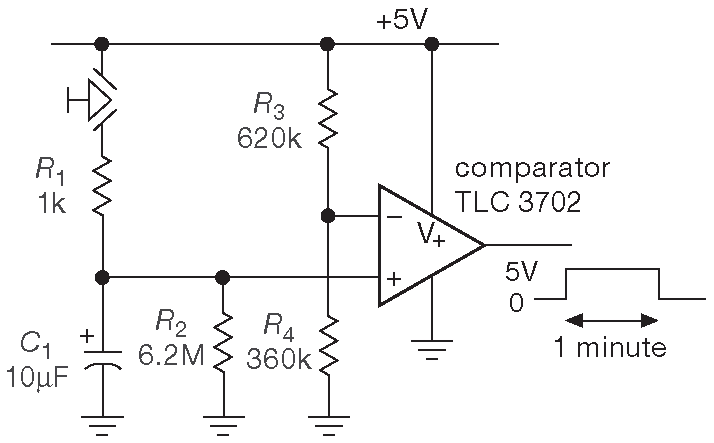
Рис. 1.38 Использование постоянной времени RC для отсчёта времени: одно нажатие - одна минута
==24
Вот как работает схема. Делитель напряжения \(R_3R_4\) удерживает вход (-) на уровне 37% от напряжения питания. В данном случае это +1.8 V . Назовём его «опорное напряжение». Пока в схеме ничего не происходит, \( C_1 \) полностью разряжен, и выход компаратора сидит на земле. Если кратковременно нажать на кнопку «START», \( C_1 \) зарядится ( с постоянной времени 10 ms , т.е. достаточно быстро ) до +5V . Такое напряжение на входе (+) заставит компаратор переключить выход на V+ ( т.е. те же +5V ), см. рис. 1.39 . После отпускания кнопки конденсатор начинает разряжаться по экспоненте до уровня земли. Постоянная времени \(τ=R_2C_1\) устанавливает задержку 1 минута. Когда напряжение на конденсаторе пересечёт опорный уровень, компаратор выдаст на выход уровень земли. Отметим, что для удобства опорный уровень выбран так ( V+/\(e\) ), чтобы задержка в точности равнялась постоянной времени \(τ\) . Для \(R_2\) выбрано ближайшее к 6 MΩ значение из стандартного ряда, см. Приложение _C . В итоге после нажатия на кнопку на выходе на 1 минуту появляется ВЫСОКИЙ ( +5V ) уровень.
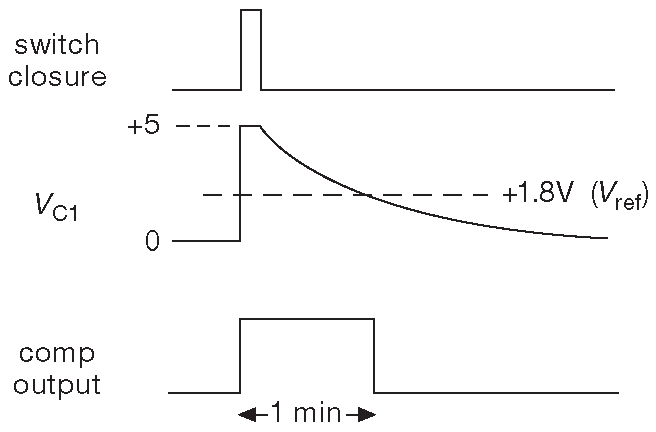
Рис. 1.39 Временная диаграмма сигналов в схеме 1.38 . Напряжение \( V_{C1}\) возрастает до +5V за время \(R_1C_1\)≈10 ms
На выход можно подключить полезную нагрузку. Как это делается, показывает рис. 1.40 . Можно сделать брелок-индикатор для ключей с автоматическим выключением. Для этого надо подключить на выход светодиод через последовательный резистор. Если хочется пошуметь немного, можно повесить на выход пьезоизлучатель , который будет подавать сигнал в течение одной минуты, например, так можно сделать сигнал окончания стирки. Можно задействовать небольшое электромеханическое реле , которое является простым переключателем с электрическим управлением. Реле имеет пару контактов и может управлять через них какой-нибудь нагрузкой. Использование реле имеет одно важное свойство - нагрузка электрически изолирована от управляющей схемы.
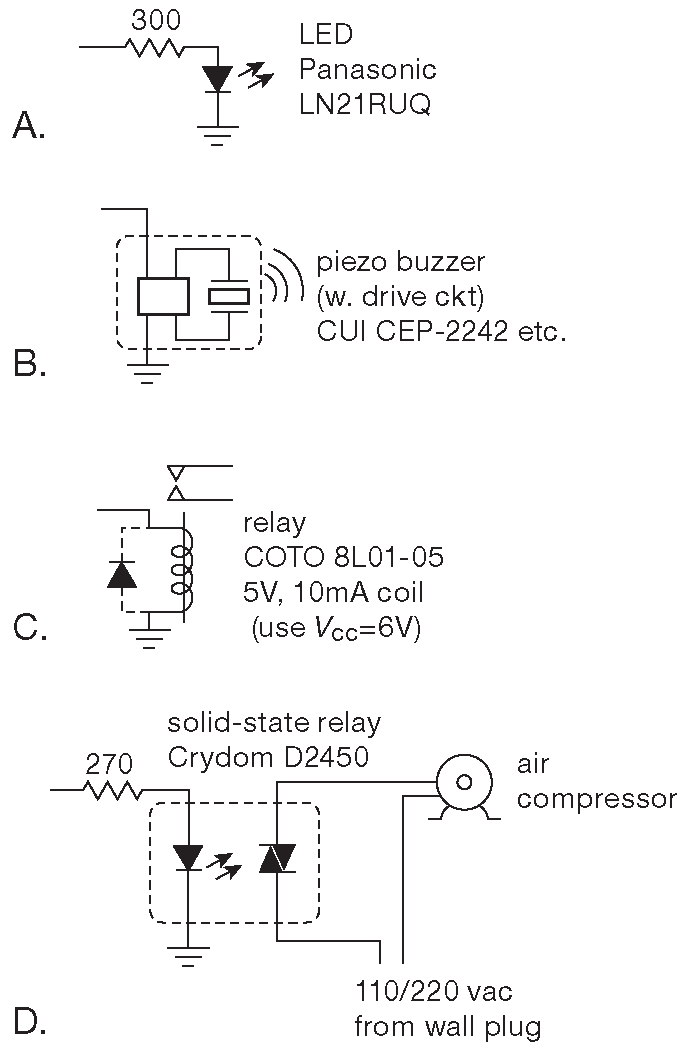
Рис. 1.40 Подключение полезной нагрузки к выходу схемы 1.38
Наконец, если требуется включать какое-то серьёзное оборудование, можно использовать мощное твердотельное реле ( SSR , §12.7 ), в котором инфракрасный диод управляет симистором . При включении тиристор работает как отличный механический ключ, способный коммутировать токи величиной многие амперы и, подобно механическому реле, изолирует нагрузку от управляющей схемы. На картинке показан воздушный компрессор, которым в течение одной минуты можно накачивать воздухом колёса в домашней «заправке». То же можно делать и с воздушной сушилкой, причём время не обязательно ограничивать одной минутой.
==25
Некоторые детали.
- В схеме 1.38 можно исключить \(R_1\) . Схема будет работать, но при подключении разряженного конденсатора к шине +5V в первое мгновение будет возникать большой бросок тока. Здесь полезно вспомнить, что \(I=C( dV/dt )\) , причём «\( dV\)» эквивалентно +5V , а «\( dt\)» - практически нулю. [* Авторы провели неявное преобразование типов, превратив \( dV\) в \(ΔV\) , а \( dt\) в \(Δt\) , что в общем случае некорректно и подходит только для случаев малых приращений аргумента, т.е. когда \(Δt→0\) . ] Последовательный резистор \(R_1\) ограничивает ток в такой ситуации до незначительных 5 mA , но позволяет конденсатору зарядиться достаточно быстро ( >99% для 5RC составит ∼0.05 s ).
- Выход компаратора будет не сразу переключаться из одного состояния в другое, но прыгать туда-сюда некоторое время ( см. рис. 4.31 ). Это происходит из-за слишком плавного изменения напряжения на входе «+», что позволяет внешнему шуму влиять на результаты сравнения \( V_{C1}\) и опорного уровня. Проблема решается с помощью дополнительных компонентов, возвращающих часть выходного напряжения обратно на вход, чтобы ускорить переключение ( схема носит официальное название гистерезис или положительная обратная связь , она встретится в Части _2 и _4 ). [* Вернее гистерезис является свойством схемы с положительной обратной связью] .
- В электронных схемах надо в обязательном порядке ставить развязочные конденсаторы между шинами питания и земли. Величина ёмкости не критична: подойдёт любое значение от 0.1 μF до 10 μF , см. §1.7.16.A .
Этот простой пример предполагается использовать для включения и выключения нагрузки, но для логического выхода компаратора ( имеющего только два состояния ВЫСОКОЕ и НИЗКОЕ, 0 и 1 , ИСТИНА и ЛОЖЬ) бывают и иные применения. Например, такой сигнал может разрешать или запрещать работу другого устройства. Скажем, открытие двери может включать на 1 минуту клавиатуру на панели, которая позволит ввести кодовое слово, чтобы запустить двигатель. По истечении минуты, если код не набран, клавиатура блокируется, обеспечивая минимальный тест на трезвость.
1.4.3 Дифференциаторы
Можно собрать простую схему, которая будет дифференцировать входной сигнал, т.е. обеспечивать выполнение соотношения \( V_{out} ∝ dV_{in}/dt\) . Разберём, что происходит, последовательно.
- Сначала непрактичная схема 1.41A . Входное напряжение \( V_{in}( t )\) создаёт в конденсаторе ток \(I_{cap}=C( dV_{in}/dt )\) . Это именно то, что нужно, если бы удалось использовать этот ток. Но это невозможно 25 .
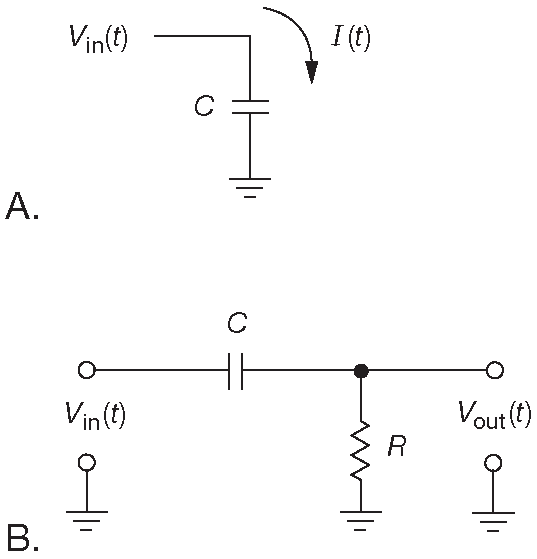
Рис. 1.41 Дифференциаторы. (A) Идеальный ( если не считать отсутствующего выхода. (B) Некоторое приближение к идеалу ( но здесь хотя бы выход есть! )
- Тогда добавим небольшой резистор между конденсатором и землёй, который будет работать «токочувствительным» шунтом ( рис. 1.41B ). Выход теперь пропорционален току через конденсатор, но сам ток более не пропорционален входному напряжению. Устройство перестало быть идеальным математическим дифференциатором. Это получается, потому что напряжение на обкладках, производная которого создаёт зарядный ток, наблюдаемый с помощью резистора, больше не эквивалентно \( V_{in}\) . Теперь это разница между \( V_{in}\) и \( V_{out}\) . Тогда: \[ I=C\frac{d}{dt}( V_{in}-V_{out})=\frac{V_{out}}{R}. \] Если выбрать R и C достаточно малыми, чтобы \[ \frac{dV_{out}}{dt} ≪ \frac{dV_{in}}{dt}, \] тогда: \[ C\frac{dV_{in}}{dt} ≈ \frac{V_{out}}{R} \] или \[ V_{out}( t ) ≈ RC \frac{d}{dt}V_{in}( t ). \] Т.е. получили выходной сигнал, пропорциональный скорости изменения входного напряжения.
Чтобы выполнить условие \( dV_{out}/dt ≪ dV_{in}/dt \) , произведение \(R · C\) приходится делать малым, причём величину \(R\) нельзя делать слишком малой, дабы не нагружать источник. ( В момент прохождения фронта входного сигнала напряжение между обкладками конденсатора не меняется [* не успевает: конденсатор не допускает мгновенного изменения напряжения между обкладками ] , что значит, источник сигнала видит нагрузку величиной \(R\) ). При рассмотрении этой схемы в частотной области ( §1.7.10 ) станут видны и другие подробности. Если подать на схему 1.41B прямоугольные импульсы, то выход будет выглядеть как на рис. 1.42 .
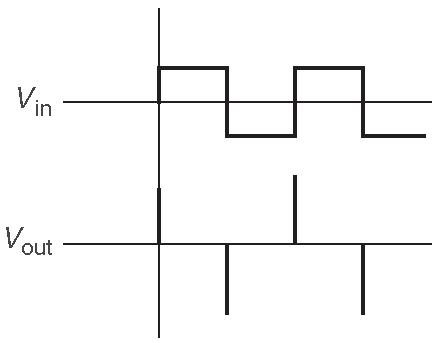
Рис. 1.42 Сигнал с дифференциатора ( снизу ), на который подан прямоугольный сигнал
Дифференциаторами удобно обнаруживать фронты импульсных сигналов, и в цифровых схемах иногда можно встретить что-либо подобное схеме 1.43 . RC дифференциатор создаёт выбросы на фронтах входного сигнала, а выходной буфер преобразует выброс в короткий импульс правильной формы. На входе внутри буфера стоит защитный диод, поэтому выброс в отрицательную область мал ( §1.6 ).
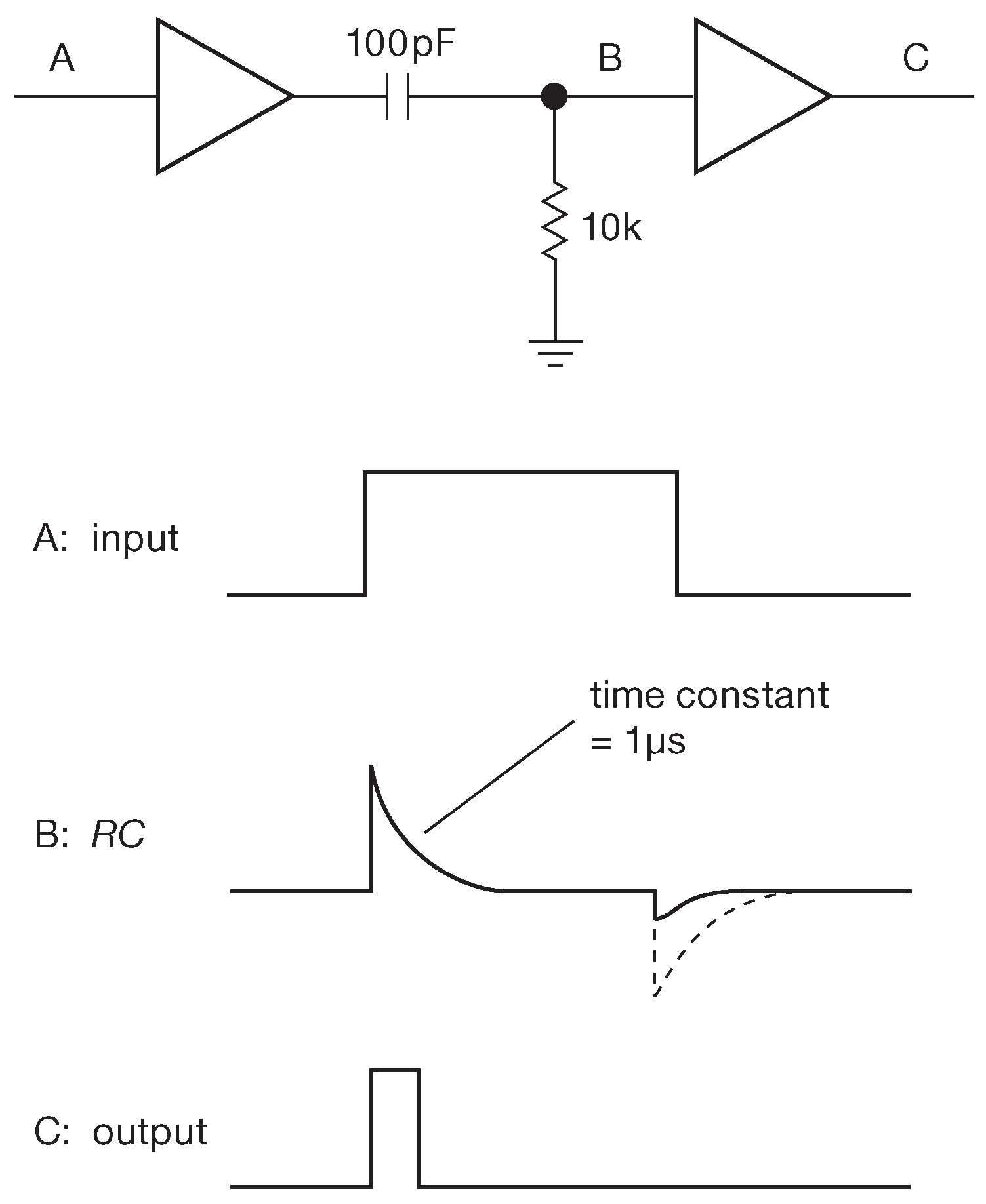
Рис. 1.43 Детектор возрастающего фронта
==26
Чтобы добавить теме толику реализма, были проведены измерения на реальной дифференцирующей цепочке. Номиналы рассчитаны на высокочастотные сигналы: \( C \)=1 pF и \(R\)=50 Ω ( резистор имеет стандартную для высокочастотных схем величину, см. Приложение _H ). Сигнал представлял собой ступеньку +5V с настраиваемой скоростью нарастания ( т.е. ( \( dV/dt\) ) ). Результаты показаны на рис. 1.44 . На таких скоростях ( по горизонтали 4 наносекунды на деление ) схемы часто отклоняются от идеального поведения, что заметно по сигналу с самым коротким фронтом. Две более пологих ступеньки выглядят правильнее: плоская вершина выходного импульса, тянущаяся, пока через дифференциатор проходит возрастающий фронт. [* Производная меняющегося линейно сигнала - константа ] . Проверьте корректность амплитуды по формуле.
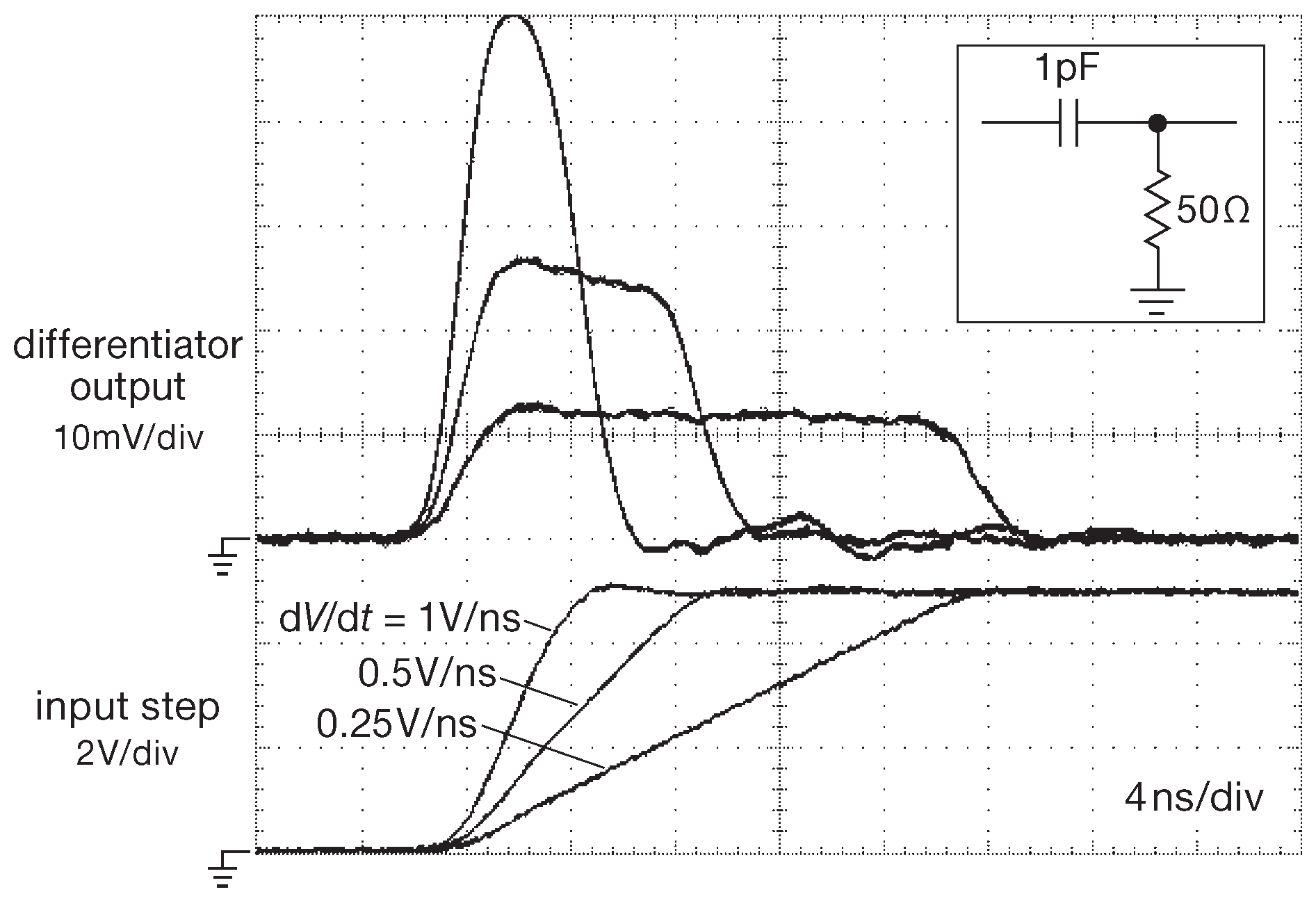
Рис. 1.44 Три перепада с различной скоростью нарастания, пропущенные через дифференцирующую RC цепочку, показанную на врезке. Для самого быстрого перехода ( \(10\space ^9\) вольт в секунду ) форма сигнала искажена несовершенством компонентов и ограничениями приборов
1.4.3.A Случайное возникновение дифференцирующих цепочек
Дифференциаторы иногда возникают там, где их никто не ждёт, и где они совсем не нужны. Иногда можно видеть картину, подобную изображённой на рис. 1.45 . В первом случае имеем дело с результатом наложения прямоугольного сигнала, наводящегося на интересующий узел через емкостную связь. Причиной может быть отсутствие согласования в наблюдаемой цепи. Если это не так, то можно попробовать уменьшить сопротивление источника, либо найти возможность снизить ёмкость связи с конфликтующим цифровым сигналом. Во втором случае наблюдаем прямоугольный сигнал с плохим контактом: плохо вставленный разъём или плохой контакт осциллографического пробника. Очень маленькая ёмкость такого разрыва в паре со входным сопротивлением прибора образуют дифференцирующую цепь. Понимание причин того, что схема «дифференцирует», позволяет найти и устранить проблему.
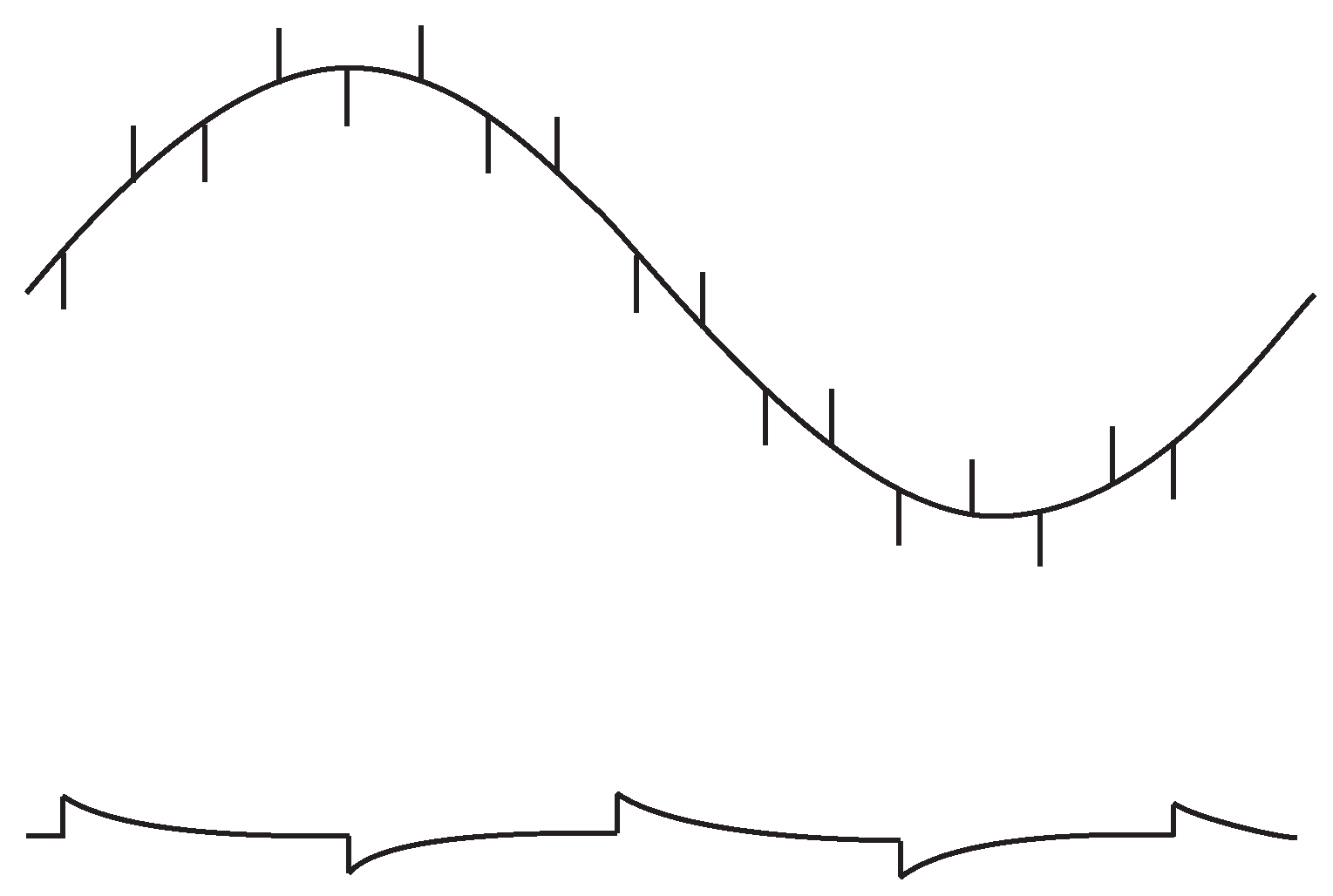
Рис. 1.45 Два примера работы нежелательных дифференцирующих цепей, возникающих при случайной емкостной связи
1.4.4 Интеграторы
Если RC цепи могут вычислять производные, то, может, и интеграл возьмут? Вновь применим двухшаговую схему.
- Вообразим, что есть входной сигнал в виде меняющегося по времени тока \(I_{in}( t )\) ( рис. 1.46A ) 26 . Этот ток в точности равен току через конденсатор. Тогда \(I_{in}( t )=C( dV/dt )\) и \( CV( t )=\int I_{in}( t )dt\) . Это именно то, что требуется. Иначе говоря, обычный конденсатор с одной заземлённой обкладкой является интегратором, если на входе токовый сигнал \(I_{in}\) . Но в большинстве случаев это не так.
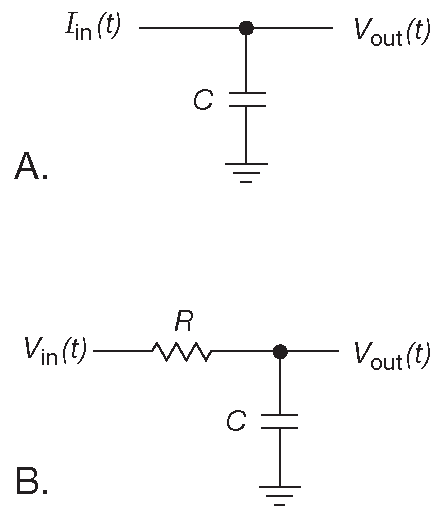
Рис. 1.46 Интегратор. (A) Идеальный, но требует токовый входной сигнал. (B) Приближение ( см. текст )
==27
- Тогда подключим на входе резистор и подадим на вход напряжение \( V_{in}( t )\) ( рис. 1.46B ). Такая схема работает, но перестаёт быть идеальным интегратором. Происходит это, потому что ток через конденсатор более не пропорционален входному сигналу \( V_{in}\) . Теперь он пропорционален разнице между \( V_{in}\) и \( V_{out}\) , т.е. имеем, напряжение на \(R\) равно ( \( V_{in}-V_{out}\) ) , значит \[ I=C\frac{dV}{dt}=\frac{V_{in}-V_{out}}{R}. \] Если выполняется условие \( V ≪ V_{in}\) , для чего произведение \(R · C\) должно быть большИм 27 , то \[ C\frac{dV}{dt} ≈ \frac{V_{in}}{R} \] или \[ V( t ) = \frac{1}{RC}\int_0^t V_{in}( t )dt + constant. \]
Получили выходной сигнал, пропорциональный интегралу входного сигнала по времени. [* Константа символизирует начальный заряд на конденсаторе ] . Как работает это приближение видно на прямоугольном входном сигнале ( рис. 1.37 ). В этом случае \( V( t )\) является экспоненциальной кривой заряда/разряда. Начальный участок экспоненты близок к линейному росту - интегралу от константы ( рис. 1.47 ). По мере увеличения произведения \(RC\) в работе оказывается всё меньшая часть экспоненты, которая всё ближе к идеальному линейному приближению.
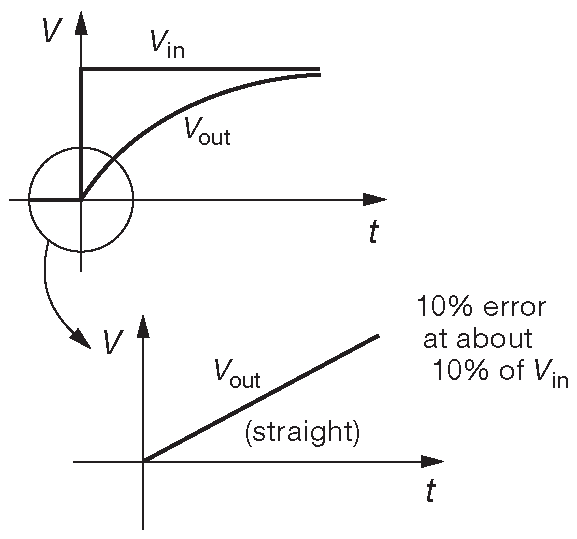
Рис. 1.47 Интегратор близок к идеальному, когда \( V_{out} ≪ V_{in}\)
Отметим, что условие \( V_{out} ≪ V_{in}\) аналогично требованию пропорциональности тока \(I\) и напряжения \( V_{in}\) , т.е. как в схеме интегратора. Большее напряжение, приложенное к большему сопротивлению, линеаризует ток и часто именно так и используется.
Позднее, при рассмотрении операционных усилителей и обратной связи, будет показан метод построения интеграторов, не имеющих ограничения \( V_{out} ≪ V_{in}\) . Такие схемы работают в большом диапазоне частот и входных напряжений с пренебрежимо малыми ошибками.
Интеграторы активно используются в аналоговой технике в качестве компонента для цепей управления, обратной связи, аналого-цифровых преобразователей и генераторов.
1.4.4.A Генератор линейно меняющегося напряжения
Теперь просто понять, как работает генератор линейно меняющегося напряжения. Это очень полезное устройство. Его используют во времязадающих цепях, схемах аналого-цифрового преобразования, генераторах функций и развёртках аналоговых осциллографов. Схема использует конденсатор, заряжаемый постоянным током ( рис. 1.48 ). Из уравнения работы конденсатора \(I=C( dV/dt )\) получается \( V( t )=(I/C )t\) . Выходное напряжение показано на рис. 1.49 . Линейный рост прекращается по достижении границы рабочего диапазона. На том же графике показано поведение простой RC цепи, для которой резистор подключён к источнику напряжения, равному по величине границе рабочего диапазона, а номинал выбран под начальный ток, равный току генератора линейного напряжения. Реальные источники тока имеют границы рабочего диапазона, определяемые возможностями собственного блока питания, поэтому данное сравнение вполне жизненно. В Части _2 , которая рассказывает о биполярных транзисторах, рассматриваются конструкции источников тока, которые будут модифицироваться и улучшаться в Части _3 ( полевые транзисторы ) и Части _4 ( операционные усилители ).
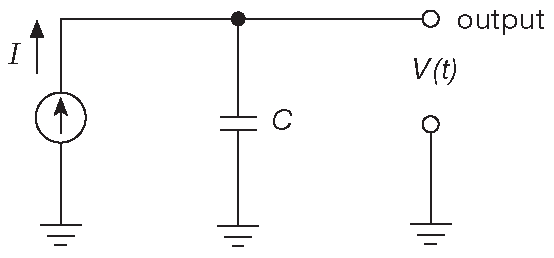
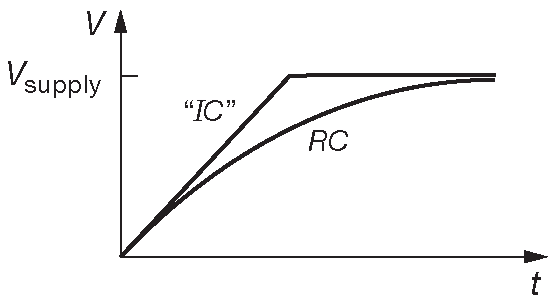
Рис. 1.48 Источник постоянного тока, заряжающий конденсатор, создаёт на нём напряжение, меняющееся с постоянной скоростью
Рис. 1.49 Зарядка от источника тока с ограниченным рабочим диапазоном в сравнении с зарядкой через резистор
Упражнение 1.18
Ток 1 mA заряжает конденсатор 1 μF . За какое время напряжение достигнет 10 V?
==28
1.4.5 Недостаточно идеальные конденсаторы
Реальные конденсаторы - те, что можно увидеть, потрогать, приобрести, ведут себя в соответствии с теорией, но имеют кое-какие дополнительные «особенности», которые создают проблемы в некоторых задачах. Например, у всех конденсаторов имеется последовательное сопротивление ( часто зависящее от частоты ) и последовательная индуктивность ( об индуктивностях рассказывает следующая глава ), и всё это в дополнение к частотно-зависимому параллельному сопротивлению. В них есть эффект «памяти» ( диэлектрическая абсорбция ), который редко упоминают воспитанные люди. Если конденсатор зарядить до напряжения \( V_0\) , подержать под этим потенциалом, а затем разрядить до 0V , то можно обнаружить, что после снятия короткого замыкания напряжение на конденсаторе начинает меняться в направлении \( V_0\) .
На данный момент эти эффекты не важны и будут обсуждаться наравне с другими особенностями в последующих частях и дополнительных темах Части X1 [* ##§X1.3 ] .
==28
20 Читатели научного журнала «Nature» ( London ) были встречены в 2008 году статьёй «Найден потерянный мемристор» (“The missing memristor found” ( D. B. Strukov et al., 453, 80, 2008 ), претендующей на обнаружение гипотетического «четвёртого фундаментального элемента» [пассивных схем]. Авторы скептически относятся к этой сенсации. Так или иначе, даже если полемика, в конечном счёте, завершится признанием данного факта, это не изменит нелинейного характера мемристора, а пассивных двухвыводных линейных двухвыводных элементов всего три. <-
21 Не стоит удивляться, что у них высокое значение диэлектрической константы: у воздуха ε=1 , плёночные имеют ε=2.1 ( полипропилен ) или 3.1 ( майлар ), а керамика и вовсе ε=45 ( C0G) или 3000 ( «X7R» ). <-
22 Ирония ситуации в том, что обязательные развязочные конденсаторы обязательны настолько, что обычно не указываются на принципиальных схемах ( это же правило действует в этой книге ). Не совершайте ошибки и не пропускайте их в реальных устройствах. <-
23 Чтобы больше запутать новичков на схемах обычно не ставят единицы измерения при номиналах. Предполагается, что они ясны из контекста. <-
24 Комплементарная металл-оксидная полупроводниковая технология ( КМОП ) - основной вид технологии для современных логических схем ( Часть 10 ). <-
25 Ценитель вспомнит возглас доктора Стренджелава: «Весь смысл машины возмездия теряется, если сохранять её существование в секрете! » <-
26 Сигналы рассматриваются как меняющееся по времени напряжение , но дальше будет показано, как можно преобразовать их в меняющиеся по времени токи . Для этих целей используют преобразователь напряжение-ток, они же «транскондуктивные усилители» [* они же источники тока, управляемые напряжением] . <-
27 Всё как в дифференциаторе. Другой взгляд на вопрос представлен в §1.7.10 . <-

