1.5 Катушки индуктивности и трансформаторы
==28
1.5.1 Катушки индуктивности
Если конденсаторы понятны, с катушками индуктивности ( рис. 1.50 ) трудностей не будет. Они очень похожи. Скорость изменения тока через индуктивность пропорциональна напряжению, приложенному к её концам ( в конденсаторе скорость изменения напряжения пропорциональна втекающему току ). Отсюда определение: \[ V=L\frac{dI}{dt}, \qquad [1.23] \]
Рис. 1.50 Схемный символ катушки индуктивности. Параллельные линии явно обозначают наличие сердечника из магнитного материала
где \(L\) - индуктивность, выражаемая в генри ( mH , μH , nH и т.д. ). Если приложить к выводам катушки индуктивности напряжение, ток в ней начнёт линейно возрастать ( сравните с конденсатором, в котором постоянный ток вызывает линейный рост напряжения ). 1 вольт, приложенный к 1 генри порождает ток, который возрастает на 1 ампер за 1 секунду.
Так же, как и в конденсаторе, энергия, потраченная на увеличение тока в катушке, сохраняется. Она накапливается в магнитном поле и выражается следующим соотношением \[ U_L = \frac{1}{2}LI^2, \qquad [1.24] \] где \(U_L\) в джоулях ( ватт-секунда ), \(L\) - в генри, \(I\) - в амперах. Это очень важное свойство, лежащее в основе преобразования мощности в источниках питания ( тех чёрных коробочках, которые вставляются в розетку и питают потребительскую электронику ). Об источниках питания рассказывается в Части _9 .
Символ катушки индуктивности похож на спираль из проволоки, каковая в самой простой форме и является катушкой индуктивности. Её несколько необычное поведение определяется магнитной природой, а именно: ток, текущий через катушку, создаёт магнитное поле выровненное по её оси, а изменение этого поля создаёт на концах катушки напряжение ( называемое «напряжение самоиндукции» ), которое пытается скомпенсировать изменение поля ( эффект описывается правилом Ленца ). Индуктивность \(L\) дросселя - просто отношение магнитного потока, проходящего через катушку, к току, создающему этот магнитный поток ( с учётом константы, задающей пропорцию ). Индуктивность зависит от геометрии катушки ( диаметра и длины ) и свойств магнитного материала сердечника, который может использоваться для усиления и сосредоточения магнитного поля. Индуктивность катушки заданной геометрии пропорциональна квадрату числа витков.
Упражнение 1.19
Объясните, почему \(L ∝\) n2 для дросселя, имеющего обмотку из n витков провода, если при изменении числа витков диаметр и длина самой катушки не меняется.
Некоторые подробности раскрываются в Части X1 [* ##§X1.4 ] , а здесь приводится эмпирическая оценочная формула индуктивности \(L\) для катушки диаметром d и длиной l , где зависимость от n2 выражена явно: \[ L ≈ k\frac{d^2n^2}{18d+40l} \space , \qquad \mathrm{ μ H} \] где k равно 1 для размеров в дюймах и 0.395 для сантиметров. Это формула Вилера . Её точность 1% для соотношения размеров l > 0.4d .
==29
Ток в катушке, подобно току в конденсаторе, имеет нелинейную зависимость от напряжения, чем отличается от тока в резисторе. Более того, мощность, связанная с током через катушку ( \( V ×I\) ), не превращается в тепло, но сохраняется в магнитном поле катушки. В конденсаторе мощность, связанная с током, также не рассеивается, а сохраняется в электрическом поле. Вся энергия может быть возвращена, если внешний ток через дроссель прекратится ( в конденсаторе напряжение между обкладками должно снизиться до нуля ).
Базовой конструкцией дросселя является катушка из проводника, которая может быть простым одиночным витком провода или сплошной намоткой, заполняющей некоторую длину, как в обмотке реле. Варианты включают намотку на сердечниках из различных материалов. Самые популярные - электротехническая сталь в виде пластин, ленты или порошка и феррит ( серый хрупкий непроводящий материал). За счёт «магнитной проницаемости» материала сердечник позволяет увеличить индуктивность обмотки. Выпускаются сердечники в виде цилиндров, катушек и колец, но встречаются и весьма замысловатые формы, например, чашки. Это пустотелый бублик из магнитного материала, разрезанный по плоскости на два кольца [* обмотка укладывается в канавку в одной половине и накрывается второй] . Некоторые дроссели можно посмотреть на рис. 1.51 .

Рис. 1.51 Дроссели с ферритовыми сердечниками. Верхний ряд слева направо : залитое кольцо, кольцо в герметичном исполнении, чашка для печатного монтажа, голое кольцо ( два размера ). Средний ряд : три подстроечные индуктивности с подвижным сердечником. Нижний ряд : сильноточный дроссель на ферритовом сердечнике, катушка на ферритовой «бусине», изолированная обливная катушка с радиальными выводами, два дросселя для поверхностного монтажа, изолированные катушки с аксиальными выводами ( два варианта ), лакированные катушки ( два вида )
Катушки индуктивности находят широкое применение в радиочастотных схемах ( RF ) в качестве отдельных компонентов или в виде элементов резонансных контуров ( §1.7.14 ). Пара близко расположенных катушек образуют интересный объект - трансформатор. Речь о нём чуть ниже.
Во многих своих проявлениях катушки индуктивности являются противоположностью конденсаторам 28 . Как они работают, будет объяснено позднее, когда будет разбираться понятие «импеданса».
1.5.1.A Заглядывая чуть вперёд: несколько фокусов с участием катушек
==30
Чтобы оценить, на что способны катушки индуктивности, взгляните на рис. 1.52 . Эти схемы подробно описываются в Части _9 , но, что в них происходит, можно понять с уже имеющимися знаниями. На рис. 1.52A левая половина дросселя \(L\) переключается между напряжением \( V_{in}\) и землёй на какой-то частоте, с равным промежутками временем для каждого состояния ( «50%-скважность» ). Но определение индуктивности \( V=L( dI/dt )\) требует, чтобы среднее напряжение на её выводах было равно нулю, в противном случае ток через катушку рос бы неограниченно. [* Уравнение говорит, что скорость изменения тока равна \( V \) , т.е., если \( V \) не равно нулю, то и скорость изменения тока ненулевая, и ток есть, и меняется] . Данное условие иногда называется правилом баланса произведения вольт-секунда . Из указанного условия следует, что среднее выходное напряжение должно равняться половине входного ( проверьте, что понимаете, почему это так ). В этой схеме \( C_2\) работает накопителем, усредняющим выходное напряжение.
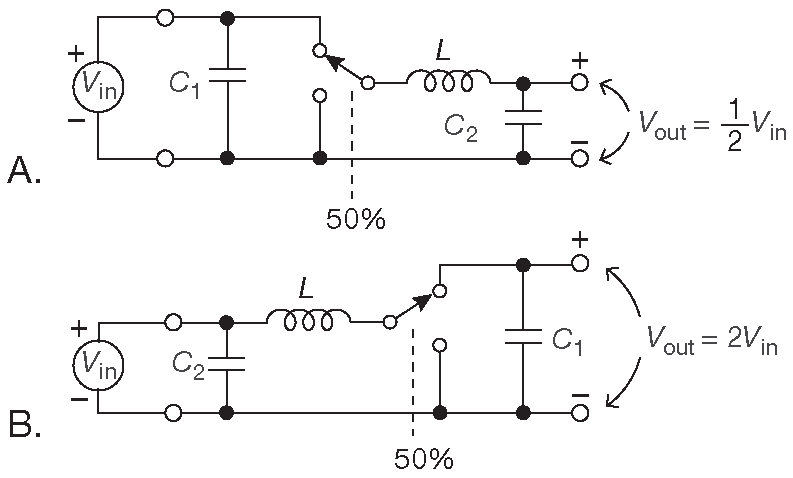
Рис. 1.52 Катушка индуктивности позволяет делать очень необычные вещи, например, увеличивать постоянное напряжение [* см. «Трансформатор постоянного тока» ( §X9.16 ) ]
Получение половины от входного напряжения не особо впечатляет. В конце концов, то же можно сделать с помощью делителя напряжения. Но, в отличие от делителя, эта схема не тратит энергию. Если отвлечься от неидеальности компонентов, все 100% энергии переходят со входа на выход. Схема активно используется в устройствах преобразования мощности и называется «синхронный понижающий преобразователь».
Переходим к схеме 1.52B , которая является вариантом схемы 1.52A [* развернули её, сердешную, задом наперёд] . Теперь баланс произведения вольт-секунда требует, чтобы выходное напряжение было в два раза выше входного. С помощью делителя такую схему уже не собрать. И опять выходной конденсатор ( теперь \( C_1 \) ) сохраняет заряд для усреднения выходного напряжения. Конфигурация называется «синхронный повышающий преобразователь».
Эти и другие ключевые преобразователи подробно разбираются в Части _9 [ §9.6 ] , а в табл. 9.5 собраны некоторые интегральные варианты, выполняющие такие задачи.
1.5.2 Трансформатор
Трансформатор - устройство, состоящее из двух тесно связанных катушек ( первичной и вторичной обмотки ). Переменное напряжение, поданное на первичную обмотку, появляется на вторичной с коэффициентом преобразования, равным отношению числа витков обмоток, а ток преобразуется в обратном отношении. Таким образом, мощность при прохождении через трансформатор не меняется. На рис. 1.53 показан схемный символ трансформатора с пластинчатым сердечником. Именно такие варианты используются в 60-герцовой сети.
Рис. 1.53 Схемный символ трансформатора
Трансформаторы имеют высокий КПД ( выходная мощность очень близка ко входной ), поэтому повышающий трансформатор даёт больше напряжения, но меньше тока. Заглядывая чуть вперёд, отношение витков трансформатора n изменяет импеданс с коэффициентом n2 . Если цепь вторичной обмотки разорвана, то в первичной течёт очень маленький ток.
Силовой трансформатор ( т.е. подключаемый к силовой питающей сети 120 или 240 V ) выполняет две важные функции. Он изменяет напряжение, обеспечивая нужный ( обычно меньший ) уровень для схемы, и «изолирует» электронное устройство от силовой сети, потому что обмотки трансформатора электрически изолированы друг от друга. Выпускаются трансформаторы с самыми разными напряжениями и токами вторичных обмоток - от одного до нескольких тысяч вольт и от миллиампер до сотен ампер. Типичный силовой трансформатор в современном приборе имеет вторичную обмотку на 10...50 V и на ток от 100 mA до 5A . В электронных преобразователях мощности используются сходные цифры, но мощность передаётся в импульсной форме и на гораздо большей частоте. Типичные цифры - от 50 kHz до 1 MHz .
Существуют трансформаторы для передачи сигналов из диапазона от десятков герц до десятков мегагерц и более. В радиодиапазоне, где работа обычно происходит в узком диапазоне частот, часто используют настроенные [* резонансные ] трансформаторы. Там же работают модели, построенные на линиях передачи. Трансформаторы, предназначенные для работы на высокой частоте, должны использовать сердечник из специального материала и конструкцию, снижающие потери, а низкочастотные модели, например, 60-герцовые отличаются гораздо более массивными сердечниками. Высоко- и низкочастотные трансформаторы не взаимозаменяемы.
1.5.2.A Особенности трансформаторов
==31
Краткий обзор выше обходил стороной возможные проблемы и особенности. Например, у трансформатора есть индуктивность, о чём говорит его схемный символ: действующая параллельная индуктивность ( индуктивность намагничивания ) и действующая последовательная индуктивность ( индуктивность рассеяния ). Индуктивность намагничивания вызывает появление тока первичной обмотки, даже если вторичная цепь разорвана, но, что важнее, она не позволяет сделать «трансформатор постоянного тока» [* на постоянном токе сопротивление идеальной индуктивности равно нулю, и параллельная индуктивность намагничивания будет закорачивать первичную цепь. Тем не менее, варианты есть, см. §X9.16 ] . А индуктивность рассеяния вызывает просадку напряжения, зависящую от тока нагрузки, и появление паразитных резонансных цепей с короткими импульсами и резкими фронтами [* см. §X9.6 ] . Кроме того, от идеала отдаляют: сопротивление обмоток, потери в сердечники, ёмкость между обмотками и магнитная связь с внешними цепями. В отличие от почти идеальных для большинства задач конденсаторов, недостатки индуктивных элементов существенно влияют на их работу. Тема развивается в Части X1 [* ##§X1.4 ] и Части _9 .
==31
28 На практике конденсаторы используются гораздо чаще. Происходит это, потому что реальные катушки индуктивности слишком сильно отличаются от идеала ( сопротивление обмотки, потери в сердечники и паразитная ёмкость ), а реальные конденсаторы гораздо ближе к идеальному воплощению ( см. Часть X1 [* ##§X1.4 ] ). Зато катушки незаменимы в ключевых источниках питания и резонансных контурах для радиочастотных схем. ) <-

