Приложение A. Математическая шпаргалка
==1097
Некоторое знание алгебры и тригонометрии абсолютно необходимо для понимания материала книги. Кроме того, полезен будет минимальный навык работы с комплЕксными числами и производными. Это приложение следует рассматривать в качестве краткой памятки по работе с комплЕксными числами, дифференцированию, некоторому набору полезных тригонометрических формул и действиям с экспонентами и логарифмами. Это не замена учебникам по указанным дисциплинам. Очень хорошо написанная, полезная и рекомендуемая книга по вычислениям разного рода D. Kleppner и N. Ramsey “Quick Calculus” [101] .
A.1 Тригонометрия, показательная функция и логарифм
Здесь простым списком приводятся некоторые полезные формулы. \[ x= \frac{-b±\sqrt{b^2-4ac}}{2a} \] является решением квадратного уравнения \(ax^2+bx+c=0\). \[ \begin{align*} \sin(x ± y) &= \sin(x) \cos(y) ± \cos(x) \sin(y), \\ \cos(x ± y) &= \cos(x) \cos(y) ∓ \sin(x) \sin(y), \\ \sin(2x) &= 2\sin(x) \cos(x), \\ \cos(x) \cos(y) &= (1/2) \Big[ \cos(x+y) + \cos(x-y) \Big], \\ \cos(x) \sin(y) &= (1/2) \Big[ \sin(x+y) — \sin(x-y) \Big], \\ \sin(x) \sin(y) &= (1/2) \Big[ \cos(x-y) — \cos(x+y) \Big],\\ e^{(x+y)} &= e^x e^y, \\ e^{(x-y)} &= e^x / e^y, \\ x^{(a/b)} &= \sqrt[b]{x^a}, \\ e^{[\ln x]} &= x, \\ \ln(x·y) &= \ln(x) + \ln(y), \\ \ln(x/ y) &= \ln(x) - \ln(y), \\ \ln(x^n) &= n·\ln(x), \\ \ln(e^x) &= x, \\ \ln(x) &= \ln(a)·\log_a(x) = \ln(10)·\lg(x) ≈ 2.3·\lg(x), \\ a^x &= e^{\big[x·\ln(a)\big]} \end{align*} \]
[* Два последних выражения относятся к преобразованию оснований логарифмов, т.е. показывают как перейти от одного основания логарифма к другому с примером для основания \(e\) ( натурального логарифма \(\ln\) ) и 10 ( десятичного логарифма \(\lg \) )].
A.2 Комплексные числа
КомплЕксным числом называется выражение вида \(\mathbf{N} = a + ib\) , где «\(a\)» и «\(b\)» - действительные числа, а «\(i\)» - квадратный корень из –1 . «\(a\)» называется действительной частью, а «\(b\)» - мнимой _1 [* «\(i\)» не входит в мнимую часть и является лишь её признаком ( множителем ) ] . Для указания на комплексное число используется жирное начертание или волнистое подчёркивание. Но, вообще-то, вы сами должны знать , о каком именно числе идёт речь!
Комплексные числа можно складывать, вычитать, умножать и т.д., как обычные действительные числа. \[ \begin{align*} (a + ib) + (c + id) &= (a + c) + i (b + d), \\ (a + ib) - (c + id) &= (a - c) + i (b - d), \\ (a + ib)·(c + id) &= (ac - bd) + i (bc + ad), \\ \frac{a + ib}{c+id} &= \frac{(a + ib)(c - id)}{(c + id)(c - id)} = \left(\frac{ac + bd}{c^2 + d^2}\right) + i\left(\frac{bc - ad}{c^2 + d^2}\right) \end{align*} \]
==1098
Все показанные действия выполняются привычным способом, как если бы «\(i\)» был обычным множителем в обычном арифметическом выражении. Отметим, что \(i^2=–1\) , и данное свойство используется при умножении. Деление упрощается умножением числителя и знаменателя на комплЕксное дополнение ( каковое дополнение получается изменением знака в мнимой части ). [* При такой операции мы не изменяем число, т.к. домножаем и числитель, и знаменатель на одно выражение, но избавляемся от мнимой части в знаменателе, что упрощает последующие манипуляции ] . Комплексное дополнение иногда обозначают звёздочкой, т.е., если \(\mathbf{N} = a + ib\) , то \(\mathbf{N^*} = a - ib\) . Величина ( модуль ) комплексного числа - действительное число, полученное умножением исходного комплексного числа на его дополнение и взятием квадратного корня из произведения \(|\mathbf{N}| = |a + ib|\) \(= \sqrt{(a + ib)(a — ib)}\) \(= \sqrt{a^2 + b^2} = \sqrt{\mathbf{NN^*}}\). Модуль произведения ( или частного ) комплексных чисел равен произведению ( или частному ) их модулей.
Действительная и мнимая часть комплексного числа \(\mathbf{N}\) иногда записываются как \(Re(\mathbf{N})\) , \(Im(\mathbf{N})\) . Получаются они из числа \(\mathbf{N}=a + ib\) тривиально: \(Re(\mathbf{N})=a\) , \(Im(\mathbf{N})=b\) . Данное действие может потребовать некоторого числа умножений, когда речь идёт о сложных выражениях, включающих члены с множителем «\(i\)».
Комплексному числу соответствует точка на комплексной плоскости, которая ничем не отличается от обычной двумерной плоскости с осями X и Y , при этом действительной части числа соответствует позиция по оси X , а мнимой - по оси Y ( см. рис. A.1 ). Соответственно, комплексное число можно записать как пару координат \[ a + ib ⇔ (a, b) \].
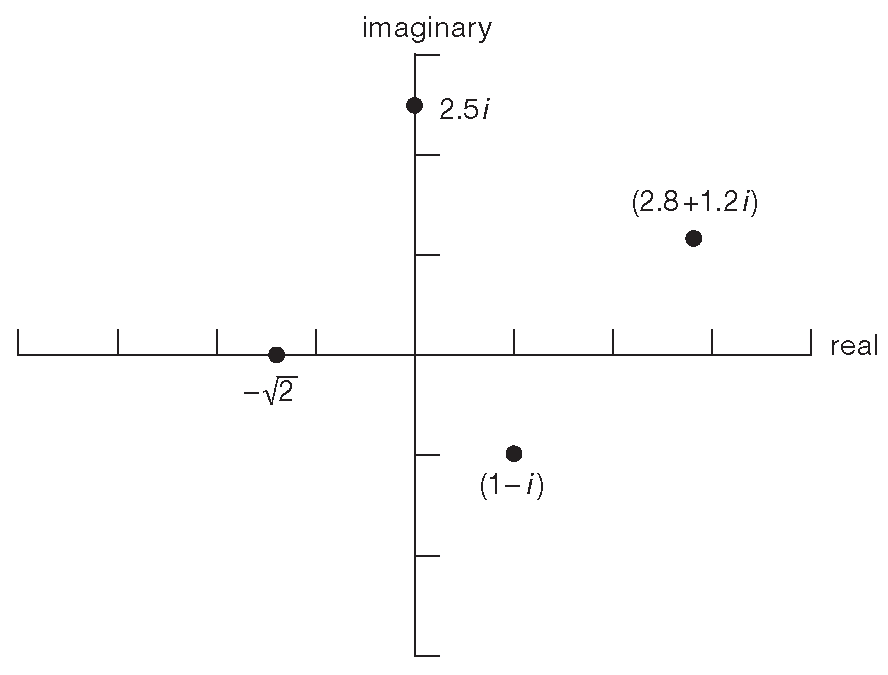
Рис. A.1 Комплексные числа на «комплексной плоскости»
Так же, как координаты на обычной плоскости, комплексные числа можно представлять в полярной форме «величина—угол». Например, число \(a + ib\) в соответствии с рис. A.2 можно записать как \[ a + ib = r∠Θ \] , где \(r=\sqrt{a^2+b^2}\) , а \(Θ=\arctan(b/a)\) _2 .
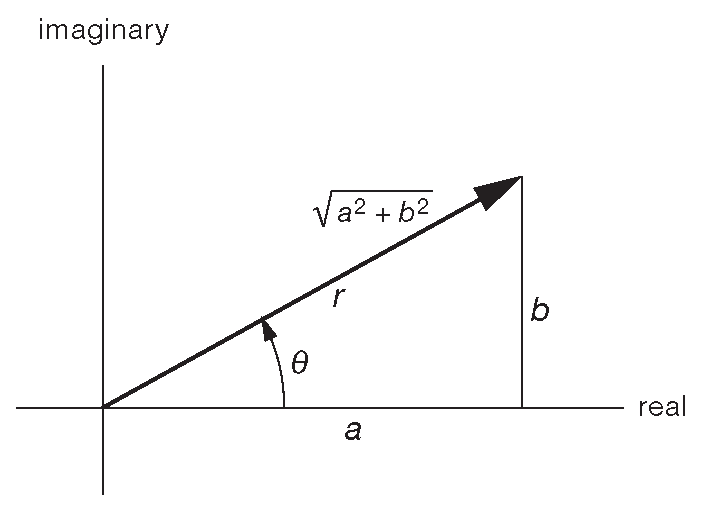
Рис. A.2 Комплексное число в полярной форме (величина и угол)
Есть ещё одна форма, которая использует примечательное соотношение \( e^{iΘ}=\cosΘ + i\sinΘ \) .
Рис. A.2a Связь между разными представлениями комплексного числа. [* Картинка ( 2 шт. ) честно скрадена с Википедии, поэтому на месте православной \(Θ\) ( см. рис. A.2A ) стоит еретическая \(ϕ\). Не научились они пока палочки на буквах правильно проводить. Но товарищи бдят, сигнализируют. Так разберёмся ! ]
Данное соотношение носит название «формула Эйлера» _3 и выводится разложением экспоненты \( e^{iΘ} \) в ряд Тейлора. В итоге получаются следующие соотношения [*] : \[ \begin{align*} \mathbf{N} &= a + ib = r(e^{iΘ}), \\ r &= |\mathbf{N}| = \sqrt{\mathbf{NN^*}} = \sqrt{a^2 + b^2}, \\ Θ &= \tan^{-1} (b/a), \quad \\ Θ &= \arctan (b/a), \end{align*} \] т.е. \(r\) и \(Θ\) - полярные координаты точки на комплексной плоскости. Полярная форма удобна для умножения комплексных чисел [* а также возведения их в степень и взятия корня ] . При умножении перемножаются модули и складываются углы, при делении - делятся модули и вычитаются углы. \[ (r_1·e^{[iΘ_1]} )(r_2·e^{[iΘ_2]}) = r_1·r_2·e^{[i(Θ_1+Θ_2)]} \]
[*] [* В иностранной литературе ( и на кнопках калькуляторов ! ) можно встретить запись вида \( \tan^{-1}() \). Она эквивалентна православной \( \arctan() \), т.е. обратна по результату функции \( \tan() \) и даёт на выходе величину угла в радианах. Используется для экономии письма ].
==1099
Наконец, для перевода из полярной в нормальную форму используется формула Эйлера: \[ re^{iΘ} = r\Big[\cos(Θ) + i\sin(Θ)\Big] . \] Иначе говоря, \[ Re(re^{iΘ}) = r\cos(Θ), \\ Im(re^{iΘ}) = r\sin(Θ) \]
Из этих соотношений легко вывести формулы суммы и разности тригонометрических функций. Можно не мучиться, заучивая эти заковыристые выражения. Просто считайте результат для \(e^{[i(x±y)]}\) .
Если требуется выполнить умножение комплексного числа на комплексную экспоненту, надо просто перемножить их. \[ \begin{align*} \mathbf{N} &= a + ib, \\ \mathbf{N}e^{iΘ} &= (a + ib)\Big[\cos(Θ) + i\sin(Θ)\Big], \\ &= \Big[a\cos(Θ) - b\sin(Θ)\Big] + i\Big[b\cos(Θ) + a\sin(Θ)\Big]. \end{align*} \]
При работе со схемами и сигналами аргумент \(Θ\) часто приходится выражать через угловую частоту \(Θ= ωt=2πft\). Таким образом \(V(t) = Re(\mathbf{V_0}·e^{iΘ}) = \mathbf{V_0}\cos(ωt)\).
A.3 Дифференцирование
Начнём с понятия функции \(f(x)\) , т.е. зависимости \(y\) для каждого \(x\) в виде \(y=f(x)\) . Функция \(f(x)\) должна быть однозначной , т.е. давать для любого \(x\) только одно значение \(y\) . Функцию \(y=f(x)\) можно рассматривать как график, см. рис. A.3 . Производная \(y\) по аргументу \(x\) ( обозначается \(dy/dx\) [* , а ещё \(y_x'\) или \(y|_x\) ] ) - это тангенс угла наклона графика \(y=f(x)\) . Если провести через некоторую точку графика \(y=f(x)\) касательную, тангенс её наклона будет равен производной \(dy/dx\) в этой точке . Т.к. производная имеет значение в каждой точке [* мы неявно предположили, что функция является дифференцируемой в каждой точке ] , она сама является функцией. На рис. A.3 наклон в точке \((1,1)\) равен \(2\) , а наклон в начале координат - нулю.
[* Обратите внимание на выражение \(dy/dx\). Оно однозначно определяет условие существования производной: угол наклона касательной к графику функции не должен равняться 90° или 180° ( вертикальная линия, параллельная оси Y ), при которых \(dx\)=0, а функция получает бесконечное число значений, т.е. входит в противоречие со своим определением ] .
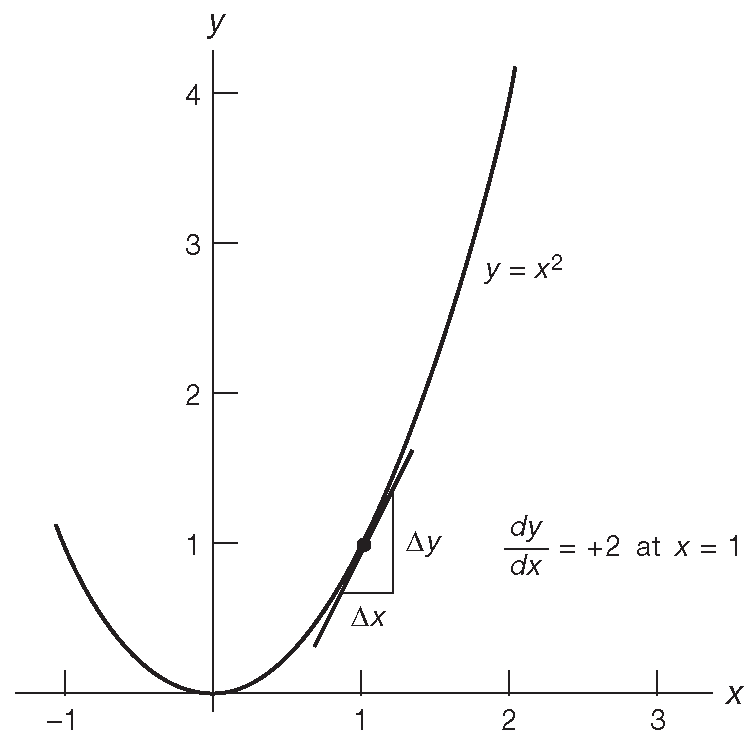
Рис. A.3 Однозначная функция \(f(x)=x^2\)
С математической точки зрения производная - предел отношения приращения функции ( \(Δy\) ) к приращению аргумента ( \(Δx\) ), когда приращение аргумента стремится к нулю.
Дифференцирование - тривиальная операция [* читай, однозначная, в отличие от интегрирования ] , выполняемая с помощью таблицы элементарных производных и правил вычисления производных сложных функций. Представлены функции аргумента «\(x\)», а «\(a\)» - некоторая константа.
A.3.1 Таблица элементарных производных
[* Таблица чуть расширена и слегка подправлена ] . \[ \begin{align*} &\frac{d}{dx}a &= &0 &\qquad &\frac{d}{dx}x &= &\quad1 \\ &\frac{d}{dx}ax &= &a &\qquad &\frac{d}{dx}x^n &= &\space nx^{n-1} \\ &\frac{d}{dx}e^x &= &e^x &\qquad &\frac{d}{dx}\ln(x) &= &\quad\frac{1}{x} \\ &\frac{d}{dx}a^x &= &a^x\ln(a) &\qquad &\frac{d}{dx}\log_a(x) &= &\quad\frac{1}{x\ln(a)} \\ &\frac{d}{dx}\sin(x) &= &cos(x) &\qquad &\frac{d}{dx}\cos(x) &= &-\sin(x) \\ &\frac{d}{dx}\tan(x) &= &\frac{1}{\cos^2(x)} &\qquad &\frac{d}{dx}\mathrm{ctg}(x) &= &-\frac{1}{\sin^2(x)} \\ &\frac{d}{dx}\mathrm{arcsin}(x) &= &\frac{1}{\sqrt{1-x^2}} &\qquad &\frac{d}{dx}\mathrm{acrcos}(x) &= &-\frac{1}{\sqrt{1-x^2}} \\ &\frac{d}{dx}\mathrm{arctg}(x) &= &\frac{1}{1+x^2} &\qquad &\frac{d}{dx}\mathrm{acrctg}(x) &= &-\frac{1}{1+x^2} \end{align*} \]
[* И на всякий случай, вдруг, кто не знает: \[ \frac{d}{dx}\Bigg(\int(x)dx\Bigg) = x \] т.е. производная интеграла функции \(x\) равна самой функции \(x\). Верно и обратное: \[ \int\Bigg(\frac{d}{dx}(x)\Bigg)dx = x + C \] интеграл производной функции \(x\) равен всё той же функции \(x\) ( с добавкой некоторой константы \(C\) - та самая неоднозначность операции интегрирования )].
[* В книге часто встречаются выражения вида \(i=C(dv/dt)=C\frac{d}{dt}v\) и т.п. Вот этих \(\frac{d}{dt}\) бояться не надо. В данном выражении просто сообщается, что ток заряда конденсатора пропорционален ( с коэффициентом «\(C\)» ) изменению напряжения на обкладках по времени. Если вспомнить, что \(I·t=Q=C·U\), флёр загадочности с выражения улетучивается окончательно. Скажем, скорость - это изменение пути по времени, или иначе: \(V=dS/dt\). Как видите, ничего страшного - просто форма записи. Физику, конечно, знать надо.
Отличие от школьной операции деления только в том, что форма \(\frac{dx}{dy}\) указывает на работу с малыми приращениями. Скажем, машина, движущаяся из точки A в точку B проходит расстояние S между ними за время T . Тогда можно сказать «школьным языком», что машина двигалась со скоростью \( V = S/T \). Можно сказать чуть математичнее \( V = ΔS/ΔT \), т.е. мы делим изменение расстояния на изменение времени ( запомнили показания одометра - счётчика километров - и часов в точке A и в точке B и провели расчёт ). Мы получили среднюю скорость. Дальше, если мы захотим узнать, была ли скорость машины постоянной или менялась на поворотах и перекрёстках, нам понадобятся промежуточные значения для пройденного пути для какого-то промежуточного времени. Спускаясь в эту кроличью нору с масштаба часов, через минуты, к секундам, мы обнаружим, что можем всё точнее указать среднюю скорость для промежутка времени, равного выбранному кванту отсчёта этого самого времени. И теперь мы уже имеем право использовать «математическую» запись \(dt\). Где проходит граница после которой «школьные» \(ΔT\) превращаются в «инженерные» \(dt\) указать затруднительно. Бескомпромиссные математики считают, что \(dt\) почти неотличима от нуля, но в обычной жизни всё зависит от масштаба наблюдателя. Для расстояния Москва-Воронеж десятиминутный промежуток времени вполне сойдёт за «мгновенное» значение.
Короче, «не бойтесь летать: ещё никто не остался в воздухе». Математика - вспомогательная гуманитарная дисциплина и, может быть, даже просто игра ума, которая удивительно хорошо подходит для описания явлений в точных ( естественных ) науках. Знать её столь же полезно, как знать «правильнописание» родного языка. Хотя, на мой старопердунский взгляд, современная молодёжь не обременяет себя ни тем, ни другим.
Дети, не будьте плохими! Будьте хорошими! Учите математику и родной язык, они укрепляют эрекцию организма! ]
Рис. A.4* Здесь расположена мотивирующая картинка. Её увидят только хорошие дети
==1100
A.3.2 Правила вычисления сложных функций
Пусть «\(u\)» и «\(v\)» - некоторые функции аргумента «\(x\)», а «\(a\)» - какая-то константа. Тогда верны следующие соотношения: \[ \begin{align*} &\frac{d}{dx}au(x) &= &a\frac{d}{dx}u(x)\\ &\frac{d}{dx}\Big(u(x)+v(x)\Big) &= &\frac{d}{dx}u(x) + \frac{d}{dx}v(x)\\ &\frac{d}{dx}\Big(u(x)·v(x)\Big) &= &v\frac{d}{dx}u(x) + u\frac{d}{dx}v(x)\\ &\frac{d}{dx}\Bigg(\frac{u(x)}{v(x)}\Bigg) &= &\frac{v\frac{d}{dx}u(x) - u\frac{d}{dx}v(x)}{v^2(x)}\\ &\frac{d}{dx}\Big(u\big[v(x)\big]\Big) &= &\frac{d}{dv}u · \frac{d}{dx}v(x) \end{align*} \]
A.3.3 Некоторые примеры дифференцирования
\[ \begin{align*} &\frac{d}{dx}\big(x^2\big) &= &2x \\ &\frac{d}{dx}\Big(x^{-(1/2)}\Big) &= &-\frac{1}{2}x^{-(2/3)}\\ &\frac{d}{dx}(x·e^x) &= &e^x+xe^x\\ &\frac{d}{dx}\Big(e^{[-x^2]}\Big) &= &-2x·\big(e^{-x^2}\big) \\ &\frac{d}{dx}\big(a^x\big) &= &\frac{d}{dx}\big(e^{x\ln(a)}\space\big) &= &a^x\ln(a) \end{align*} \]
После того, как функция продифференцирована, часто возникает необходимость узнать значение производной в некоторой точке и найти точки минимального или максимального значения функции ( экстремумы ). Для нахождения значения производной в точке надо просто подставить в формулу производной нужный аргумент [* т.е., если дифференцировали по «\(x\)», то значение «\(x\)» в нужной точке и подставляем ] , а для поиска экстремума надо приравнять производную нулю и решить получившееся уравнение относительно аргумента. Например, для функции \(y=x^2\) производная [* по «\(x\)», потому что других переменных нет ] равна \(y'=2x\) . В точке \(x=0\) производная \(y'=2×0 = 0\), в точке \(x=1\) производная \(y'=2×1 = 2\) [* а значение функции \(y=1^2 =1\). В курсе математики такие задачи объясняются в разделе анализа графиков ] .
==1100
[ A.4* Ряды ]
[*
Ниже приводится очень наглядная картинка разложения в ряд того самого Фурье, обнаруженная в документе scda017 фирмы Texas Instruments. Здесь показан спектр прямоугольного сигнала, т.е. набор составляющих его гармоник. Обратите внимание как влияет число членов ряда, участвующих в формировании результата, на форму восстановленного сигнала. Именно такую картину можно получить, если пропустить сигнал с частотой \(Freq\) через ФНЧ с полосой \(BW\), который будет давить высокочастотные составляющие исходного спектра, «заваливая» фронты. Причём, возможно, пропускать сигнал через фильтр низких частот вы и не предполагали, «само так получилось» ( см. рис. 12.31 ).
Можно также прикинуть какую полосу должен иметь цифровой осциллограф, чтобы считаться «измерительным прибором» на частоте вашего сигнала.
В §7.1.5.A , а также на рис. 6.6 и X9.61 можно посмотреть, как получают первую гармонику из прямоугольного сигнала, которая, кстати, больше по амплитуде этого самого сигнала ].
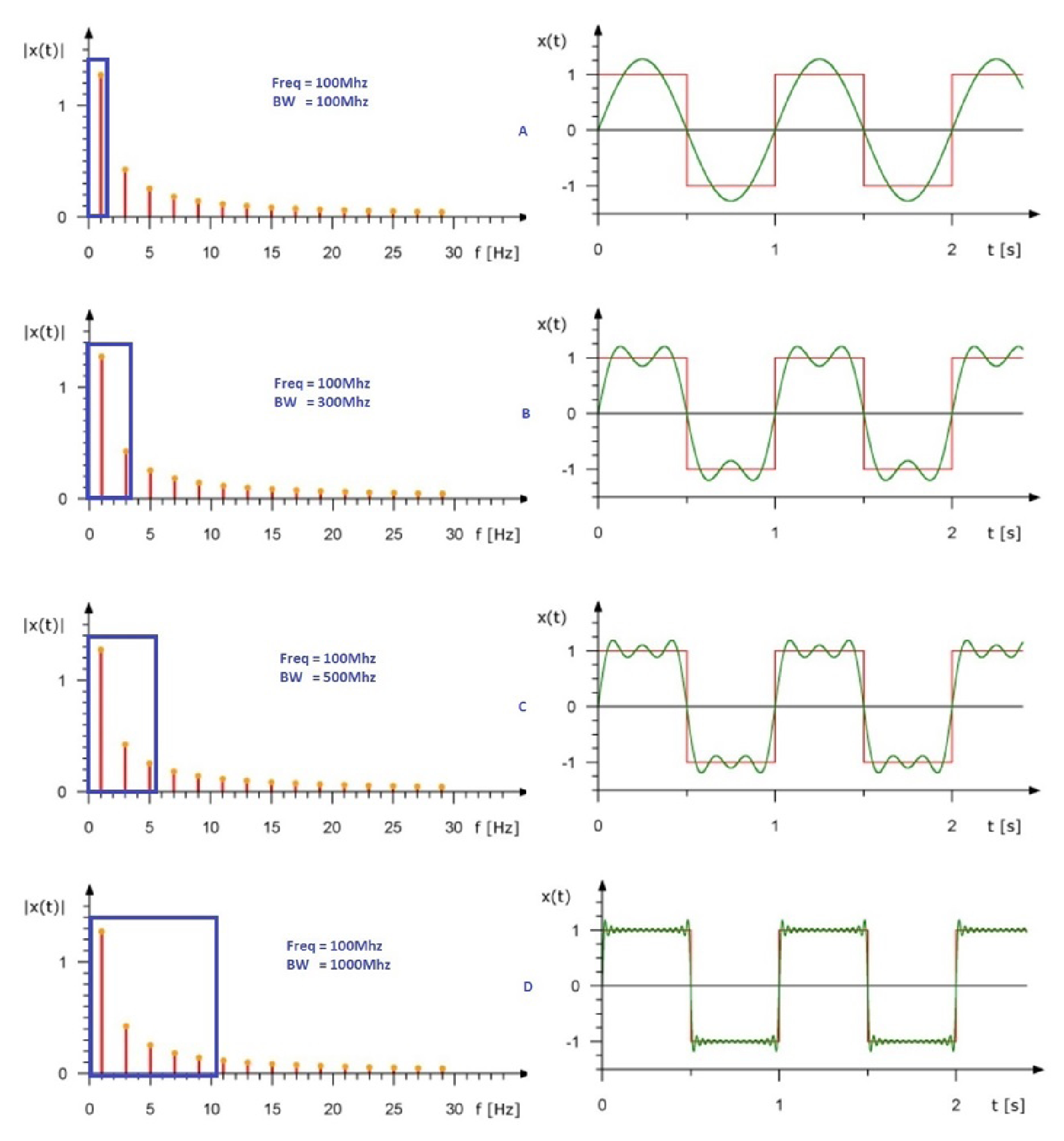
Рис. A.5* «Рис.2 Прямоугольный сигнал с разным числом гармоник»
==1100
1 Инженеры-электротехники избегают математического обозначения \(i≡\sqrt{-1}\) и используют для этих целей «\(j\)» , чтобы не допустить неоднозначности, т.к. «\(i\)» используется для малых изменений тока. Инженерная нотация используется в книге везде, кроме этого приложения, потому что иначе авторов заклевали бы коллеги-математики. <-
2 Предупреждение: формула возвращает \(Θ\) только в диапазоне от \(–π/2\) до \(+π/2\). Чтобы получить корректное значение во всех квадрантах, требуются знаки при «\(a\)» и при «\(b\)» [ см. рис. A.1 ] . Одного лишь знака произведения недостаточно. <-
3 Леонард Эйлер (Leonhard Euler), произносится “oiler”. <-

