1.7 (I) Импеданс и реактивность
==40
Предупреждение . В этой главе много математики, которую можно пропустить, если совсем не идёт, но необходимо в обязательном порядке посмотреть выводы и графики.
[* Полагаю, данная фраза без изменения взята из первого издания, к которому она подходила целиком и полностью. К сожалению, сейчас она явно вводит читателя в заблуждение, и предложенный способ, скорее всего, не сработает. Эта редакция книги набита формулами под завязку. Их стало очень много по сравнению с первым изданием ( и, к сожалению, в них очень много ошибок ). Обойтись в современной электронике без математики невозможно и этот скилл таки придётся прокачивать. Поверьте моему скромному опыту: отсутствие математической подготовки ВСЕГДА будет «жать в плечах». И, да, сейчас ещё можно найти в электронике нишу, где математика нужна не сильно или имеет узко очерченные рамки, но число и объём таких областей постоянно и неуклонно сокращается ].
Схемы с конденсаторами и индуктивностями сложнее, чем обсуждавшиеся ранее схемы из резисторов, потому что поведение конденсаторов и катушек индуктивности зависит от частоты. Коэффициент деления «делителя напряжения», включающий конденсатор или катушку, будет зависеть от частоты. Кроме того, схемы, содержащие конденсаторы и индуктивности ( их называют реактивными компонентами ) «портят» входной сигнал прямоугольной формы.
Тем не менее, конденсаторы и катушки - линейные элементы в том смысле, что амплитуда выходного сигнала, независимо от формы, увеличивается в точной пропорции ко входной амплитуде. Данный факт имеет много следствий, наиболее важное из которых следующее. Выход линейной схемы, на которую подаётся синусоидальный сигнал некоторой частоты f , является синусоидальным сигналом той же частоты, возможно, с иной амплитудой и фазой .
==41
Это примечательное свойство схем, построенных из резисторов, конденсаторов и катушек ( и ещё линейных усилителей ), позволяет изучать такие схемы, выясняя, как выходное напряжение, амплитуда и фаза зависят от напряжения входного синусоидального сигнала одной частоты , даже если работать придётся с другими сигналами. График итогового частотного отклика [* АЧХ ] , на котором отношение входа к выходу нарисованы для каждой частоты синусоидального сигнала, позволяет получить представление о том, что произойдёт с сигналом любой формы. Например, динамик некоего «бумбокса» может иметь частотную характеристику, показанную на рис. 1.87 . В данном случае «выход» - не напряжение, а звуковое давление. От динамика обычно хотят «плоской» частотной характеристики. Т.е. график звукового давления по частоте должен быть плоским в слышимом диапазоне частот. В примере недостатки излучателя можно исправить пассивным фильтром с обратной частотной характеристикой в канале усиления.
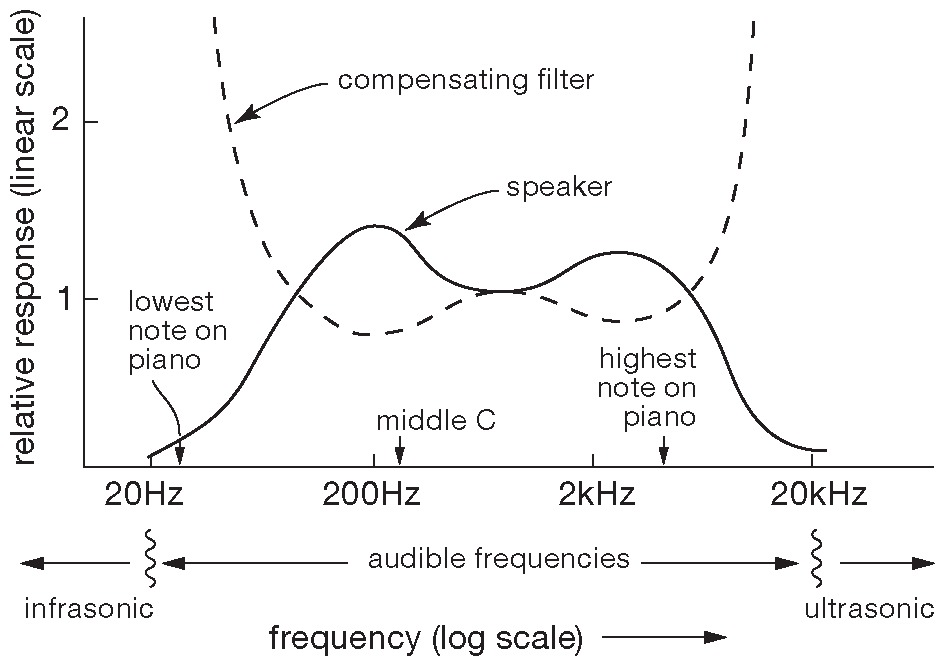
Рис. 1.87 Пример анализа в частотной области: нормализация частотной характеристики динамика в «бумбоксе». Самая низкая ( «A0» ) и самая высокая ( «C8» ) ноты фортепиано имеют частоты 27.5 Hz и 4.2 kHz соответственно. Первая на четыре октавы ниже «A440», вторая на четыре октавы выше «middle C». [* Только не спрашивайте, зачем нам эти сведения]
Вскоре будет показано, что, если заменить термин «сопротивление» на «импеданс», станет возможно обобщить закон Ома, распространив его действие на любую схему, собранную из линейных компонентов ( резисторов, конденсаторов и катушек ). Импеданс ( обобщённое или полное сопротивление ) можно рассматривать как составную часть закона Ома для схем с конденсаторами и катушками.
Несколько определений. Импеданс ( \(\mathbf{Z}\) ) – «обобщённое сопротивление». Конденсаторы и катушки, в которых угол между током и напряжением всегда равен 90° , - реактивные элементы, т.е. имеют реактивное сопротивление ( \(X\) ). Резисторы, у которых ток и напряжение всегда в фазе, «резистивны», т.е. имеют активное сопротивление ( \(R\) ). В общем случае в схемах, содержащих резистивные и реактивные компоненты, напряжение и ток в некоторой точки будет иметь какое-то промежуточное состояние фазы, описываемое уравнением для комплексного импеданса: импеданс = активное_сопротивление + реактивное_сопротивление или \( \mathbf{Z}=R+jX \) ( подробнее об этом позже ) 36 . Дальше будут часто встречаться выражения вида: «импеданс конденсатора на этой частоте...». Термин «реактивное сопротивление» здесь не используется, потому что импеданс закрывает обе составляющие. Термин «импеданс» будет встречаться, даже если известно, что речь идёт об активном сопротивлении. «Импеданс источника» или «выходной импеданс» обозначают эквивалентное сопротивление Тевенина для некоторого источника сигнала. То же относится и ко «входному импедансу».
Дальше пойдёт разговор о синусоидальных сигналах в схемах. Анализ устройства более сложным сигналом труднее, предполагает использование дифференциального счисления или разложения сложного сигнала в ряд Фурье ( т.е. в набор синусоид ). К счастью данные методы требуются нечасто.
1.7.1 Частотный анализ реактивных схем
Начнём с рассмотрения синусоидального напряжения \( V( t )=V_0\sin(ωt ) \) на конденсаторе ( рис. 1.88 ). Ток равен
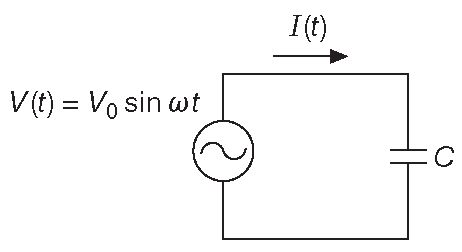
Рис. 1.88 Конденсатор под воздействием синусоидального напряжения
\[ I( t )=C\frac{dV}{dt} = I( t )=C\frac{d}{dt}( V_0\sin(ωt )) =C ω V_0\cos( ω t ), \] т.е. ток имеет амплитуду \( CωV_0\) , а его фаза опережает напряжение на 90° . Если забыть о фазах и учитывать амплитуды, ток будет \[ I = \frac{V}{^{1}/_{( ω C)}}. \]
Здесь полезно будет напомнить, что \(ω=2πf\) . Конденсатор ведёт себя как частотно зависимый резистор \(R=\frac{1}{ωC}\) , но, кроме того, ток в нём опережает напряжение на 90° ( рис. 1.89 ).
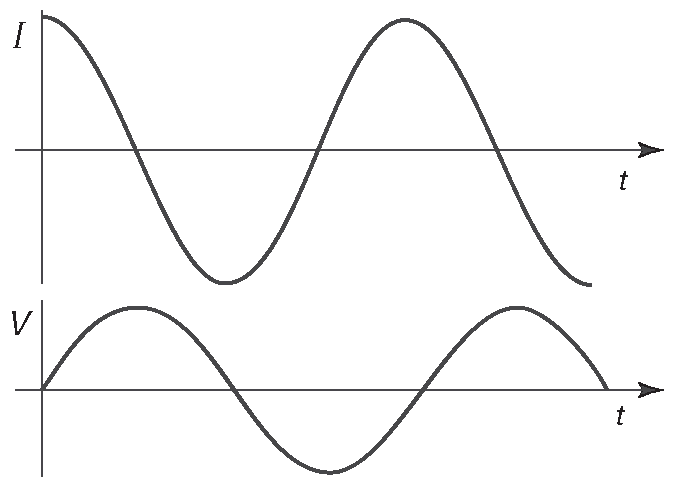
Рис. 1.89 Ток в конденсаторе обгоняет синусоидальное напряжение на 90°
Например, через конденсатор 1 μF , подключённый к сети 115 Vrms@60 Hz потечёт ток \[ I = \frac{115}{^{1}/_{( 2 π ×60 ×10^{-6})}} = 43.4\space mA(rms). \]
Достаточно скоро в рассмотрение будет включён сдвиг фаз и смежные понятия, и потребуется комплексная алгебра, которая приводит в ужас новичков. А сейчас удобный момент для развития понимания поведения в частотной области базовых схем, включающих конденсаторы. До поры различие фаз тока и напряжения синусоидального сигнала на конденсаторе учитываться не будет.
==42
Выше показано, что отношение модулей напряжения и тока частотой \( ω \) в конденсаторе равно \[ \frac{|V|}{|I|}=\frac{1}{ ω C}. \]
Его можно рассматривать в качестве некоторого «сопротивления» - пропорции, в которой приложенное напряжение соотносится с протекающим током. Официальное название величины реактивное сопротивление , а обозначение \( X \) , т.е. \( X_C \) - реактивное сопротивление конденсатора 37 . \[ X_C=\frac{1}{ ω C} \qquad [1.26] \]
Это означает, что чем больше ёмкость, тем меньше реактивное сопротивление. Двухкратное увеличение ёмкости потребует удвоенного тока заряда-разряда при том же напряжении за то же время ( \(I=C( dV/dt )\) ). По тем же причинам реактивное сопротивление снижается с увеличением частоты. Увеличение частоты в два раза ( при постоянном \( V \) ) удваивает частоту перезарядки, т.е. требует удвоенного тока, иначе говоря, уменьшает в два раза реактивное сопротивление.
Из изложенного ясно, что конденсатор можно назвать «частотно-зависимым резистором». Иногда это полезно, иногда наоборот. Ниже рассматриваются несколько схем, для которых упрощённое рассмотрение даёт хороший результат. Позднее общее представление будет дополнено комплексной алгеброй, позволяющей получить точные результаты. Не забывайте, что упрощённое рассмотрение даёт только приблизительный ответ. Чтобы подчеркнуть данный факт, будет использоваться символ «\(≍\)» в значении «приближённое равенство», а само выражение будет снабжаться предупреждением «approx!» - «примерно».
1.7.1.A Примерные соотношения для RC фильтра низких частот
Схема на рис. 1.90 называется фильтром низких частот , потому что она пропускает на выход сигналы низкой частоты и блокирует сигналы высокой. Здесь имеет смысл рассматривать цепь как частотно-зависимый делитель. Нижняя половина делителя ( конденсатор ) уменьшает реактивное сопротивление с увеличением частоты, поэтому отношение \( V_{out}/V_{in} \) уменьшается в той же степени.
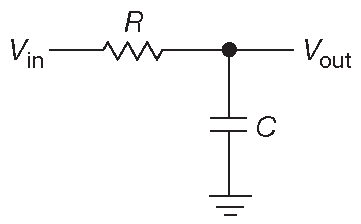
Рис. 1.90 Фильтр нижних частот
\[ \frac{V_{out}}{V_{in}} ≍ \cfrac{X_C}{R+X_C}=\cfrac{\cfrac{1}{ ω C }}{R+\cfrac{1}{ ω C}}= \cfrac{1}{1+R ω C} \quad . \text{(approx!)} \quad [1.27] \]
График данного отношения приведён на рис. 1.91 ( и заодно график для фильтра высоких частот ) вместе с точными данными, которые будут посчитаны в §1.7.8 .
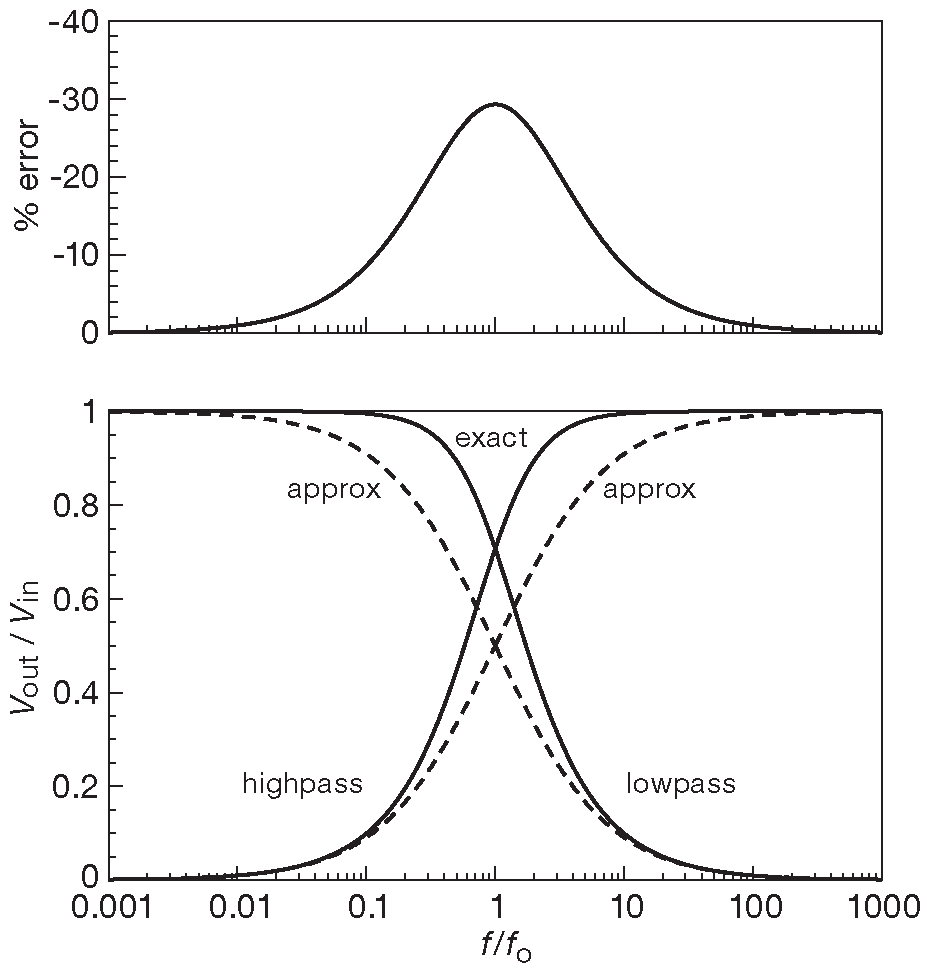
Рис. 1.91 Частотный отклик одной секции RC фильтра. Показаны два результата: пунктиром - приблизительный ( без учёта фазы ) и сплошной линией - точный. Сверху показана величина ошибки - разница «примерно-точно»
Можно заметить, что схема полностью пропускает низкие частоты и блокирует высокие. На низкой частоте реактивное сопротивление конденсатора очень велико, поэтому фильтр выглядит как маленький резистор поверх большого. На высокой всё наоборот. Переход от «пропускания» к «задержанию» ( часто называемый срезом ) происходит на частоте \( ω_0 \) , где реактивное сопротивление конденсатора 1/( \(ω_0 C\) ) равно сопротивлению \(R\) , т.е. \( ω_0\)=1/(\(RC\)). На частотах, далеко отстоящих от \( ω _0 \) ( где произведение \( ω RC\)≫1 ) выходной сигнал уменьшается с ростом частоты, т.к. реактивное сопротивление конденсатора уменьшается по закону 1/\(ω\) . По графику видно, что хотя в упрощённом расчёте фаза не учитывается, уравнение и график достаточно точны для низких и высоких частот. Ошибка заметна только в зоне перехода, где корректный коэффициент деления \[ \frac{V_{out}}{V_{in}}=\frac{1}{\sqrt2} ≈ 0.7, \] а не 0.5 , как получается по уравнению [1.27] 38 .
==43
1.7.1.B Примерные соотношения для RC фильтра верхних частот
Здесь R и C поменяны местами ( рис. 1.92 ), и поведение схемы противоположно: высокие частоты пропускаются, низкие - задерживаются. Рассматривая цепь как частотно-зависимый делитель и игнорируя сдвиг фаз, получаем ( рис. 1.91 ):
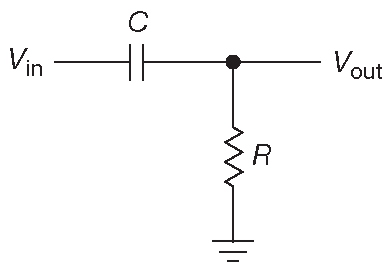
Рис. 1.92 Фильтр верхних частот
\[ \frac{V_{out}}{V_{in}} ≍ \frac{R}{R+X_C}=\frac{R}{R+\cfrac{1}{ω C}}=\frac{R ω C}{1+R ω C} \quad \text{(approx!)} \quad [1.28] \]
Высокие частоты ( выше точки \(ω_0\)=1/( \(RC\) ) ) проходят насквозь, потому что реактивное сопротивление конденсатора гораздо меньше \(R\) , а частоты ниже \(ω_0\) блокируются ( реактивное сопротивление гораздо выше \(R\) ). Как и в случае ФНЧ график и формула дают хорошую точность вдали от \(ω_0\) и только на ней отношений \[ \frac{V_{out}}{V_{in}}=\frac{1}{\sqrt2}. \]
1.7.1.C Разделительный конденсатор
Иногда требуется пропускать через схему какие-то частоты, но блокировать постоянный уровень, который может присутствовать в сигнале ( откуда он может взяться будет ясно из разговора об усилителях в Части _2 ). Задачу можно решить с помощью RC фильтра верхних частот, но требуется правильно выбрать частоту среза. ФВЧ всегда блокирует постоянное напряжение, поэтому требуется подобрать номиналы так, чтобы \(ω_0\) располагалась ниже всех представляющих интерес частот. Это один из самых частых вариантов использования конденсаторов, которые зовутся в этом случае разделительными .
Например, любой звуковой усилитель имеет на входе емкостную развязку, потому что заранее неизвестно, какой постоянный уровень будет у входного сигнала. Здесь требуется, чтобы выбранные R и C пропускали нужные частоты ( от 20 Hz до 20 kHz ) без ослабления ( аттенюации ), т.е. условие для произведения \(RC\)>1/\(ω_{min}\) . В этом случае можно выбрать \( f_{min} \)≈5 Hz , тогда \(RC\)=1/\(ω_{min}=1/( 2 π f) \) или \(RC\)≈30 ms .
Получили произведение, а требуются конкретные номиналы \(R\) и \( C \) . Выбор надо делать, учитывая, что входной сигнал видит нагрузку в виде \(R\) на рабочих частотах ( где реактивное сопротивление конденсатора мало, и сам он больше похож на кусок провода ). Поэтому номинал \(R\) должен быть разумной нагрузкой для источника: не слишком низкоомным, чтобы не перегружать его, и не слишком высокоомным, чтобы не ловить наводки от соседнего оборудования. В коммерческих схемах часто можно видеть 10 kΩ . Можно на нём и остановиться. Соответствующая ёмкость составит 3.3 μF ( рис. 1.93 ). Схема, стоящая после фильтра, должна иметь входное сопротивление много большее, чем 10 kΩ , чтобы не нагружать фильтр [* сдвигаяя его частоту среза вверх] . А источник сигнала должен быть способен работать на нагрузку 10 kΩ без потери амплитуды ( аттенюации ) и выдерживать эффекты от воздействия фильтра [* изменение импеданса и фазы по частоте ] . Следует отметить, что приближённая оценка, не учитывающая сдвиг фаз достаточно точна для этой схемы, потому что рабочая полоса полностью укладывается в полосу пропускания, где фаза меняется незначительно.
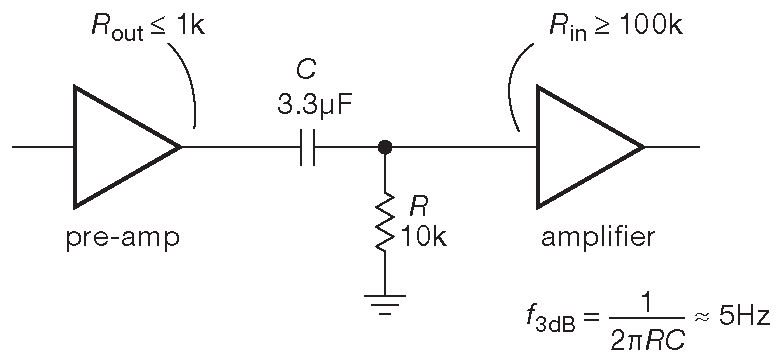
Рис. 1.93 «Разделительный конденсатор» . Фильтр высоких частот, для которого все интересующих частоты сигнала попадают в полосу пропускания
В этой главе схемы рассматриваются в частотной области по реакции на синусоидальный сигнал частотой \( f \) . Но бывает полезен и анализ во временнОй области, где разделительный конденсатор влияет на фронты импульсов и прямоугольных сигналов. В этой ситуации приходится разбираться с искажениями в виде просадки вершины импульса и выброса на переходах ( вместо изменения амплитуды и сдвига фазы [* одночастотного] синусоидального сигнала ). Во временной области речь идёт о противодействии искажению импульса длительности T за счёт увеличения постоянной времени так, чтобы \(τ=RC\)≫T . Тогда просадка вершины импульса близка к T/τ ( каковая просадка идёт в комплекте со сравнимым по амплитуде выбросом на следующем переходе ).
Часто требуется знать реактивное сопротивление конденсатора на некоторой частоте, например, при расчёте фильтра. На рис. 1.100 в §1.7.8 приводится очень удобный график, закрывающий большой диапазон емкостей и частот и дающий величину \[ X_C=\frac{1}{2 π fC}. \]
==44
1.7.1.D RC фильтры в качестве источника и нагрузки
Пример с разделительным конденсатором в аудио-тракте поднимает тему воздействия RC цепочек на схему. В §1.2.5.A в контексте делителей напряжения обсуждалась необходимость перекомпоновки схемы таким образом, чтобы сопротивление нагрузки не образовывало бы с эквивалентным сопротивлением источника заметного делителя.
Те же соображения можно применить и здесь, но с обобщением сопротивления до импеданса , включающего реактивную составляющую для конденсаторов и катушек. Таким образом, импеданс источника в общем случае должен быть мал по сравнению с импедансом нагрузки 39 . Будет корректно отметить, что без учёта сдвига фаз импеданс конденсатора равен его реактивному сопротивлению, что будет подтверждено расчётами чуть позднее.
Но в данном случае интересен входной и выходной импеданс RC цепочки ( фильтров низких и высоких частот ). Вопрос кажется достаточно сложным, ведь речь идёт о четырёх импедансах, меняющихся с частотой. Но если задать его правильно, то ответ будет простой и одинаковый для всех случаев.
Во-первых, условимся, что в каждом случае на другом конце фильтра всё хорошо. Иначе говоря, когда нужен входной импеданс RC цепи, то на другом конце высокоомный вход, а когда выходной, на другом конце источник сигнала с низким внутренним сопротивлением ( Тевенина ). Во-вторых, мы исключаем колебания импеданса от частоты и выясняем только значение для наихудшего случая . Другими словами, нас интересует максимальный выходной ( такой выход чувствительней к нагрузке ) и минимальный входной ( такой вход труднее раскачать ) импедансы фильтра.
В такой постановке ответ на редкость прост. В обоих случаях наихудшее значение импеданса равно \(R\) .
Упражнение 1.23
Покажите, что это утверждение корректно.
Поэтому, если требуется повесить RC фильтр низких частот на выход усилителя с выходным сопротивлением 100 Ω , начинать надо с \(R\)=1 kΩ и подбирать ёмкость под нужную частоту среза. При этом надо смотреть, чтобы после фильтра был вход с импедансом не ниже 10 kΩ . Ошибиться тут сложно.
Упражнение 1.24
Разработайте «двухступенчатый» полосовой RC фильтр, в котором ФВЧ на входе имеет срез на 100 Hz , а ФНЧ на выходе - 10 kHz . Предполагается, что импеданс источника 100 Ω . Какой минимальный выходной импеданс будет иметь такой фильтр, и каков минимальный рекомендованный импеданс нагрузки?
1.7.2 Реактивное сопротивление катушек индуктивности
Прежде чем браться за полностью корректный разбор импеданса, набитый комплЕксными экспонентами и тому подобными вещами, подсчитаем по упрощённой формуле реактивное сопротивление катушки индуктивности.
Расчёт идёт по прежней схеме. Мысленно подадим синусоидальное напряжение с круговой частотой \(ω\) на катушку индуктивности \(L\) так, чтобы через неё тёк ток \(I( t )=I_0\sin( ω t )\) 40 . Тогда напряжение на концах обмотки будет \[ V( t )= L\frac{dI}{dt}=L\frac{d}{dt}(I_0\sin( ω t ))=L ω I_0\cos( ω t ). \]
Отношение модулей напряжения и тока даст выражение в единицах сопротивления, которое зовут реактивным сопротивлением \[ \frac{|V|}{|I|}=\frac{L ω I_0}{I_0}= ω L. \]
Таким образом, для индуктивности имеем \[ X_L = ω L. \qquad [1.29] \]
Катушки индуктивности, подобно конденсаторам, имеют частотно-зависимое реактивное сопротивление, но теперь оно растёт с ростом частоты ( а у конденсатора снижается ). В самом первом приближении катушку индуктивности в последовательном включении можно использовать для передачи постоянного тока и низких частот ( где реактивное сопротивление мало ) и задержания высоких частот ( где реактивное сопротивление велико ). Катушки часто именно так и используют, особенно в устройствах радиочастотного диапазона. В этой области их часто называют дросселями .
1.7.3 Напряжения и токи как комплексные величины
Дальнейшие объяснения требуют использования теории комплексных чисел. Математику можно пропустить, но итоговые результаты потребуются для дальнейшего материала. Глубокие знания математики для понимания остального материала книги не требуются. В остальных частях она почти не используется. [* Похоже, этот абзац остался от первого издания. Именно он вдохновил меня на подвиги в электронике. Но для третьей редакции данный посыл, к сожалению, не верен] . Следующий параграф будет самым трудным для неподготовленного читателя, но дело того стОит .
==45
Ранее утверждалось, что в синусоидальном сигнале некоторой частоты, проходящем через схему, может возникать сдвиг фаз между напряжением и током. Но в схеме, состоящей только из линейных компонентов ( резисторов, конденсаторов, катушек ) величины токов в любой точке пропорциональны входному напряжению. Поэтому должен существовать способ обобщить все напряжения, токи и импедансы через некоторый универсальный закон Ома. Очевидно, что для полной спецификации, скажем, тока в некотором узле одного числа недостаточно, т.к. нужно передать информацию как о величине, так и о фазе.
Можно, конечно, записывать токи и напряжения в непосредственной форме, например \( V( t )=23.7\sin( 377t+0.38) \), но, очевидно, что ту же информацию можно передать, используя комплЕксные числа для представления напряжений и токов. После этого мы можем использовать возможности алгебры комплексных чисел для действий над комплексными представлениями, вместо утомительных вычислений с участием непосредственных синусоидальных функций. Токи и напряжения - физические параметры, меняющиеся во времени, и требуются правила преобразования такого параметра в комплЕксное представление и обратно. Напомним ещё раз, что речь идёт об одной синусоидальной частоте \(ω\) , и будем следовать следующим правилам.
- Напряжения и токи представляются комплЕксными числами \(\mathbf{V}\) и \(\mathbf{I}\) . Напряжение \( V_0[\cos( ω t+ φ )]\) представляется комплексным числом \(\mathbf{V}=V_0[e^{j φ }]\) [* обратите внимание, используется начальная фаза φ , круговая частота ω не участвует] .
- Мы получаем актуальное значение напряжения и тока, умножив их комплексное представление \(\mathbf{V}\) на \( (e^{j ω t}) \) и взяв действительную часть результата [* выкинув слагаемое, содержащее «\(j\)» ] : \( V( t ) = \mathscr{Re}(\mathbf{V}e^{j ω t}) \) , \(I( t ) = \mathscr{Re}(\mathbf{I}e^{j ω t}) \) .
Комплексная экспонента \([e^{j ωt }]\) в соответствии с уравнением [* Эйлера ] раскладывается \[ \mathbf{V}[e^{j ωt }]=\mathbf{V}[\cos ωt +j\sin ωt] , \] где \(j=\sqrt{-1}\) . ( В электротехнике комплексные числа записываются с использованием буквы «j» , вместо «i» , чтобы не путать последнюю с обозначением малого изменения тока ).
Позволил себе полностью переписать этот абзац, потому что в оригинале понять ничего нельзя. Подробности с картинками в Приложении _A ( §A.2 ).
Начало переписанного абзаца.
- Напряжение ( мы говорим о синусоидальном сигнале ) \( V( t )=23.7\sin( 377t+0.38) \) выражено в исходной «аналитической» форме ( амплитуда 23.7 единиц, круговая частота 377 радиан в секунду, начальная фаза 0.38 радиан ), т.е. \( V_0\cos( ω t+ φ) \) , которая содержит все данные о сигнале, но неудобна для работы.
-
Это же напряжение представляется комплЕксным числом \(\mathbf{V}\) , которое может быть выражено в четырёх формах:
- «полярной» ( амплитуда—угол ) \( 23.7∠0.38\); удобна для записи и только;
- «тригонометрической» ( проекция на ось «X» ( теперь её зовут «Re» ) + проекция на ось «Y» ( теперь «Im» ) ) \( 23.7\cos0.38+j23.7\sin0.38\) в непосредственном виде используется редко, но служит переходом к
- «алгебраической» ( \(a+jb\) или «координата по оси Re» + j«координата по оси Im» ) \( 23.7\cos0.38+j23.7sin0.38\) = \( 22.00+j8.79\) удобна для расчётов и активно используется именно для этого;
- и, наконец, в «показательной форме» ( \( V_0e^{j(ωt + φ)}\) ) - в виде комплЕксной экспоненты \( 23.7e^{j( 377t+0.38)}\) активно используется для расчётов.
-
Дальше показательная форма претерпевает следующие изменения \[ \begin{align} &V_0e^{j(ωt + φ)}\space = \\ &V_0e^{jωt}·e^{jφ} = \\ (&V_0e^{jφ})·e^{jωt} \quad . \end{align} \] Мы получили постоянный коэффициент - комплЕксную амплитуду \( \mathbf{V}=V_0e^{jφ} \) ( т.е. вектор длиной \(V_0\), выходящий из начала координат под углом \(φ\) ) и экспоненциальную часть \( e^{jωt} \) , которая зависит от времени ( та самая частота сигнала: именно с этой частотой вектор вращается вокруг начала координат ). Иначе говоря, комплЕксная амплитуда ( собственно «комплЕксное представление» ) отличается от обычной амплитуды тем, что содержит в себе пару «величина-угол» ( амплитуда \( V_0\) - начальная фаза \(φ\) ) и представляется на комплЕксной плоскости вектором ( те самые «длина и угол от исходной точки в начале координат» ). Она используется при вычислении комплЕксных импедансов и прочих расчётов с участием гармонических сигналов. Экспоненты в обеих частях в соответствии с уравнением Эйлера раскладывается в тригонометрическую форму \( e^{j α }=\cos α +j\sin α = Re(α) + jIm(α) = a + jb \) ( почему, собственно, и используется ).
Актуальное значение напряжения в конкретный момент времени t получаем, умножив комплексную амплитуду \( \mathbf{V} \) на \(e^{j ω t}\) , взяв действительную часть результата \( V( t ) = Re(\mathbf{V}e^{j ω t}) \) , ну, и подставив t, куда ж без этого.
В электротехнике комплексные числа записываются с использованием буквы «j» , вместо «i» , чтобы не путать последнюю с обозначением малого изменения тока. Таким образом, в общем случае актуальная величина напряжения и тока выражается как \[ \begin{align} V( t ) &=\mathscr{Re}[\mathbf{V}e^{j ω t}] \\ &=\mathscr{Re}[\mathbf{V}\cos( ω t ) + j\mathbf{V}\sin( ω t )] \\ &=\mathbf{V}\cos( ω t ) \\ \\ I( t ) &=\mathscr{Re}[\mathbf{I}e^{j ω t}] \\ &=\mathscr{Re}[\mathbf{I}\cos( ω t ) + j\mathbf{I}\sin( ω t )] \\ &=\mathbf{I}\cos( ω t ) . \end{align} \]
Конец переписанного абзаца.
Например, напряжение, выраженное комплексным числом \(\mathbf{V}=5j\) , соответствует напряжению, описываемому выражением \[ V( t ) = \mathscr{Re}[(5j)\cos( ω t ) + (5j) j\sin( ω t )] = –5\sin( ω t ) \] вольт.
[* Люблю такое: «очевидно, что» и гиперпространственный прыжок на пару парсеков вперёд. А косинус куда девался?
Начнём с того, что полная форма выглядит так: \(\mathbf{V}=0+5j\), т.е. вектор сонаправлен с осью Im , она же oY . Если бы множитель при действительной части был ненулевой, пришлось бы заниматься умножением многочленов (a + jb)(c + jd) , которое так любят все, изучающие ТОЭ.
Операция \(\mathscr{Re}\) извлекает из выражения только действительную ( \(Re\) ) часть от комплEксного представления \( V( t )\) , т.е. ту, в которую НЕ входит сомножителем «корень из минус единицы», и передаёт её на выход в неизменном виде. ( Сходным образом действует операция «модуль числа», которая просто отбрасывает знак ). Иначе говоря, полный вывод:
\[
\begin{align}
V( t ) &= \mathscr{Re}[(5j)\{\space\cos( ω t ) + j\sin( ω t )\space\}] \\
&= \mathscr{Re}[(5j)\cos( ω t ) + (5j) j\sin( ω t )] \\
&= \mathscr{Re}[(5j)\cos( ω t ) + (5j\space^2 )\sin( ω t )] \\
&= \mathscr{Re}[(5j)\cos( ω t ) + (5(\sqrt{-1})^2 )\sin( ω t )] \\
&= \mathscr{Re}[(5j)\cos( ω t ) + (-5)\sin( ω t )] \\
&= \space –5\sin( ω t ) .
\end{align}
\] ]
1.7.4 Реактивное сопротивление конденсатора и катушки
В соответствии с обозначенными правилами можно корректно применять обобщённый закон Ома к конденсаторам и катушкам в той же степени, что и к резисторам, если известно реактивное сопротивление ёмкости или индуктивности. Посмотрим, как это делается. Начнём с простого синусоидального напряжения \( V_0\cos( ω t) \) , приложенного к конденсатору. \[ V( t )=\mathscr{Re}( V_0e^{j ω t}). \]
Зная выражение для тока \(I = C( dV/dt )\) , получаем \[ I( t )=\mathscr{Re}\left(\cfrac{V_0e^{j ω t}}{-\cfrac{j}{ ω C}}\right ) = \mathscr{Re}\left(\frac{V_0e^{j ω t}}{Z_C}\right ) \]
[*
\[
\begin{align}
I( t )=&\text{(1)}= \mathscr{Re}[C( dV( t )/dt )]= \mathscr{Re}\left[C\frac{dV( t )}{dt}\right]= \mathscr{Re}\left[C\frac{d}{dt}V( t )\right]= \\
&\text{(2)}= \mathscr{Re}\left[C\frac{d}{dt}[V_0e^{j ω t}\space]\right]= \\
&\text{(3)}= \mathscr{Re}\left[CV_0\frac{d}{dt}[e^{j ω t}\space]\right]= \\
&\text{(4)}= \mathscr{Re}\left[CV_0(jω)[e^{j ω t}\space]\right]= \\
&\text{(5)}= \mathscr{Re}\left[\frac{j}{j}CV_0(jω)[e^{j ω t}\space]\right]= \mathscr{Re}\left[\frac{j\space^2ωCV_0[e^{j ω t}\space]}{j}\right]= \mathscr{Re}\left[\frac{ωCV_0[e^{j ω t}\space]}{-j}\right]=\mathscr{Re}\left[\cfrac{V_0e^{j ω t}}{-\cfrac{j}{ ω C}}\right]= \\
&\text{(6)}= \mathscr{Re}\left[\frac{V_0e^{j ω t}}{Z_C}\right]
\end{align}
\]
(1) Форматируем
(2) Подстановляем \(V( t )\)
(3) Выносим из-под дифференциала независящий от \(t\) постоянный множитель \(V_0\) ( см. таблицу производных §A.3.1 )
(4) Дифференцируем сложную функцию \(e^{j ω t}\) ( см. таблицу производных §A.3.1 )
(5) Тривиальные преобразования
(6) Результат
Очевидно, чё. Кто бы спорил ].
т.е. для конденсатора \[ \mathbf{Z_C}=\frac{-j}{ ω C} = -jX_C \] \(\mathbf{Z_C}\) - импеданс конденсатора на частоте \(ω\) . По модулю он равен реактивному сопротивлению \( X_C=1/( ω C ) \) , полученному ранее, но имеет множитель «–j», который указывает на то, что ток опережает по фазе напряжение на 90° . Например, конденсатора 1 μF имеет импеданс —2653 jΩ на 60 Hz и —0.16 jΩ на 1 MHz 41 . Его реактивное сопротивление ( и импеданс ) бесконечен на постоянном токе.
Аналогичный вывод для катушки даёт \[ \mathbf{Z_L} = j ω L = jX_L. \]
Схема, содержащая только конденсаторы и катушки, всегда имеет чисто мнимый импеданс, т.е. токи и напряжения в схеме всегда имеют разницу фаз 90° , т.е. чисто реактивные. Если в схеме есть резистор, то возникает действительная часть импеданса. В этом случае термин «реактивное» относится только к мнимой части.
[* Ток в конденсаторе опережает по фазе напряжение, значит, сначала в конденсаторе появляется ток, который изменяет напряжение на обкладках. Ток отстаёт от напряжения, значит, сначала к катушке прикладывается напряжение, а затем в ней начинает течь ток ].
==46
1.7.5 Обобщённый закон Ома
Соглашения по представлению напряжений и токов упрощает форму закона Ома: \[ \begin{align} \mathbf{I} &= \mathbf{V/Z}, \\ \mathbf{V} &= \mathbf{I×Z}, \end{align} \] где напряжение \(\mathbf{V}\) прикладывается к импедансу \(\mathbf{Z}\) вызывая появление тока \(\mathbf{I}\) . Комплексные импедансы при последовательном и параллельном соединении подчиняются тем же правилам, что и сопротивление. \[ \mathbf{Z= Z_1 + Z_2 +...} \qquad [1.30] \] \[ \mathbf{Z=\cfrac{1}{\cfrac{1}{Z_1}+\cfrac{1}{Z_2}+...}} \qquad [1.31] \]
Наконец, для полноты изложения дополним всё это формулами импедансов резистора, конденсатора и катушки:
\[ \begin{align} \mathbf{Z_R} &= R &\text{( resistor )}, \qquad \qquad \quad \space \\ \mathbf{Z_C} &= \frac{–j}{ω C}= \frac{1}{j ω C} \qquad &\text{( capacitor )}, \qquad [1.32] \\ \mathbf{Z_L} &= j ω L &\text{( inductor )}. \qquad \qquad \quad \end{align} \]Используя этот набор можно анализировать схемы на переменном токе, используя те же методы, что и на постоянном токе, скажем, формулы последовательного и параллельного соединения. Результаты для делителя напряжения будут выглядеть так же, как раньше. Для множественных соединений, как и на постоянном токе, работают законы Кирхгоффа, просто на этот раз надо использовать комплексные представления для напряжений и токов, а именно: сумма падений напряжений в замкнутом контуре равна нулю, и сумма токов в узле равна нулю. Последнее правило означает, что, переменный ток, как и постоянный, в любой точке последовательного соединения одинаков.
Упражнение 1.25
Используя изложенные правила для последовательного и параллельного соединения, выведите формулы [1.17] и [1.18] для ёмкости двух конденсаторов
(a) при параллельном и
(b) при последовательном соединении.
Подсказка . В каждом случае выпишите импедансы для требуемого соединения, приравняйте к импедансу эквивалентной ёмкости, подставьте импедансы конденсаторов и найдите эквивалентную ёмкость.
Применим описанный метод к самой простой схеме переменного тока - переменному напряжению, приложенному к конденсатору, которая рассматривалась в §1.7.1 . Затем, после краткого знакомства с мощностью в реактивных цепях ( чтобы закончить с базовыми сведениями ), проанализируем ( на этот раз правильно ) простые, но очень важные и полезные RC фильтры низких и высоких частот.
Предположим, что конденсатор 1 μF подключён к сети 115 Vrms@60 Hz . Какой ток течёт через конденсатор? Используя обобщённый закон Ома, имеем: \[ \mathbf{Z} = - \frac{j}{ω C}. \] Ток выражается \[ \mathbf{I = V/Z}. \]
Так как фаза может быть любой, выбираем \(\mathbf{V}\)=A , т.е. \( V( t )=A\cos( ω t) \) , где A=115\(\sqrt2\)=163V . Тогда: \[ \mathbf{I} = j ω CA ≈ –0.061 \sin( ω t ). \]
Ток имеет амплитуду 61 mA (43 mArms) и опережает напряжение на 90° , что согласуется с предыдущими выкладками. Можно заметить, что импеданс конденсатора отрицательный и мнимый , поэтому, независимо от фазы \( V \) , фаза тока через конденсатор \(I_{cap}\) должна опережать его на 90° . В общем случае угол между током и напряжением для любой двухвыводной схемы из резисторов, конденсаторов и катушек, эквивалентен углу импеданса этой схемы [* между вектором импеданса и осью Re (0X) ] .
[*
Повторим расчёты в развёрнутом виде.
Конденсатор 1 μF имеет на 60 Hz импеданс –2653 jΩ . По обобщённому закону Ома \( \mathbf{I} = \mathbf{V/Z} \). Тогда
Длина вектора тока \( | \mathbf{I} | \) составит: 163V/(–2653 jΩ) = –0.06143987938183188·j [V/Ω]
Собираем всё вместе
\[
\begin{align}
I(t)&=\mathscr{Re}\left[–0.06143987938183188·j·\{\space\cos( ω t ) + j\sin( ω t )\space\}\right] \\
&=\mathscr{Re}\left[–0.06143987938183188·\{\space j\cos( ω t ) + j\space^2\sin( ω t )\space\}\right] \\
&=\mathscr{Re}\left[–0.06143987938183188·\{\space j\cos( ω t ) - \sin( ω t )\space\}\right] \\
&=\space –0.06143987938183188·\{ - \sin( ω t )\space\} \qquad [V/Ω]
\end{align}
\]
Со знаком нахомутал где-то. Но в главном-то всё правильно.... ]
[* Ещё раз. Отрицательный импеданс означает, что НЕ напряжение, приложенное к импедансу, вызывает появление тока в цепи, но ток приложенный к импедансу вызывает появление в цепи потенциала. Т.е. знак импеданса означает ответ на вопрос «кто на ком стоял?». Если положительный, то как в резисторе, если отрицательный, то как в конденсаторе ].
Отметим, что если нужна только величина тока и не интересует разница фаз, можно было бы обойтись без действий с комплексными числами: если \(\mathbf{A=B/C}\) , то A=B/C
где A, B и C - модули соответствующих комплексных величин. Это позволяет обойтись без умножения ( см. также упражнение 1.18 ). Таким образом, \[ I = V/Z = ω CV. \]
Этот приём уже использовался ранее ( потому что авторы ничего лучше не знают ) и часто бывает полезен.
Конденсатор из примера не рассеивает мощность и не увеличит счёт за электричество, что будет ясно из следующего параграфа. Затем рассмотрим схемы из резистора и конденсатора с помощью обобщённого закона Ома.
Упражнение 1.26
Покажите, что, если \(\mathbf{A=BC}\) , то A=BC , где A, B и C - модули комплексных чисел \(\mathbf{A,B}\) и \(\mathbf{C}\) .
Подсказка . Представьте каждое комплексное число в показательной форме \(\mathbf{A}\)=A\(e^{j θ }\) .
==46
36 Модуль [* длина вектора ] \(\mathbf{Z}\) даёт отношение амплитуд напряжения и тока, а угол между направлением \(\mathbf{Z}\) и направлением оси «X» сообщает разницу фаз между током и напряжением. <-
37 Позднее будет рассматриваться катушка индуктивности , у которой тоже есть разница фаз 90° , но противоположного знака. Она характеризуется реактивным сопротивлением \(X_L\) . <-
38 Потому что по нему нельзя понять какую величину имеет сдвиг фаз. Фаза выходного напряжения на высоких частотах опережает вход на 90° , на низких равна 0° , а значение 45° имеет на частоте \(ω_0\) , см. рис. 1.104 в §1.7.9 . <-
39 Есть два важных исключения: согласованные линии передачи и источники тока. <-
40 Использование тока а не напряжения облегчает здесь расчёты. В итоге получаем простую производную вместо простого интеграла. <-
41 Обращаем внимание, что по соглашению реактивное сопротивление \(X_C\) - действительное число ( разница фаз 90° закодирована словом «реактивное» ) но соответствующий импеданс является чисто мнимым \(\mathbf{Z}=0-jX_C\) . <-

