Приложение E. LC фильтры Баттерворта

==1109

Активные фильтры ( см. Часть _6 ) очень удобны на низких частотах, но совершенно непрактичны на радиочастотах из-за высоких требований к скорости нарастания и полосе используемых операционных усилителей. На частотах выше 100 kHz ( а часто и на более низких ) наилучшим решением будут фильтры на конденсаторах и катушках индуктивности. На сверхвысоких частотах ( UHF ) и в микроволновом диапазоне фильтры на сосредоточенных элементах [* т.е. геометрические размеры элементов фильтра малы по сравнению с длиной волны сигнала ] заменяют на конструкции с микрополосковыми линиями и резонаторами.

Как и в случае активных фильтров, есть много подходов к выбору параметров при построении LC схем. Можно собрать классические фильтры Баттерворта, Бесселя и Чебышева во всех возможных конфигурациях - ФНЧ, ФВЧ, полосовой и заграждающей. Проще всего строить фильтры Баттерворта, для которых на паре страниц можно описать базовые расчётные параметры для ФНЧ и ФВЧ и даже привести несколько примеров.

E.1 Фильтр низкой частоты

В табл. E.1 собраны нормализованные величины индуктивностей и емкостей для ФНЧ разных порядков. Номиналы для рабочей схемы вычисляются по правилам масштабирования импедансов \[ \begin{align*} L_n(actual) &= \frac{R_LL_n(table)}{ω} , \\ C_n(actual) &= \frac{C_n(table)}{ωR_L} , \end{align*} \]

где \(R_L\) - импеданс нагрузки, а \(ω\) - круговая частота среза \(ω = 2πf\) .

Значения в табл. E.1 даются для двух наиболее распространённых случаев, а именно:

для равных импедансов источника и нагрузки и
для случая большой разницы импедансов на разных сторонах ( в обоих вариантах ).

Расчёт начинают с выбора порядка фильтра по АЧХ фильтра Баттерворта ( рис. 6.30 ). Затем выбирается конфигурация фильтра ( T- или π-, см. рис. E.1 ) и номиналы компонентов. Для одинаковых импедансов на входе и выходе подходят оба варианта, но в π- будет меньше индуктивностей. Если импеданс нагрузки много больше импеданса источника нужна T-конфигурация, если же он наоборот много меньше - π-конфигурация.

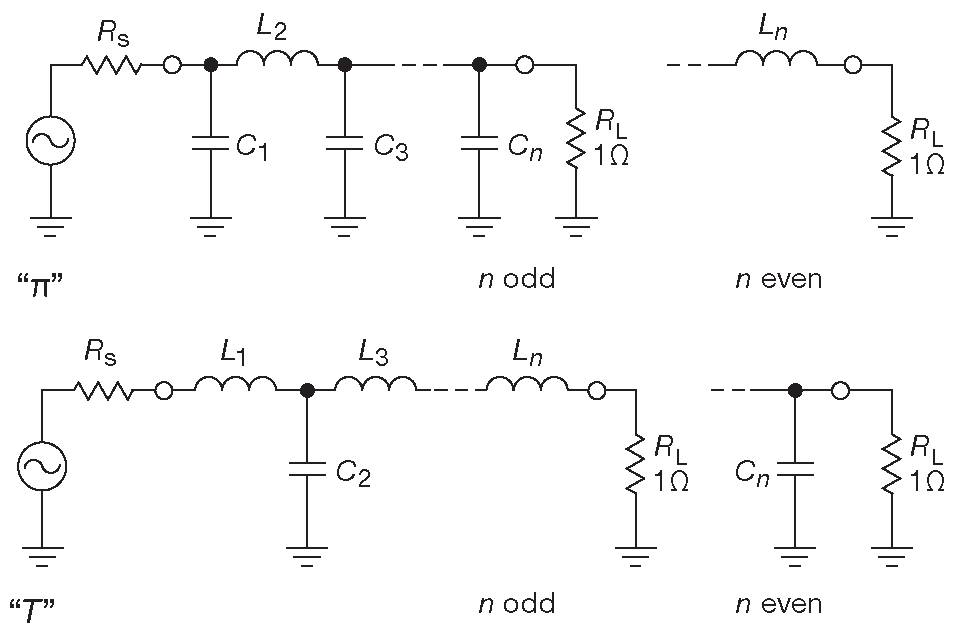
Рис. E.1 π- и T-конфигурации, см. табл. E.1 и текст

E.2 Фильтр высоких частот

При расчёте ФВЧ, как и ранее, выбирается порядок и конфигурация, затем проводится универсальное преобразование ФНЧ в ФВЧ ( рис. E.2 ). В данном случае индуктивности просто меняются на ёмкости и наоборот. Рабочие номиналы получаются из нормализованных значений из табл. E.1 по следующим правилам масштабирования импедансов:

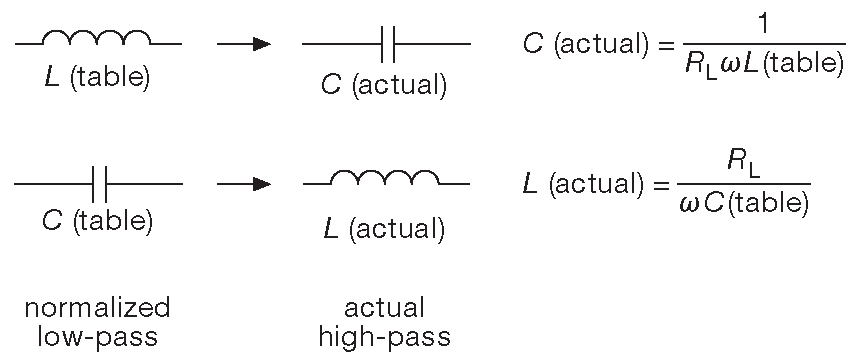
Рис. E.2 Преобразование ФНЧ в ФВЧ

\[ \begin{align*} L_n(actual) &= \frac{R_L}{ωC_n(table)} , \\ C_n(actual) &= \frac{1}{R_LωL_n(table)} . \end{align*} \]

E.3 Примеры фильтров

Приведём несколько примеров, раскрывающих процедуру расчёта.

Пример 1: Требуется рассчитать фильтр нижних частот пятого порядка для импеданса источника и нагрузки 75 Ω и частоты среза «-3dB» 1 MHz .

==1110

Будем использовать π-конфигурацию, чтобы минимизировать число катушек индуктивности. Правила масштабирования дают: \[ \begin{align*} C_1=C_5 &= \frac{0.618}{2π×10\space^6×75} &= 1310pF , \\ L_2=L_4 &= \frac{75×1.618}{2π×10\space^6} &= 19.3μH , \\ C_3 &= \frac{2}{2π×10\space^6×75} &= 4240pF . \end{align*} \] Финальная схема показана на рис. E.3 . Отметим, что все фильтры с одинаковыми импедансами источника и приёмника имеют симметричную конструкцию.

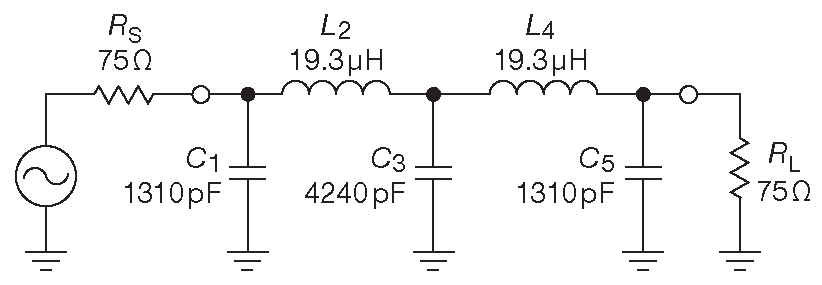
Рис. E.3 Схема из Примера 1 . ФНЧ пятого порядка со срезом 1 MHz и одинаковыми импедансами на входе и выходе

Пример 2

Нужен фильтр нижних частот для импеданса источника 50 Ω , приёмника 10 kΩ и частотой среза 100 kHz .

\(R_S ≪ R_L\) , поэтому выбираем T-конфигурацию. Для \(R_L\) правила масштабирования дают:

\[ \begin{align*} L_1 &= \frac{10\space^4×1.5}{2π×10\space^5} &= &23.9mH , \\ C_2 &= \frac{1.3333}{2π×10\space^5×10\space^4} &= &212pF , \\ L_3 &= \frac{10\space^4×0.5}{2π×10\space^5} &= &7.96mH . \end{align*} \] Законченный фильтр показан на рис. E.4 .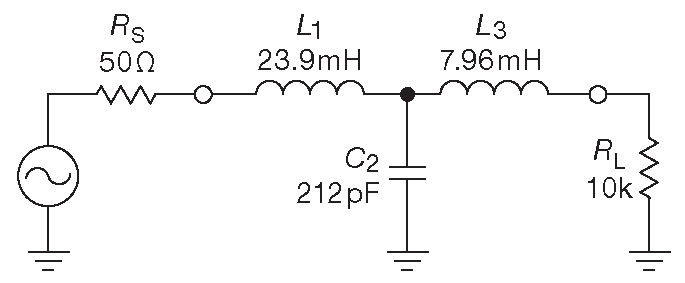

Рис. E.4 Схема для Примера 2 . ФНЧ третьего порядка со срезом 100 kHz , источником 50Ω и нагрузкой 10 kΩ

Пример 3

Требуется ФНЧ четвёртого порядка для нулевого импеданса источника ( источник напряжения ), нагрузки 75 Ω и частоты среза 10 MHz .

Как и в предыдущем примере, используем T-конфигурацию, потому что R_S ≪R_L . Правила масштабирования дают:

\[ \begin{align*} L_1 &= \frac{75×1.5307}{2π×10\space^7} &= &1.83μH , \\ C_2 &= \frac{1.5772}{2π×10\space^7×75} &= &335pF , \\ L_3 &= \frac{75×1.0824}{2π×10\space^7} &= &1.29μH , \\ C_4 &= \frac{0.3827}{2π×10\space^7×75} &= &81.2pF . \end{align*} \] Законченный фильтр показан на рис. E.5 .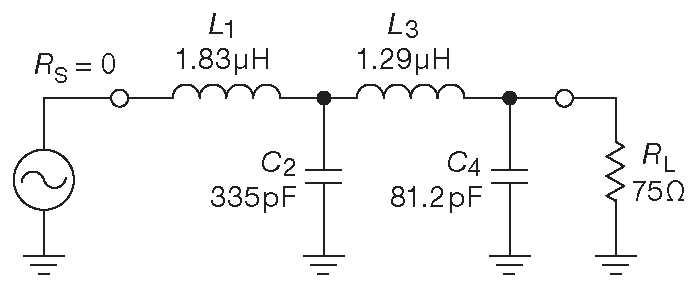

Рис. E.5 Схема для Примера 3 . ФНЧ четвёртого порядка со срезом 10 MHz , источником напряжения и нагрузкой 75Ω

Table E.1 Butterworth Lowpass Filters3

n *- Rs Ci L2 C3 L4 C5 L6 C7 L8 T >~1/Rs Li C2 L3 C4 L5 C6 L7 C8 n = 2 { 1 ro 1.4142 1.4142 1.4142 0.7071 n = 3 { 1 ro 1.0000 2.0000 1.0000 1.5000 1.3333 0.5000 n = 4 { 1 ro 0.7654 1.8478 1.8478 0.7654 1.5307 1.5772 1.0824 0.3827 n = 5 { 1 ro 0.6180 1.6180 2.0000 1.6180 0.6180 1.5451 1.6944 1.3820 0.8944 0.3090 n = 6 { 1 ro 0.5176 1.4142 1.9319 1.9319 1.4142 0.5176 1.5529 1.7593 1.5529 1.2016 0.7579 0.2588 n = 7 { 1 ro 0.4450 1.2470 1.8019 2.0000 1.8019 1.2470 0.4450 1.5576 1.7988 1.6588 1.3972 1.0550 0.6560 0.2225 n = 8 { 1 ro 0.3902 1.1111 1.6629 1.9616 1.9616 1.6629 1.1111 0.3902 1.5607 1.8246 1.7287 1.5283 1.2588 0.9371 0.5776 0.1951 Notes: (a) Values of Ln, Cn for 10 load resistance, and cutoff frequency (-3dB) of 1 rad/s. See text for scaling rules.

==1111

Пример 4

Требуется разработать ФНЧ второго порядка для источника тока на входе и нагрузки 1 kΩ со срезом 10 kHz .

\(R_S ≫ R_L\) , поэтому используем π-конфигурацию. Правила масштабирования дают: \[ \begin{align*} C_1 &= \frac{1.4142}{2π×10\space^4×10\space^3} &= &0.0225μF , \\ L_2 &= \frac{10\space^3×0.7071}{2π×10\space^4} &= &11.3mH . \end{align*} \] Схема фильтра приводится на рис. E.6 .

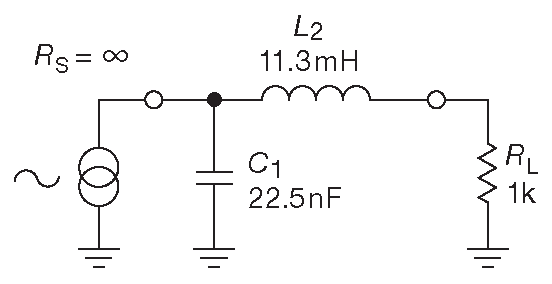
Рис. E.6 Схема для Примера 4 . ФНЧ второго порядка со срезом 10 kHz , источником тока и нагрузкой 1 kΩ

Пример 5

Требуется фильтр высоких частот третьего порядка для импедансов 52 Ω на входе и выходе и срезом 6 MHz .

Начинаем с T-конфигурации, затем проводим трансформацию катушек индуктивности в конденсаторы и наоборот. Получаем:

\[ \begin{align*} C_1=C_3 &= \frac{1}{52×2π×6×10\space^6×1.0} &= &510pF , \\ L_2 &= \frac{52}{2π×6×10\space^6×2.2} &= &0.690μH . \end{align*} \] Итоговая схема показана на рис. E.7 .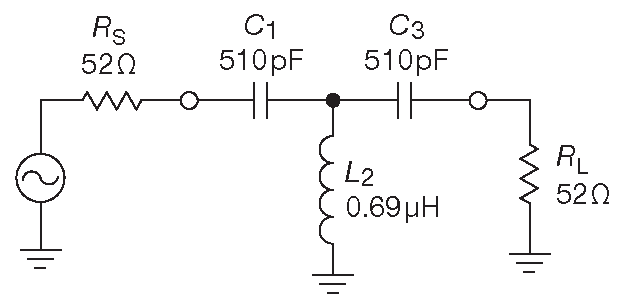

Рис. E.7 Схема для Примера 5 . ФВЧ третьего порядка со срезом 6 MHz и равными импедансами на входе и выходе

Хотелось бы подчеркнуть, что тема разработки пассивных фильтров столь богата, что эта маленькая таблица и материал приложения даже не начал царапать её поверхность.

==1111