6.3 (I) Схемы фильтров

==406

Масса труда и таланта была потрачена на создание схем активных фильтров, каждая из которых используется для реализации того или иного типа фильтров. Может возникнуть вопрос, зачем нужно более одной реализации, скажем, фильтра Бесселя? Причина в том, что конкретная схема может вытянуть только один из требуемых параметров, универсального решения, закрывающего все вопросы нет.

Активные фильтры можно собирать на дискретных компонентах с ОУ в качестве активного элемента ²⁴. В этом случае придётся подобрать резисторы и конденсаторы, которые и зададут нужные параметры. Чем точнее задаются требования по частоте, тем жёстче должен быть допуск пассивных компонентов и стабильнее их параметры. Привлекательной альтернативой могут служить специализированные ИМС активных фильтров, большая часть соединений в которых уже сделана внутри корпуса, и часто уже имеются некоторые согласованные пассивные компоненты.

Есть два базовых класса активных фильтров: «фильтры непрерывного времени» и фильтры «на переключаемом конденсаторе» [* т.е. «дискретного времени»] . Фильтры непрерывного времени - аналоговые устройства, собранные на ОУ, резисторах и конденсаторах. Параметры фильтра устанавливаются номиналами компонентов и их межсоединениями. Фильтры на переключаемом конденсаторе используют конденсаторы и МОП ключи, замыкаемые и размыкаемые синхронно с внешним тактовым сигналом, и замещают ими входные резисторы в схеме классического интегратора. Номинал «резистора» устанавливается частотой тактирования. Типичный фильтр на переключаемых конденсаторах использует несколько таких интеграторов в связке с дополнительными ОУ, чтобы реализовать заданную функцию ²⁵. Преимуществом фильтров на переключаемом конденсаторе является перестройка параметров в широком диапазоне за счёт простого изменения частоты тактирования, стабильность параметров и относительно несложная реализация в интегральном исполнении. Но такие фильтры больше шумят ( т.е. их динамический диапазон уже ), имеют больший уровень искажений и могут вносить в сигнал артефакты, свойственные переключаемым схемам: появление фантомных сигналов и проникание тактовой частоты в аналоговый тракт.

==407

Обычно от активных фильтров хотят:

небольшого числа компонентов как активных, так и пассивных;
простоты настройки;
малого числа номиналов, особенно для конденсаторов;
отсутствия чрезмерных требований к операционным усилителям ( к скорости нарастания, полосе пропускания и выходному импедансу );
способности создавать высокодобротные фильтры;
электронную перестройку;
нечувствительность параметров к величинам компонентов и усилению ОУ ( особенно к произведению усиления на полосу [* GBW ] или $ f_T $ ) .

В большинстве случаев последнее свойство самое важное. Схема, требующая точных компонентов, сложна в настройке, и её параметры будут плыть по мере старения компонентов. Наибольшую популярность получила конфигурация VCVS за простоту и небольшое число деталей, но она как раз чувствительна к их допуску. В последнее время интерес смещается к более сложным схемам, которые спокойнее относятся к некоторому разбросу номиналов.

В этой главе представляются несколько схем для ФНЧ, ФВЧ и полосовых фильтров. Знакомство начнётся с популярных VCVS, затем последуют фильтры с изменяемыми параметрами, выпускаемыми в виде законченных ИМС несколькими фирмами, и в конце будет рассмотрен фильтр-пробка «двойной-Т» конфигурации.

Большая часть современных микросхем активных фильтров относятся к схемам с переключаемым конденсатором, т.к. такой вариант архитектуры прост в использовании, компактен, дёшев, имеет отменную стабильность и ( иногда ) совсем не нуждается во внешних компонентах. Эти микросхемы будут рассмотрены в конце данной части.

6.3.1 VCVS схемы

Источники напряжения, управляемые напряжением ( VCVS ) или фильтры с контролируемым источником , были изобретены Салленом и Ки ( в книге они появились в §6.2.4.E [* на самом деле в §4.3.6 ] ). Это вариант простого устройства с единичным усилением, показанного ранее на рис. 6.16 . В VCVS повторитель заменяется неинвертирующим каскадом с отличным от единицы усилением. На рис. 6.28 показаны варианты для ФНЧ, ФВЧ и полосового фильтра. Резисторы на выходе ОУ служат для задания усиления K , а остальные элементы отвечают за АЧХ схемы. На рисунке изображены 2-полюсные фильтры, которые могут быть и фильтрами Баттерворта, и Бесселя, и др. Тип зависит только от номиналов компонентов, что будет показано далее. Для получения фильтров более высокого порядка можно каскадировать любое число 2-полюсных секций VCVS, причём все секции общего набора будут различаться между собой. Каждая получит собственный квадратичный коэффициент полинома n-ного порядка, описывающего требуемый фильтр.

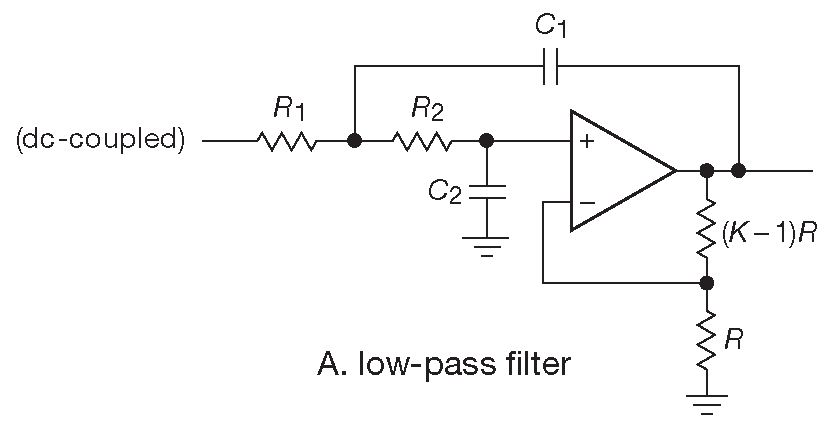
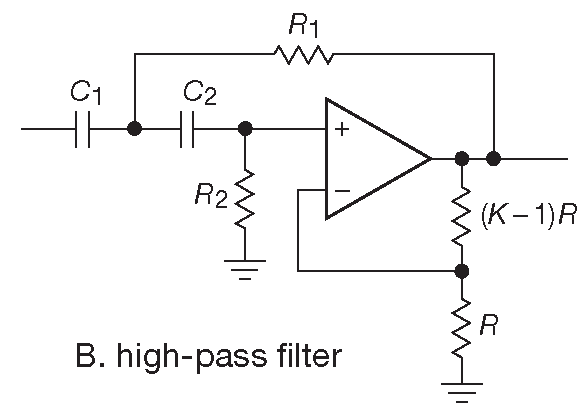
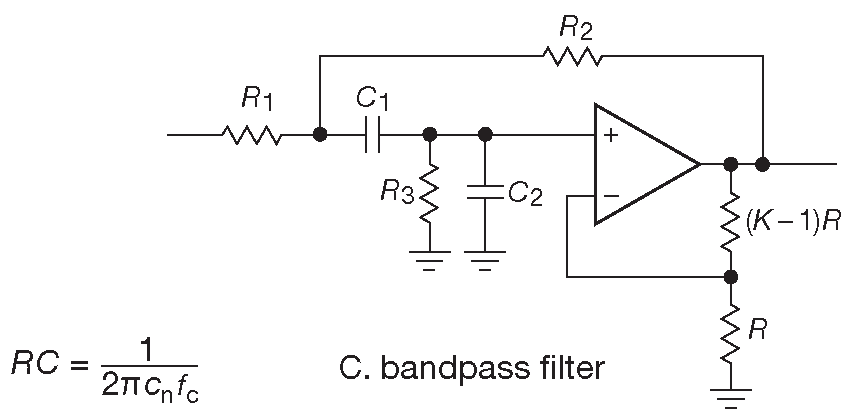
Рис. 6.28 Активные фильтры архитектуры VCVS

В большинстве специализированных справочников есть уравнения и таблицы коэффициентов для всех стандартных типов и отдельный набор таблиц для каждого значения неравномерности в фильтре Чебышева. В следующем параграфе имеется удобная таблица коэффициентов VCVS для фильтров Баттерворта, Бесселя и Чебышева ( для последнего с пульсациями 0.5 dB и 2 dB в полосе пропускания ), пригодная для построения ФНЧ и ФВЧ. Полосовые пропускающие и заграждающие фильтры комбинируются из двух указанных.

6.3.2 Разработка VCVS фильтров по упрощённой таблице

Для начала надо понять, что именно предполагается получить в итоге. Как говорилось ранее, «Баттерворт» следует рассматривать, если требуется максимально плоская АЧХ в рабочей полосе, «Чебышев» даёт самый резкий переход к заграждению ( ценой увеличения пульсаций в полосе пропускания ), а «Бессель» имеет наилучшие фазовые характеристики, т.е. постоянное время задержки в полосе пропускания и, соответственно, хорошую реакцию на перепад. Частотные характеристики для каждого типа приводятся на рис. 6.30 .

==408

Чтобы собрать n-полюсный фильтр ( для чётного n ) требуется соединить последовательно n/2 VCVS секций. В каждой секции $R_1=R_2=R$ и $ C_1=C_2=C$ . Для схем на типовых ОУ $R$ выбирается из диапазона от 10 kΩ до 100 kΩ . Низкоомных номиналов следует избегать, т.к. выходной импеданс ОУ без обратной связи на высоких частотах растёт, и его придётся учитывать в вычислениях. А дальше нужно только задать коэффициенты усиления K каждого каскада в соответствии с данными таблицы. Для фильтра порядка n есть n/2 значений, каждое - для отдельной секции.

Table 6.2 VCVS Lowpass Filters

6.3.2.A Фильтры нижних частот Баттерворта

Для фильтра Баттерворта резисторы и конденсаторы всех секций имеют одинаковые номиналы и должны соответствовать соотношению $RC=q/( 2πf_c ) $ , где $ f_c$ требуемая частота «-3dB» фильтра. Скажем, чтобы сделать фильтр 6-го порядка, надо включить последовательно три VCVS секции с усилениями 1.07, 1.59, 2.48 и одинаковыми величинами $R$ и $ C $ для требуемой частоты «-3dB». Желательно выставлять коэффициенты усиления именно в указанном порядке, чтобы избежать проблем с динамическим диапазоном [* в цифровых фильтрах речь бы шла о проблемах с переполнением разрядной сетки при математических операциях] .

6.3.2.B Фильтры нижних частот Бесселя и Чебышева

Для фильтров Бесселя и Чебышева процесс чуть более замысловатый. Здесь тоже используются секции 2-го порядка со своим усилением в каждой секции. Внутри секции $R_1=R_2=R$ и $ C_1=C_2=C$ , но, в отличие от «Баттерворта», каждая секция «Бесселя» и «Чебышева» имеет своё произведение $RC$ , которое должно масштабироваться с коэффициентом $ c_n$ из табл. 6.2 по формуле $RC=1/( 2πc_nf_c ) $ , где $ f_c$ для «Бесселя» - точка «-3dB», а для «Чебышева» - конец полосы пропускания, т.е. место, где АЧХ выходит из допустимого коридора неравномерности в полосе пропускания и начинает движение к полосе заграждения. Например, для «Чебышева» с неравномерностью 0.5 dB и $ f_c$=100 Hz пульсации будут иметь величину от +0 до –0.5 dB , а дальше по частоте уровень ослабления начнёт резко расти. В таблице есть цифры для «Чебышева» с неравномерностью 0.5 и 2.0 dB . У последнего переход к заграждению чуть резче ( рис. 6.30 ).

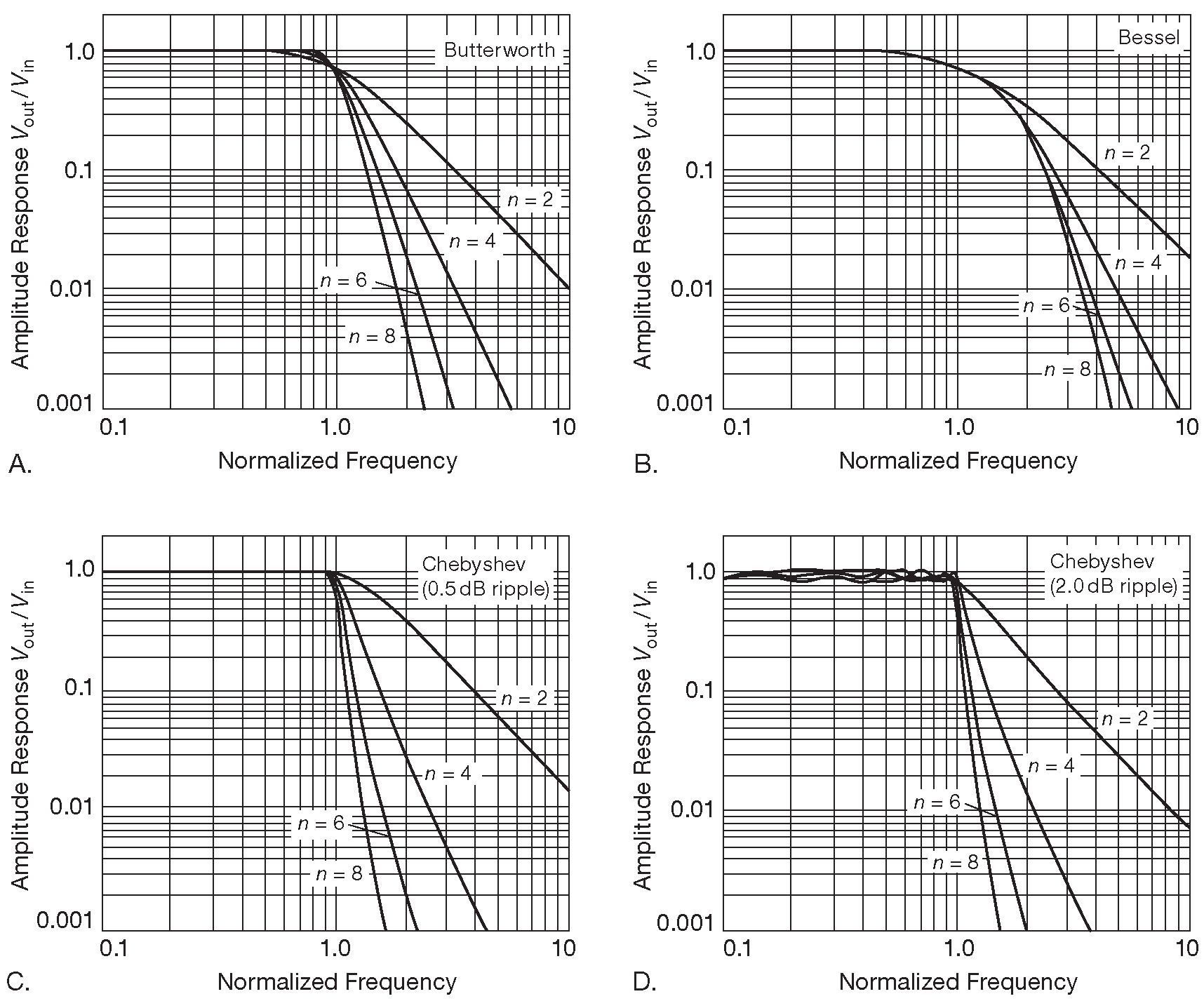
Рис. 6.30 Нормализированные АЧХ для фильтров 2-, 4-, 6- и 8-го порядков по данным из табл. 6.2 . Фильтры Баттерворта и Бесселя нормированы по уровню «-3dB» на единичной частоте, а «Чебышев» - по уровню подавления 0.5 и 2.0 dB . Как и раньше, верхняя граница пульсаций в полосе пропускания принята за единицу

Пример

В качестве иллюстрации на рис. 6.29 показан VCVS фильтр 4-го порядка с $ f_c$=100 Hz . В таблице перечислены номиналы резисторов для трёх типов фильтров, рассчитанные по приведённой методике. Аналогичный фильтр Баттерворта 6-го порядка с $ f_c$=90 Hz использовался для создания синусоидального напряжения из прямоугольного сигнала, полученного от кварцевого генератора. Выходное синусоидальное напряжение шло на привод телескопа ²⁶.

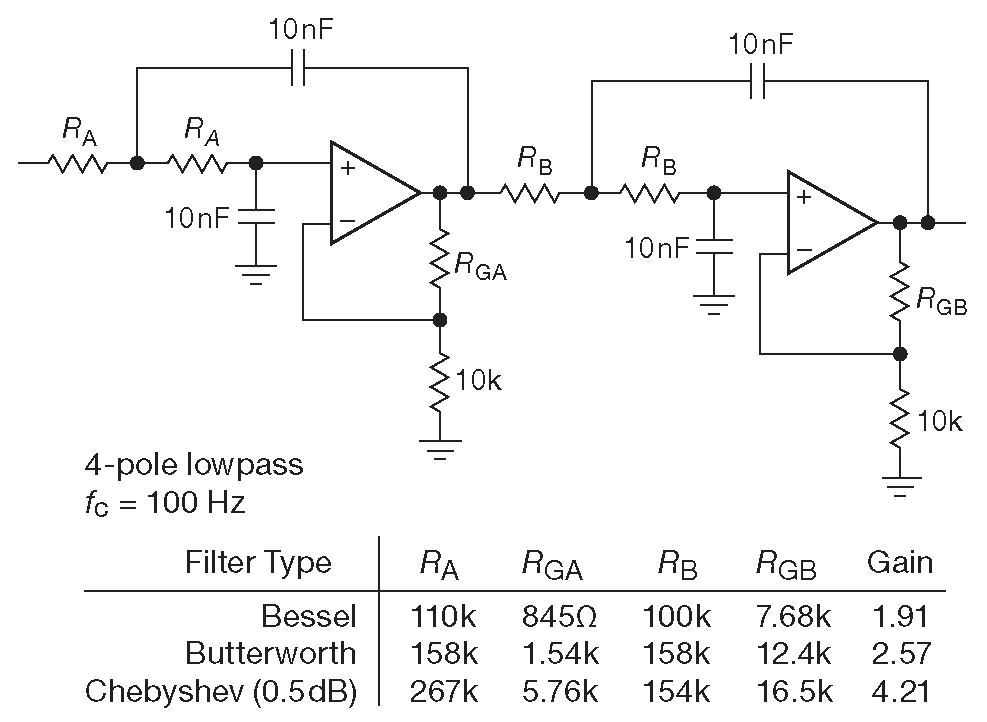
Рис. 6.29 Пример VCVS фильтра. Для резисторов выбрано ближайшее стандартное значения из 1%-набора номиналов «E96»

6.3.2.C Фильтры высоких частот

Для фильтров высоких частот надо собирать VCVS схему в конфигурации ФВЧ, т.е. поменять местами резисторы и конденсаторы. Для «Баттерворта» схема расчёта не меняется ( то же значение K , так же считаются величины $R$ и $ C $ ) . Для «Бесселя» и «Чебышева» K не меняется, а нормирующий множитель $ c_n$ должен использоваться в виде обратной величины, т.е. «новое значение $ c_n$» равно ( 1/«табличное $ c_n$» ).

==409

Полосовые пропускающие фильтры строятся каскадированием ФНЧ и ФВЧ с перекрывающимися рабочими полосами, а полосовые заграждающие из фильтров с неперекрывающимися полосами. Но такие составные фильтры не могут иметь высокую добротность ( очень острую характеристику в полосе пропускания ), т.к. весьма чувствительны к номиналам компонентов каждой исходной секции. Для высокодобротных фильтров надо использовать специальную VCVS схему, показанную ранее, или описываемые в следующей главе биквадратные и фильтры с изменяемыми параметрами. Такие схемы даже в 2-полюсном варианте способны формировать АЧХ с очень острым пиком. Дополнительные подробности по теме можно найти в стандартных источниках.

6.3.2.D Обобщение фильтров Саллена-Ки

Упрощение конструкции фильтров по схеме Саллена-Ки ( или VCVS ) происходит за счёт использования в каждой секции одинаковых номиналов резисторов и конденсаторов, но это упрощение уравновешивается различными и неудобными коэффициентами усиления каскадов ( колонка «Gain» на рис. 6.29 ).

Часто требуется прямо задать коэффициент усиления, чтобы предотвратить насыщение, или, наоборот, изменить параметры фильтра, не трогая усиление. Ужесточая требования к усилению, надо ослаблять ограничения по номиналам R и C. С подробностями по данной теме можно ознакомиться в парочке хороших заметок по применению от Джеймса Карки ( James Karki ) из TI ²⁷. Подытоживая, можно сказать, что можно создать фильтр с любыми характеристиками, используя каскады с заданным усилением, если есть возможность свободного выбора номиналов пассивных компонентов.

==410

Согласно алгоритму Карки, можно записать общие формулы для частоты среза $ f_c$ и добротности Q 2-полюсной секции Саллена-Ки, в которой отношения компонентов будут иметь любое значение. Следуя обозначениям ²⁸ на рис. 6.28A определим параметры m , n и $τ$ так, чтобы результат смотрелся симпатичнее: \[ \begin{align} m &= R_1/R_2, \\ n &= C_1/C_2, \\ τ &= R_2C_2 \end{align} \]

Частота среза 2-полюсного фильтра примет форму \[ f_c=\frac{1}{2πτ\sqrt{mn}} \quad, \qquad \qquad \qquad [6.5] \] а добротность Q \[ Q=\frac{\sqrt{mn}}{1+m+mn(1-K)} \quad. \qquad [6.6] \]

Этих формул недостаточно для создания фильтров более высоких порядков стандартных типов ( Чебышева и т.п. ). Дополнительно требуются таблицы из работы Карки ( ##SLOA049B ) или программа расчёта фильтров. Но данные формулы показывают метод, которым можно разменивать один параметр на другой. Отметим, что единичный коэффициент усиления K=1 имеет то дополнительное преимущество, что активными элементами схемы могут служить микросхемы мощных буферов или повторители на отдельных транзисторах ²⁹.

Если возвратиться к прежним ограничениям для VCVS ( $R_1=R_2=R$ и $ C_1=C_2=C$ ) , формулы сократятся до \[ f_c=\frac{1}{2πRC}, \quad Q=\frac{1}{3-K}, \qquad [6.7] \] причём при K=3 конструкция становится неустойчивой ( Q$\to ∞$ ) . Отметим также, что при K=1 ( как на рис. 6.16 , где произошло знакомство с активными фильтрами ) схема становится совсем анемичной ( Q=0.5 ) .

6.3.2.E VCVS: итоги

VCVS минимизируют число элементов схемы ( по два полюса на ОУ ) и имеют дополнительные преимущества в виде дополнительного усиления без инверсии и лёгкой подстройки, низкого выходного импеданса, небольшого разброса номиналов компонентов и возможности выбора между большим усилением или высокой добротностью. Недостатки включают чувствительность к номиналам пассивных компонентов и параметрам ОУ и плохо подходят к задачам, требующим подстройки фильтра или высокой стабильности характеристик. Кроме того, рабочая полоса ОУ ( $ f_T $ или GBW ) должна быть много больше, чем $ f_c$ фильтра ³⁰. Некоторые из этих недостатков исправляют фильтры с управляемыми параметрами и биквадратные.

Упражнение 6.3
Разработайте VCVS фильтр Чебышева 6-го порядка с пульсациями 0.5 dB и частотой среза $ f_c$=100 Hz . Какое подавление будет у фильтра на частоте 1.5$ f_c?$

6.3.3 Фильтры с изменяемыми параметрами

Фильтр 2-го порядка, показанный на рис. 6.31 , гораздо сложнее, чем VCVS, но, несмотря на это, очень популярен из-за улучшенной стабильности и простоты подстройки. Его называют «фильтром с изменяемыми параметрами». Изначально он выпускался фирмой National в интегральном исполнении ( AF100 и AF150 ), но сейчас эти ИМС не производятся. Аналогичные микросхемы выпускает Burr-Brown/TI (UAF42 ) и Maxim ( MAX274, MAX275 ). Интегральный модуль включает все элементы схемы, кроме $R_G$ , $R_Q$ и двух $R_F$ . ИМС имеют отличные параметры и позволяют строить ФНЧ, ФВЧ и полосовые фильтры. В режиме полосового фильтра можно подстраивать частоту, не изменяя добротность или не изменяя ширину полосы. Как и VCVS фильтры с изменяемыми параметрами можно каскадировать для повышения их порядка. Частоту можно менять, если использовать для $R_F$ сдвоенный переменный резистор, но, возможно, при заданной характеристике настройки ( 1/$R$ ) будет удобнее применять последовательную схему ( рис. 6.34 ), при которой можно использовать и сдвоенный потенциометр, и умножающий ЦАП ( см. §6.3.3.C )

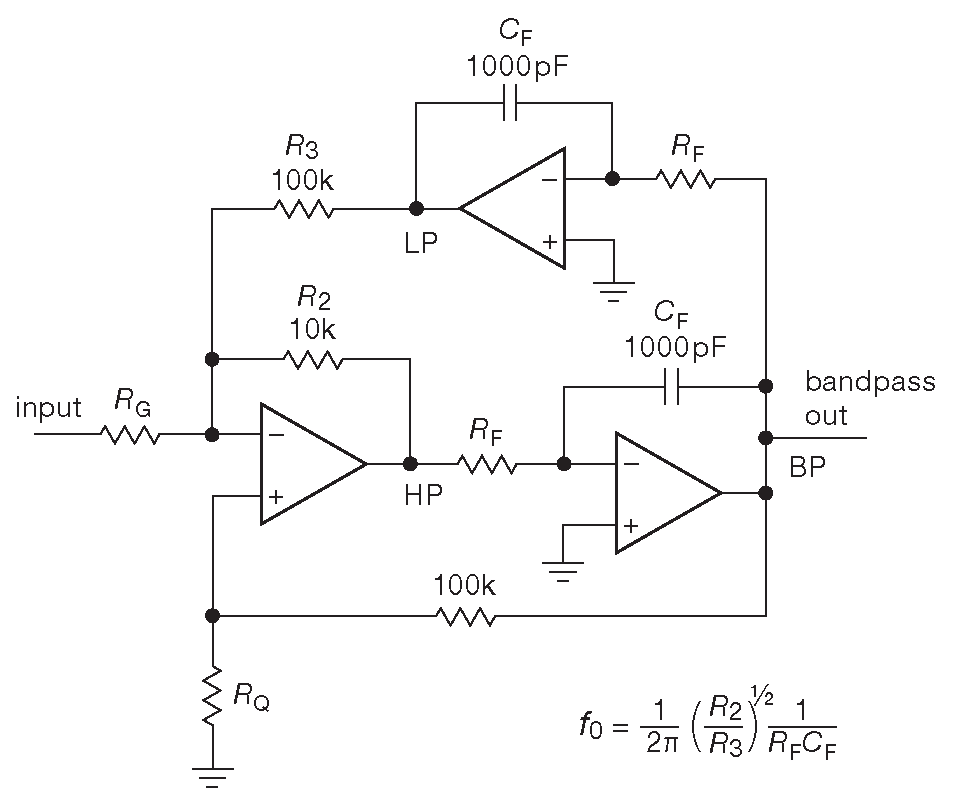
Рис. 6.31 Фильтр с управляемыми параметрами

Для указанных микросхем производители предлагают массу таблиц и формул, сообщают, как надо выбирать номиналы резисторов, чтобы получить фильтры Бесселя, Баттерворта или Чебышева любого порядка ( из некоторого набора ) и с любой характеристикой (ФНЧ, ФВЧ или полосовой ). Кроме полезных советов, производители включают в состав микросхем конденсаторы ³¹, поэтому всё, что требуется для работы - внешние резисторы.

==411

6.3.3.A Полосовой пропускающий фильтр

Фильтры с управляемыми параметрами с учётом их большого числа компонентов являются хорошим выбором для построения узкополосных ( высокодобротных ) полосовых фильтров. Такая архитектура имеет слабую чувствительность к компонентам, не предъявляет высоких требований к полосе ОУ и легко настраивается. Например, на схеме 6.31 изображён полосовой фильтр. Два резистора $R_F$ выставляют центральную частоту, а $R_Q$ и $R_G$ вместе определяют добротность и усиление на центральной частоте \[ \begin{align} R_E &= \frac{5.03 ×10^7}{f_0} \qquad &Ω, \qquad &[6.8]\\ R_Q &= \frac{10\space^5}{3.48Q + G — 1} \qquad &Ω, \qquad &[6.9]\\ R_G &= \frac{3.16Q ×10\space^4}{G} \qquad &Ω. \qquad &[6.10] \end{align} \]

Таким образом, можно сделать фильтр с фиксированной добротностью и переменной частотой, используя сдвоенный переменный резистор $R_F$ . Или можно менять резистором $R_Q$ добротность и, к сожалению, усиление, сохраняя неизменной частоту.

Упражнение 6.4
Рассчитайте величины резисторов для схемы 6.31 , чтобы получить полосовой фильтр с центральной частотой $ f_0$=1 kHz , добротностью Q=50 и усилением G=10 .

На рис. 6.32 показана удобная версия полосового фильтра. К сожалению, она требует четырёх ОУ, зато позволяет подстраивать ширину полосы ( т.е. добротность ) независимо от уровня усиления на центральной частоте. Оба параметра выставляются индивидуальными одиночными резисторами. Добротность, усиление и центральная частота становятся совершенно независимыми и рассчитываются по следующим уравнениям \[ \begin{align} f_0 &= \frac{1}{2πR_FC} , &[6.11] \\ Q &= \frac{R_1}{R_Q} , &[6.12] \\ G &= \frac{R_1}{R_G} , &[6.13] \\ R &≈ 10 kΩ . &[6.14] \end{align} \]

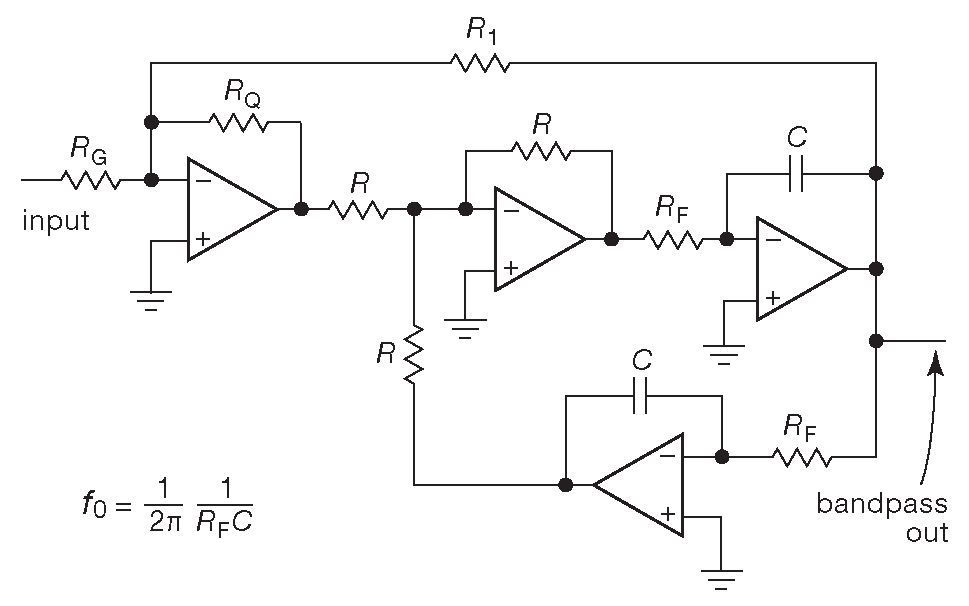
Рис. 6.32 Фильтр с независимой установкой усиления и добротности. Примечание. $R$ - два согласованных резистора

Биквадратный фильтр.

Очень похож на фильтр с управляемыми параметрами биквадратный фильтр ( рис. 6.33 ). Схема также состоит из трёх ОУ и может быть пересобрана из фильтра с управляемыми параметрами. У неё есть интересная особенность: частоту настройки можно менять ( резистором $R_F$ ) , не изменяя при этом ширину полосы ( вместо неизменной добротности ). Вот расчётные уравнения \[ \begin{align} f_0 &= \frac{1}{2πR_FC}, &[6.15] \\ BW &= \frac{1}{2πR_BC}, &[6.16] \\ G &= \frac{R_B}{R_G}. &[6.17] \\ \end{align} \]

Добротность получается из соотношения $Q=f_0/BW$ и равна отношению $R_B/R_F$ . Если центральная полоса изменяется, пропорционально изменяется и добротность, оставляя неизменным отношение $ f_0/Q$ .

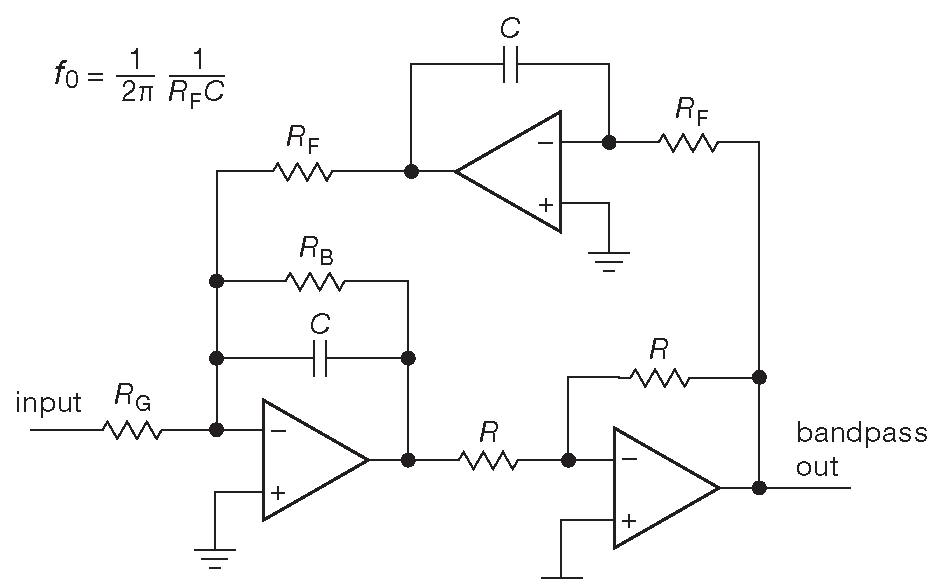
Рис. 6.33 Биквадратный фильтр

==412

При построении биквадратного фильтра с чистого листа ( вместо использования специализированных ИМС), алгоритм должен быть следующий.

[* Задать усиление на центральной частоте G и ] Выбрать ОУ, чья рабочая полоса $ f_T $ как минимум в 10...20 раз превышает произведение G×$ f_0$ .
Выбрать удобный номинал конденсатора неподалёку от значения $ C $=10/$ f_0$ μF , где $ f_0$ выражена в Hz .
Взять нужную центральную частоту и рассчитать $R_F$ по уравнению [6.15] .
Подставить нужную ширину полосы в уравнение [6.16] и вычислить $R_B$ .
По усилению на центральной частоте G и уравнению [6.17] рассчитать $R_G$.

Возможно, придётся скорректировать номиналы конденсаторов, если величины резисторов получаются слишком большими или слишком маленькими. Например, в высокодобротных фильтрах может потребоваться несколько увеличить $ C $ , чтобы удержать рост $R_B$ в разумных пределах ( или можно использовать «T-цепь», описанную в §4.5.5 ). Отметим, что $R_F$ , $R_B$ и $R_G$ видны со стороны ОУ как нагрузка, и нижнюю границу их номиналов не следует опускать ниже 5 kΩ . Не исключено, что при варьировании номиналов компонентов будет проще удовлетворить условию [1] , уменьшая усиление интегратора ( увеличивая $R_F$ ) и одновременно увеличивая усиление инвертирующего каскада ( увеличивая резистор обратной связи $R$ с исходным номиналом согласно уравнению [6.14] 10 kΩ ) .

Предположим, что надо собрать фильтр с характеристиками из упражнения 6.4 ( стр. 411 ). Начинаем с выбора примерного значения $ C $=0.01 μF . Затем рассчитываем $R_F$=15.9 kΩ ( $ f_0$=1 kHz ) и $R_B$=796 kΩ ( Q=50 , BW=20 Hz ). Наконец, $R_G$=79.6 kΩ ( G=10 ).

Упражнение 6.5
Разработать биквадратный полосовой фильтр с $ f_0$=60 Hz , BW=1 Hz и G=100 .

6.3.3.B Полосовые пропускающие фильтры высоких порядков

Как и в случае ФНЧ и ФВЧ, можно создавать полосовые фильтры более высоких порядков с почти плоской АЧХ в полосе пропускания и резким переходом к заграждению.

Делается это уже знакомым каскадированием полосовых фильтров низкого порядка в сочетании с должным выбором номиналов для получения характеристики нужного типа ( Баттерворта, Чебышева или что там ещё? ). Как обычно, «Баттерворт» плоский, «Чебышев» резкий, но неровный. Рассмотренные выше VCVS и биквадратные полосовые фильтры имеют 2-ой порядок ( два полюса ). Увеличение порядка за счёт дополнительных секций ведёт к «заострению» АЧХ и ухудшению переходных и фазовых параметров. «Рабочая полоса» такого фильтра определяется как ширина частотного диапазона, ограниченного точками «-3dB». Для фильтров с постоянными пульсациями полоса определяется по точкам, в которых АЧХ выходит из заданного коридора пульсаций.

Таблицы и алгоритмы проектирования сложных фильтров можно найти в справочниках по активным фильтрам или в сопроводительной документации на специализированные ИМС. Есть очень хорошие программы расчёта фильтров, в том числе свободные версии для PC.

6.3.3.C Электронное управление

Встречаются ситуации, когда требуется возможность подстройки ( или переключения ) параметров фильтра внешним сигналом, а не вращением ручки потенциометра. Примером может служить спектральный фильтр на входе АЦП, если частота выборки $ f_{samp} $ последнего должна меняться в некоторых пределах. В данной схеме частота среза фильтра $ f_c$ должна устанавливаться в соответствии с критерием Найквиста $ f_c≈ f_{samp}$/2 ( см. §6.2.3.C , §6.3.7.A и §13.5.1.B ). В активных фильтрах с архитектурой VCVS это можно делать в некоторых пределах с помощью аналоговых ключей, которыми можно коммутировать набор резисторов, определяющих характеристики. Но фильтры с управляемыми параметрами дают несколько более удобных способов как переключения, так и плавного изменения характеристик.

Цифровой потенциометр: Удобные микросхемы ( §3.4.3.E ), состоящие из длинной цепочки резисторов и набора МОП ключей с цифровым выбором нужного отвода ³² дают возможность изменения номинала задающего режим резистора, например, $R_F$ в схеме 6.31 , если добавить перед ним такой цифровой делитель ( и, возможно, буфер, если номинал окажется слишком мал), см. рис. 6.34 . Сдвоенный цифровой потенциометр ³³ позволит подстраивать одновременно пару $R_F$ , если потребуется подкрутить центральную частоту $ f_0$ в полосовом фильтре. Цифровые потенциометры могут иметь до 1024 ступеней, выпускаются как с линейной, так и с логарифмической характеристикой, и позволяют организовать достаточно удобное управление. Такие потенциометры не слишком точны по абсолютному значению ( обычно ±20% ), но гарантируют точное и стабильное отношение делителя ( 1% или лучше ), т.е. резисторы в цепочке хорошо согласованы. Поэтому в подобных схемах, где важны соотношения величин, цифровые потенциометры работают вполне успешно.

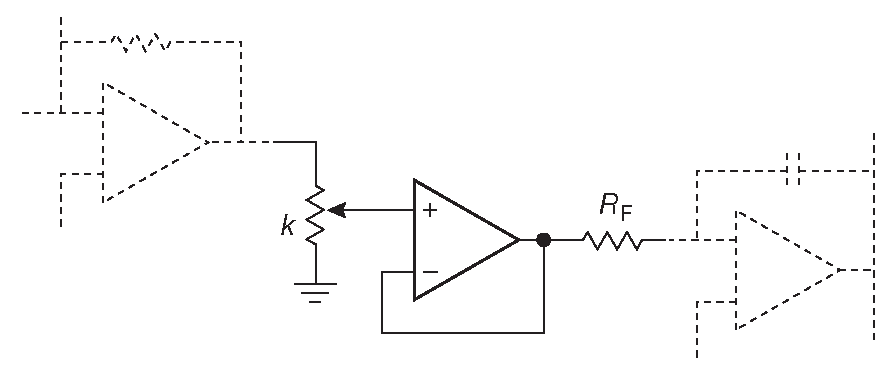
Рис. 6.34 Настройка частоты фильтра с управляемыми параметрами. Буфер на ОУ можно исключить, если строгая линейность по углу поворота потенциометра не нужна

==413

Умножающие ЦАПы: Ещё одним способом изменения $R_F$ в фильтрах с управляемыми параметрами является масштабирование выходных напряжений ОУ с помощью умножающего ЦАПа ( цифро-аналогового преобразователя ), вместо управляемого делителя. На выходе умножающего ЦАПа создаётся напряжение ( или ток ), пропорциональный произведению аналогового входного напряжения и цифрового кода. По сравнению с цифровыми потенциометрами ЦАП обеспечивает более высокое разрешение ( меньше шаг изменения ), он быстрее и часто имеет больший рабочий диапазон напряжений.
Аналоговые ключи: Если требуется только несколько режимов, можно использовать полупроводниковые аналоговые переключатели и набор отобранных резисторов. В таком варианте придётся учитывать наличие вполне конкретного сопротивления канала $R_{ON}$ .
Интегрированные переключатели: Есть несколько микросхем активных фильтров, в которых возможность изменения частоты среза предусмотрена изначально, и у кристалла есть выводы цифрового управления. Обеспечить непрерывное изменение параметра не получится, но можно сильно сэкономить на трудозатратах и компонентах. В качестве примеров можно назвать эллиптический ФНЧ 8-го порядка LTC1564, позволяющий выбрать частоту среза от 10 до 150 kHz с шагом 10 kHz , и MAX270 - 2-полюсный ФНЧ, который даёт 128 градаций частоты среза в диапазоне от 1 до 25 kHz .
Варианты с электронной настройкой: DSP и фильтры на переключаемом конденсаторе: Предыдущие способы предполагали использование электронного управления фильтрами непрерывного времени с помощью тех или иных заменителей переменных резисторов. Но, говоря об электронном управлении нельзя не упомянуть фильтры на переключаемом конденсаторе и цифровой обработке сигналов ( DSP ), в которых такое управление обеспечивается конструктивно. И те, и другие обсуждаются позднее в §6.3.6 и §6.3.7 .

6.3.3.D Активные фильтры с множественными обратными связями

В дополнение к VCVS ( Саллена-Ки ), биквадратным и фильтрам с управляемыми параметрами имеется ещё одна часто используемая архитектура. Её называют схемой «с множественными обратными связями» ( MFB ) или «с бесконечным усилением и множественными обратными связями» ( рис. 6.35 ). Здесь ОУ включён по схеме интегратора [* он отвечает за «бесконечное усиление», см. §4.2.6 ] , а не усилителя напряжения или повторителя. Рассчёт MFB фильтров так же несложен, как VCVS, и в сети полно отличных программ, помогающих в этом деле. Можно порекомендовать отличный сайт Уве Байса (Uwe Beis ) ( см. §6.3.8 ). MBF фильтры выпускаются в интегральном исполнении, например, LTC1563 - недорогая ( $2.30 ) микросхема аналогового фильтра с архитектурой MFB, удобная для создания спектральных фильтров и т.п. LTC1563-2 позволяет построить фильтр Баттерворта 4- или 5-го порядка, с частотой среза от 256 Hz до 360 kHz , а версия LTC1563-3 - фильтр Бесселя. Внутри стоят конденсаторы 27 pF и 54 pF , подстроенные с точностью 3% , что позволяет использовать внешние 1% резисторы из диапазона 7 kΩ...10 MΩ . Справочные данные производителя весьма информативны.

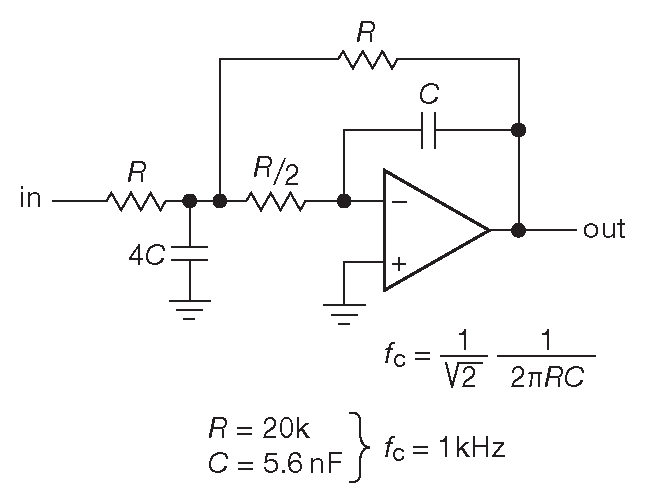
Рис. 6.35 Активный фильтр с множественными обратными связями. Здесь 2-полюсный ФНЧ

MFB имеет интересное преимущество перед VCVS: по мере приближения рабочей частоты фильтра к $ f_T $ используемого ОУ, рост выходного импеданса последнего меньше портит параметры схемы. Моделирование в SPICE работы VCVS и MFB фильтров низкой частоты Баттерворта 2-го порядка отлично выявляет данный эффект ( рис. 6.36 и 6.37 ). Была установлена частота среза 4 kHz , т.е. гораздо ниже $ f_T $ LF411 ( 4 MHz ). В VCVS варианте рост $Z_{out}$ усилителя позволяет входному сигналу пролезать на выход через первый конденсатор, а в MFB этот путь отсутствует ³⁴. Эффект не особо серьёзный и снижается по мере увеличения номиналов резисторов, как видно на рис. 6.36 . Этот недостаток не мешает VCVS жить, работать и оставаться по-прежнему популярным ³⁵.

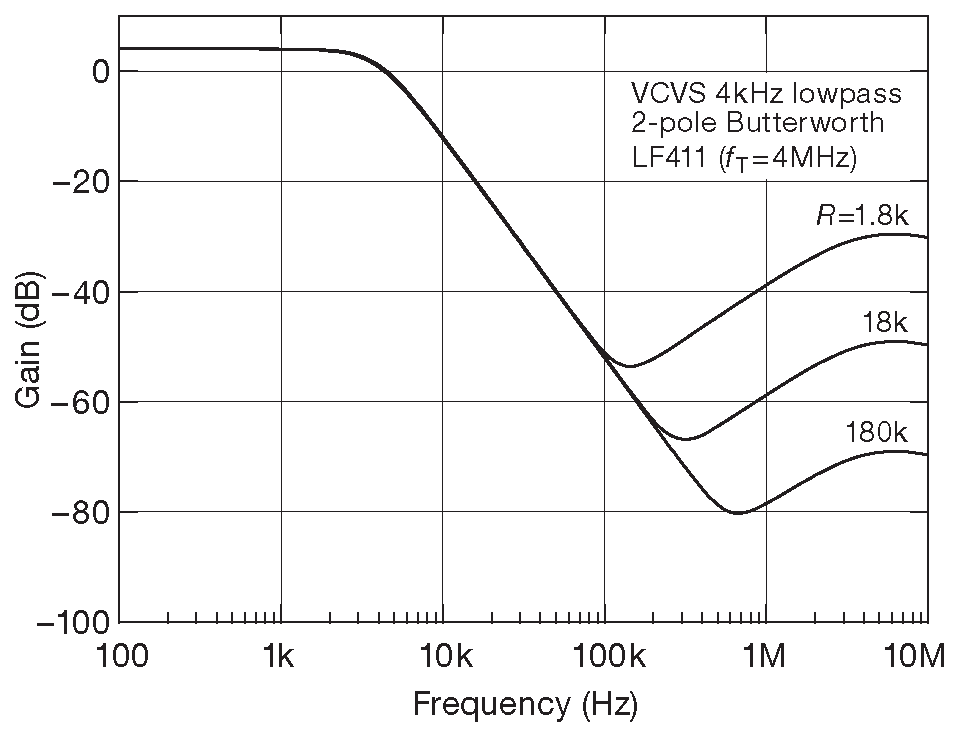
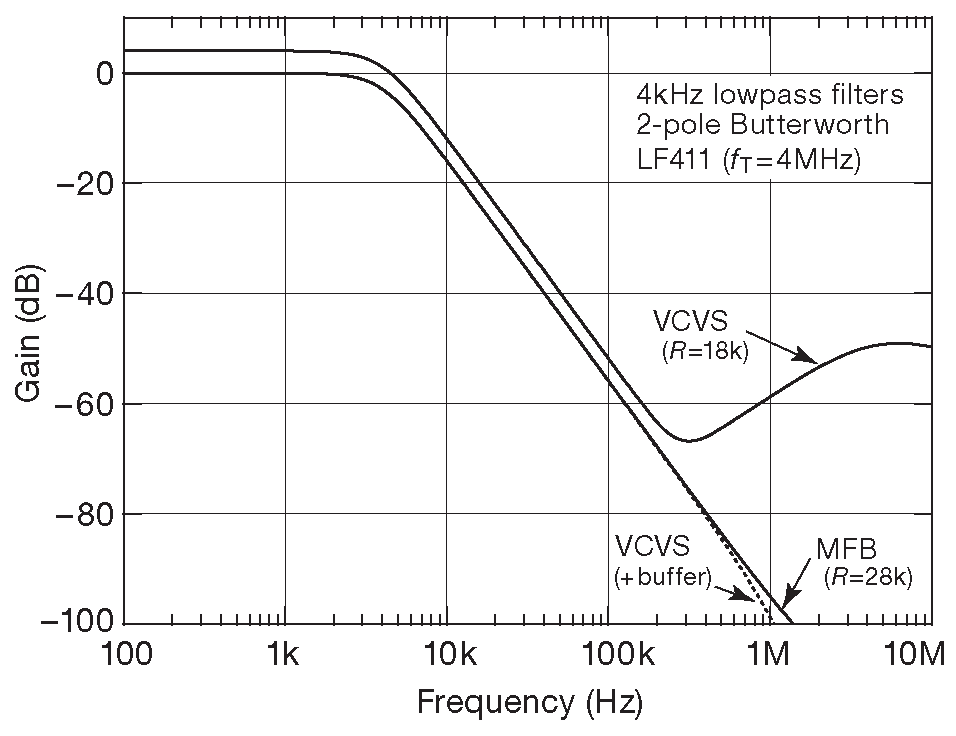
Рис. 6.36 Рост выходного импеданса ОУ ухудшает подавление VCVS фильтра ( Саллена-Ки ) на высокой частоте, позволяя входному сигналу пролезать на выход через входной резистор и конденсатор обратной связи ( $R_1$ и $ C_1 $ на рис. 6.28 ). Увеличение номинала резистора уменьшает этот эффект. См. также рис. 6.37
Рис. 6.37 Рост выходного сопротивления ОУ на высокой частоте мало влияет на подавление MFB фильтра в полосе заграждения ( см. рис. 4.53 ), если сравнивать с VCVS схемой. Недостатки последней можно снизить, добавив второй ОУ в качестве выходного каскада. Сигнал для него надо брать с неинвертирующего входа основного ОУ

==414

6.3.4 Фильтр-пробка «Двойное-T»

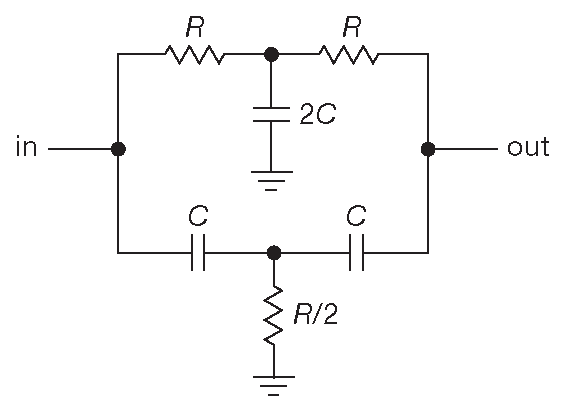
Рис. 6.38 Пассивный фильтр-пробка «двойное-T»

Пассивная RC цепь на рис. 6.38 имеет бесконечное подавление на частоте $ f_c=1/( 2πRC ) $ . Бесконечное подавление - явление для RC фильтров нехарактерное. В данном случае схема работает, складывая два сигнала, развёрнутые по фазе на 180° на частоте $ f_c$ . Такой способ предполагает хорошее согласование компонентов на частоте подавления. Схема называется «двойное-T» и используется для вырезания интерференционных составляющих, например, наводок от силовой сети. Проблема в том, что у неё такие же «мягкие» характеристики, как и у прочих RC цепей везде, кроме собственно $ f_c$ , где АЧХ падает, как в пропасть. Например, при работе от качественного источника сигнала «двойная-T» цепь показывает подавление 10 dB на удвоенной ( или на половине ) частоте заграждения и 3dB на учетверённой ( или одной четвёртой ). Одним из приёмов улучшения параметров заграждения является «активация» схемы наподобие фильтра Саллена-Ки ( рис. 6.39 ). Идея смотрится неплохо, но практика использования разочаровывает. По мере увеличения крутизны заграждающей характеристики, т.е. увеличения усиления в цепи вольтодобавки глубина нуля [* степень подавления на частоте заграждения] уменьшается.

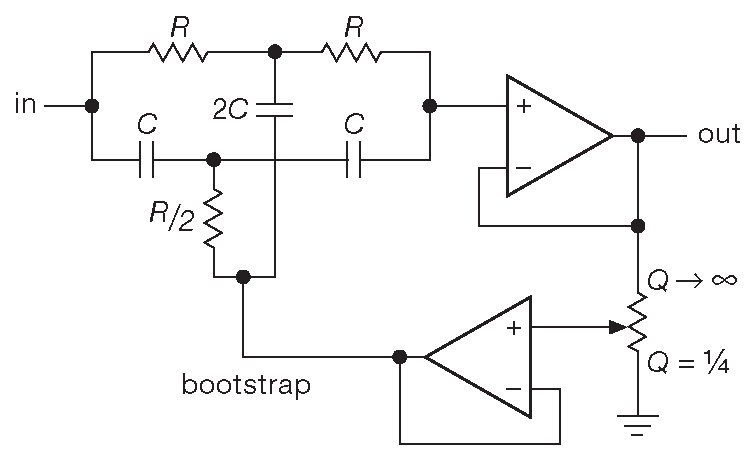
Рис. 6.39 «Двойное-T» с вольтодобавкой

Фильтры «двойное-T» доступны в виде готовых модулей на частоты от 1 Hz до 50 kHz при глубине подавления около 60 dB ( с некоторой деградацией при высоких и низких температурах ). Устройство легко повторить на дискретных компонентах, но, если нужно хорошее и стабильное подавление, придётся поискать резисторы и конденсаторы с хорошей стабильностью и низким температурным коэффициентом. Один из элементов должен быть подстраиваемым.

==415

Схемы «двойное-T» хорошо работают в качестве фильтров-пробок на фиксированную частоту, но попытка добавить в схему подстройку - это совершеннейший ужас, потому что для поддержания постоянства подавления три резистора должны подстраиваться одновременно. Зато есть очень простая RC цепь ( рис. 6.40A ), работающая подобно «двойному-T», но поддающаяся подстройке в широком диапазоне частот ( минимум две октавы ) одним потенциометром. Подобно «двойному-T» ( и большей части активных фильтров ) схема требует согласования компонентов. В данном случае требуется 3 идентичных конденсатора, а постоянный резистор должен быть точно в 6 раз больше, чем сопротивление потенциометра. Частота заграждения находится по формуле: \[ f_{notch}=\frac{1}{2πC\sqrt{3R_1R_2}}. \]

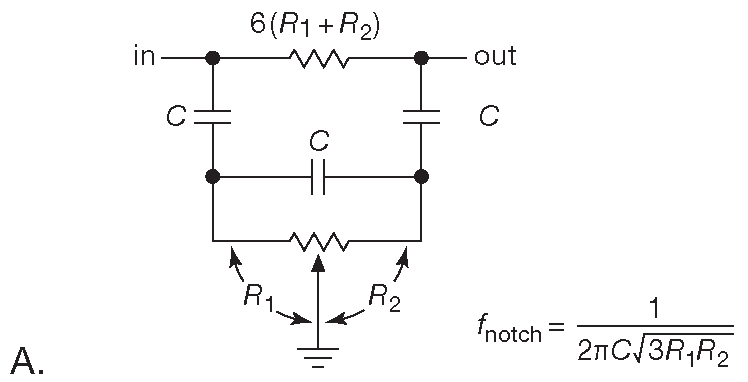
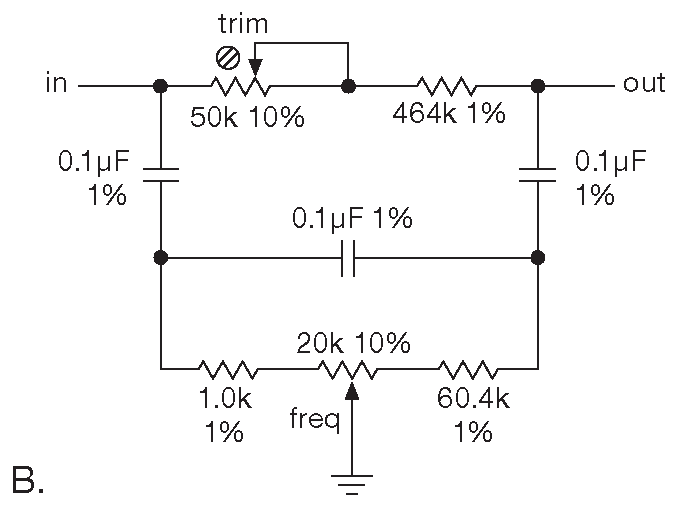
Рис. 6.40 Управляемый фильтр-пробка на мостовом дифференциаторе (A). Реализация для перестройки в диапазоне 25...100 Hz (B)

На рис. 6.40B показан вариант, допускающий перестройку в диапазоне 25...100 Hz . Триммером 50 kΩ подстраивается ( один раз ) глубина подавления на частоте заграждения.

Так же, как и в случае пассивной цепи «двойное-T», данный фильтр ( известный как мостовой дифференциатор ) имеет плавный спуск кривой подавления вне частоты заграждения и бесконечное подавление ( предполагается хорошее согласование величин компонентов ) на частоте заграждения. Его тоже можно «активировать», добавив в движок переменного резистора вольтодобавку, как на рис. 6.39 , с коэффициентом усиления чуть менее единицы. Приближение усиления к единице делает пик на графике подавления Уже, но одновременно вызывает появление на АЧХ неприятного выброса выше частоты заграждения и уменьшает общую величину подавления.

==415

²⁴ Или даже на отдельных транзисторах, как в фильтрах Саллена-Ки. <-

²⁵ Итоговые конфигурации часто идентичны таковым у схем непрерывного времени, например, «фильтрам с изменяемыми параметрами» или «биквадратным» . <-

²⁶ The Art of Electronics, 2nd edition, стр. 249 и 549. <-

²⁷ «Анализ архитектуры Саллена-Ки» ##SLOA024B ( 2002 ) и «Разработка активного фильтра нижних частот» ##SLOA049B ( 2002 ). <-

²⁸ Предупреждение: обозначения элементов $R$ и $ C $ в книге соответствуют таковым из оригинальной публикации Саллена и Ки, но во многих других местах, включая статьи Карки, $ C_1 $ и $ C_2$ поменяны местами. <-

²⁹ Уравнения можно преобразовать, чтобы выразить m через n при заданной величине Q . Для этого надо задать переменную $\alpha=(n/( 2Q^2 ))-1$ , тогда $m=\alpha+\sqrt{\alpha^2-1}$ . <-

³⁰ По утверждению многих авторитетных источников речь идёт о соотношении $ f_T $ ≥ 50×$Q^2$×$f_c$ , где Q одной секции на ОУ задаётся в терминах усиления K ( также как в таблице ), т.е. Q = 1/(3-K) . Иногда встречается альтернативные условия требуемой полосы $ f_T $ ≥ 50×$ f_c$ или $ f_T $ ≥ 50×K×$ f_c$ , но всё это цифры одного порядка. [* Интересно, что для генераторов Вина на RC паре для устойчивой генерации без ограничения амплитуды требуется усиление G=3 §7.1.5.B ] . <-

³¹ И, конечно, эти, и все прочие реализации активных фильтров, не требуют катушек индуктивности. <-

³² Как управлять такими штуками рассказывается в Части 10 [* §10.3.3.C ] . <-

³³ В одном корпусе может быть и один, и два, и четыре, и даже шесть потенциометров. <-

³⁴ Эффект описывается в публикациях Джеймса Кирки ##SLOA024B и ##SLOA049A, а также в статье Дейва ван Эсса ( Dave Van Ess ) «О чём не говорят в статьях о фильтрах Саллена-Ки» (“What Sallen-Key Filter Articles Don’t Tell You”) в EN-Genius analogZONE. <-

³⁵ Простой способ справиться с проблемой на высокой частоте - дополнительная RC секция на выходе. Скажем, 200 Ω+7.5 nF сформируют дополнительный срез на частоте 100 kHz . <-