13.5 Аналогово-цифровые преобразователи

==900

СтОит возвратиться чуть назад в главу §13.1 «Предварительные сведения», чтобы вспомнить некоторые параметры выбора конвертора ( одинаковые и для ЦАПов, и для АЦП ). Сейчас нужно не углубляться в подробности самого процесса преобразования, а сконцентрироваться на общих вопросах, в числе которых

параметры ( скорость, точность и т.п. ),
цифровой интерфейс ( параллельный или последовательный, однополярный или дифференциальный и т.д. ) и
степень интеграции ( один или несколько инверторов в корпусе, отдельный или встроенный в микроконтроллер или систему на кристалле ).

В большинстве случаев дело приходится иметь с фабричной продукцией, а не строить что-то своё домотканое. Но важно понимать, как работают различные методы аналогово-цифровых преобразований, чтобы случайно на попасть в какую-нибудь хитрую ловушку, свойственную какому-то конкретному варианту.

13.5.1 Оцифровка: наложения, частота выборки и глубина выборки

Оставим разные ненадолго скучные подробности АЦП и разберёмся с выборками , которые будут постоянно встречаться, когда дело дойдёт до знакомства с методами аналогово-цифровых преобразований.

При конвертации аналогового сигнала ( например, звуковой волны ) в последовательность цифровых величин ( т.е. цифр, соответствующих мгновенному значению напряжения в последовательные моменты времени ) нужно уметь выбирать как точность измерения напряжения ( глубину выборки ), так и частоту , с которой делаются выборки. Эта тема встречается в Части _6 ( §6.3.7A ) при рассмотрении ФНЧ, предотвращающих наложение спектров . Теперь рассмотрим этот вопрос подробнее в контексте оцифровки формы аналогового сигнала.

13.5.1.A Глубина выборки

Рассмотрим сначала глубину выборки и эффекты, с ней связанные ( потому что их проще понять ): разбиение по 2ⁿ одинаковым уровням ( n разрядам ) ограничивает динамический диапазон величиной (6×n) dB . Форма сигнала, прошедшего такую операцию с учётом того, что он занимал полный диапазон преобразования, будет искажена, т.е. сигнал получит шумы квантования [* в ходе округления до ближайшего уровня квантования ] на уровне 2^–n ( т.е. 100/(2ⁿ) процентов ).

Например, 16-разрядное квантование звука ( стандарт, используемый в звуковых CD ) ограничивает динамический диапазон величиной 96 dB и минимальным уровнем искажений 0.0015% . Если учесть, что реальный сигнал одновременно и ограничивается по динамическому диапазону, и получает увеличенные искажения, становится понятно, что хорошо спроектированная система должна иметь достаточную глубину квантования ( и частоту выборки ), чтобы не слишком ухудшать качество сигнала.

На следующем уровне подробностей есть кое-что ещё помимо числа разрядов: нелинейность ( немонотонность ), шум, помехи и т.д., и все они вносят «посильный вклад» в качество оцифрованного сигнала. Наиболее полный показатель, учитывающий бОльшую часть указанных проблем, зовут «ENOB» - эффективное число битов. Она встретится чуть позднее ( см., например, рис. 13.56 ).

13.5.1.B Частота опроса и фильтрация

Этот вопрос несколько сложнее ( и интереснее ). В противоположность интуитивным ожиданиям, сигнал, оцифрованный с частотой, более чем вдвое превышающей самую высокочастотную компоненту измеряемого спектра не имеет потерь информации. Ничего не теряется и в промежутках между точками измерения. Это наблюдение именуется «теоремой Найквиста» ( и имеет свою группу противников, голосящих о душе музыки, которую убивают цифры ) ²⁸.

==901

Читатель, не склонный к преклонению перед авторитетами может поинтересоваться, что случится, если нарушить правило через субдискретизацию ( т.е. с частотой, которая ниже требуемой согласно теореме ). За ответом обратимся к рис. 13.23 , где синусоидальное напряжение с частотой 100 Hz , требующее \( f_{samp} \) > 200 sps , оцифровывается на скорости 90 sps , т.е. гораздо ниже предела Найквиста. В результате отсчёты сложатся в фантомный сигнал с частотой 10 Hz [*] . Именно он зовётся ложной низкочастотной копией сигнала ( фантомная копия ), и это совсем не то, что обычно хотят получить в ходе изменений ²⁹. Проще говоря, для заданной частоты опроса \( f_{samp}\space\) аналоговый сигнал должен проходить через специальный спектральный фильтр, чтобы в спектре сигнала не осталось никаких существенных исходных составляющих с частотой, большей \( f_{samp} \) /2 . Или иначе, для аналогового сигнала, занимающего полосу вплоть до частоты \( f_{max} \) , минимальная частота опроса должна составлять 2\( f_{max} \) . Можно проводить выборку чаще, чем предписывает теорема Найквиста \( f_{samp} \) > 2\( f_{max} \) , и это на самом деле достаточно разумно, потому что позволяет упростить условия фильтрации, как будет видно позднее.

[*]
[* Т.е. мы получили разностный сигнал \( f_{100 Hz}-f_{samp}=f_{alias}\space\) или выполнили сдвиг вниз по частоте. А основной сигнал теперь можно отфильтровать и работать только с низкочастотной «копией». Хм. А если в качестве \( f_{samp}\space\) использовать т.н. «промежуточную частоту», то можно получить «синхронное детектирование». А вы говорите, «вредно» ##Zk ].

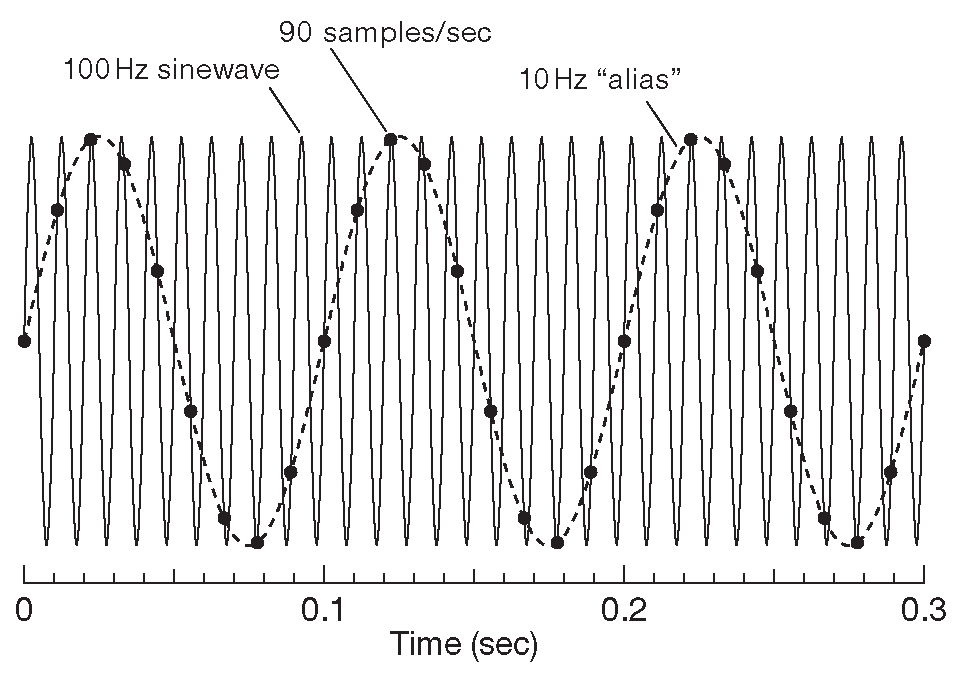
Рис. 13.23 Дискретизация с частотой ниже предела Найквиста создаёт фантомные копии . Синусоидальный сигнал 100 Hz ( непрерывная линия ), опрашиваемый с частотой 90 Hz ( т.е. гораздо ниже, чем нужные 200 sps ), создаёт фантомный сигнала 10 Hz ( точки, соединённые пунктирной линией )

Очень полезно глянуть на последствия фильтрации в частотной области. На рис. 13.24A широкополосный сигнал пропускается через неэффективный 2-секционный RC фильтр, в котором частота «-3dB» каждой секции равна пределу Найквиста ( \( f_{samp} \) /2 ). Частотные компоненты в запрещённой зоне ошибочно оцифровываются, как показано на рисунке ³⁰, засоряя интересующую полосу сигнала. Убрать паразитные составляющие позднее нельзя: для цифрового сигнала эти компоненты уже внутриполосные.

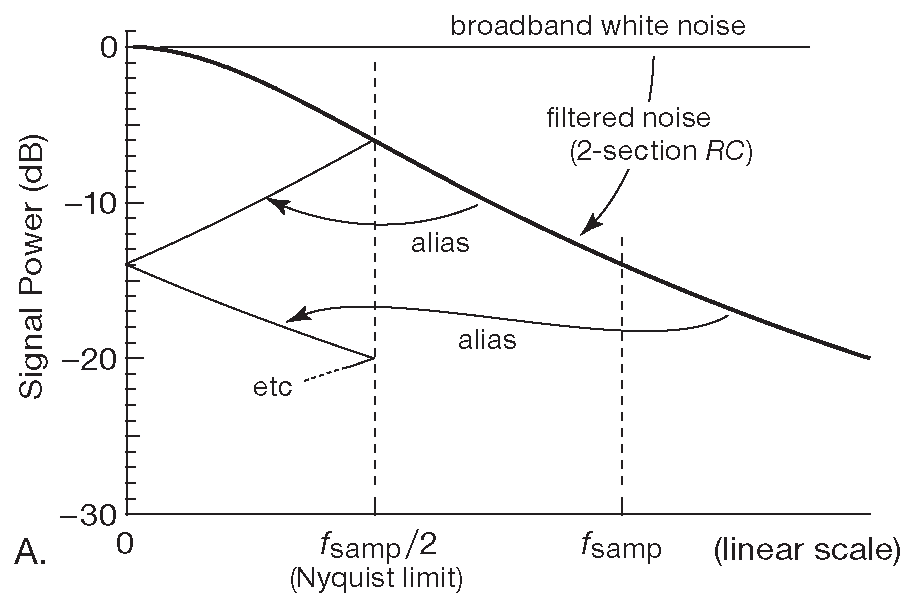
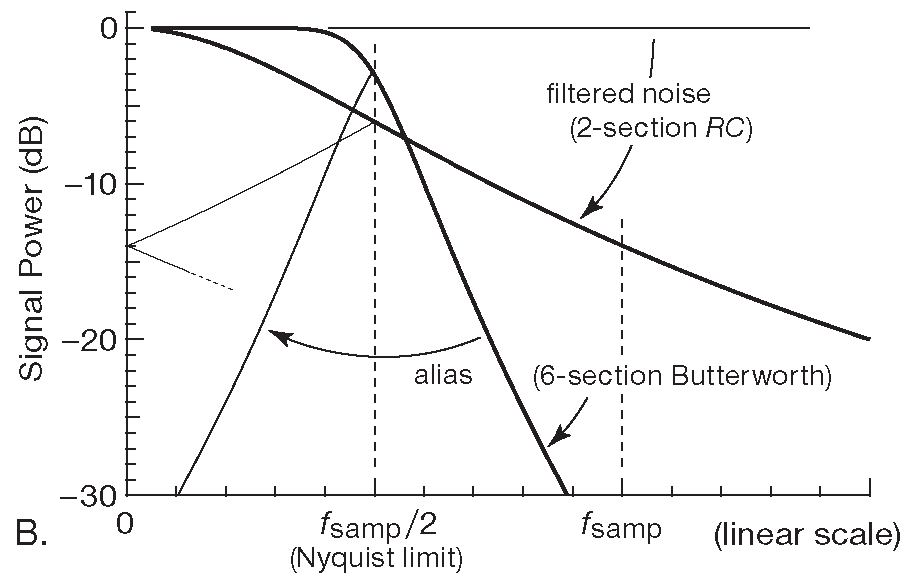
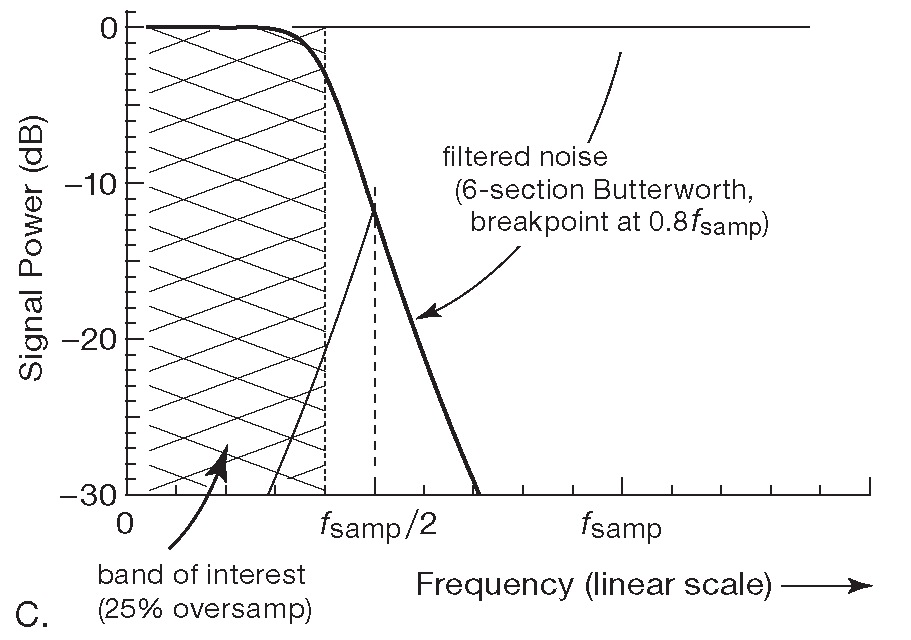
Рис. 13.24 Опрос с недостаточной и с избыточной частотой и появление фантомного сигнала. (A) Опрос сигнала, некоторые частотные компоненты которого лежат выше предела Найквиста ( \( f_{samp} \) /2 ), ведёт к появлению в цифровом сигнале фантомных составляющих, перемешанных с реальным сигналом. 2-секционный RC фильтр оказывается слишком пологим и пропускает достаточно энергии внеполосного сигнала, чтобы замусорить интересующий спектр. (B) Более резкий фильтр эффективнее, но результат всё равно включает внеполосные компоненты. (C) Опрос с частотой, повышенной относительно предела Найквиста ( здесь на 25% \) ) , позволяет получить защитный зазор, который учитывает характеристики входного фильтра и сильно снижает мощность внеполосного сигнала

==902

Фильтр, защищающий от наложения спектров , с резкими срезами работает лучше, что видно на рис. 13.24B , где показан фильтр Баттерворта 6-го порядка с частотой «-3dB», равной \( f_{samp} \) /2 . Но ситуация по-прежнему далека от идеала, и в сигнал попадает много посторонних гармоник. Особенно страдает высокочастотная область.

Остаётся только поднимать частоту опроса выше предела Найквиста, как на рис. 13.24C , где частота опроса повышена на 25% относительно минимально необходимой для интересующей полосы. Это позволяет получить защитный зазор на переходе от полосы пропускания к полосе заграждения. Отметим, что частота «-3dB» фильтра равна верхней границе рабочей полосы, т.е. лежит ниже частоты опроса.

Именно так надо поступать, если интересует качество сигнала. Возвращаясь к аудио-CD с полосой 20 kHz , фильтр с вертикальными границами и частотой среза 20 kHz позволил бы проводить измерение с частотой Найквиста \( f_{samp} \) =40 kHz , но стандарт указывает величину 44.1 ksps ( на 10% выше ), что даёт защитный зазор шириной 20% ³¹. Чуть дальше вопрос наложения спектров будет рассматриваться в частотной области ( рис. 13.60 ) в приложении к достоинствам сигма-дельта преобразования.

Отметим свойственные спектральным фильтрам недостатки. Многозвенные аналоговые фильтры с резким переходом к заграждению, например, фильтр Чебышева, имеют плохие параметры во временной области: выбросы, звон, посредственные фазовые характеристики, чувствительность к номиналам компонентов и т.д. ( см. рис. 6.25 и 6.26 ). Типы и характеристики фильтров подробно разбираются в Части _6 ( а именно в §6.2.5 ), а деструктивная роль шума в Части _8 .

13.5.2 Техника аналогово-цифрового преобразования

Существует шесть методов преобразования аналоговых величин в цифровые, каждая со своими плюсами и минусами. В следующих параграфах они будут разобраны последовательно и с примерами, а здесь приводится только краткий общий обзор.

«Флэш» или параллельные: §13.6 . Входное напряжение сравнивается с набором образцовых уровней. Обычно это делается с помощью 2ⁿ компараторов, в результате получается n-разрядный результат. Есть варианты схемы, включающие конвейерные или многодиапазонные , в которых преобразование ведётся в несколько этапов, каждый из которых обрабатывает «остаток» от предыдущих менее точных шагов.
Последовательное приближение: §13.7 . Внутренняя схема создаёт последовательные промежуточные коды, которые преобразуются внутренним ЦАПом в напряжение и сравниваются с входным сигналом. Для n-разрядного преобразования требуется n таких шагов. Внутренний ЦАП может быть выполнен в виде R-2R делителя или в виде набора конденсаторов с двоично взвешенными номиналами. Второй вариант используется в методе известном как ЦАП с распределением заряда .
Преобразование напряжения в частоту: §13.8.1 . На выходе формируется последовательность импульсов ( или сигналов иной формы ), частота которых пропорциональна входному напряжению. В асинхронных схемах генератор внутренний и работает постоянно. Синхронные преобразователи V/F требуют внешнего тактирования и пропускают часть тактовых импульсов на выход так, чтобы средняя выходная частота была пропорциональна входному напряжению.
Однократное интегрирование: §13.8.2 . Время, необходимое внутреннему линейно возрастающему напряжению ( конденсатор, заряжающийся от источника тока ), чтобы вырасти от нуля до потенциала на входе, пропорционально входному напряжению. То же время преобразования используется в качестве строба, пропускающего тактовые импульсы на счётчик. Отметим, что широтно-импульсная схема использует такой же подход ( пилообразное напряжение ), чтобы получить время активной части каждого рабочего цикла.
Двойное и многостадийное интегрирование: §13.8.3 , §13.8.4 , §13.8.6 . Это развитие схемы однократного преобразования, которое компенсирует ошибки от сдвига компаратора и нестабильности компонентов. При двойном интегрировании конденсатор сначала фиксированное время заряжается током, пропорциональным входному напряжению, а затем разряжается до нуля фиксированным током. Время разряда пропорционально входному напряжению. В варианте «четырёхстадийного» ( двойного преобразования с автокоррекцией нуля ) используется два последовательных «двойных преобразования». Первое для измерения входного напряжения, а второе - для измерения нулевого потенциала. Техника многостадийного преобразования чуть отличается. Элементарный цикл преобразования состоит из последовательной серии двойных измерительных циклов ( измерение входа - вычитание тока ) с двумя циклами коррекции: одним в начале процесса измерения и одним в его конце. Некоторыми своими характеристиками он очень походит на сигма-дельта преобразование.

==903

Сигма-дельта: §13.9 . Состоит из двух частей: модулятор преобразует входное напряжение в последовательный двоичный поток импульсов , а затем цифровой фильтр нижних частот прореживает поток, получая выходной n-разрядный код. Проще всего ( помогает, впрочем, не очень ) представить модулятор в виде интегратора, который превращает разницу между входным напряжением и величиной, закодированной цифровым потоком, в значение следующего бита [* интегратор, потому что он всё время пытается сгладить указанную разницу ] . Варианты метода включают использование последовательности взвешенных интеграторов или потока слов шириной несколько бит или их комбинацию. Сигма-дельта АЦП являются одновременно и популярными и непонятными, поэтому в этой части им отведена целая глава.

==903

²⁸ Данный факт может быть доказан математически. За исключением некоторого набора специальных последовательностей исходный сигнал отлично восстанавливается: \(v( t )=Σ v_i sinc[π( f_st — i )]\) , где \( f_s\) - частота выборок, а \(v_i\) - амплитуда i-той выборки. ) <-

²⁹ См. важное исключение в §13.6.3 . <-

³⁰ Такие картинки получаются простым отражением контура АЧХ от предела Найквиста [* и частоты 0 Hz ] . <-

³¹ Гораздо более высокая степень избыточности частоты дискретизации , многократно превосходящая предел Найквиста, будет рассматриваться в теме сигма-дельта преобразования. <-