13.9 (II) АЦП IV: Сигма-дельта

==928

13.9.7 Моделирование

Предположим, есть желание увидеть, как сигналы проходят через сигма-дельта АЦП. А именно, хочется получить поток битов из случайного аналогового сигнала и итоговые числа ( изображаемые в виде точек на одном графике с входным сигналом ), причём делать это в частотной области, где перераспределение должно быть хорошо заметно.

Подобную задачу можно решить в пакете Mathematica® ⁸³, используя следующие шаги.

Создаётся псевдослучайный сигнал с плоским спектром и гауссовым распределением амплитуд и выводится для 8192 последовательных промежутков времени.
Отфильтровывается идеальным ФНЧ со срезом на уровне 1/8 от исходной частоты и нормализуется, чтобы амплитуда попала в диапазон ±1 . Это будет «аналоговый входной сигнал». Максимальная частота полученного сигнала обозначается как частота Найквиста $ f_{nyq}$ .

==929

«Входной сигнал» превращается в поток битов со значениями ±1 с помощью моделирования передискретизирующего сигма-дельта модулятора первого порядка ( в котором интегратор выполнен в виде отдельного цифрового аккумулятора ). В примере взят коэффициент передискретизации 8× : частота тактирования будет равна $ f_{clk} $ = 8 × 2$ f_{nyq}$ ( $ f_{clk}\space$ должна быть кратна 2$ f_{nyq}$ ).
Полученный битовый поток рассматривается как аналоговый сигнал и пропускается через ФНЧ с такой же характеристикой, как и фильтр на шаге (b), чтобы получить выходные отсчёты. Выходные отсчёты появляются с частотой 8× и требуют прореживания ( например, использованием только каждого восьмого бита ), чтобы превратиться в выходной сигнал АЦП с частотой 1× ( т.е. в два раза большей, чем $ f_{nyq}$ - максимальной частоты во входном сигнале ).

На рис. 13.57 показан характерный кусок более длинного результата моделирования, иллюстрирующий картину во временной области. Отметки на горизонтальной оси соответствуют частоте 1× ( пределу Найквиста ), а отдельные точки следуют с частотой 8× . Входной сигнал - извилистая непрерывная линия, проходящая почти по точкам [* точки - представление выходных чисел, в которых уже есть ошибка квантования, в аналоговом виде ] . Поток битов показан там же в виде точек на уровнях ±1 . Наконец, ошибка ( цифровой выход минус аналоговый вход в каждой точке тактовой частоты 8× ) - линия точек малой амплитуды. По этим графикам можно на глаз прикинуть точность преобразования. Здесь она составляет 6% от полной амплитуды и превращается в динамический диапазон SNR 16:1 или 24 dB , т.е. хорошо соответствует графику на рис. 13.56 .

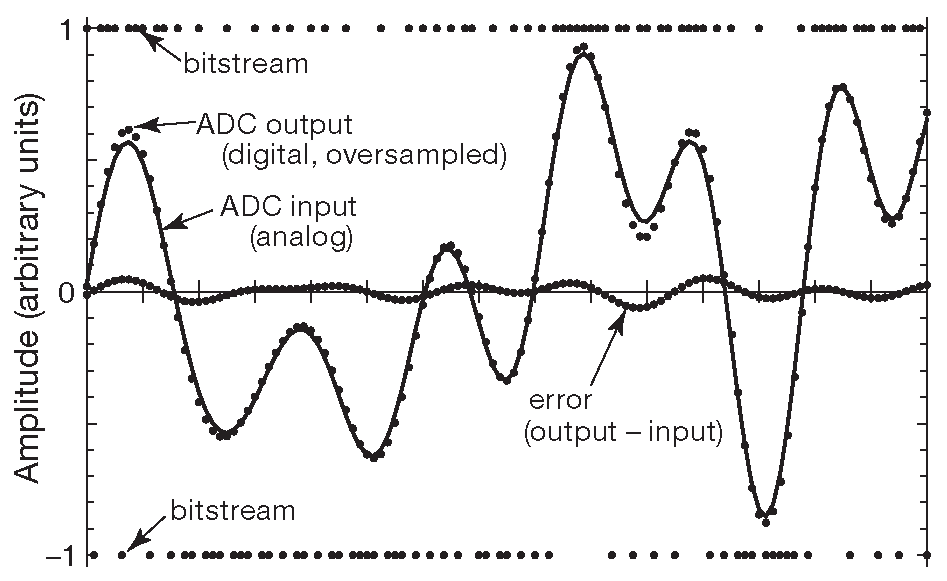
Рис. 13.57 Моделирование сигма-дельта АЦП первого порядка с восьмикратной передискретизацией

==930

Из того же моделирования можно вывести частотный спектр входного сигнала и цифрового результата и разницу между ними ( сигнал ошибки ), см. рис. 13.58 . Спектр ⁸⁴ простирается до половины частоты передискретизации, т.е. до границы в 4 × 2$ f_{nyq}$ [* до 4× ] . Верхний график показывает плоский входной спектр, чётко срезанный идеальным фильтром на частоте $ f_{nyq}$ . Средний график - спектр битового потока, в этом случае он рассматривается как аналоговое напряжение, которое предположительно содержит копию входного сигнала и какое-то количество шума квантования. Спектр простирается до частоты передискретизации [* на рисунке обрезан на уровне «4×» ] . По рисунку видно, что картина соответствует ожиданиям: почти точное повторение спектра до частоты $ f_{nyq}$ и дополнительный шум квантования, увеличивающийся пропорционально частоте. Чтобы оценить разницу, надо вычистить разность выходного и входного спектров - нижний график. Виден почти линейный рост от постоянного тока и до границы графика. Весь шум выше частоты $ f_{nyq}$ будет вырезан выходным цифровым фильтром АЦП ( рис. 13.50 ), через который проходит весь битовый поток [* при этом фильтр работает с потоком как с набором цифровых значений ] .

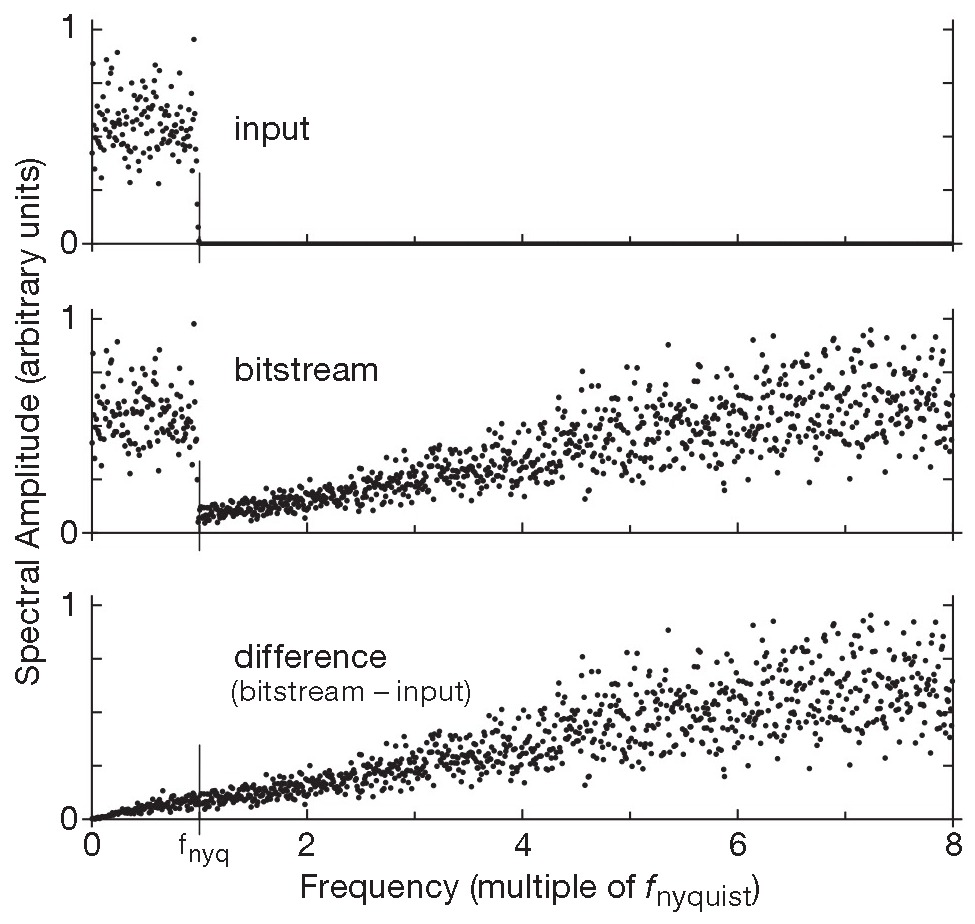
Рис. 13.58 Частотный спектр сигма-дельта АЦП первого порядка по результатам моделирования

Линейный характер спектра шума квантования в модуляторе первого порядка меняется на квадратичный в модуляторе второго порядка, и т.д. по мере роста порядка. Изменение характера графика соответствует улучшению точности ( или SNR , или эффективному числу разрядов ) согласно рис. 13.56 .

13.9.8 Что там у ЦАПов?

Как указывалось ранее, та же схема низкочастотной фильтрации битового потока, но порождаемого уже с помощью цифрового модулятора ( рис. 13.59 ), используется в сигма-дельта цифро-аналоговых преобразователях. В качестве входного сигнала такой модулятор принимает n-разрядные слова. Если сравнить его с аналоговым коллегой в АЦП ( рис. 13.51 ), то можно обнаружить, что разностный усилитель превратился в цифровое вычитающее устройство, а интегратор - в цифровой же аккумулятор. На каждом такте его текущее содержимое складывается с новым входным словом и вновь защёлкивается до следующего такта. Аналоговый компаратор заменён на цифровой вариант, который в наиболее простом случае передаёт далее по схеме знаковый разряд ( или MSB в случае беззнакового кода со смещением ). В этой точке образуется поток 1-разрядных слов, которые сообщают, больше или меньше середины шкалы было содержимое аккумуляторе. Наконец, 1-разрядный ЦАП заменило «n-разрядное АЦП», которое просто подаёт на сумматор максимальное или минимальное n-разрядное число, соответствующее выходному 1-разрядному значению в нужной кодировке. Для n-разрядного беззнакового кода со смещением это будут числа из n нулей или n единиц, т.е. для 16 разрядов - 0x0000 или 0xFFFF ) ⁸⁵.

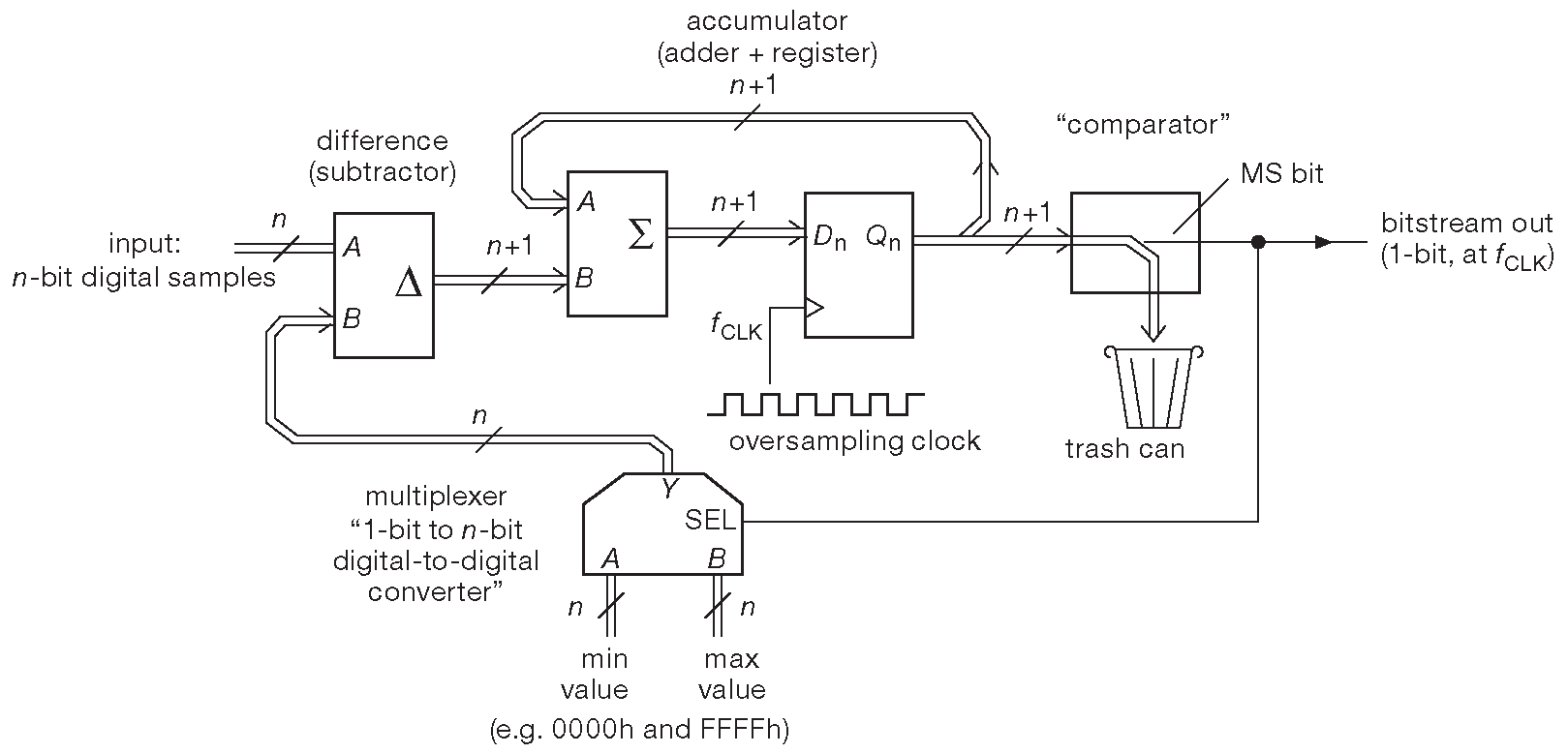
Рис. 13.59 Цифровой модулятор первого порядка из сигма-дельта ЦАПа. Внутренняя разрядность схемы увеличена, чтобы избежать переполнения при сложении

Так же, как и в случае аналогового модулятора в АЦП, цифровой модулятор в ЦАПе может иметь порядок отличный от единицы. Для этого надо каскадировать связку «вычитатель-аккумулятор» ( т.е. цифровой ФНЧ ). Так же, как и в аналоговой схеме, модулятор не ограничивается 1-битными выходными числами. Он может, и эта опция используется достаточно часто, выдавать поток многоразрядных слов. В таком варианте несколько старших битов направляются как в выходной поток, так и в цепь цифровой обратной связи. Для 2-разрядного модулятора ( четыре уровня ) 2-разрядные выходные слова будут

преобразованы в 4-уровневый аналоговый сигнал ( например, с помощью резистивного делителя ), а тот, в свою очередь, пропущен через аналоговый ФНЧ, чтобы получить в итоге аналоговое выходное напряжение; и
одновременно превращёны в одно из четырёх n-разрядных значений перекрывающих весь диапазон чисел ( для 16 разрядов это могут быть 0x0000 , 0x5555 , 0xAAAA и 0xFFFF ) и поданы обратно на входной вычитатель.

На выходе сигма-дельта ЦАПа как и на выходе сигма-дельта АЦП, стоит фильтр нижних частот. Но у ЦАПа это аналоговый фильтр, который лишён богатых возможностей цифрового варианта. Результатом является ухудшение характеристик: увеличение прохождения тактовой частоты на выход и чувствительность к джиттеру - дрожанию фазы тактового сигнала. Это обычная проблема «непрерывных» во времени линейных схем ⁸⁶.

==931

13.9.9 Плюсы и минусы ΣΔ конверторов

13.9.9.A Достоинства

Линейность, монотонность, точность: 1-Разрядные сигма-дельта конверторы гарантируют монотонность, они изначально линейны и спокойно достигают точности 24 разряда на звуковых частотах.
Дешевизна: Сигма-дельта АЦП используют недорогую и точную цифровую фильтрацию, а благодаря передискретизации, нуждаются в простом аналоговом спектральном фильтре на входе ( рис. 13.60 ).

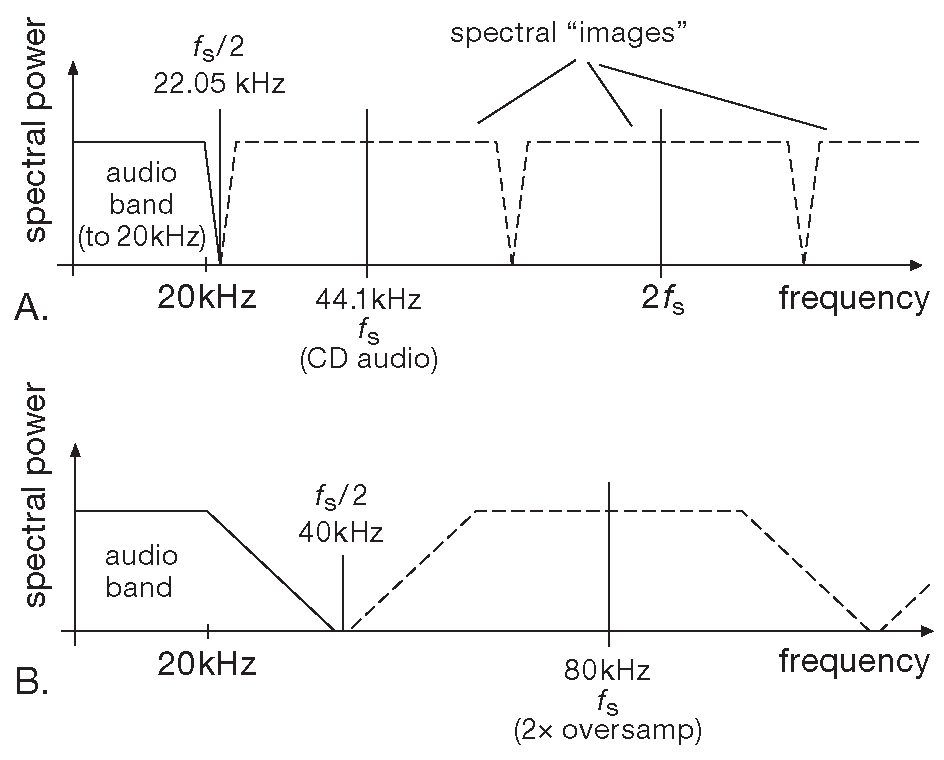
Рис. 13.60 Спектр аналогового сигнала, который измеряется на периодической основе с тактовой частотой $ f_s$ , включает зеркальные копии, расположенные симметрично относительно $ f_s$ и её гармоник. Аналоговый сигнал перед оцифровкой должен быть отфильтрован, чтобы удалить любые спектральные компоненты выше частоты Найквиста ( $ f_s$/2 ). В противном случае сигнал в зеркальной полосе создаст фантомную копию в рабочей полосе, избавиться от которой в последствии будет невозможно. Передискретизация снижает требования к порядку таких ФНЧ , как это можно видеть, сравнивая спектральные параметры для 10% ( обычный звуковой CD ) (A) и 100% ( двукратной ) передискретизации (B)

13.9.9.B Недостатки

Ограниченная полоса: Верхняя граница ∼10...100 Msps определяется тактовыми сигналами в гигагерцовом диапазоне.
Задержка: Встроенный в АЦП выходной цифровой фильтр имеет идеальную почти вертикальную заграждающую характеристику за счёт использования большого числа точек [* последовательных первичных отсчётов АЦП, участвующих в получении результата ] . И по той же причине он имеет большую задержку или «латентность», измеряемую десятками периодов выборки, т.е. в случае звуковых АЦП миллисекундами ⁸⁷.
Шум ЦАПов: Сигма-дельта ЦАПы используют аналоговые выходные фильтры, которые пропускают на выход какое-то количество цифрового шума, полностью отсутствующего в R-2R ЦАПах.
Тон паузы: АЦП с модулятором первого порядка могут создавать «тональные паузы» ( об этом ниже ), когда получают на входе постоянный сигнал ( и вызывают этим истерику среди аудиофилов ). В модуляторах более высоких порядков такой проблемы нет: шум давится за счёт действия обратных связей более высокого порядка.

==932

13.9.10 Музыкальная пауза

Одной из неприятных особенностей сигма-дельта преобразователей является возможность создания «тона пауз» - самопроизвольных внутриполосных периодических низкоуровневых ( ну, это спорно ) выходных сигналов. Этот неприятный недостаток свойственен исключительно модуляторам первого порядка, которые именно поэтому никогда не используются в серьёзной звуковой аппаратуре. Внутриполосный, т.е. попадающий в рабочую полосу сигнала, тон паузы можно получить, если подать на вход постоянный сигнал определённого уровня. Эффект исчезает при любой активности на входе, отсюда и термин «тон паузы».

Чтобы увидеть, что происходит, рассмотрим модулятор первого порядка ( рис. 13.51 ) с полной шкалой ±1V . Если ему на вход подать постоянное напряжение величиной +0.625 V и посмотреть на последовательную смену состояний, то обнаружится последовательность, показанная на рис. 13.61 . Модулятор, а значит, и битовый поток, периодически проходит по 16-тактовому циклу. Такая последовательность может быть достаточно длинной, чтобы получившийся сигнал попал в отфильтрованные выходные данные. Например, если коэффициент передискретизации в примере будет 4× , то тон паузы попадёт в середину полосы частот выходного сигнала.

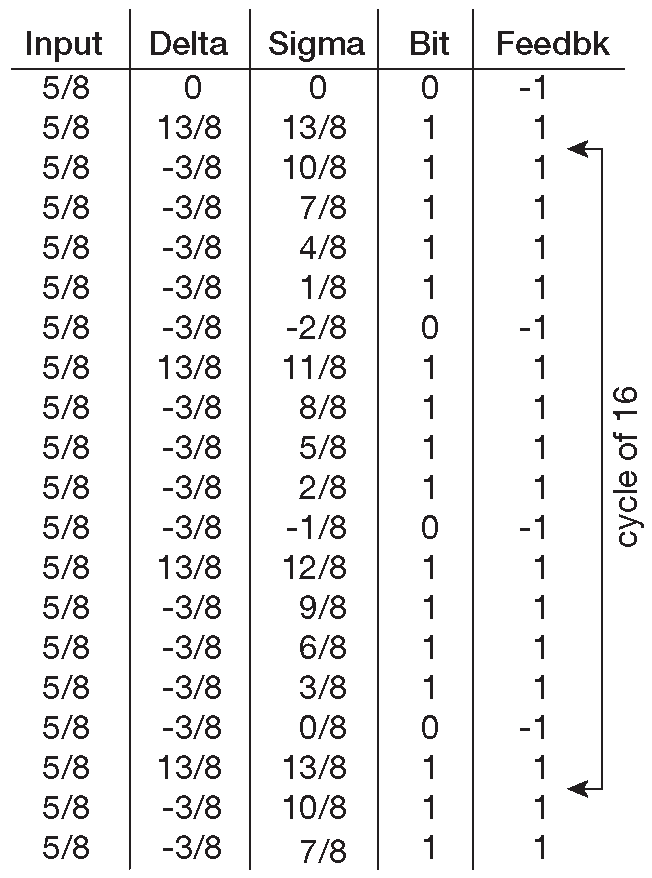
Рис. 13.61 Последовательность состояний сигма-дельта модулятора первого порядка ( рис. 13.51 ), имеющего на входе фиксированное напряжение 625 mV . «Delta» и «Sigma» - состояние входа и выхода интегратора соответственно, «Bit» - выходной битовый поток, а «Feedbk» - напряжение на выходе ЦАПа обратной связи

На рис. 13.62 дан результат моделирования ⁸⁸ двух полных периодов тона паузы. Особенно интересен выход цифрового фильтра низких частот, где синусоида тонового сигнала отчётливо видна. Её амплитуда 118 mVpp или 6% полной шкалы, т.е. тон подавлен всего на 25 dB , что совершенно неприемлемо даже для сегмента дешёвых потребительских устройств.

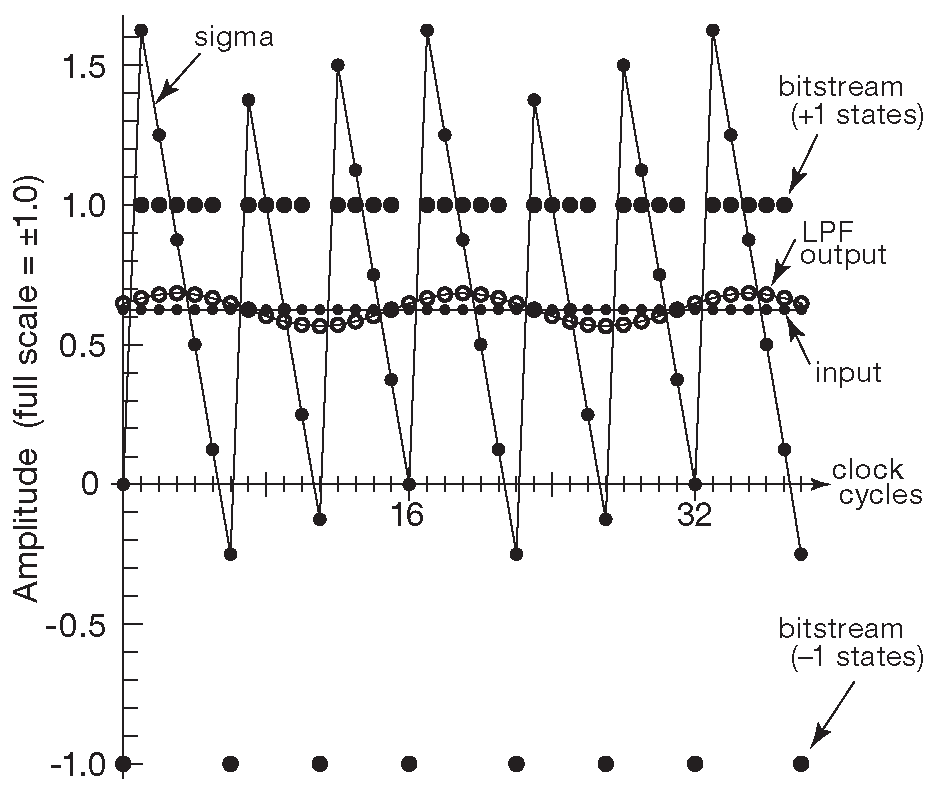
Рис. 13.62 Сигнал модулятора, совмещённый с отфильтрованным выходным сигналом, для тока паузы с рис. 13.61 . Его уровень на 25 dB ниже величины полной шкалы и попадает в середину рабочей полосы частот при 4× передискретизации

Сигма-дельта модуляторы для звуковой аппаратуры делают третьего и выше порядка, имея целью не только подавление ⁸⁹ тона паузы, но и увеличение динамического диапазона ( число эффективных разрядов преобразования ENOB ).

13.9.11 Примеры сигма-дельта схем

Всё, хватит теории! Пришло время взглянуть на несколько простеньких сигма-дельта устройств ( и чуть более сложных в §13.11 и §13.12 ). Читателю рекомендуется взять в руки соответствующие справочные материалы. Их можно взять как на сайтах производителей, так и на страничках дистрибьюторов DigiKey, Mouser или Newark.

13.9.11.A Самое простое сигма-дельта АЦП

В §13.9.1 был представлен «простейший сигма-дельта» преобразователь в виде измерителя экспозиционной дозы солнечного света. Этот пример теперь можно переделать в ΣΔ модулятор с простым накоплением потока 1-разрядных слов. Если нужно именно это, то, задействовав микроконтроллер, схему можно упростить ещё больше.

Микроконтроллеры ( Часть 15 ) - мощные гибкие устройства и в одиночку способны заменить все логические схемы из предыдущего варианта ( рис. 13.63 ). Вывод «Q» - одноразрядный порт вывода, имеющий на выходе логические уровни с потенциалами шин питания. «Ain» - вход с порогом, аналогичный по функции $U_2$ ( рис. 13.49 ). Это может быть внутренний компаратор, который часто встречается в микроконтроллерах ( рис. 13.64 ), АЦП с небольшим разрешением, также весьма распространённые, или в самом простом случае логический вход, чей не слишком точный уровень переключения вполне способен заменить здесь компаратор.

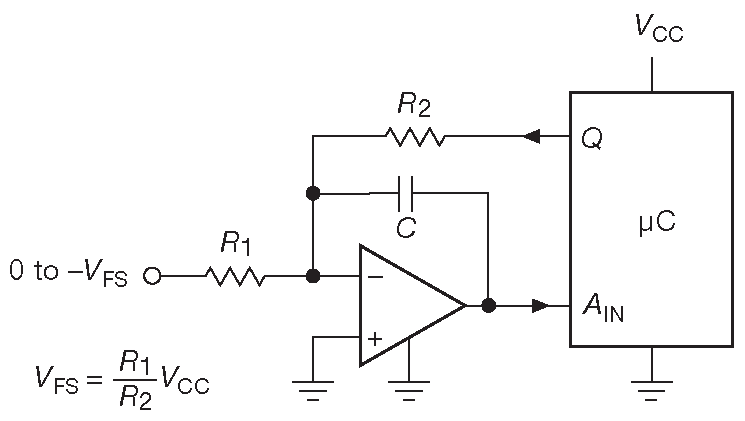
Рис. 13.63 Логическую часть сигма-дельта АЦП можно заменить микроконтроллером

==933

Имея микроконтроллер, можно написать программу, реализующую счётчик и остальную логику необходимую для работы экспонометра ( включая цифровую индикацию текущих значений и т.д. ). На более высоком уровне можно добавить цифровой фильтр, чтобы создать последовательность выходных слов, как это происходит в аппаратных АЦП. Делать всё это можно, но в большинстве случаев даже очень квалифицированные инженеры [* особенно очень квалифицированные инженеры ] просто используют отличные АЦП, которые есть на рынке и будут рассмотрены совсем скоро. В программной реализации есть опасность заставить контроллер отслеживать циклы зарядки, а именно: начать корректировать результат преобразования по данным о стабильности проводящего состояния вывода «Q» и тактовой частоты. Захочется корректировать всё это, управлять, фильтровать. В итоге программа станет слишком сложной. Данный пример нужен, чтобы показать самый схемотехнически простой вариант сигма-дельта преобразователя. Если же потребуются высокие параметры, то их всегда можно найти среди сотен готовых АЦП, имеющихся в продаже. Они недороги, и их легко использовать. Некоторые будут описаны ниже.

13.9.11.B Счётчик заряда

Вот пример преобразователя с низким потреблением и широким динамическим диапазоном, использующего микроконтроллер. Со всей возможной незамутнённостью: сначала разрабатываем конвертор, затем придумываем способ его использования. На схеме 13.64 видно, что получилось. Контроллер заряда батареи, который включён в «хододный» провод и наблюдает за степенью разряженности литиевой батареи носимого оборудования.

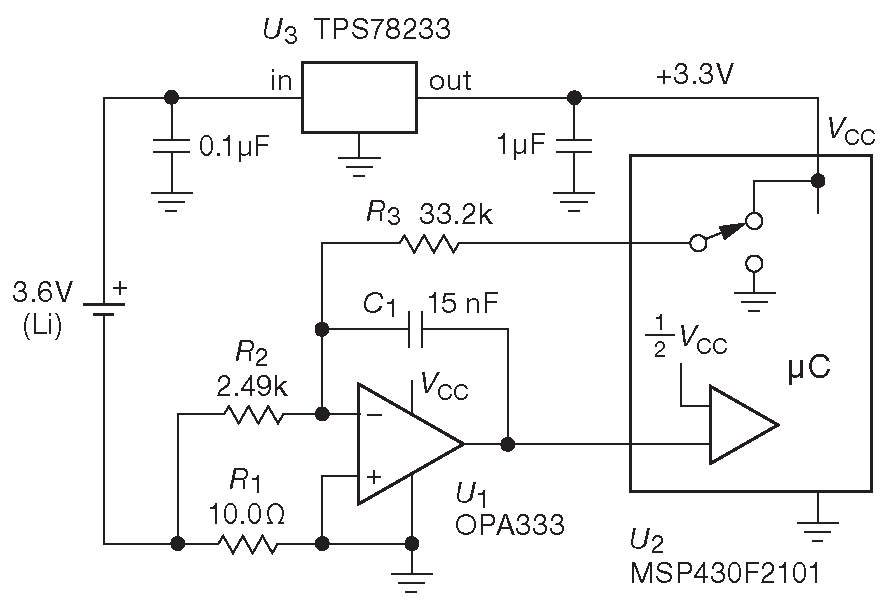
Рис. 13.64 Контроль заряда батареи с помощью ΣΔ интегратора на дискретных компонентах

Посмотрим, как он работает. Здесь использован токоизмерительный резистор небольшого номинала ( 10 Ω ). При максимальном токе нагрузки 25 mA на нём упадёт 0.25 V . Таким параметрам соответствует, например, 350-омный тензомост. Дальше выбирается ОУ: с однополярным питанием, автоподстройкой и максимальным напряжением смещения 10 μV для снижения ошибки на малых токах. В данном случае ошибка смещения эквивалентна падению на шунте при токе 1 μA (max) или динамическому диапазону 25'000 : 1 . Падение напряжения на шунте попадает на интегратор через резистор $R_2$ , для которого входной ток полной шкалы равен 100 μA ( $R_1R_2$ можно рассматривать как «делитель тока» [* , т.к. инвертирующий вход ОУ - "виртуальная земля" ] ).

Далее резистором $R_3$ устанавливается ток полной шкалы ( $I_{FS}=V_{CC}/R3$ ) , т.е. тот ток, который течёт в суммирующую точку, если ключ замкнут. И, наконец, выбором тактовой частоты ( 10 kHz ) задаётся номинал интегрирующего конденсатора $ C_1 $ таким образом, чтобы напряжение на интеграторе не могло вырасти более чем на (1/5)$ V_{CC}$ за время одного такта. Расчёт даёт номинал $ C=5/( f·R_3 )$ =15 nF .

==934

Упражнение 13.6
Покажите, что данные рассуждения верны, проведя расчёты максимального тока нагрузки, динамического диапазона и номиналов $R_2$ , $R_3$ и $ C_1 $ .

MSP430 - малопотребляющий контроллер фирмы TI. Указанная на схеме модель имеет в своём составе компаратор, на чей опорный вывод можно подавать уровень $ V_{CC}$/2 . Выходной порт переключается между уровнями земли и питания ⁹⁰. При тактовой частоте 1 MHz микросхема потребляет 0.3 mA в активном и 25 μA в малопотребляющем (mode 2 ) режимах. «Mode 2» - фактически режим «сна», в котором активен только таймер, а процессор может включиться за время одного такта. Такие свойства очень важны т.к. носимые устройства принято переводить в спящий режим для сохранения заряда батареи.

Данный «измеритель заряда» контролирует весь ток нагрузки, включая собственный ток регулятора, микроконтроллера, любой другой нагрузки на выходе регулятора и даже самого сигма-дельта интегратора. Собственное потребление определяется в основном процессором, затем идёт ОУ с автоподстройкой ( 17 μA тип. ) и стабилизатор ( 1.3 μA max ). Такая нагрузка позволяет прожить несколько месяцев на LiON батарее ёмкостью 1Ah . Остальная периферия микроконтроллера разрядит источник гораздо быстрее и должна включаться только при необходимости ⁹¹.

Отметим, что ошибка измерения тока величиной 1 μA ( из смещения ОУ для наихудшего случая ) совершенно незначительна по сравнению с током потребления системы в режиме сна. Следует заметить, что динамический диапазон для этого устройства 25'000 : 1 выглядит слегка избыточным.

13.9.11.C Три законченных сигма-дельта АЦП

Примеры сигма-дельта АЦП завершаются тремя отличными законченными преобразователями трёх разных производителей. Если этого мало, можно заглянуть в табл. 13.9 .

Maxim MAX11208B: недорогой 20-разрядный АЦП

Maxim делает компактный 10-выводной преобразователь ( рис. 13.65 ) недорогой ( $3.75 в розницу ) и тихий ( 0.7 μVrms ). Он неторопливо ( 13.75 sps ) выдаёт 20 честных разрядов разрешения при 80 dB подавления как 50-, так и 60-герцовых сетевых наводок при использовании собственного генератора ( он активируется подключение вывода «CLK» к земле ) ⁹². Полный диапазон преобразования для дифференциального сигнала ±$ V_{REF}$ при уровне синфазной составляющей от 0 до $+AV_{DD}$ . Преобразователь самостоятельно проводит калибровку усиления и смещения при включении питания, но может запустить её и по запросу достаточно необычным способом: для запуска калибровки достаточно добавить два дополнительных такта в конце обычной операции чтения данных. Как и большинство других преобразователей этот имеет отдельный вывод питания цифровой части для совместимости с низковольтовой логикой.

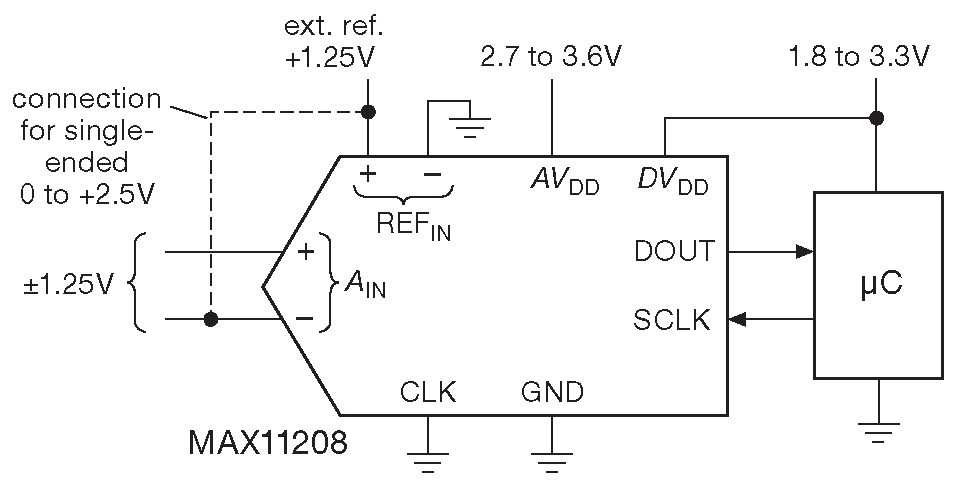
Рис. 13.65 20-разрядный АЦП с низким шумом и внутренним генератором MAX11208B фирмы Maxim. Дифференциальный вход можно включить как однополярный с диапазоном сигналов от 0 до 2$ V_{REF}$ , если подключить другой вход к $ V_{REF}$ , как показано пунктиром

Analog Devices AD7734: универсальный 24-разрядный АЦП

Эта микросхема фирмы Analog Devices - 24-разрядный преобразователь с 4-канальным входным мультиплексором ( рис. 13.66 ). У неё необычная структура входов: согласованные резисторы обеспечивают полный диапазон измеряемых сигналов ±10 V при работе от источника +5V . Кроме того есть дополнительный разряд, который расширяет диапазон измерения до 11.6 V , что позволяет проводить калибровку, имея на входе сигнал полной шкалы. Он очень спокойно переносит перегрузку по входу, допуская ±16.5 V без потери точности и ±50 V без повреждения.

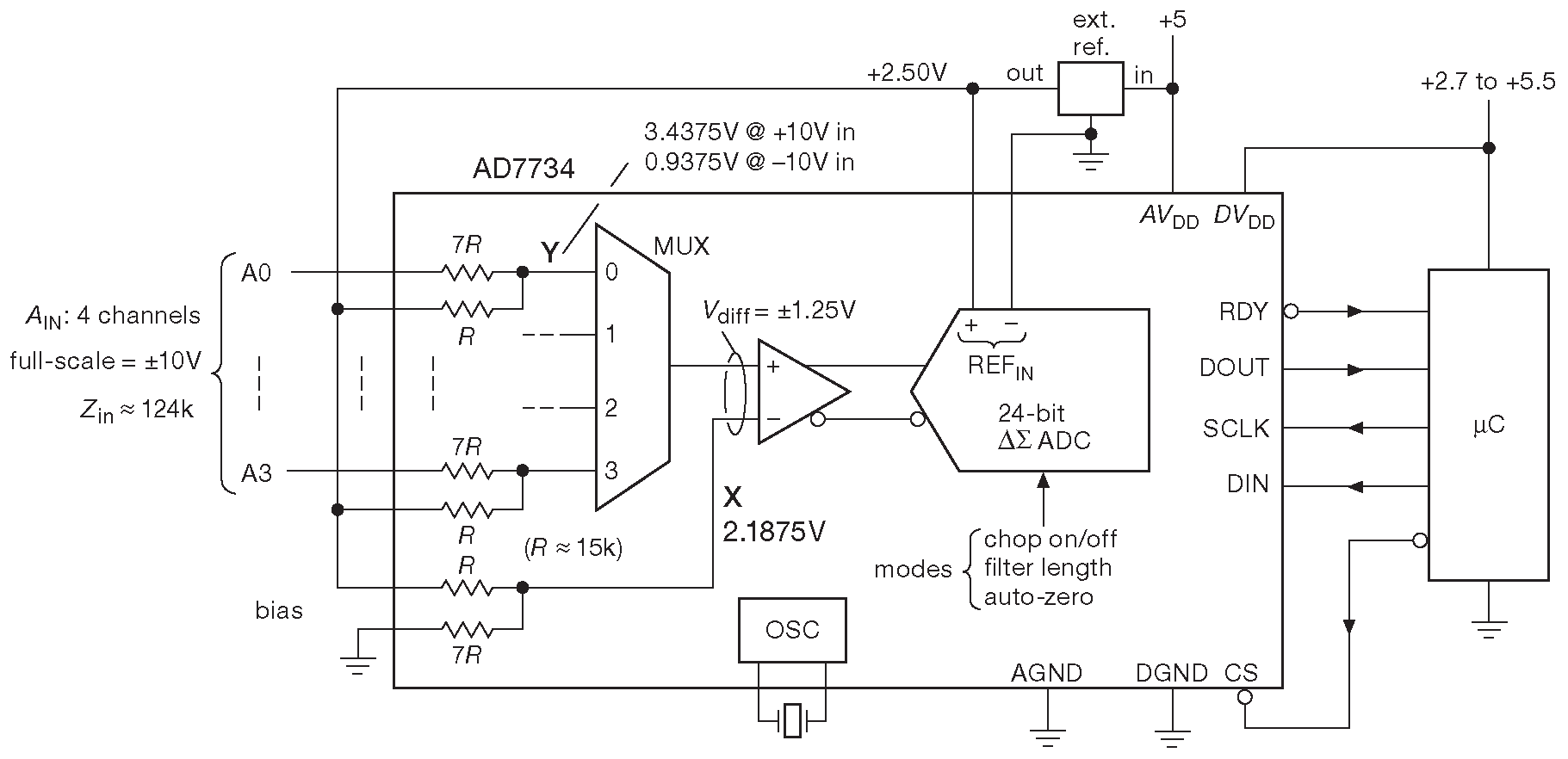
Рис. 13.66 AD7734 фирмы Analog Devices - 24-разрядный преобразователь с 4-канальным входным мультиплексором, эффективным разрешением 21 бит, широким входным диапазоном и защитой от перегрузки. С разрешения Analog Devices

==935

Процесс преобразования имеет множество настроек и позволяет выбирать длину выходного фильтра, автокалибровку нуля и режим «с прерыванием». Последний состоит из этапа реверсирования дифференциальных входов в двух соседних измерениях. Усреднение результатов таким способом позволяет избавиться от смещений в буфере и модуляторе. Такой режим с фильтром наибольшей длины даёт эффективную разрядность преобразователя 21 бит на скорости 372 sps для входных сигналов в диапазоне ±10 V . Цифра учитывает собственный шум преобразователя, который составляет 9.6 μVrms ( LSB при точности 21 бит для сигнала ±10 V составляет 10 μV ). В справочных данных приводится точность в виде « амплитудного разрешения в битах», которое для тех же условий составляет 18.1 бит. Паспортные данные оказываются консервативнее, объясняя такое положение тем, что в таблице «дана разрядность, соответствующая условию отсутствия мерцания младших битов в окрестности длиной 6 сигма». Другими словами, можно быть уверенным, что после одного измерения 18 разрядов результата будут корректны, притом, что пиковое значение шумового напряжения может быть заметно больше, чем среднеквадратическое напряжение шума $ Vrms $ ⁹³. Если среднеквадратическое напряжение шума $ Vrms $ известно , то можно рассчитать свободное от шума эффективное разрешение как ENOB$=\log_{\space 2}( V_{span}/Vrms$ ) =1.44$\space\ln( V_{span}/Vrms$ ) Вычитая из этой формулы 2.7 бита, можно получить амплитудное разрешение.

Table 13.9 Selected Delta-sigma A-to-D Convertersa Notes: (a) sorted by precision and speed; all except AD7734 have differential inputs; all have no missing codes except as noted. (b) at minimum PGA gain. (c) after calibration. (d) unused input biased at mid-supply. (e) at Vs=3.3 V. ( f) pseudo-diff’l. ( g ) external bare xtal. (h) opt ext osc input. (k ) in chopper mode. (m) min or max. (n ) 0.1 to V_-0.1 with buffers enabled. (o1 ) has neg supply, 0 to -2.6 V, with 5.25 V max total supply. (o2 ) has neg supply, 0 to -3.5 V, with 5.5 V max total supply. (o3 ) has neg supply, 0 to -6V, with 6V max total supply. ( p) 2 differential, 4 pseudo-diff'l with single common return. (q) S=SPI, P=parallel, LC= LVDS or CMOS serial. ( r ) five supplies: +5 ±5\text%, +2.5 ±5\text%, +3.15 to +5.25 ( 2x), and +1.67 to +2.7. ( s ) at max decimation. (u ) four supplies: +5 ±5\text% ( 3x), +2.5 ±5\text%. (v) 4.75-5.25 V and 1.65-2.2 V. (w) 8 diff'l, 16 single-ended ( pseudo-diff'l); (x) before cal. (y ) 2 ppm after cal. (z) 0.4 mW unbuffered. Comments: A: 16 single-ended ( pseudo-diff'l) or 8 diff'l; MUX output and ADC input pins. B: internal clk; self-cal. C: 4 single-ended (not pseudo-diff'l) or 2 diff'l; auto-shutdown in single-shot mode. D: CS5512 has ext osc; CS5510/11 = 16-bit. E: low-noise, 2.5?Vrms; auto-shutdown in single-conv mode. F: no latency; 0.8?Vrms noise; a favorite. G: bridge subsystem with offset DAC and ac excitation output. H: low-noise; opt input buffer for hi-Z; INA PGA; includes 2 curr srcs; chopper mode; auto-shutdown in single-conv mode; int ref 4 ppm/°C typ; AD7793 has fewer channels; a favorite. J: opt input buffer for hi-Z. K: low noise; 20-pin ADS1247 has 2 channels, 28-pin ADS1248 has 4 channels, both have int 10 ppm/°C ref. L: CS5534 4-ch diffl; industrial workhorse; 6 nV/\sqrt{Hz}. M: low noise. N: off-scale detectors. O: has chopper mode; AD7732 has two diff inputs. P: ADS1211 has 4 ch diff'l MUX; sample-rate boost to 312ksps; no missing codes to 22 bits. Q: low noise; pins for MUX diff'l output and ADC input. R: biopotential measurements ( EKG, EEG, etc); ADS1294=quad. S: ADS1274 = quad. T: diff'l input buffer; AD7765 to 156ksps. U: diff'l input buffer. V: pin-programmed (no registers ); LVDS or CMOS serial output. W: no missing codes to 31 bits.

==936

Это АЦП может работать на скорости 12 ksps с соответствующим снижением разрешения. Максимальный дрейф смещения и усиления ±2.5 μV/°C и ±3.2 ppm/°C соответственно. Упакован в 28-выводной корпус и стоит около $15 в розницу.

Cirrus CS5532: «промышленный» преобразователь с высокими характеристиками

Cirrus Logic ( бывшая Crystal Semiconductor ) с 1999 года выпускает CS5532-BS - 24-разрядный сигма-дельта АЦП ( рис. 13.67 ) с PGA, стабилизированным прерыванием ( коэффициенты усиления: 2, 4, 8, 16, 32 и 64 ) и очень хорошими параметрами шума, дрейфа и линейности: $e_n$ =6.4 nV/$\sqrt{Hz}$ (тип.) на 0.1 Hz при G =64 ⁹⁴, $i_n$ =1 pA/$\sqrt{Hz}$ (тип.), $Δ V_{os}$ =15 nV/°C (тип.) при G =64 , дрейф полной шкалы 2 ppm/°C (тип.) и нелинейностью ±0.0015% (max). Скорость преобразования от 6.25 sps до 3.8 ksps . В самом медленном режиме свободное от шума разрешение составляет от 20 бит ( G =64 ) до 23 бит ( G < 16 ) или, если больше нравится ENOB , то 23 и 24 разряда соответственно.

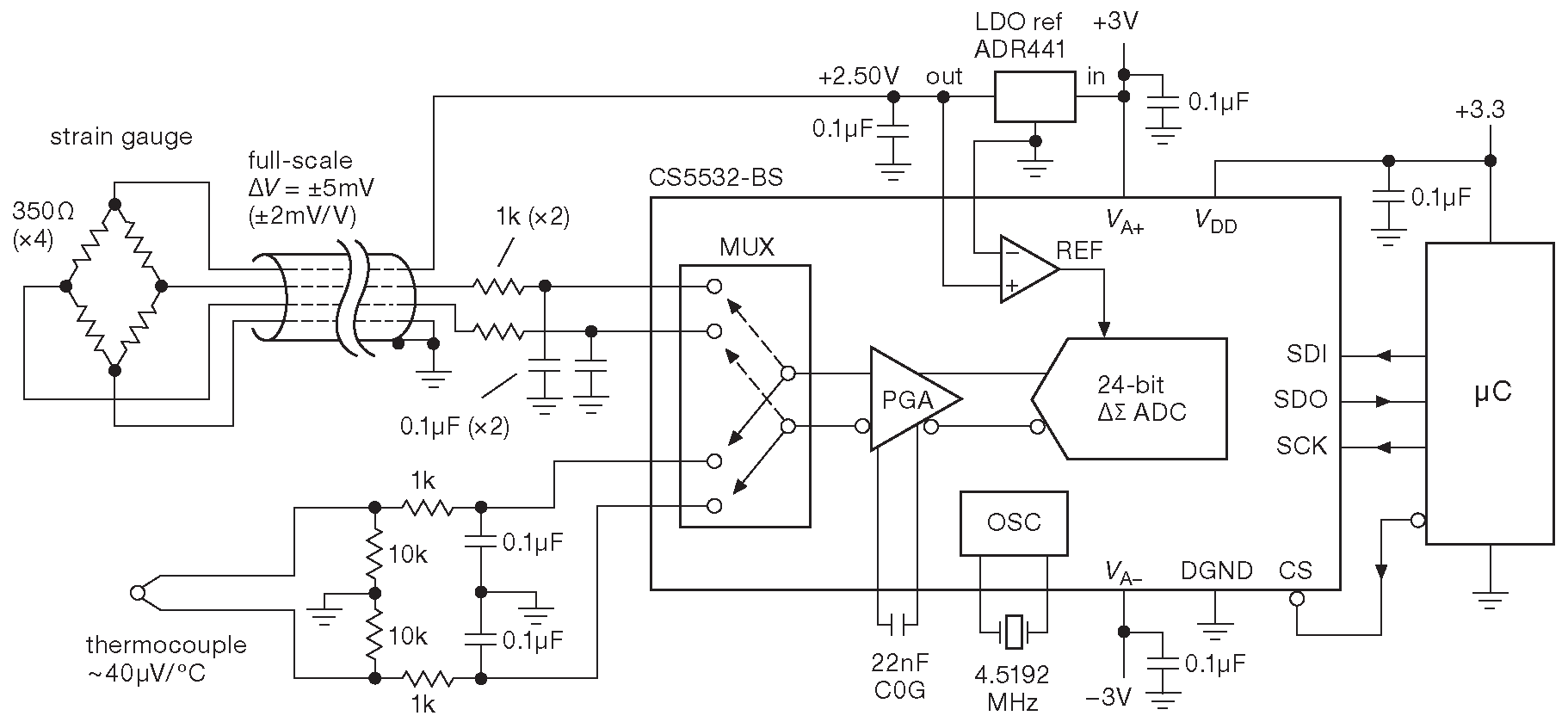
Рис. 13.67 CS5532-BS фирмы Cirrus. Прецизионный 24-разрядный АЦП. Коэффициенты усиления PGA 1, 2, 4, .. 64, но нет схемы компенсации температуры холодного спая. Такая компенсация для семи типов термопар есть в MAX31855, см. #44 в §15.8.2 и сопровождающую схему

Низкий шум, высокое усиление PGA, возможность работы от разделённого источника ±3V ⁹⁵ позволяет этому АЦП заниматься тем, для чего он, собственно, и предназначен: сигналами с термопар ( ∼40 μV/°C ) и тензомостов ( полная шкала $Δ V$ =±2 mV на каждый вольт возбуждающего напряжения ). Для коэффициента усиления G =64 полный диапазон равен ±2.5 V/64 или ±40 mV , а LSB для 20-разрядной сетки составляет 80 nV , что в 500 раз меньше, чем температурное изменение напряжения, соответствующее $Δ T$ =1°C . Аналогично, на 20-разрядном разрешении LSB соответствует 0.0008% сигнала полной шкалы с тензомоста. При таком усилении напряжение полной шакалы от указанных датчиков остаётся в пределах диапазона преобразования и дополнительного усиления тоже не требуется. Стоит $16 в розницу.

Авторы балансируют сигналы с термопар около уровня земли, чтобы минимизировать эффекты от синфазных наводок на соединительные провода, которые часто бывают неэкранированными. Для обоих видов датчиков полезно добавлять простые RC фильтры с постоянной времени 0.1 ms , чтобы подавить выбросы и защитить входы. В качестве опоры выбирается ADR441, потому что при таких питаниях нужен источник с низким падением напряжения, которому достаточно $Δ V$ =500 mV .

13.9.11.D Pro-audio ЦАПы

==937

Сигма-дельта преобразователи ( табл. 13.10 ) рекламируются профессиональным звуковым сообществом из-за сочетания разрешения, конструктивной способности противодействовать наложению спектров, естественному выдавливанию шума за пределы рабочей частоты и монотонности. Если заглянуть в какие-нибудь качественные звуковые железки, то с большой вероятностью там можно встретить схему, использующую 24-разрядный 192 ksps сигма-дельта АЦП со 128 кратной передискретизацией, и очень вероятно, что это будет микросхема Cirrus ( например, CS5381 ) или AKM ( например, AK5394A ). Данные микросхемы - долгожители, их выпускают много лет, и они являются хорошим примером разумной цены при высоком качестве.

Аудио ЦАПы используют сигма-дельта технику, но сильно отличаются от промышленных АЦП из табл. 13.10 . У них обычно низкая точность усиления ( 5...10% ) и высокое смещение ( ∼25 mV ), потому что данные цифры не играют никакой роли в звуковой технике. Вместо этого аудио-ЦАПы имеют высокую степень согласованности стереоканалов - 0.1 dB или 1% . В схеме они включаются в основном по переменному току и имеют на борту цифровой фильтр верхних частот со срезом ∼1 Hz ⁹⁶. Аудио-ЦАПы предназначены для работы на специальных звуковых скоростях и используют для вывода специальные PCM интерфейсы (I2S, TDM и т.д. ). Имеют большую, чем промышленные АЦП латентность ( задержку перед появлением выходных данных ) - от 12 до 63 интервалов выборки, причём, даже те, которые заявлены как компоненты с «низкой латентностью» ( это словосочетание означает, что задержка низкая по сравнению с каким-то конкретным временем, например, 1 ms ). Аудио-ЦАПы имеют уникальные чисто звуковые параметры: взвешенное по «кривой A» отношение сигнал-шум и данные по спектральному составу гармонических искажений.

Table 13.10 Selected Audio Delta-Sigma ADCs Notes: (a) A-weighted filter. (b) at max sample rate. (c) codec: 4 in + 6out. (d) codec: 2 in + 6 out. (e) at 48 kHz. ( f) -110 dB at 96 kHz. ( g ) consider also the PCM4420. (h) stereo codec ( ADC + DAC ) with S/PDIF to USB in/out. (k ) SNR and THD+N is with respect to full-scale; SNR is typically measured with a -60 dB input signal, processed with an A-weighted filter; THD is typically measured at 1 kHz, with a -1 dB signal.

Бесхитростная схема нормализации сигнала для аудио ЦАПов приведена на рис. 13.68 . Она взята с некоторыми изменениями из документации на отладочную плату фирмы AKM, и повторяется во множестве коммерческих устройств. ОУ 5534, похоже, является неувядающим фаворитом ( и занимает это место уже три десятилетия ) - недорогим и «достаточно хорошим». Его легко превзойти в части гармонических искажений, но для аудиофилов гораздо большее значение имеет динамический диапазон ( который определяется разрешением АЦП и уровнем шума ), а гармонические искажения с уровнем 0.001% не слышны. Для высококачественных аудио-ЦАПов предпочтительно полностью дифференциальное включение. Тема поднимается в Части _5 , см. рис. 5.70 и 5.102 ⁹⁷, а §5.14.2.E проясняет ситуацию с уровнями звуковых сигналов.

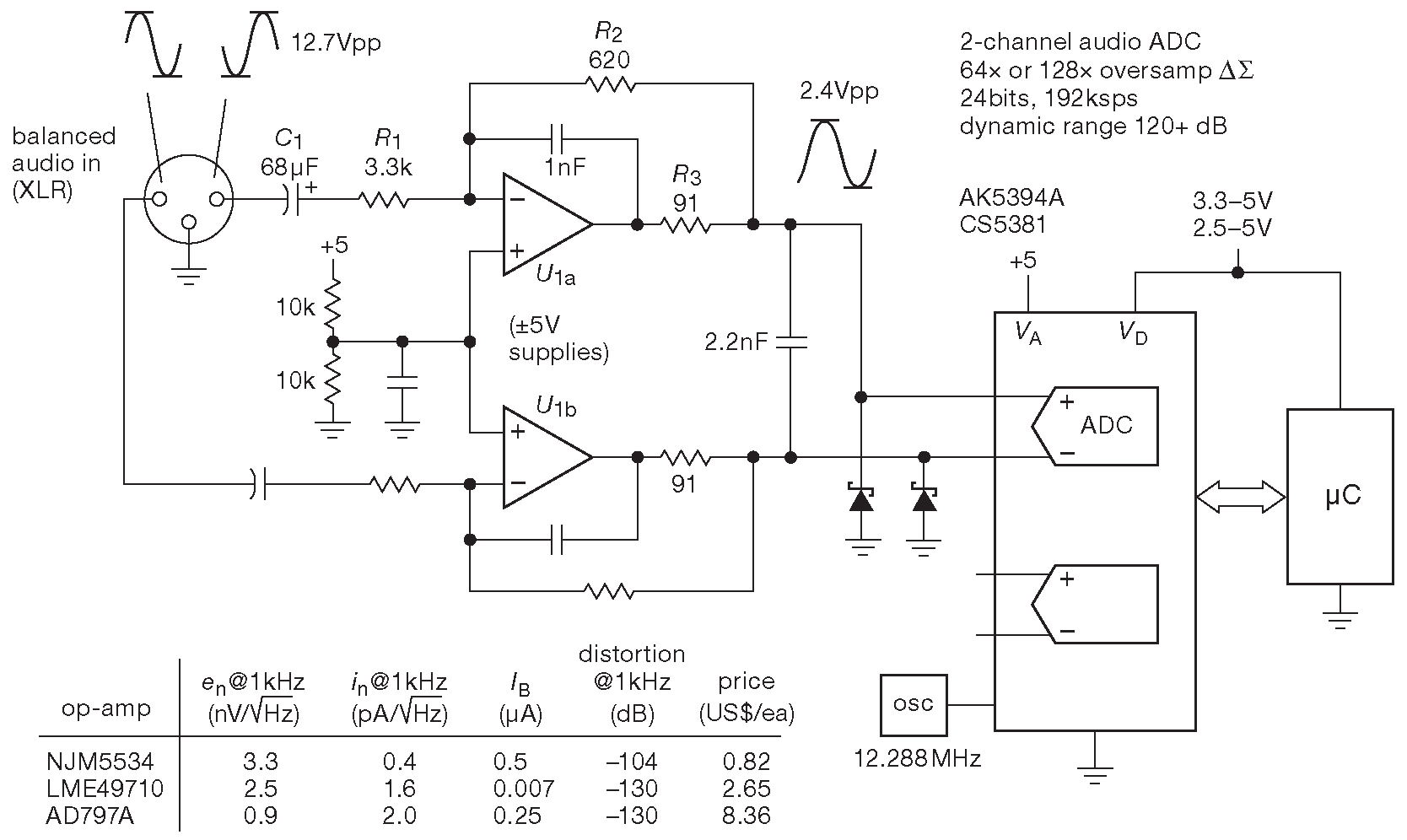
Рис. 13.68 AKM и Cirrus являются производителями непревзойдённых сигма-дельта АЦП для профессиональной аппаратуры. Обе фирмы часто используют эту простую схему для входной части, хотя полностью дифференциальный усилитель ( §5.17 ) решает задачу лучше. Воспроизводится с разрешения Asahi Kasei Microdevices, Tokyo, Japan

==937

⁸³ Талантливый во всём Джейсон Галиччо ( Jason Gallicchio), перед которым авторы в неоплатном долгу. <-

⁸⁴ Спектральные пики были собраны в группы по четыре, чтобы увеличить размер точек и упростить вывод картинки. <-

⁸⁵ Для 16-разрядного кода с дополнением до двух числа будут 0x8000 и 0x7FFF, что соответствует -32768 и +32767 , т.е. минимальному и максимальному значению. <-

⁸⁶ ФНЧ можно сделать на переключаемых конденсаторах, т.е. перейти в «дискретное» время. Такая схема использует тот же тактовый сигнал и нечувствительна к дрожанию его фронтов. <-

⁸⁷ Здесь надо отметить, что задержка получается точно такая же, как и в связке из АЦП с нулевой латентностью и входного спектрального фильтра с резкими срезами, сравнимого по параметрам с цифровыми выходными фильтрами в ΣΔ АЦП. <-

⁸⁸ Ну да, Джейсон. <-

⁸⁹ Модуляторы высокого порядка не убирают тоны пауз, но лишь снижают их амплитуду до неслышимого уровня. Вот что говорит по этому поводу авторитетный специалист по сигма-дельта преобразованиям Боб Адамс:

«Модуляторы более высоких порядков в меньшей степени склонны к зацикливанию простых последовательностей, но это тем не менее возможно. Реальную пользу они приносят подавляя шум квантования ( потому что усиление на низких частотах сильно увеличивается ), а значит, даже если модулятор решит зациклиться в последовательности какого-либо тона паузы, тон этот будет подавлен в такой степени, что почти полностью сольётся с тепловым шумом.»

⁹⁰ В контроллере есть несколько «регистров управления захватом», которые гарантируют, что временные параметры импульсов будут точны и стабильны в строгом соответствии с требованиями сигма-дельта преобразования. <-

⁹¹ Если батарея не такая большая, процессор можно переводить в спящий режим. Единственное, что при этом надо учитывать: за время сна интегратор не должен входить в насыщение. Для ∼45 μA общего потребления в состоянии сна процессор должен просыпаться каждые 80 ms , чтобы ограничить сигнал на интеграторе величиной 1V . Указанный микроконтроллер такое условие выполняет с лёгкостью, потому что способен просыпаться за 1 μs . <-

⁹² Версия с суффиксом «—A» работает со скоростью 120 sps , хуже ослабляет сетевую наводку на основной частоте, но лучше на 120 Hz и её гармониках. <-

⁹³ Справочные данные на CS5532 фирмы Cirrus объясняют данный факт так:

«Термин «свободное от шума разрешение» - это не то же самое, что «эффективное разрешение». Эффективное разрешение опирается на среднеквадратическую величину шума, а свободное от шума разрешение - на амплитудное (pp) значение шума, которое принимается за 6.6× от величины RMS шума .»

⁹⁴ Очень близко к данным на AD7190 - 8.5 nV/$\sqrt{Hz}$ . <-

⁹⁵ Двуполярное питание и двуполярный сигнал допускают: (a) 32-разрядный ADS1281 ( питание аналоговой части ±2.5 V , входной сигнал в тех же пределах ) и (b) три 24-разрядных АЦП: 16-канальны ADS1258, ADS1259 с опорным источником 2 ppm и семейство ADS1246 со встроенным PGA. <-

⁹⁶ Данный факт можно обнаружить закоротив разделяющие конденсаторы. Правда, многие из ЦАПов имеют и режим работы по постоянному току, а кое-кто ( CS5381, AK5394A и им подобные ) позволяют проводить подстройку нуля по внешней команде, что весьма удобно для очень медленных операций со связью по постоянному току. <-

⁹⁷ Интересно, что эту простую схему и недорогой '5534 используют в своих отладочных платах и AKM и Cirrus. Но в «типовой схеме включения» ( AKA “reference design”) Cirrus стоит LT1128. А TI для своего аудио ΣΔ PCM4222 использует полностью дифференциальный усилитель OPA1632. <-