13.9 (I) АЦП IV: Сигма-дельта
==922
Вот, наконец, дело дошло до самого лучшего метода аналого-цифрового ( и цифро-аналогового ) преобразования - «сигма-дельта». Это довольно сложная тема, но, разобравшись в ней, можно понять как достигаются параметры самых лучших по разрешению и точности ( например, монотонность в диапазоне 31 разряда [* двоичного ] и более ) «вольтметров» и звуковых ускорителей. Их архитектура с избыточной дискретизацией сильно упрощает входные спектральные фильтры и выполняет некоторые магические действия по удалению шума из рабочей полосы. И всё это за весьма скромные деньги. Сначала будут рассмотрены базовые принципы, а затем разобраны методы достижения гораздо более высоких параметров, нежели можно было бы ожидать. Завершается тема традиционным набором примеров.
13.9.1 Простая сигма-дельта система для подсчёта экспозиционной дозы солнечного света
Чтобы было с чего начинать, возвратимся к легенде пляжного приборостроения - мониторе экспозиционной дозы ( см. §4.8.4 , к ней придётся возвратиться ещё раз, а упокоится с миром она только в §15.2 ). Теперь экспонометр будет реализован на сигма-дельта интеграторе. Схема приведена на рис. 13.49 . Используется вариант с синхронным дозированием заряда, который работает так же, как многостадийный интегратор. Такой способ проще, потому что не использует финальный уточняющий этап: общая доза солнечного освещения набирается простым подсчётом числа тактов, в течение которых потребовалось закачивать измерительный ток ( здесь \( V_{CC}/R\) ) , чтобы уравновесить вытекающий ток фотодиода \(I_{PD}\) . Внешнее устройство сигнализирует, когда достигается установленный пользователем уровень. Сигнальная схема здесь не показана, но читатель, который знакомился с книгой последовательно, хорошо знает, как она может выглядеть.
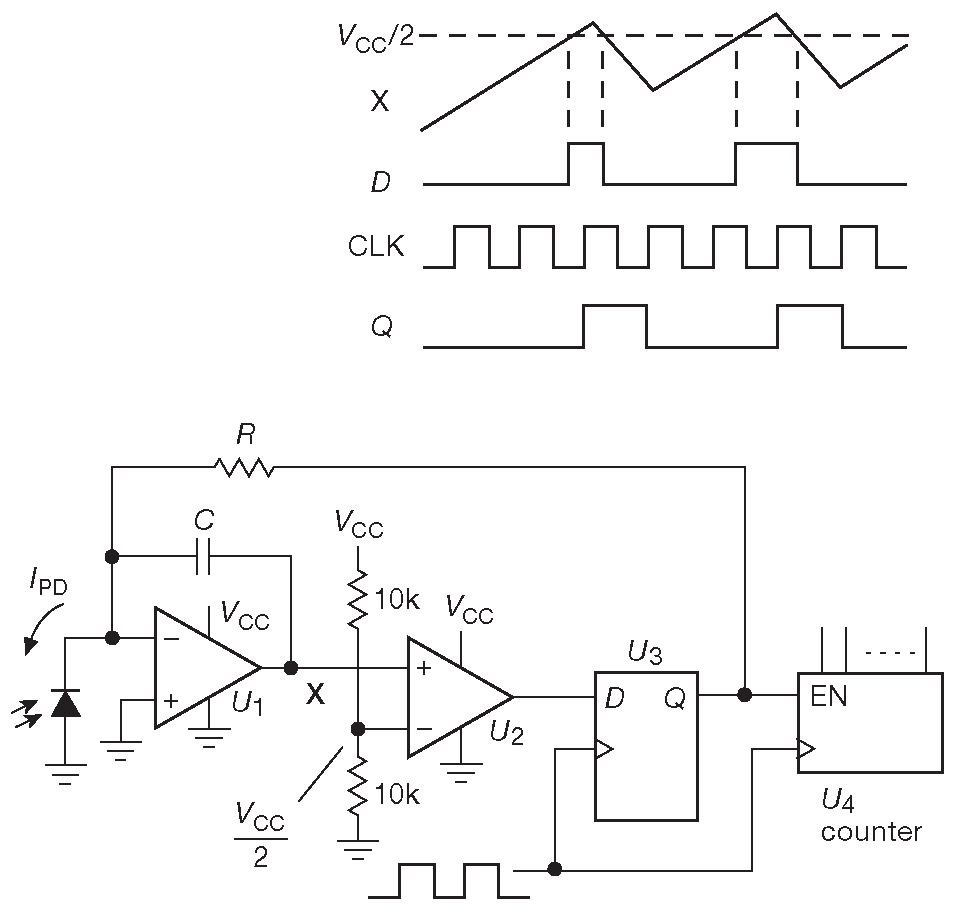
Рис. 13.49 Сигма-дельта интегратор фототока экспонометра на дискретных компонентах
Данное устройство представляет собой простейший сигма-дельта интегратор: он накапливает ( сигма ) различия ( дельта ) между аналоговым входом и образцовым током, которые складываются в суммирующей точке. Оно может стать законченным аналого-цифровым преобразователем ( а не простым интегратором ), если добавить пару блоков:
- схему сброса перед началом работы и
- элемент, считывающий показания счётчика на регулярной основе с интервалом, существенно превышающим период тактирования.
На самом деле схема может работать как АЦП и так, но на практике возможно достижение гораздо более высоких параметров, если простой счётчик заменить цифровым фильтром. Дальнейшего улучшения можно добиться каскадированием нескольких блоков «разностный усилитель - интегратор».
Все указанные улучшения будут внесены совсем скоро, но сначала надо разобраться, как работает этот простой пример.
\(U_1\) - ОУ с однополярным питанием, который может работать с сигналами вплоть до отрицательного потенциала ( и даже чуть ниже ). \(U_2\) - компаратор с активной подтяжкой. В низкоскоростных схемах, подобных представленной, можно использовать сдвоенный RRIO усилитель LMC6482, который работает от тех же +3.3 или +5V , что и цифровые схемы, и очень нравится авторам. Напряжение на выходе интегратора растёт пропорционально току фотодиода \(I_{PD}\) до тех пор, пока не превысит уровень \( V_{CC}\)/2 . После прихода очередного активного фронта напряжение на выходе интегратора начинает снижаться со скоростью, пропорциональной общему току \( ( V_{CC}/R )-I_{PD} \) . В результате активная часть периода ( D ), т.е. та часть цикла, когда его выход «Q» триггера \(U_3\) находится в состоянии ВЫСОКИЙ, усредняется по многим циклам: D\(=I_{PD}R/V_{CC}\) или \(I_{PD}=DV_{CC}/R\) . Длительность активной фазы цикла получается из числа N ( содержимого счётчика \(U_4\) ) и времени измерения T , т.е. D= N/(\( f_{clk} \) T) . Отметим, что результат не зависит от порогового напряжения компаратора ( здесь \( V_{CC}\)/2 ) или напряжения на выходе интегратора ( точка «X» ).
Ниже приводится правильная последовательность разработки.
- Выбрать период тактирования, который гораздо короче, нежели ожидаемое время экспонирования, например, \( f_{clk} \) =10 Hz . Можно и больше, но тогда потребуется более длинный счётчик.
- Выбрать номинал \(R\) так, чтобы ток через него был больше, чем предполагаемый входной ток полной шкалы: для \(I_{FS}\) =1 μA и \( V_{CC} \) =5V номинал \(R\) должен быть меньше 5 MΩ .
- Выбрать \( C \) так, чтобы изменение напряжения на выходе интегратора за время одного такта было меньше с некоторым запасом, чем уровень опорного напряжения компаратора.
==923
Для схемы 13.49 можно выбрать \( f_{clk} \) =10 Hz , \(R\) =3.3MΩ , \( C \) =100 nF , при которых напряжение в точке «X» изменяется за время одного цикла не более, чем на 1.5 V ( при минимальном \(I_{PD}\) ) , а значит, не войдёт в насыщение. Пиковая частота счёта равна тактовой частоте, а средняя скорость счёта несколько ниже ( здесь 0.6\( f_{clk} \) ) , т.е. 16-разрядного счётчика будет достаточно для накопления экспозиционной дозы, эквивалентной двум часам солнечного света.
Несколько важных моментов.
- Общая калибровка зависит от напряжения питания \( V_{CC}\) , которое считается стабильным и равным +5V . Кроме того, в схеме используется способность КМОП логики достигать уровней питания.
- Выходной сигнал интегратора не обязательно является периодическим. Он колеблется вокруг опорного уровня \( V_{CC}\)/2 , и единственное, что можно гарантировать, он изменит направление движения на следующем фронте, появившемся после пересечения уровня опорного напряжения. Такое поведение нисколько не снижает общую точность, усреднённую по множеству тактов. Метод интеграции сигма-дельта систем гарантирует их от переполнения любого вида.
- Динамический диапазон преобразователя ограничен напряжением смещения ОУ, который вызывает появление ошибки входного тока \( V_{os}/R\) . Для схемы 13.49 это 0.2 nA в худшем случае для группы «-A», т.е. динамический диапазон \(5×10\space^3\) . Входной ток ОУ ( 4 pA max при максимальной температуре ) совершенно незначителен по сравнению с величиной ошибки от смещения.
- Динамический диапазон можно сильно расширить, если заменить резистор \(R\) на переключаемый источник тока, предполагается, что входной сигнал остаётся токовым.
- Точность компаратора \(U_2\) значения не имеет. Его вообще можно выкинуть, используя в качестве порогового входной логический уровень триггера. То же самое можно сказать о точности образцового напряжения: \( V_{CC}\)/2 выбрано просто для удобства.
О некоторых дополнительных компонентах сигма-дельта преобразователей будет рассказано в §13.9.11 и нетерпеливые читатели могут сразу туда отправиться, пропустив более глубокий разбор непонятных особенностей функционирования и характеристик данной методики.
13.9.2 Всё, что вы хотели знать о сигма-дельта преобразовании, но стеснялись спросить
Как уже говорилось, сигма-дельта интегратор превращается в преобразователь среднего входного напряжения, если снимать накапливающиеся в счётчике числа на регулярной основе - с периодом \( T_{meas}\) . Естественно, для достижения приличного разрешения время измерения должно быть гораздо больше, чем период тактовой частоты, потому что максимальное накопленное число равно \( T_{meas}\space/T_{clk}\) . Это означает, что если требуется АЦП со скоростью преобразования 100 ksps ( период опроса со сбросом 10 μs ), то для частоты 10 MHz максимальное число, которое счётчик сможет накопить за 10 μs будет равно 100 , что чуть не дотягивает до 7-разрядной точности. Чтобы повысить её до 16 разрядов потребуется тактовая частота 216×100 kHz или 6.5536 GHz !
Это не вдохновляет. Идея «1-разрядного» АЦП оказалась дохлой, а весь выход - поток битов, которые можно засунуть в счётчик. Но ведь известно, что идея рабочая. Существует масса 16-разрядных сигма-дельта АЦП, оцифровывающих звуковой сигнал со скоростью 96 ksps . Есть даже 20- и более разрядные, работающие с такой частотой ( см. §13.10.1 и табл. 13.9 и 13.10 ). А как, собственно? Продолжение следует, не закрывайте книгу..
Когда-то в 1990-х рекламные материалы о бытовых CD-проигрывателях провозгласили эпоху начала использования «1-разрядных цифро-аналоговых преобразователей» так. как будто бы в сокращении разрешения с расхваливавшихся ранее 16 бит было что-то хорошее 62 . Многим тогда это казалось непонятным, но проигрыватели звучали весьма неплохо, и разбираться не хотелось.
Как сказал бы Боб Пиз ( Bob Pease ),
Что это вообще такое - «1-битный преобразователь?»
13.9.3 ΣΔ АЦП и ЦАПы
Как будет ясно из дальнейшего ΣΔ ( или ΔΣ ) преобразование может идти в любом направлении: как из D в A, так и обратно. В настоящее время ΣΔ ЦАПы используются в первую очередь в звуковой области, где очень важна их отличная линейность, монотонность и низкая цена. Типовой звуковой ΣΔ ЦАП может иметь шесть 24-разрядных 192 ksps каналов с эффективным динамическим диапазоном 114 dB всего за $10 63 . А ΣΔ АЦП закрывают широкий спектр применений от точных 24-разрядных медленных преобразователей до звуковых АЦП высокого разрешения ( 24 бита, 96 ksps ) и быстрых преобразователей с невероятными параметрами ( 16 разрядов 20 Msps ).
==924
В дальнейшей дискуссии говорится преимущественно о ΣΔ АЦП как из-за их важности, так и из-за того, что в их конструкции находят применение близкие к идеальным цифровые фильтры.
На этом пути придётся разобраться с вопросом, напоминающим большой розыгрыш, а именно:
«Как получается, что 1-разрядное преобразование, идущее с несколько более высокой скоростью дискретизации ( скажем, в 64 раза большей, чем обычный предел Найквиста 2\( f_{max} \) ) даёт на выходе цифровой код высокой точности, например, 16 разрядов? »
Мысль можно сформулировать иначе: от 1-разрядного преобразования с 64-кратной избыточной передискретизацией можно ожидать итогового цифрового кода с разрядностью 6 бит ( 26 =64 ), не больше 64 . Дальше станет ясно, что это не просто возможно, но что можно достичь гораздо лучшего результата ( именно это требуется в обработке звука ) 65 .
13.9.4 Собственно процесс ΣΔ преобразования
Базовые этапы ΣΔ преобразования показаны на рис. 13.50 . Входной сигнал с полосой, ограниченной частотой \( f_{max} \) ( обычно это делается спектральным фильтром 66 ), преобразуется в битовый поток 67 с помощью модулятора. Этот последний тактируется с частотой, кратной частоте предела Найквиста 2\( f_{max} \) , и даёт на выходе поток с частотой \( f_{bit}\) = OSR × 2\( f_{max} \) , где OSR - коэффициент передискретизации . Битовый поток является только промежуточным этапом на пути получения результата: его ещё необходимо пропустить через ФНЧ.

Рис. 13.50 Сигма-дельта преобразователи безразлично A/D или D/A состоят из двух частей: модулятора с избыточной дискретизацией, который создаёт промежуточный поток битов, за которым следует ФНЧ, который восстанавливает преобразованный сигнал
Отметим, что и модулятор, и ФНЧ могут быть как аналоговыми, так и цифровыми. Тип зависит от конвертора: сигма-дельта АЦП состоит из аналогового модулятора и цифрового фильтра, а ЦАП - из цифрового модулятора и аналогового фильтра 68 . Из сказанного следует, что сначала будет рассмотрен модулятор.
13.9.4.A Модулятор
==925
Так или иначе, но ФНЧ - это «просто фильтр», который ограничивает полосу входного сигнала 69 . Всё самое интересное ( и загадочное ) творится в модуляторе. На рис. 13.51 приведена блок-схема передискретизирующего модулятора «первого порядка», который получает на входе аналоговый сигнал амплитудой от –1 до +1V , лежащий в полосе с верхней границей \( f_{max} \) и создающий 1-разрядный битовый поток с частотой в OSR раз большей, чем предел Найквиста 2\( f_{max} \) .
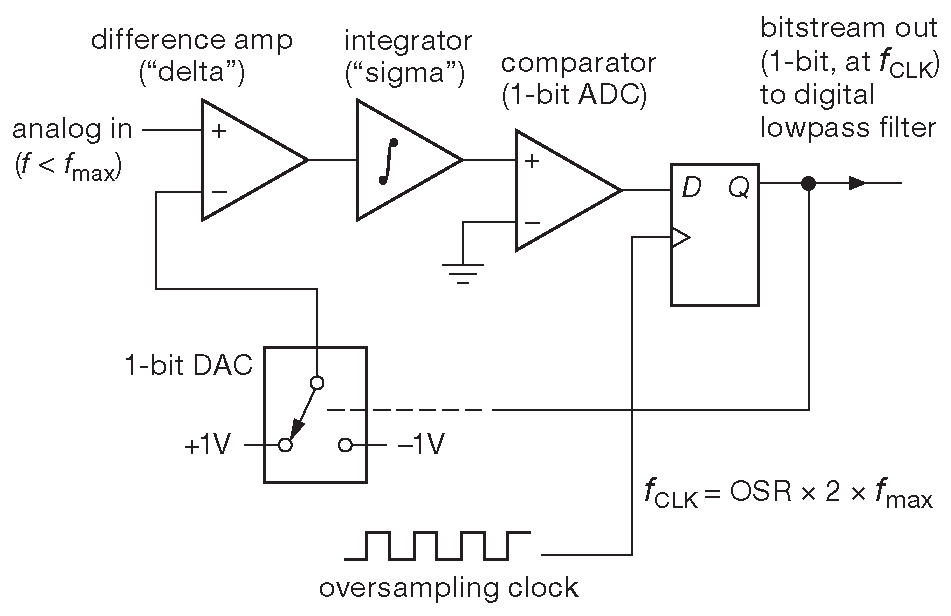
Рис. 13.51 Аналоговый сигма-дельта модулятор первого порядка
В каждом цикле тактовой частоты текущее значение битовой последовательности, преобразованное в аналоговое напряжение ( здесь ±1V ), вычитается из входного сигнала, а разница интегрируется ( самым обычным аналоговым интегратором, в данном случае неинвертирующим ) и подаётся на компаратор с запоминанием. Усиление в интеграторе выбирается так, чтобы для сигнала полной шкалы на входе ( здесь +1V ) изменение выходного уровня за время одного периода тактовой частоты равнялось напряжению полной шкалы ( +1V ). Таким образом, интегратор можно рассматривать как «аналоговый аккумулятор»: для фиксированного входного напряжения \( V \) его выход увеличивается на \( V \) за один период тактового сигнала.
В результате получается быстрый поток нулей и единиц ( на частоте, скажем, в 64 раза большей, чем обычная частота выборки 2\( f_{max} \) ) , соответствующий относительно медленному ( в данном случае как минимум в 64 раза медленнее ) изменению входного сигнала. Если условиться, что биты имеют уровень ±1V , получаем, что модулятор создаёт поток, чьё среднее значение соответствует входному сигналу. Данную схему можно рассматривать как петлю отрицательной обратной связи, которая стремится минимизировать среднюю ( т.е. интегральную ) ошибку между входным сигналом и выходным потоком ( сравнение идёт в аналоговой форме, благодаря обратному преобразованию потока с помощью «1-разрядного ЦАПа» ). Если взглянуть на схему внимательнее, то можно обнаружить, что происходит совершенно ужасная вещь: такт за тактом входной поток просто мечется между двумя предельными уровнями. Как точно заметил Боб Адамс 70 : «Передискретизирующие преобразователи увеличивают разрешение не путём уменьшения ошибки между аналоговым входом и цифровым выходом, а заставляя ошибку появляться чаще.»
13.9.4.B Динамический диапазон ( разрешение ) АЦП
Выходной цифровой ФНЧ создаёт цифровые n-разрядные числа, которые выводятся наружу. Используются обычно КИХ ( FIR ) фильтры ( см. рис. 13.52 ). В этом случае 1-разрядный сдвиговый регистр с проходящими сквозь него единицами и нулями включает и выключает набор постоянных коэффициентов 71 , которые суммируются с данными, получая в итоге n-разрядные выходные значения. Из-за того, что данные выходят из фильтра со скоростью передискретизации [* т.е. в OSR раз быстрее, чем надо ] их приходится подвергать прореживанию. Проще всего просто выкинуть лишние значения, оставляя только одно число на OSR тактов ( «##децимация» ) 72 .
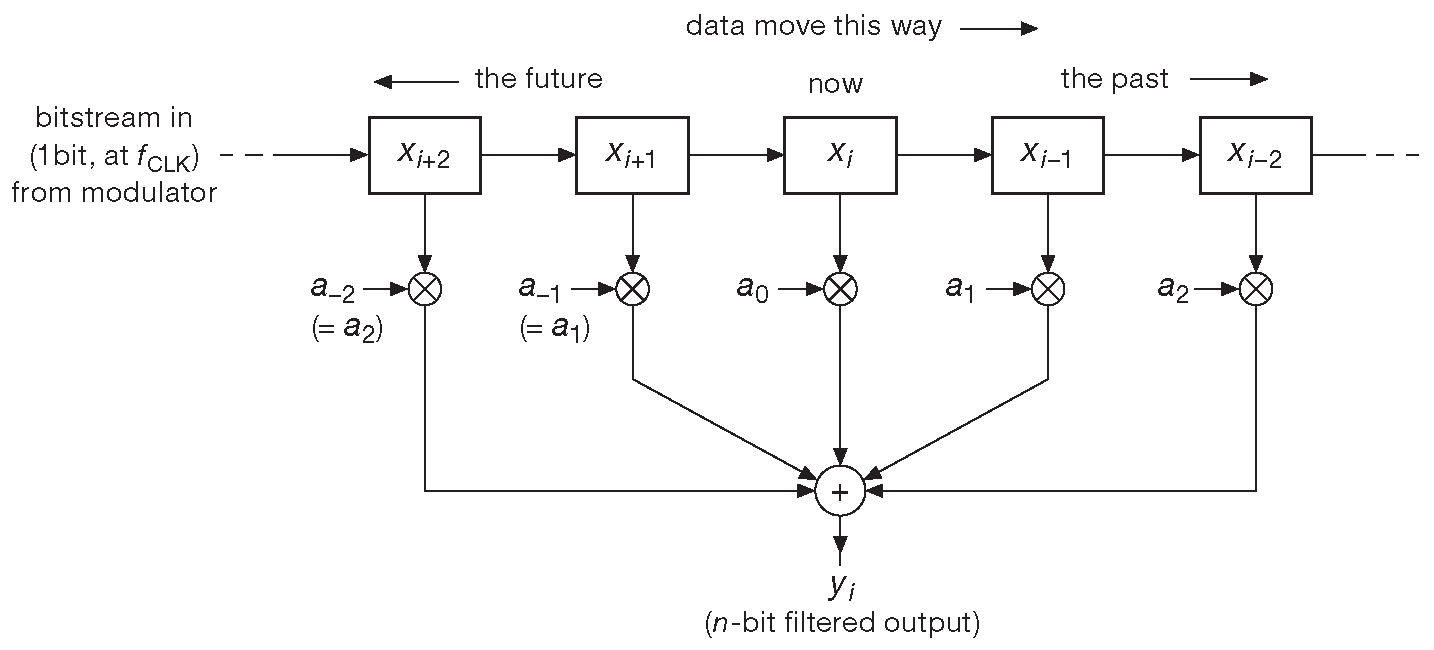
Рис. 13.52 Цифровые фильтры используют память и арифметические схемы для преобразования входной цифровой последовательности в выходную фильтрованную и тоже цифровую версию ( см. §6.3.7 ). Сдвиговый регистр, умножитель и сумматор образуют симметричный рекурсивный ( КИХ ) фильтр, который подходит в качестве выходного ФНЧ для 1-разрядного сигма-дельта АЦП
Если подойти к вопросу прямолинейно, то увеличение разрешения достигается усреднением массы 1-разрядных значений на каждой половине цикла наибольшей частоты входного спектра. Усреднённое значение битового поток отслеживает входной сигнал, и эта картина соответствует описанию Боба Адамса, а значит, всё хорошо.
Или не совсем? Рассмотрим пример: предположим, что оцифровывается звук с частотой \( f_{max} \) =20 kHz . Обычное АЦП ( например, последовательного приближения ) может работать со скоростью 48 ksps , оставляя удобный запас над предельной частотой 40 kHz . Теперь возьмём ΣΔ АЦП с типичным коэффициентом передискретизации 64 , т.е. модулятор крутится на 64×48 kHz = 3.072 Msps , создавая 1-разрядный битовый поток с такой же скоростью. Фильтруем этот поток, допустим, фильтром «скользящего среднего» 73 . Цифровая фильтрация обрабатывает 64 последовательных бита одновременно. На что будет похож выход? Это просто. Когда усредняется 64 бита, на выходе может получиться только 64 65 возможных значений, т.е. в итоге получилось АЦП с разрядностью жалких 6 бит. [* Каждый бит - отдельное значение, следовательно, усредняя сложением 64 однобитовых числа, получаем: если на входе все нули, выход =0 , если все единицы =64 . С мест поправляют : если есть состояния «0» и «64» , то всего состояний 65 ].
Следуя той же схеме, чтобы достичь 16-разрядной точности, требуется обработать 216 = 65536 значений, что потребует выборки со скоростью приблизительно 3 гигагерца ! Сигма-дельта преобразование, оказывается, не такая хорошая штука.
==926
13.9.4.C Что же происходит на самом деле? ( Рассмотрение во временной области )
Ответ на парадокс можно дать несколькими способами. В литературе по теме обычно говорится, что работа схемы квантования имеет две составляющие: идеальное преобразование и привнесение широкополосного «шума» ( он состоит из разницы между реальным аналоговым сигналом и копией, восстановленной из получившейся 1-разрядной последовательности ). Этот «привнесённый шум квантования» имеет широкий спектр ( спасибо высокой частоте передискретизации ), который заходит вверх за частоту тактирования. Важнее всего в этом процессе то, что шум квантования ( который так и остаётся в выходных данных ) минимален на низких частотах и растёт на высоких. Благодаря процессу модуляции большая его часть находится сильно выше \( f_{max} \) . [* Полоса преобразования в 64 раза шире, чем 2\( f_{max} \) , а следовательно, даже при равномерном распределении шума в полосу сигнала с границей \( f_{max} \) попадёт 1/128 от общего шума квантования ] . Такой спектральный состав позволяет выходному ФНЧ работать селективным подавителем большей части шума квантования в выходном потоке, сохраняя сам преобразованный сигнал. В итоге имеем гораздо большее разрешение и динамический диапазон, чем ожидалось при «тупом» рассмотрении процесса.
Приведённые выше рассуждения достаточно корректны, но не вполне удовлетворительны ( и поэтому тема вновь будет поднята в §13.9.5 ). Авторам хотелось рассмотреть секреты динамического диапазона АЦП во временной области, не затрагивая частотную. Но в данном месте вышла некоторая заминка. Чтение опусов с названиями «Сигма-дельта АЦП раскрывают тайны» и «Сигма-дельта АЦП для идиотов» не помогло. Все такие публикации имеют слабое место: «..сигма-дельта преобразователи преодолевают данное ограничение с помощью техники сдвига шума..» и «..можно увидеть, как модулятор сдвигает шум в область высоких частот, позволяя получить более высокое разрешение» ( выдержки из обеих указанных статей ).
Вот как можно объяснить всё это в терминах временной области 74 . Во-первых, ФНЧ не просто усредняет серию импульсов из живого битового потока. Вместо этого, он взвешивает каждое 1-разрядное значение с аккуратно подобранным коэффициентами, чтобы достичь наилучших параметров фильтрации ( см. §6.3.7.D ). Из-за того, что отдельные отсчёты получают различный вес, появляется гораздо больше вариантов, чем просто 64 значения как в примере выше. Более того, типичный КИХ фильтр взвешивает и суммирует гораздо больше отсчётов и за гораздо большее время, чем период частоты передискретизации, т.е. уходя далеко за «интервал Найквиста» ( под которым подразумевается половина периода частоты \( f_{max} \) ) . Для 64-кратной передискретизации можно использовать цифровую фильтрацию по тысячам точек ( отдельным последовательным значениям внутри битового потока ) каждый со своим множителем, размазывая каждый по десяткам интервалов Найквиста, чтобы получить в итоге окончательное ( прореженное ) число. Такой вариант достижения высоких разрешений как минимум несколько правдоподобнее, чем простое усреднение.
Продолжая в том же ключе, то, что каждый бит потока влияет на много прореженных итоговых n-разрядных выходных слов, ничего не означает. С конспирологической точки зрения, вполне правдоподобна версия, что модулятор столь умно придуман, что может создавать такой поток битов, который после прохождения через фильтр нижних частот от преобразуется в n-разрядные выходные числа с очень сильно улучшенным динамическим диапазоном. То есть, не будет большой ошибкой 75 сказать, что «всё дело в волшебном модуляторе». Но тогда вопрос надо ставить иначе: «Как столь примитивная железка ( рис. 13.51 ) может решать столь сложную задачу?»
==927
13.9.5 Некоторые пояснения к «перераспределению шума»
Как уже отмечалось, обычно при описании сигма-дельта преобразователей говорят о «перераспределении шума» в частотной области. «Шум квантования» с плоским спектром, появляющийся в дискретизаторе ( компаратор на рис. 13.51 ) «выдавливается» в область высших частот, по большей части в зону за пределами частоты выборки, а меньшее количество внутриполосного шума ведёт к увеличению точности. Вот, собственно, и все объяснения.
Для многих инженеров таких объяснений оказывается вполне достаточно. Но даже если лично вы ими прониклись, всё же будет лучше разобрать имеющиеся аргументы. Самая простая схема показана на рис. 13.53 . Здесь модулятор собран на аналоговом интеграторе и преобразует непрерывный аналоговый вход в двухуровневый аналоговый же выход ( ±1V ). В этой модели 1-разрядный дискриминатор ( компаратор ) заменён на внешний источник шума квантования \( V_{qn}\) , чей спектр простирается за границу частоты передискретизации 76 . Интегратор здесь стоит в прямой ветви распространения входного сигнала ( отсюда ФНЧ ), но в ветви обратной связи для шума ( отсюда ФВЧ ) 77 . Для этой простой аналоговой петли нетрудно вывести параметры частотного отклика как входного сигнала, так и шума квантования. Здесь имеется только один масштабирующий элемент - интегратор, чьё усиление можно записать как G =\(ω_0/(jω)\) ; т.е. усиление интегратора пропорционально 1/\(ω\) и снижается до единицы на частоте \(ω_0\) . Из предыдущего обсуждения \( ω_0≈1/( 2πf_{overclock}\space ) \) , т.е. равна частоте передискретизации конвертора.
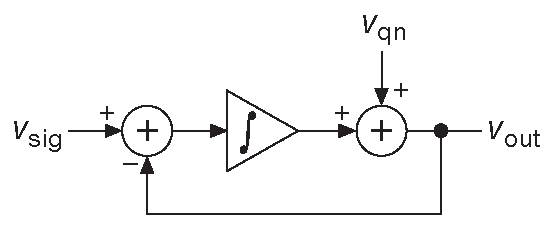
Рис. 13.53 Модель, объясняющая шум в сигма-дельта АЦП первого порядка. Используются только аналоговые компоненты, а дискриминатор заменён внешним источником шума квантования
Теперь можно вывести усиление, для которого потребуются комплексные числа. Чтобы получить усиление для сигнала \( G_{sig}\) , полагаем \( V_{qn}\) =0 , тогда: \[ V_{out}=\frac{ω_0}{jω}( V_{sig}-V_{out}), \] или \[ \frac{V_{out}}{V_{sig}}=\cfrac{\cfrac{ω_0}{jω}}{\cfrac{1+ω_0}{jω}}, \] тогда \[ |G_{sig}|≡\left|\frac{V_{out}}{V_{sig}}\right|=\frac{1}{\sqrt{1+(ω/ω_0 )^2}} \]
Получили уравнение фильтра нижних частот с частотой среза на \(ω=2πf=ω_0\) ( рис. 13.54 ) 78 .
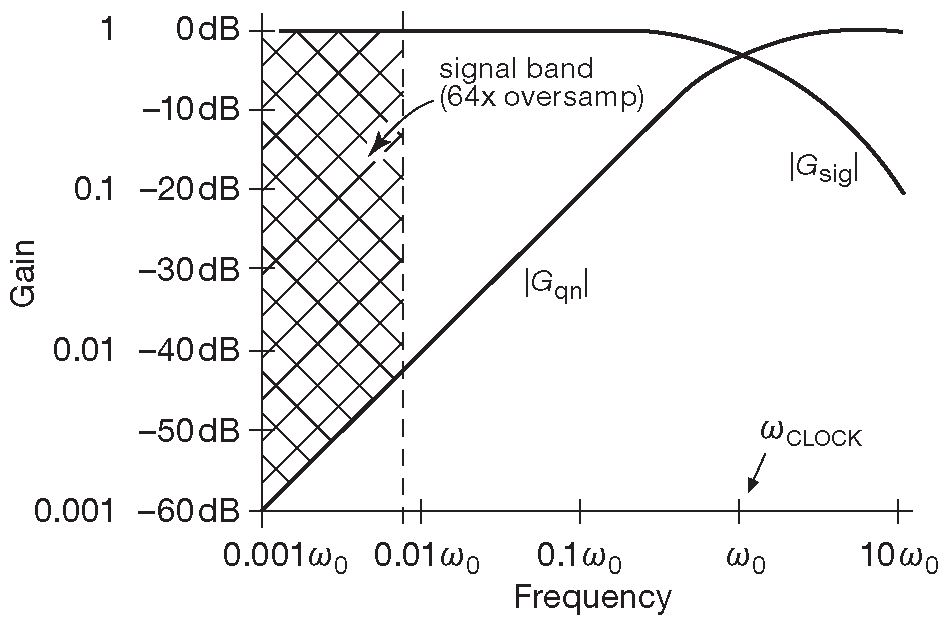
Рис. 13.54 АЧХ сигнала и шума квантования для сигма-дельта АЦП первого порядка. Частота тактирования \(ω_{clk} = ω_0 \) = OSR·2·\(ω_{max}\) , здесь равна 128 \(ω_{max}\)
Аналогичным образом выясняем усиление по шуму квантования \( G_{qn}\) , приравнивая \( V_{sig}\) =0 и получая: \[ V_{out}=V_{qn}-\frac{ω_0}{jω}V_{out} \] или \[ \frac{V_{out}}{V_{qn}}=\frac{1}{1+\cfrac{ω_0}{jω}}, \] тогда \[ |G_{qn}|≡\left|\frac{V_{out}}{V_{qn}}\right|=\frac{ω/ω_0}{\sqrt{1+(ω/ω_0 )^2}}. \]
Это уже фильтр высоких частот с той же частотой среза 79 .
==928
Итак, в сигма-дельта АЦП первого порядка шум квантования ослабляется на низких частотах, его спектр линейно расширяется вплоть до частоты передискретизации. Но частота-то избыточная, т.е. интересующий пользователя спектр расположен в низкочастотном углу ( и занимает полосу согласно степени передискретизации ). Другими словами, большая часть шума квантования лежит за пределами полосы сигнала. В модуляторах высоких порядков данный эффект проявляется отчётливее: график шума в модуляторе второго порядка квадратичный, кубический для третьего и т.д. Отсюда и процитированное заключение: «Сигма-дельта АЦП достигают такой точности, выдавливая шум в область высоких частот» 80 . Возможно, формулы не слишком возбуждают, но, по крайней мере, они показывают, что происходит в простой и однозначной форме.
13.9.6 Итоги
И из правдоподобных аргументов во временной области, и из прямых расчётов в частотной выходит, что модулятор является ключом к высоким параметрам сигма-дельта АЦП. В их число входит способность оцифровывать аналоговый сигнал с разрешением заметно более высоким, чем коэффициент передискретизации. Более того, данный показатель качества ( ENOB/(\(\log_{\space 2}\)OSR) , где ENOB - эффективное число бит в оцифрованном сигнале ) растёт по мере роста сложности модулятора. Современные АЦП используют модуляторы «высоких порядков», что означает, единственный разностный усилитель и интегратор заменяется несколькими последовательными звеньями из разностного усилителя и интегратора каждое. Все звенья используют общий битовый поток ( рис. 13.55 ) 81 . Модуляторы высоких порядков находят широкое применение, потому что расширяют динамический диапазон без увеличения коэффициента передискретизации. Кроме того, они в большей степени подавляют тон паузы ( см. §13.9.9 и §13.9.10 ), которые портят жизнь модуляторам первого порядка.
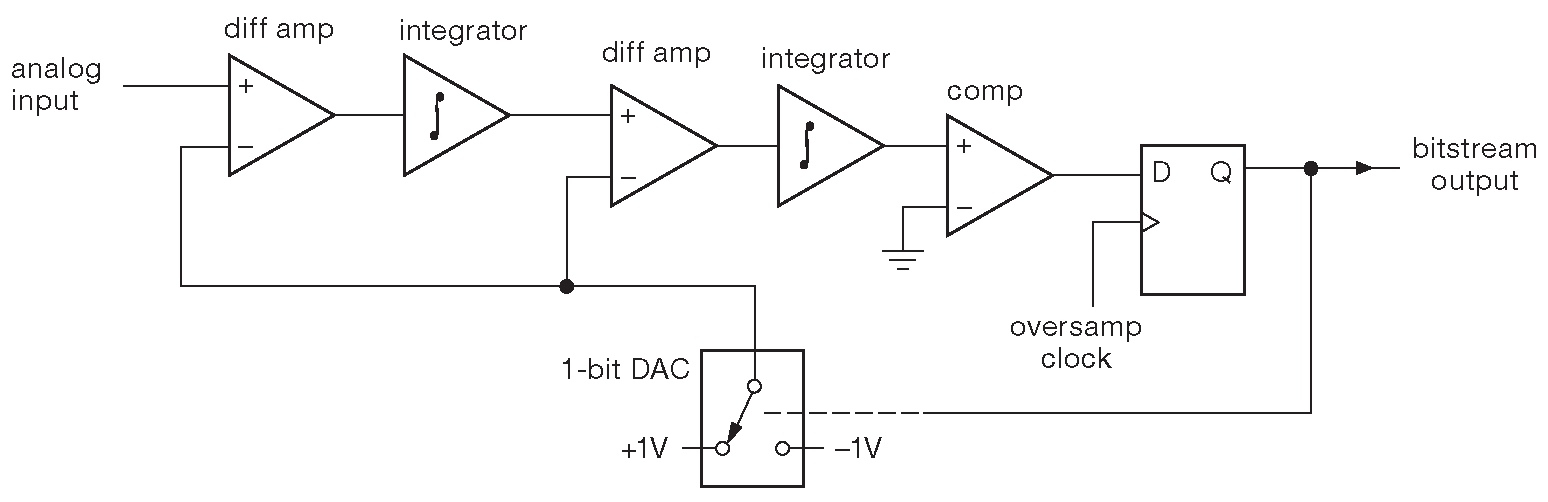
Рис. 13.55 Аналоговый сигма-дельта модулятор второго порядка. Один или оба интегратора можно заменить на ФНЧ
Хотя рассуждения о временной области могут быть полезны ( разве что для обоснования заявленного отличного динамического диапазона ), любая серьёзная аналитика должна использовать рассмотрение в частотном диапазоне. Последний показывает, что модуляторы высоких порядков ( собранные на m интеграторах ) изменяют спектр шума так, что внутриполосный шум квантования ( от постоянного тока до \( f_{max} \) ) подавляется в степени OSR [m+0.5] , где m - порядок модулятора ( для схемы 13.51 m=1 ). Или иначе, каждое удвоение коэффициента передискретизации снижает шум квантования в такой степени, как если бы динамический диапазон увеличился на m+1/2 бита. Или, используя терминологию порядка модулятора, эффективное число разрядов ( ENOB ) равно \(\log_{\space 2}\) от коэффициента передискретизации ( 6 для OSR=64 ), умноженному на m+1/2 ( т.е. для модулятора второго порядка и OSR=64 имеем ENOB ≈ 15 бит ). [* Т.е. ENOB \(=\log_{\space 2}\)(OSR [m+0.5]) = [m+0.5] \(\log_{\space 2}\)(OSR) ] . График 13.56 показывает теоретически возможный динамический диапазон сигма-дельта АЦП как функцию от коэффициента передискретизации и порядка модулятора 82 .
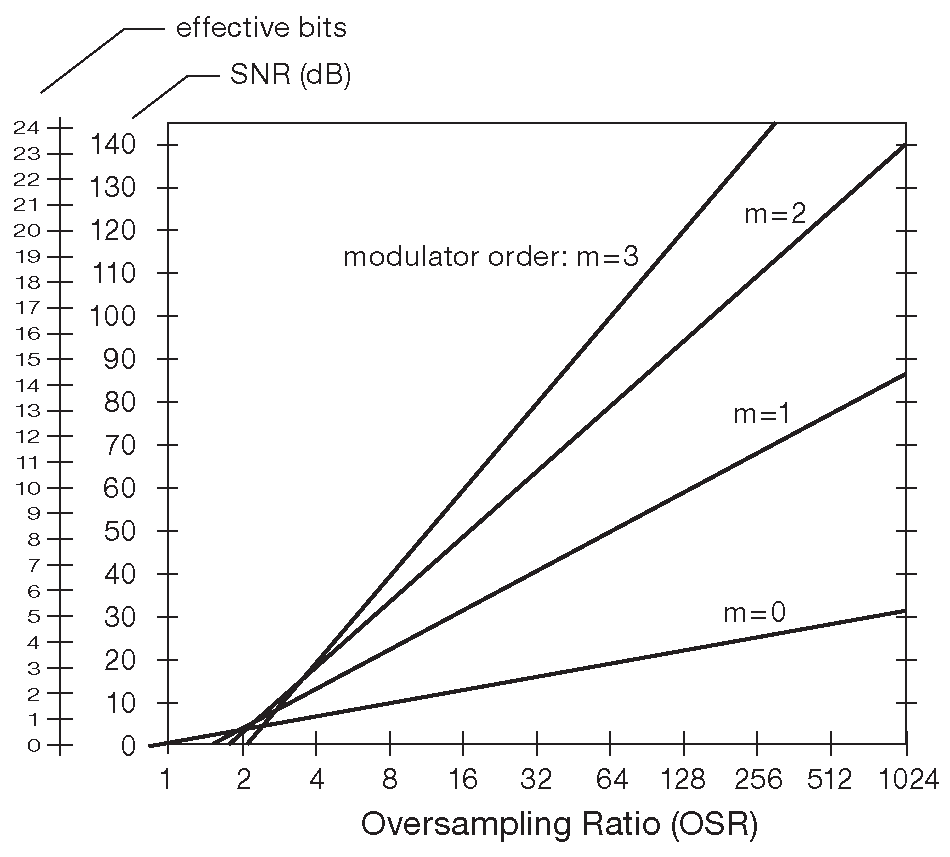
Рис. 13.56 Динамический диапазон ( SNR ) и число эффективных разрядов ( ENOB ) как функции коэффициента передискретизации ( OSR ) и порядка модулятора ( m ) для 1-разрядного АЦП с передискретизацией ( для 2-разрядного варианта наклон идёт в два раза круче )
Другим способом увеличения динамического диапазона, скорости или обоих параметров разом является построение модулятора, создающего поток «слов», каждое из которых имеет разрядность больше одного бита. На рис. 13.51 приводится пример 1-разрядного АЦП, 1-разрядного ЦАПа и 1-разрядного регистра, каждый из которых должен быть заменён на 2-разрядный эквивалент ( четырёхуровневая система ). Есть масса остроумных ухищрений, исправляющих недостатки многоразрядных модуляторов ( например, циклический сдвиг битов слова для усреднения нелинейностей, вызванных смещением ), но все эти вопросы выходят за рамки данной книги.
==928
62 Эхо от тех фанфар гуляет до сих пор. Вот современный пример:
«Какой-либо шум и искажения сигнала при передаче и усилении практически отсутствует, потому что 1-битные сигналы имеют цифровую форму.»
А что, n-разрядное слово уже не цифровое?! <-
63 В звуковой технике точность на постоянном токе не важна и часто даже не указывается. Исключением является отличный 20-разрядный ΣΔ ЦАП DAC1220 фирмы TI. <-
64 Такая картина характерна для отфильтрованного сигнала ШИМ, который часто используется для управления скоростью двигателей и яркостью ламп: каждый период частоты Найквиста можно разделить на 64 промежутка, установив несколько первых в единицу, а остальные в ноль. Сигма-дельта - хитрее и лучше. Нули и единицы в её последовательности выплёскиваются за период Найквиста таким образом, чтобы на выходе получился оцифрованный результат высокой точности. <-
65 Краткий анонс для нетерпеливых. Если перейти во временную область, то возможно взаимодействие между выходным фильтром нижних частот, который видит длинный фрагмент битовой последовательности и создающим этот битовый поток модулятором, чей отфильтрованный выход представляет собой точный результат преобразования. Понять ( и просчитать ) это удобнее в частотной области, где модулятор с избыточной передискретизацией уменьшает внутриполосный шум квантования, «выдавливая» его в более высокие ( внеполосные ) частоты. <-
66 Который, как скоро будет ясно, не обязательно делать очень резким: сказывается благотворный эффект передискретизации, см. рис. 13.60 . <-
67 Здесь он для простоты упоминается как 1-битный, хотя на самом деле может быть многоразрядным ( т.е. иметь больше двух уровней ). <-
68 Есть ещё вид преобразований - «аналог-в-аналог», представленный микросхемой HCPL-7800 A фирмы Avago. Это аналоговый опто-изолятор. Его входной модулятор создаёт битовый поток оптически отвязанный от выходного демодулятора. В итоге получается точная и стабильная аналоговая копия: нелинейность 0.004% тип., дрейф усиления 3 ppm/°C тип., полоса 100 kHz и изоляция на уровне киловольт. Ещё одним примером сигма-дельта преобразования аналог-аналог является «Супер Аудио Диск» ( SACD ) - носитель в механическом формате обычного CD-диска, на котором в зашифрованном виде хранится сам промежуточный поток со скоростью 2.8 Mbps . При воспроизведении его нужно пропустить через фильтр нижних частот. <-
69 Битовый поток можно рассматривать и как цифровой ( набор нулей и единиц ), который затем проходит через цифровой фильтр ( если речь идёт об АЦП ), и как аналоговый сигнал, который переключается между двумя фиксированными уровнями напряжения ( если рассматривается ЦАП ). Заметим также, что выражение «только фильтр» не означает, что конструкция этого «только фильтра» проста и тривиальна. Цифровые фильтры вообще не самая простая тема. Она включает проблемы выбора оконной функции, наличие нулей в выходной характеристике и т.д., см. §6.3.7 . <-
70 «Разработка и реализация 18-разрядных звуковых преобразователей аналог-цифра с использованием техники передискретизации». “Design and implementation of an audio 18-bit analog-to-digital converter using oversampling techniques”, J. Audio Eng. Soc. 34, 153-166 ( 1986 ). <-
71 В первом приближении последовательные коэффициенты являются sinc-функцией - реализацией идеального ФНЧ с помощью преобразований Фурье. См. §6.3.7 . <-
72 На практике фильтрация и децимация объединяются в «многоскоростной фильтр-дециматор». <-
73 Вместо более сложной sinc-функции с взвешенным усреднением, которое требуется для построения идеального ФНЧ с вертикальным характером заграждения, см. §6.3.7 . <-
74 Авторы благодарны Болу Адамсу из Analog Devices за конструктивную дискуссию и избавление от тупиков мышления, но если в рассуждения вкрались какие-либо ошибки, то он, конечно, не виноват. <-
75 «You're not wrong, Walter, you're just an asshole.» Big Lebowski <-
76 Принято думать о внешнем шуме как о величине малой по сравнению с основным сигналом, который, собственно, шумом и портится. Здесь же шум квантования ( разница между входным аналоговым сигналом и двухуровневым выходным напряжением \( V_{out}\) ) на самом деле больше [* ! ] самого сигнала. <-
77 Тема хорошо раскрывается Ивом Байзом ( Ewe Beis ) на его сайте 77 Explained nicely by Ewe Beis, on his website at http://www.beis. de/Elektronik/Electronics.html. <-
78 Здесь нужно немного интуиции: на низких частотах ( гораздо ниже \(ω_0\) ) в интеграторе есть большой запас по усилению в замкнутой петле обратной связи, а на выходе - единичный коэффициент. Комбинация входного сумматора и интегратора ничем не отличается от стандартного ОУ со спадом АЧХ вида 1/\( f \) за счёт частотной коррекции. На больших частотах петлевое усиление падает, и именно этим определяется ухудшение характеристик интегратора. <-
79 Снова интуиция: теперь «сигнал» (шум квантования \( V_{qn}\) ) работает как дополнительное возмущение на выходе усилителя с обратной связью и единичным коэффициентом, поэтому он убирается петлевым усилением, которое велико на малых частотах ( величина \(ω_0/ω\) ) , но перестаёт работать выше точки \(ω_0\) . <-
80 Иногда можно встретить утверждение типа: «Сдвинем шум вверх по частоте». В предложенной линейной модели ничего сдвинуть нельзя. Она лишь ослабляет шум на низких частотах и пропускает без ослабления на высоких. Так или иначе, точная модель шума квантования должна учитывать тот факт, что битовый поток с двумя состояниями имеет постоянную амплитуду ( всегда ±1 ), и снижение мощности шума квантования на низких частотах вызывает её рост на высоких. <-
81 Простая каскадная схема может использоваться только для второго порядка и дальше не работает, т.к. начинает накапливаться сдвиг фазы, создающий предпосылки для неустойчивости. Вместо простого каскадирования используется схема взвешенного суммирования. В современных звуковых ΣΔ АЦП стоят модуляторы пятого порядка, что вместе с 64-кратной передискретизацией даёт 20 разрядов эффективного динамического диапазона. <-
82 Следует учитывать, что реальные модуляторы, начиная с третьего порядка, используют модифицированную структуру - взвешенное суммирование выходов интеграторов, для которой формула не вполне корректна. <-

