6.3 (II) Схемы фильтров
==415
6.3.5 Всепропускающие фильтры
Всепропускающие?! Всёпропускающие? [* Да ладно! Вы уже раньше проболтались, что они существуют. Поздно делать удивлённое лицо] . Зачем это нужно? Кому это может понадобиться, если простой кусок провода решит такую задачу, причём, скорее всего, лучше?
Всепропускающие фильтры, известные также в качестве корректоров задержки или корректоров фазы , - электронные устройства с плоской амплитудной характеристикой, но с изменяющимся по частоте сдвигом фазы. Они используются для компенсации сдвигов фаз ( или выравнивания времени задержки ) в пути распространения сигнала.
На рис. 6.41 показана базовая схема. Достаточно понятно, что схема ведёт себя как инвертор на низких частотах ( где на неинвертирующий вход ничего не попадает ) и как повторитель на высоких частотах ( рекомендуется освежить в памяти схему усилителя с переключаемой полярностью из §4.3.1.A ). Выписав пару уравнений, можно убедиться, что схема работает в соответствии с приведёнными графиками. Если поменять местами R и C, то устройство будет работать аналогично, но фаза начнёт отставать ( вместо опережения ) между экстремумами чистого инвертора и чистого повторителя. Величину сдвига можно регулировать, сделав R переменным, но здесь надо учитывать, что малое сопротивление этого резистора снизит входной импеданс схемы на высокой частоте, где реактивное сопротивление C будет близко к нулю.
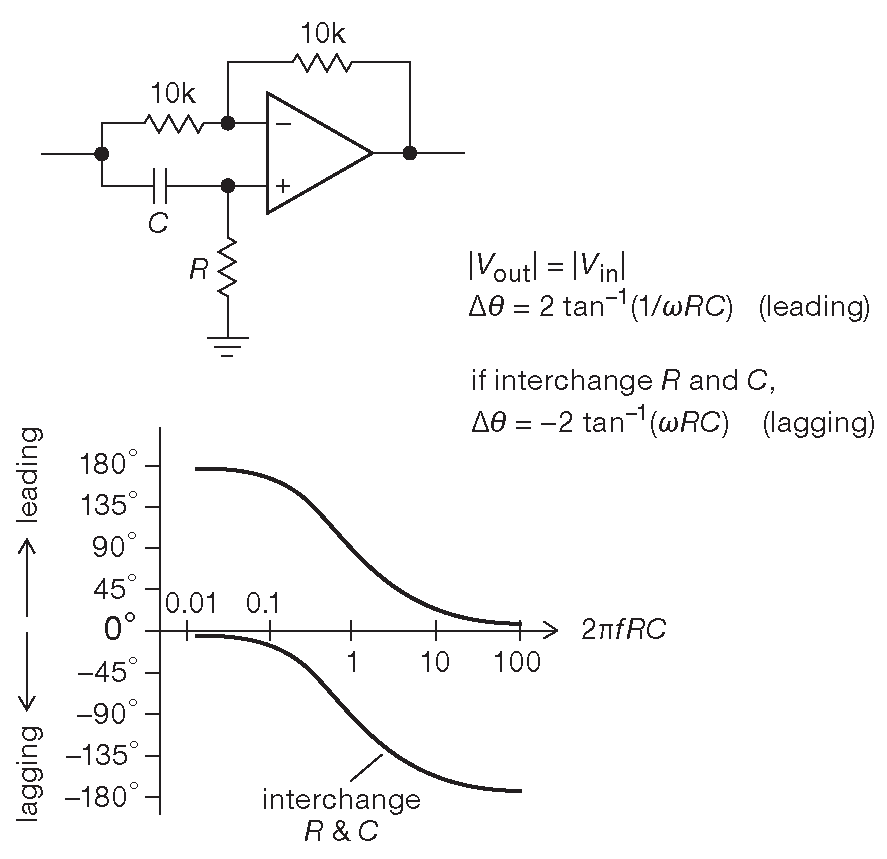
Рис. 6.41 Всепропускающий фильтр, известный как корректор задержки или корректор фазы
Вариант на рис. 6.42 позволяет менять фазу на полные 360° . Недостатком является то, что для сдвига фазы надо менять величину двух компонентов одновременно ( например, пары одинаковых резисторов ). Для таких задач отлично подходят электронные потенциометры ( «EEpot» ), кратко упомянутые в §3.4.3.E .
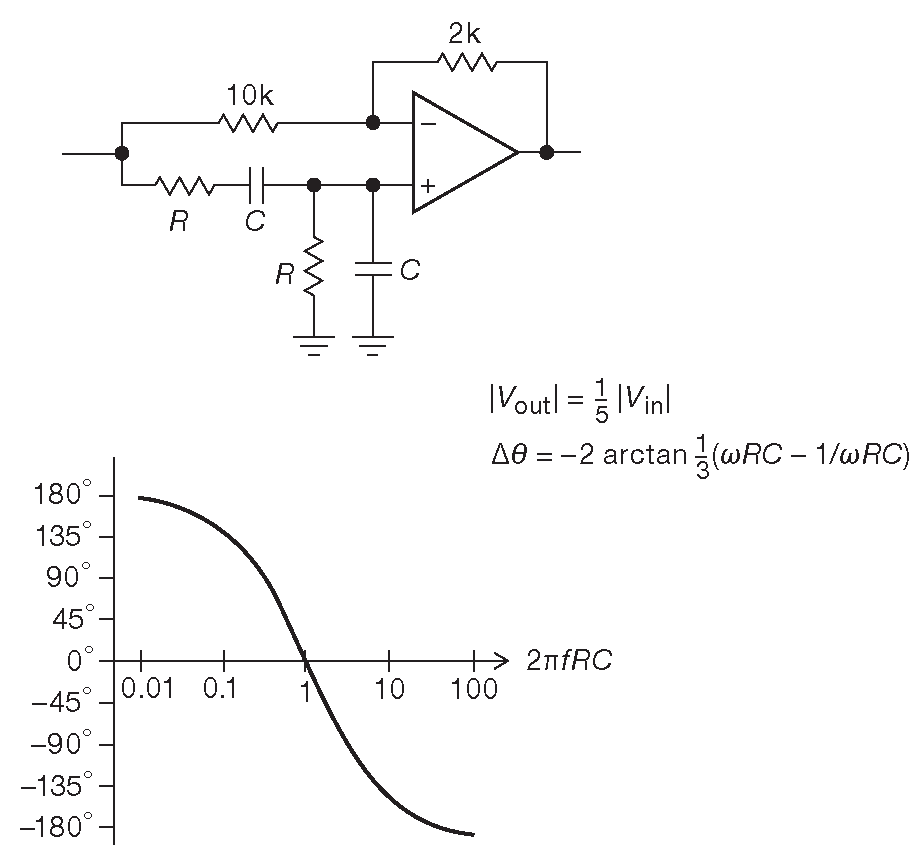
Рис. 6.42 Всепропускающий фильтр с полным диапазоном изменения фазы 360° ( Genin, R., Proc. IEEE, 56, 1746 ( 1968 ))
6.3.6 Фильтры на переключаемом конденсаторе
==416
Одним из недостатков биквадратных фильтров и схем с управляемыми параметрами является необходимость использования хорошо согласованных конденсаторов. Если схема собирается из обычных операционных усилителей, то придётся подобрать парочку стабильных конденсаторов ( танталовые, электролитические и керамические высокой ёмкости не подойдут ), подогнанных с точностью нe хуже 1% , чтобы получить приличные параметры фильтра. Кроме того, придётся сделать много соединений, т.к. схемы используют минимум три операционных усилителя и шесть резисторов для каждой 2-полюсной секции. Или можно купить ИМС активного фильтра, с уже подогнанными интегрированными конденсаторами 1000 pF±0.5% . Производители кремния уже решили указанные проблемы, но хотят за это денег: UAF42 и MAX274 – «универсальные микросхемы активных фильтров» собраны по гибридной технологии с лазерной подгонкой и стоят около $8-16 за штуку. И эти фильтры «непрерывного времени» не предполагают лёгкой подстройки.
6.3.6.A Интегратор на переключаемом конденсаторе
Есть ещё один способ реализации интеграторов, которые нужны в фильтрах с управляемыми параметрами или биквадратных конфигурациях. Исходная идея - использовать МОП ключ с внешним прямоугольным тактовым сигналом достаточно высокой частоты ( обычно требуется в 100 раз большая, чем интересующий аналоговый сигнал), как показано на рис. 6.43 . Симпатичный маленький треугольник с двумя выводами - цифровой инвертор, который обращает фазу на 180° , чтобы два МОП ключа замыкались в разных полупериодах прямоугольного сигнала.
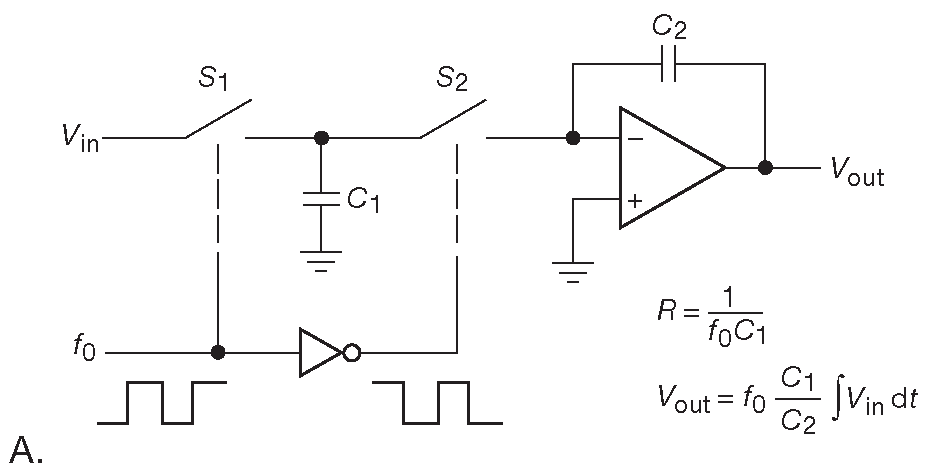
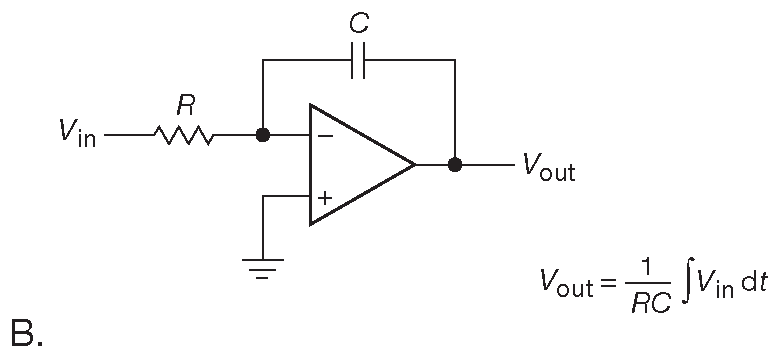
Рис. 6.43 (A) Интегратор на переключаемом конденсаторе. (B) Обычный интегратор
Анализ схемы прост. Когда ключ \( S_1\) замкнут, \( C_1 \) заряжается до \( V_{in}\) , т.е. накапливает заряд \( V_{in}C_1\) . В следующем полупериоде \( C_1 \) разряжается в виртуальную землю, передавая свой заряд на \( C_2\) . Таким образом, напряжение на \( C_2\) меняется на величину \(Δ V=Δ Q/C_2=V_{in}C_1/C_2\) . Отметим, что изменение выходного напряжения в каждом цикле прямоугольного тактового сигнала пропорционально \( V_{in}\) ( предполагается, что последнее меняется за указанное время незначительно [* ибо соотношение частот изначально выбрано 1:100 ] ). Легко показать, что схема подчиняется приведённым соотношениям, т.е. ведёт себя как интегратор.
Упражнение 6.6
Выведите уравнения на рис. 6.43 .
Упражнение 6.7
Есть ещё один способ разбора работы интегратора на переключаемом конденсаторе. Подсчитайте средний ток, протекающий через ключ \( S_2\) в виртуальную землю. Результат должен быть пропорционален \( V_{in}\) . Это означает, что цепь из \( S_1\) , \( C_1 \) и \( S_2\) действует подобно резистору, формируя классический интегратор. Чему равно эквивалентное сопротивление такой цепи в терминах \( f_0\) и \( C_1?\) Учтите, что для приведения к уравнению на рисунке \( V_{out}=f_0( C_1/C_2 )\int V_{in}dt\) .
6.3.6.B Преимущества фильтров на переключаемом конденсаторе
В использовании интеграторов на переключаемом конденсаторе вместо обычных есть два плюса. Во-первых, как уже отмечалось ранее, их проще и дешевле делать в интегральном исполнении, т.к. коэффициент передачи интегратора зависит только от отношения двух емкостей, а не от их абсолютного значения [* \( C_1/C_2\) , а в интеграторе непрерывного времени 1/( \(RC\) )] . В общем случае в кремнии легко создавать согласованные пары, но очень сложно получать точные и стабильные абсолютные величины, что для резисторов, что для конденсаторов. В результате фильтры на переключаемом конденсаторе недороги: ИМС универсального фильтра MF10 фирмы TI имеет два фильтра в одном корпусе и стоит $3.50 ( а одинокий UAF42, построенный по обычной схеме - $16 ).
==417
Во-вторых, фильтры на переключаемом конденсаторе способны менять свои параметры, например, центральную частоту в полосовых фильтрах или точку «-3dB» в ФНЧ, вслед за изменением тактовой частоты 36 . Это возможно, потому что характеристическая частота биквадратной схемы или фильтра с управляемыми параметрами пропорциональна, точнее, зависит исключительно от усиления интегратора.
6.3.6.C Конфигурации фильтров на переключаемом конденсаторе
Микросхемы фильтров на переключаемом конденсаторе выпускают как с жёстко заданной, так и со свободной «универсальной» конфигурацией. В первом случае в корпусе уже собраны все компоненты, нужные для построения ФНЧ требуемого типа ( Баттерворта, Бесселя, Кауэра, т.е. эллиптический ). А в универсальной версии промежуточные сигналы выведены наружу и позволяют собрать любой желаемый фильтр. За универсальность приходится платить большими размерами корпуса и необходимостью подбора внешних резисторов. Например, LTC выпускает законченный эллиптический фильтр 8-го порядка LTC1069-6. Он упакован в 8-ногий корпус и стоит около $9. Их же счетверённый 2-полюсный универсальный фильтр выпускается в 24-ногом корпусе, стоит порядка $15 и требует 12 внешних резисторов для создания чего-либо сравнимого с LTC1069-6 по параметрам. Рис. 6.44 показывает, сколь просто использовать специализированный вариант. Читатель может заглянуть в §7.1.5.A , чтобы ознакомиться с элегантным и простым генератором синуса, который использует следящий фильтр на переключаемом конденсаторе и один источник прямоугольного тактового сигнала с частотой в 128 раз большей, чем выходной синусоидальный сигнал ( рис. 7.18 , 7.19 ).
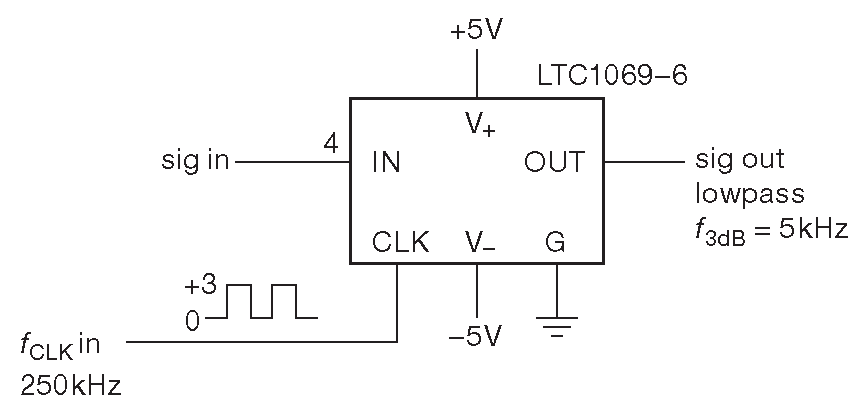
Рис. 6.44 Фильтр с заданной производителем функциональностью не требует внешних компонентов. Эллиптический фильтр 8-го порядка имеет неравномерность 0.1 dB в полосе пропускания и подавление более 40 dB на частоте 1.3×\( f_{3dB} \)
И специализированные и универсальные фильтры используют в качестве базового строительного элемента 2-полюсный фильтр с управляемыми параметрами, в котором классический интегратор непрерывного времени на ОУ заменён схемой с переключаемым конденсатором ( рис. 6.45 ). В универсальном фильтре располагаются четыре таких секции, которые можно каскадировать для увеличения порядка ( каждая секция при этом отвечает за свой элемент многочлена, реализующего функцию фильтра ), либо использовать по отдельности для увеличения числа каналов ( но параметры их будут определяться общим тактированием ). Справочные данные производителей микросхем и предлагаемые ими программы делают разработку фильтров из описанных «заготовок» совершенно несложным делом 37 . Для фильтров с заданной функциональностью считать вообще ничего не надо, достаточно просто включить его в схему.
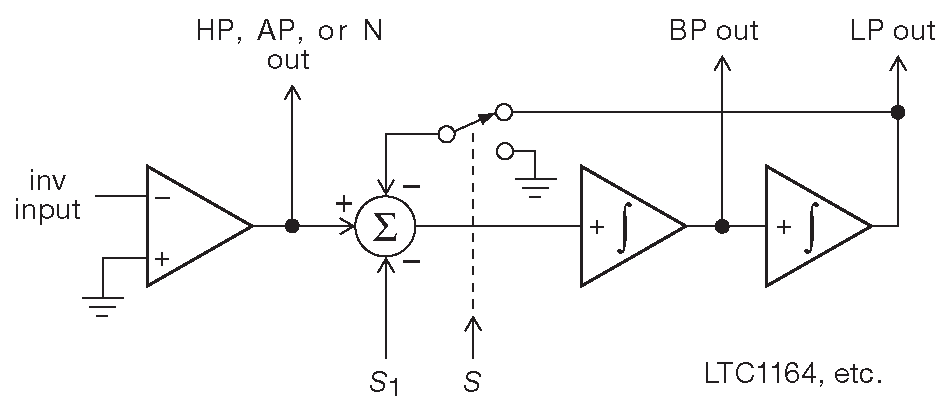
Рис. 6.45 Один строительный блок 2-го порядка «универсального» фильтра на переключаемом конденсаторе. На таком элементе можно собрать фильтр нижних частот, верхних частот, полосовой, заграждающий и всепропускающий. Функция выбирается внешними соединениями. Конденсаторы уже есть внутри, от пользователя требуются только резисторы
6.3.6.D Недостатки фильтров на переключаемом конденсаторе
Теперь о грустном. Фильтры на переключаемом конденсаторе присущи три неприятных свойства, обязанные своим появлением постоянно тикающему тактовому сигналу. Во-первых, имеется проникание тактовой частоты: появление некоторого выходного сигнала ( обычно порядка 10...25 mV ) с частотой тактирования, независимого от входного сигнала. Явление обычно проблем не доставляет, т.к. частота эта сильно отстоит от интересующей аналоговой полосы, и простая RC цепочка поможет с ней справиться.
==418
Во-вторых, возникает и более тонкая проблема. Если во входном сигнале есть частотные компоненты, располагающиеся неподалёку от тактовой частоты, то они будут «перенесены» вниз в рабочую полосу. Если точнее, то вся энергия входного сигнала, попадающего в частотный промежуток шириной в рабочую полосу по обе стороны от тактовой частоты, появятся без какого-либо ослабления в рабочей полосе. Например, если задействовать MAX7400 ( эллиптический ФНЧ 8-го порядка ) в качестве фильтра со срезом на частоте 1 kHz ( т.е. \( f_{clk}\space \)=100 kHz ), вся энергия входного сигнала в полосе 99...101 kHz появится в полосе 0 Hz...1 kHz . Никакой фильтр на выходе убрать её не сможет! [* Готовый компонент для синхронного детектирования, между прочим] . Т.е. необходимо обеспечить отсутствие спектральных составляющих сигнала на частоте тактирования. Если нет прямых противопоказаний, то подойдёт обычный RC фильтр, потому что тактовая частота сильно отстоит от рабочей полосы. Задача организации входного спектрального фильтра упрощается при использовании микросхем с большим отношением тактовой частоты к рабочей ( т.е. 100:1 , вместо 50:1 или 25:1 ). Несколько очень приятных ИМС с отношением 1000:1 [* только для ФВЧ] выпускает фирма Mixed Signal Integration. например, их серия MSHN 38 . Большая разница частот сглаживает «ступенчатость» выходного сигнала этих фильтров. [* Подробнее тема частотных компонент, спектральных фильтров и переноса сигналов разбирается в Части 13 в §13.5.1 ] .
В-третьих, фильтры на переключаемом конденсаторе снижают общий динамический диапазон сигнала, т.к. из-за неполной компенсации переноса заряда в МОП ключе ( §3.4.2.E ) они повышают «общий уровень шума». Это проявляется в увеличении шумов в полосе пропускания. Типовые заявляемые величины динамического диапазона составляют 80...90 dB . В дополнение к уменьшению диапазона ( относительно фильтров непрерывного времени ) фильтры на переключаемом конденсаторе вносят в сигнал больше искажений, чем того можно ожидать. Особенно хорошо это заметно на сигналах, приближающихся к шинам питания.
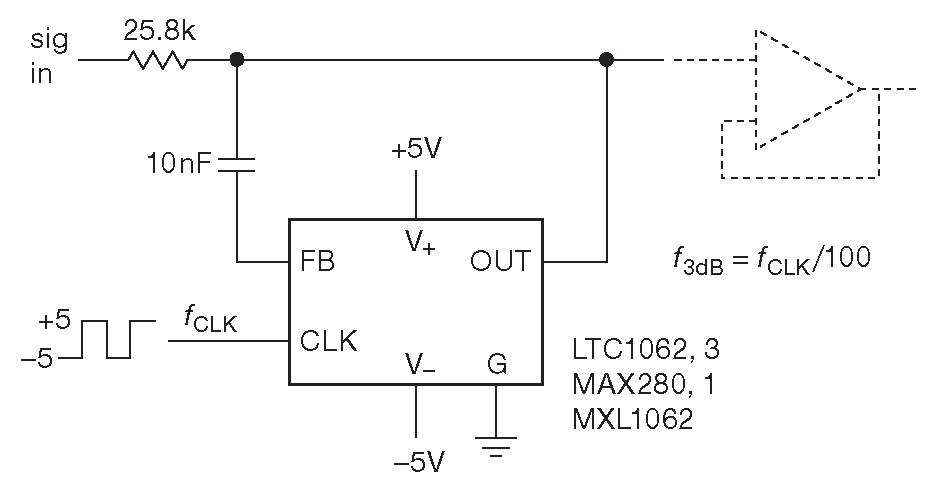
Рис. 6.46 ФНЧ с точным постоянным уровнем LTC1062. Внешний тактовый сигнал должен иметь полный размах питания ( стоит добавить последовательный защитный резистор ). Ещё один вариант включения: поставить конденсатор между выводом «CLK» и землёй, чтобы включить внутренний генератор
Подобно любым линейным схемам, фильтры на переключаемом конденсаторе ( и схемы на ОУ ) подвержены негативному воздействию типовых ошибок усилительных схем, вроде напряжения смещения и низкочастотного шума вида 1/\( f \) . Такое положение создаёт изрядные неудобства, если нужно, скажем, фильтровать какой-нибудь низкоуровневый сигнал так, чтобы не вносить ошибок и смещений в его среднюю постоянную составляющую. В такой ситуации помощь может оказать LTC1062 «ФНЧ без ошибок на постоянном токе» от изобретательной Linear Technology ( или MAX280 с улучшенными параметрами на постоянном токе ). На рис. 6.46 показано, как их использовать. Основная идея: удалить фильтр из пути распространения постоянного тока, позволяя низкочастотным сигналам проходить на выход в пассивном режиме. Фильтр начинает воздействовать на линию только на высоких частотах, где он начинает шунтировать сигнал на землю. В результате получаем нулевую ошибку по постоянному току, а шум самого фильтра попадает в сигнал только в районе частоты среза ( рис. 6.47 ) 39 . Из таких фильтров тоже можно создавать настраиваемый фильтр-пробку, а также каскадировать их, чтобы повышать порядок или заострять переходную характеристику.
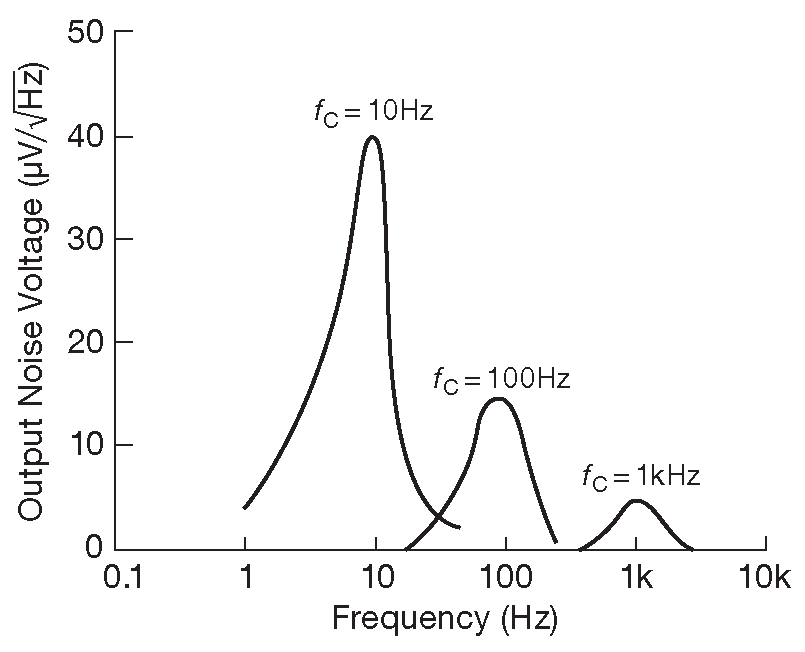
Рис. 6.47 Спектр шума на выходе LTC1062 ( по данным производителя )
Фильтры на переключаемом конденсаторе предлагают многие фирмы, в том числе Linear Technology, TI и Maxim. Их частоту среза ( или центр полосы пропускания ) можно расположить в любом месте от постоянного тока до нескольких десятков килогерц, а отношение характеристической частоты к тактовой составляет 50 или 100 . Большая часть таких микросхем предназначена для работы в качестве ФНЧ, полосовых или фильтров-пробок, но универсальные модели можно включить и в качестве ФВЧ. Отметим, что в последнем варианте пролезание тактовой частоты в сигнальные цепи и эффекты квантования сигнала становятся особенно неприятны, потому что оба явления попадают в полосу пропускания.
6.3.7 Цифровая обработка сигналов
Тема фильтров не может считаться завершённой без упоминания повсеместно используемой техники цифровой обработки сигналов ( DSP ), известной также как техника обработки сигналов дискретного времени . Современные электронные системы, содержащие микропроцессоры, предпочитают цифровые методы фильтрации за их гибкость и эффективность. Цифровая обработка - производство каких-либо действий над сигналами в цифровой форме, когда непрерывный сигнал ( например, речевой ) преобразуется в последовательность цифр, соответствующих последовательным измерениям амплитуды через равные промежутки времени. Под «действиями» может пониматься любая задача, которую можно обнаружить в аналоговом сегменте: фильтрация, сложение, подавление или усиление, нелинейная компрессия, ограничение и т.д. Но, кроме того, сюда попадают и более сложная обработка, опирающаяся на вычислительные возможности процессоров: кодирование, коррекция ошибок, шифрование, спектральный анализ, синтез речи, обработка изображений адаптивная фильтрация, сжатие без потерь и т.п.
==419
Подробный разбор перевода сигналов в цифровую форму будет вестись в Части 13 ( «Аналого-цифровые преобразования» ), а программной обработки в Части 15 ( «Микроконтроллеры» ), где обсуждаются электронные средства преобразования сигналов из аналоговой формы в цифровую и работа с полученными цифрами. Здесь же будет просто представлена цифровая обработка сигналов в приложении к теме фильтрации и краткий обзор возможностей цифровых методов в сравнении с аналоговыми. Речь будет идти только об одномерной фильтрации, т.е. обработке «одномерных» сигналов, например, речевых. Типичным двумерным сигналом является изображение: его значение является функцией двух координат. Одномерные сигналы характеризуются напряжением \( V( t )\) , которое меняется во времени.
6.3.7.A Выборка
Цифровое представление непрерывного сигнала предполагает измерение его амплитуды через равные промежутки ( исключения бывают, но редко ) времени - выборки, с получением набора цифровых значений. Качество перевода сигнала в цифровую форму имеет два параметра: частотную составляющую, определяемую частотой выборки и критерием Найквиста ( см. рис. 13.60 ), и динамическую составляющую, которая объединяет разрядность и шум ( см. §13.5.1 ). Здесь есть о чём поговорить, но на данный момент достаточно знать, что делать выборки надо на частоте, как минимум вдвое превышающей самую высокочастотную компоненту входного сигнала \( f_{samp} \) ≥ 2\( f_{sig}(max) \) , и что для сохранения нужного динамического диапазона оцифровку надо выполнять с n-разрядной точностью с учётом того факта, что динамический диапазон равен (6×n) dB .
Предположим, что аналоговый сигнал оцифрован с помощью аналого-цифрового преобразователя, со спектральным ФНЧ на входе, чтобы гарантировать отсутствие в сигнале гармоник, выходящих за частоту Найквиста \( f_{samp} \)/2 .
6.3.7.B Фильтрация
Последовательность амплитуд ( назовём её \(x_n\) , для n-ного значения ) представляет входной сигнал [* такая последовательность называется «вектором длины < переменная, отвечающая за длину последовательности >»] . Требуется отфильтровать последовательность, скажем, с помощью ФНЧ. Есть два больших класса цифровых фильтров: с конечной импульсной характеристикой - КИХ ( FIR ) и с бесконечной импульсной характеристикой - БИХ ( IIR ). КИХ проще для понимания. Каждое число на выходе такого фильтра является просто взвешенной суммой некоторого числа входных значений ( рис. 6.48 ): \[ y_i=\sum_{k=-∞}^{∞} a_kx_{i-k} \] где \(x_i\) - амплитуды входных сигналов , \(a_k\) - весовые коэффициенты , а \(y_i\) - число на выходе фильтра [*] . В жизни число весовых коэффициентов ограничивают каким-либо значением, поэтому и операцию суммирования проводят только на конечном числе входных значений. Строго говоря, набор коэффициентов - это некое приближение к обратному преобразованию Фурье для желаемой функции фильтра. [**]
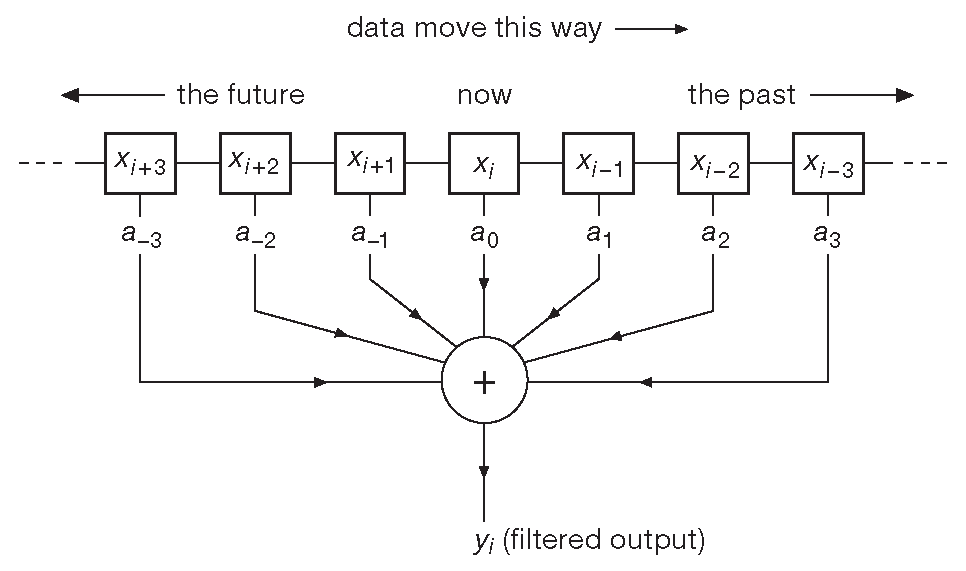
Рис. 6.48 Цифровой фильтр с конечной импульсной характеристикой ( КИХ)
[*]
[* Пояснение картинки
На рисунке описывается момент времени \(i\). Квадратики с пометкой «\(X_{(i+T )}\)» - цифровые значения амплитуды в последовательные моменты времени. Подписи под квадратиками вида «\(a_Z\)» - множители для амплитуды, определяющие «функцию фильтра» ( так же, как номиналы R и C определяют фильтр Чебышева, Бесселя или Баттерворта ). Для получения выходного значения «\(Y_i\)» надо просуммировать ряд произведений ..( \(a_{-3}·X_{i+3}\) ) , ( \(a_{-2}·X_{i+2}\) ) , ... ( \(a_3·X_{i-3}\) )... Данная операция называется «взвешивающее суммирование», \(a_Z\) - «весовым коэффициентом». Число суммируемых произведений определяется числом «точек», т.е. для «##512-точечного» фильтра надо складывать 512 промежуточных произведений. Получение 512 значений «\(a_Z\)» и является задачей расчёта цифрового фильтра. Дальше будет дан простой пример ].
[**]
[* Прямое преобразование Фурье раскладывает сигнал по спектральным составляющим, коих в реальных условиях бесконечно много, на что намекают символы бесконечности в индексах суммы из уравнения. Соответственно, частичная сумма составляющих восстанавливается в сигнал с некоторой погрешностью, см. §A.4* ] .
Отметим интересное и важное свойство такого фильтра: его выход формируют выборки как из «прошлого» [* на рис. 6.48 \(x_{i-1}\) , \(x_{i-2}\) , \(x_{i-3}\)] , так и из «будущего» [* \(x_{i+1}\) , \(x_{i+2}\) , \(x_{i+3}\) , а «настоящее», стало быть, \(x_i\)] . Таким образом, операция нарушает причинно-следственную связь ( эффект должен следовать за причиной его появления ). Это возможно, потому что существует общая задержка между входным и выходным сигналами. [* Ну, иначе говоря, «это невозможно» . [***] ] . Способность «видеть будущее» ( которым не обладает аналоговый фильтр ) позволяет цифровому фильтру реализовывать амплитудные и фазовые характеристики, которые невозможны в аналоговых фильтрах, встречавшихся до настоящего времени.
[***]
[* Для проведения операции суммирования в буфере фильтра уже должны быть отсчёты из так называемого «будущего». Это значит, что заглянуть в будущее можно, только когда оно уже произошло, в строгом соответствии с принципом «Чтоб я таким умным был ДО, как моя Сара ПОСЛЕ». Вместо переменной «Сара» надо подставить требуемую функцию цифрового фильтра.
Ещё раз.
Будущее относительно отсчёта \(x_i\) и соответствующего ему выхода \(y_i\) ( которые нифига не уникальны, что бы они о себе ни воображали ). Но к моменту начала работы с \(x_i\) в очереди на обработку может уже находиться, скажем, \(x_{i+1000}\) отсчёт, т.е. о реальном предвидении речь не идёт. Задержка в цифровом фильтре его имманентное свойство и никаких причинно-следственных законов он не нарушает.
Аналоговый вариант является фильтром непрерывного времени, где нет дополнительной задержки, зато есть время зарядки конденсаторов, изменения тока в индуктивностях и скорости нарастания ОУ, короче, времена сравнимы. Другое дело, что цифровые данные удобнее обрабатывать, и делать это можно, выбирая время, место и способ, а с аналоговой величиной можно работать только «здесь», только «сейчас» и только в рамках, налагаемых схемотехникой. См. примечание в §6.2.6.B ].
БИХ (IIR ) фильтр отличается тем, что его собственное выходное значение со своим весовым коэффициентом используется при суммировании наравне с входными данными, как в КИХ схеме. Поэтому их называют рекурсивными фильтрами. В качестве простейшего примера может выступать выражение \[ y_i = b·y_{i-1} + (1 - b)·x_i, \] каковое является цифровым аналогом RC фильтра непрерывного времени. Для такого случая коэффициент \(b\) должен составлять \(b=e^{[-τ/( RC )]}\) , где \(τ\) - время между выборками. Ситуация, конечно, не идентична работе аналогового фильтра низких частот с аналоговым сигналом из-за прерывистой [* линейчатой, разрывной, дискретной ] природы результатов периодического измерения амплитуды аналогового [* непрерывного ] сигнала.
==420
Оба типа фильтров и КИХ, и БИХ имеют свои «про» и «контра». КИХ выбирают чаще, потому что проще понять, как они работают, их проще реализовать, они стабильны по своей природе ( нет обратной связи ) и их можно сделать линейно фазовыми ( т.е. с постоянной, не зависящей от частоты задержкой ), что чаще всего и происходит. БИХ варианты экономичнее, требуют меньше коэффициентов [* т.е. меньше шагов умножения-суммирования ] , а значит меньше памяти и вычислительного времени. По такой схеме проще реализовывать алгоритмы классических аналоговых фильтров. Наконец, они особенно удобны для задач, требующих высокой избирательности, например, фильтров-пробок. Зато им требуется бОльшая разрядность при вычислениях, чтобы избежать нестабильности и «тонов паузы» [* см §13.9.10 ] и их труднее переводить в программную форму.
6.3.7.C Пример: БИХ фильтр нижних частот
В качестве простого примера предположим, что требуется отфильтровать набор чисел, представляющих сигнал, с помощью ФНЧ с частотой среза \( f_{3dB}=1/( 20t_S ) \) , т.е. аналога простой RC секции с такой же частотой среза. Постоянная времени в данном случае равна промежутку времени, который занимают 20 выборок. Отсюда, A=0.95123 , а выход равен \[ y_i = 0.95123y_{i-1} + 0.04877x_i. \]
Чем больше постоянная времени в сравнении с промежутком между выборками \( t_S\) , тем точнее цифровой фильтр повторяет аналоговый.
Цифровой фильтр можно наложить на уже имеющиеся в памяти данные. В таком случае он превращается в простую вычислительную операцию, проводимую над всеми данными за один раз. [* Как насчёт видения «будущего» в этом случае? А чем данный вариант отличается от работы с АЦП «on-line»? ]
6.3.7.D Пример: КИХ фильтр нижних частот
Идеальный фильтр нижних частот имеет единичный отклик на частоте среза \( f_c\) и нулевой выше неё. Т.е. АЧХ должна быть прямоугольной ( «кирпичная стенка» ). В первом приближении коэффициенты \(a_k\) КИХ фильтра задаёт прямоугольное преобразование Фурье, а именно \(\sin(x)/x\) ( или sinc функция ), в которой масштабирование аргумента зависит от отношения между частотой среза и частотой выборки: \[ a_k∝ \frac{\sin( 2πkf_n )}{2πkf_n} \qquad [6.18] \] где целые k лежат в промежутке от \(-∞\) до \(+∞\) , а \( f_n\) - нормализованная частота среза, определяемая как \( f_n = f_c/f_s\) .
В реальных вычислениях используется конечное число множителей k . Пусть их будет N . Возникает вопрос, какой ограниченный набор коэффициентов фильтра \(a_k\) , где k лежит в промежутке от -N/2 до +N/2 , в наибольшей степени соответствует идеальному фильтру нижних частот? Ответ гораздо сложнее, чем кажется в первый момент. Помимо всего прочего он зависит от того, что следует понимать под термином «в наибольшей степени».
Если просто отбросить все коэффициенты, выходящие за длину суммируемого массива выборок, итоговая характеристика фильтра будет иметь большие выбросы на АЧХ в полосе заграждения, т.е. плохое подавление на некоторых частотах. Это точный аналог проблемы «утечки спектра» в цифровых анализаторах спектра или дифракции боковых лепестков в оптике. И способ борьбы тот же: нужно плавно уменьшать коэффициенты \(a_k\) , масштабируя их с помощью «оконной функции». Сама функция должна плавно сходить на нет с двух сторон ( в спектральном анализе умножают входные цифровые значения амплитуды сигнала на подобную оконную функцию, а в оптике «усекают» апертуру маской, чья плотность увеличивается по направлению к краям ). В результате сильно снижаются пульсации в полосе заграждения, но увеличивается «плавность» перехода от пропускания к заграждению ( в спектральном анализе приём сильно уменьшает утечку спектра в соседние группы частот, но увеличивает ширину групп; в оптике боковые лепестки уменьшаются, но снижается и разрешение в форме более широкой «функции размывания точек» ). Наиболее известные оконные функции имеют имена Хэмминга, Хэннинга и Блэкмен-Харриса. Не существует «самого лучшего» окна: всегда приходится выбирать между скоростью перехода к полосе заграждения и уровнем заграждения в ней. Но по большей части не имеет никакого значения, какая именно функция из числа стандартных выбрана 40 .
Вторым аспектом является выбор такой частоты среза \( f_n\) , чтобы для неё хотя бы часть коэффициентов полинома становилась равной нулю. За счёт нулевого масштабного множителя можно сократить число умножений и сложений для соответствующих членов суммы. Например, такая ситуация возникает, если \( f_n\)=0.25 ( частота выборок в четыре раза выше частоты среза ). Для такого случая коэффициенты из уравнения [6.18] станут \[ a_k∝ \frac{\sin(πk/2 )}{πk/2} \qquad [6.19] \] т.е. все коэффициенты при чётных k , кроме \(a_0\) , обнуляются [* \(\sin(π) = 0\) , и, кстати, в русской математической школе нуль к чётным числам не относится ] . Ещё один бонус можно получить, выбирая длину фильтра N кратной 4 . Такой вариант исключает краевые члены ( для k=±N/2 ), потому что k в этом случае гарантированно чётное.
==421
Т.к. максимальная частота среза, допускаемая теоремой Найквиста равна половине частоты выборок ( \( f_n\)=0.5 ), фильтр со срезом \( f_n\)=0.25 называется «half-band». Рис. 6.49 и 6.50 показывают результат фильтрации при N=8, 16, 32 и 64 , где коэффициенты считаются по уравнению [6.19] для оконной функции Хэмминга. Последняя проявляется в виде косинуса и выглядит приблизительно так: \[ w(k )=0.54 + 0.46\cos( 2πk/N ). \qquad [6.20] \]
Последним шагом является нормализация коэффициентов ( масштабирование в единой пропорции ) так, чтобы их сумма была равна 1 , т.е. усилению фильтра на постоянном токе. Таким образом, порядок таков:
- выбрать N ( предпочтительны значения, кратные 4 );
- для каждого положительного нечётного k вплоть до k=N/2 рассчитать sinc-функцию по уравнению [6.19] и
- умножить результат на коэффициент Хэмминга из уравнения [6.20] , чтобы получить \(a_k\) ( пока не нормализованные ).
Стоит отметить, что коэффициенты симметричны ( \(a_{+k}=a_{-k}\) ) , а член \(a_0\) всегда равен единице, т.к. и \( sinc(0) \) , и \(w(0) \) имеют единичное значение.
- На последнем шаге надо нормализовать все коэффициенты, разделив каждый на их общую сумму.
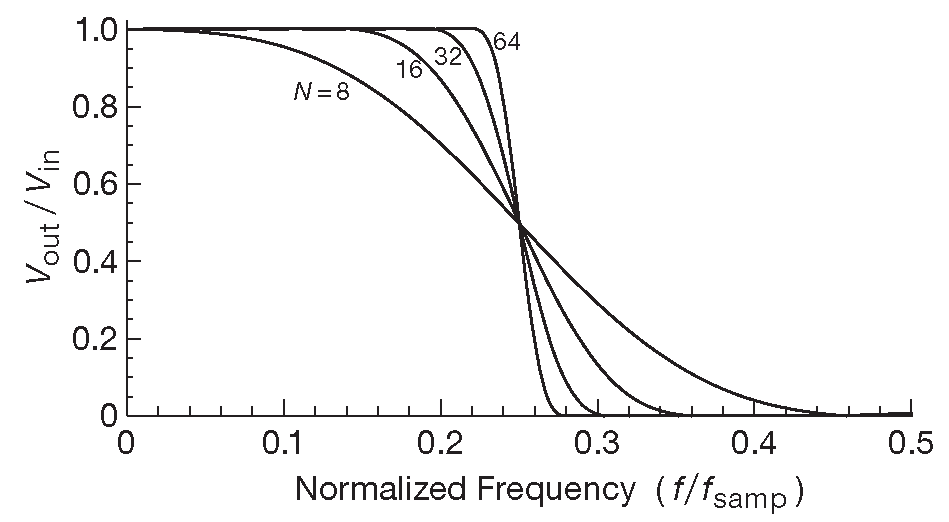
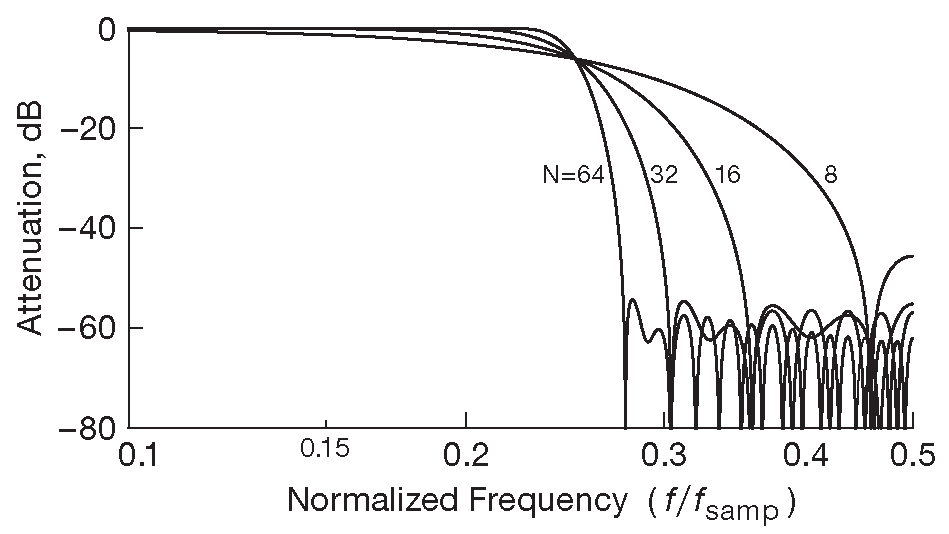
Рис. 6.49 АЧХ КИХ-фильтра половинной полосы в линейных координатах. Фильтр порядка N требует (N/2)+1 коэффициент
Рис. 6.50 АЧХ фильтра с рис. 6.49 в логарифмических координатах лучше показывает процессы в полосе заграждения
Т.к. все чётные коэффициенты равны нулю, то, хотя длина данных остаётся равной N значений, число коэффициентов уполовинивается ( почти, из-за \(a_0\) ) , т.е. для случаев на рис. 6.49 , 6.50 равно 5=(8/2)+1, 9=(16/2)+1, 17 и 33 . Если читатель захочет проверить расчёты, то для случая N=8 он должен получить: \[ \begin{align} a_0 &= &+0.497374 \\ a_1 = a_{-1} &= &+0.273977 \\ a_2 = a_{-2} &= &0 \\ a_3 = a_{-3} &= &-0.022664 \\ a_4 = a_{-4} &= &0 \end{align} \]
Дополнительные мысли: проблемы выбора оконной функции
В примере на рис. 6.49 и 6.50 использовалась оконная функция Хэмминга, частично по лености авторов ( меньше расчётов ), частично, оттого что это неплохой выбор с точки зрения уровня подавления ( ∼60 dB ). Но, как уже отмечалось ранее, можно получить более высокие параметры в полосе заграждения ценой несколько более пологого перехода к ней. Данный тезис отлично иллюстрирует рис. 6.51 , где даны результаты расчётов для КИХ ФНЧ половинной полосы с N=32 для трёх оконных функций. Коэффициенты для окна Блэкмена-Харриса получаются при сложении двух или трёх синусоидальных составляющих [* \(a_0\) не учитывается ] с весовыми коэффициентами, выбранными для минимизации уровня боковых лепестков. Выглядит это так: \[ w(k ) = a_0 + a_1\cos( 2πk/N )+a_2\cos(4πk/N )+a_3\cos( 6πk/N ), \] где коэффициенты \(a_i\) для 3-элементной суммы равны \([a_0\) , \(a_1\) , \(a_2\) , \(a_3]\)=[ 0.42323, 0.49755, 0.07922, 0 ], а для 4-элементной - [ 0.35875, 0.48829, 0.14128, 0.01168 ]. Такие оконные функции позволяют получить впечатляющее подавление ( ∼85 и ∼105 dB соответственно, а у окна Хэмминга ∼55 dB ), но имеют более мягкий переход к заграждению. Стоит добавить, что речь идёт о модельных значениях, к коим на практике можно только приблизиться, и только если умножение и суммирование будут вестись с требуемой точностью, а АЦП имеет высокую линейность.
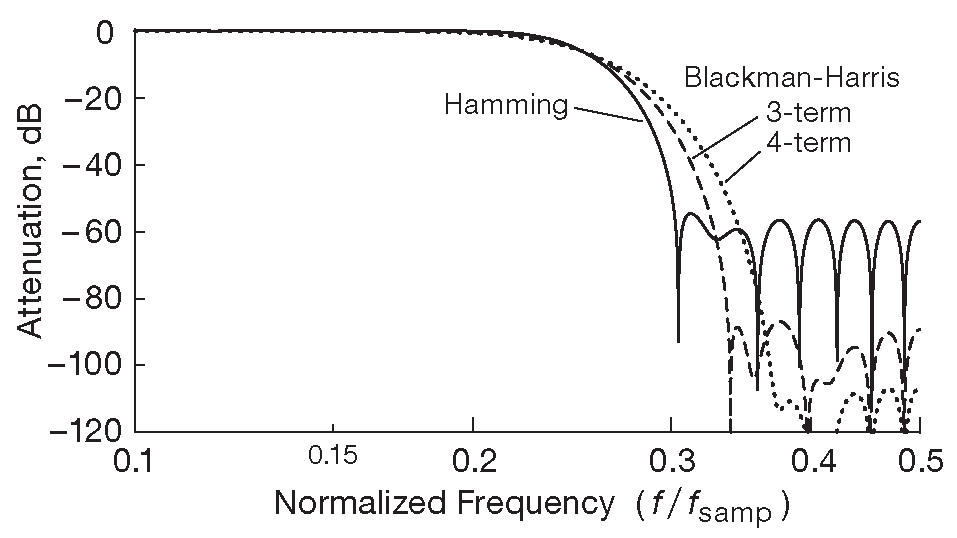
Рис. 6.51 КИХ ФНЧ половинной полосы порядка N=32 , рассчитанный с тремя оконными функциями. Обратите внимание на изменение вертикального масштаба по сравнению с рис. 6.49 и 6.50
==422
6.3.7.E Реализация
Цифровой фильтр можно собрать на дискретных элементах - сдвиговых регистрах, умножителях, аккумуляторах и всех прочих железках, которые описываются в Части 10 и 11 [* а также по смешанной технологии: цифровой источник + аналоговый умножитель и сумматор, см. §13.14.8 и рис. 13.119 , на котором сухая математическая модель с рис. 6.48 явлена «во плоти» ] . Но сейчас такая попытка будет выглядеть слишком эксцентричной. Современные вычислительные средства ( процессоры и микроконтроллеры ) позволяют решить такую задачу с гораздо большим удобством. Более того, существует целый класс специализированных процессоров, оптимизированных для операций умножения и сложения с накоплением, которые потребуются при расчётах, и эффективной обработки больших входных и выходных потоков данных. В качестве примера можно назвать серию TMS320 фирмы TI. На момент написания книги она включала кристаллы TMS320C64xx, которые способны выполнять 1k-точечное быстрое преобразование Фурье ( БПФ FFT ) за время порядка 1 μs (!), проводить обработку 10'000-элементного массива данных с помощью 32-коэффициентного КИХ фильтра за 108 μs . На другом конце спектра вычислительных средств находятся QF1D512 фирмы Quickfilter Technology. Это недорогая отдельная микросхема - 512-точечный КИХ-фильтр для чисел с разрядностью от 12 до 24 бит, следующих со звуковой частотой, и 32-разрядными программируемыми коэффициентами. Стоит меньше $2 в небольших количествах, поставляется вместе с бесплатным программным обеспечением и имеет массу отладочных плат.
6.3.8 Дополнительные замечания по фильтрам
6.3.8.A Линейность
В некоторых задачах фильтрации требуется сохранять высокую линейность передачи амплитуды, притом даже, что фильтр ослабляет разные частоты по-разному. Такое свойство требуется в частности в звуковоспроизведении. В таких местах следует использовать операционные усилители с малыми искажениями ( которые специально отмечены в справочных данных ) с подходящей полосой, скоростью нарастания и усилением. В качестве возможных кандидатов можно назвать LT1115, OPA627 и AD8599, см. табл. 5.4 на стр. 310 и обсуждение проблем разработки схем на быстрых ОУ в §5.8 . Дополнительные материалы есть в Части X4 . Не так очевидно, но столь же необходимо, использовать пассивные компоненты с хорошей линейностью. Первая неприятность, поджидающая на этом пути - керамика высокой ёмкости имеет умопомрачительную зависимость ёмкости от приложенного напряжения. Следом идут электролитические конденсаторы с чётко выраженным эффектом памяти, вызванным диэлектрической абсорбцией ( обсуждение в Части X1 [* ##§X1.3 ] ). В фильтрах надо использовать плёночные (желательно полипропиленовые ) конденсаторы или керамику NPO/C0G.
В LC цепях надо использовать катушки, намотанные на магнитном материале с хорошей линейностью. Это большая проблема для любых магнитных материалов, отсутствующая только в катушках в воздушным «сердечником». Последние имеют разумные размеры при номиналах до 1 mH или около того.
6.3.8.B Программы для расчёта фильтров
Когда-то разработка фильтров была сложной проектной задачей. Те времена ушли. Существует достаточно специализированных удобных в работе программ. Для фильтров непрерывного времени надо задать требования по пропусканию и заграждению ( частоту среза, пульсации, подавление и т.д. ) и программа выдаст число секций в зависимости от конфигурации ( Саллена-Ки, биквадратная и т.д. ) и типа ( «Бессель», «Чебышев»,.. ), схему и графики АЧХ/ФЧХ и времен задержки от частоты. Такие же программы есть и для фильтров на переключаемом конденсаторе. Ниже даётся список полезных, по мнению авторов, ресурсов. Большая их часть свободная, но есть и коммерческие.
-
LC filters:
- http://www-users.cs.york.ac.uk/~fisher/lcfilter/
- MMICAD ( Optotek ) -
Analog active filters
- EilterPro ( TI )
- EilterCAD ( LTC )
- ADI Analog Filter Wizard
- http://www.beis.de/Elektronik/Eilter/Filter.html
-
Digital filters:
- http://www-users.cs.york.ac.uk/~fisher/mkfilter/ -
All types
- Filter Solutions, Filter Light, and Filter Free (http://www.nuhertz.com/filter/)
==422
36 Большинство фильтров на переключаемом конденсаторе имеют частоту среза, равную 1/50 или 1/100 от тактовой. <-
37 В программе надо задать характеристическую частоту, подавление в полосе заграждения, пульсации в полосе пропускания и усиление. Программа сообщает требуемый порядок фильтра и номиналы резисторов. На выходе - графики усиления, фазы и задержки от частоты ( единицы осей по выбору ) и табличные значения, если требуются. <-
38 См. разбор работы MSHN5 в статье Джона Амброза ( John Ambrose ) “Notch filter autotunes for audio applications”, EDN Design Ideas, June 24, 2010. <-
39 Такой же трюк используется в многокаскадных FDNR фильтрах на GIC. <-
40 Чтобы узнать об оконных функциях больше, чем вам бы того хотелось, см. E. J. Harris, Proc. IEEE, 66, 51-83 ( 1978 ). <-

