5.8 Выходные ошибки усилителя
==307
В Части _4 ( §4.4.2 ) говорилось о серьёзных ограничениях выходного каскада операционных усилителей. Конечная скорость нарастания, переходные искажения ( §2.4.1.A ) и выходное сопротивление в цепи без обратной связи могут порождать разнообразные трудности и, если их не учитывать, вызывать в прецизионных схемах ошибки, превосходящие самые мрачные ожидания.
5.8.1 Скорость нарастания: общие соображения
Как указывалось в §4.4.1.K , операционный усилитель может изменять напряжение на своём выходе с какой-то максимальной скоростью. Этот эффект обусловлен внутренней цепью частотной коррекции ОУ и его механизм будет подробно рассмотрен чуть позднее. Первым следствием конечной скорости нарастания является ограничение размаха выходного сигнала на высоких частотах величиной \( Vpp=S/(πf) \) ( §4.4.2.B ). В графическом виде проблема представлена на рис. 5.11 .
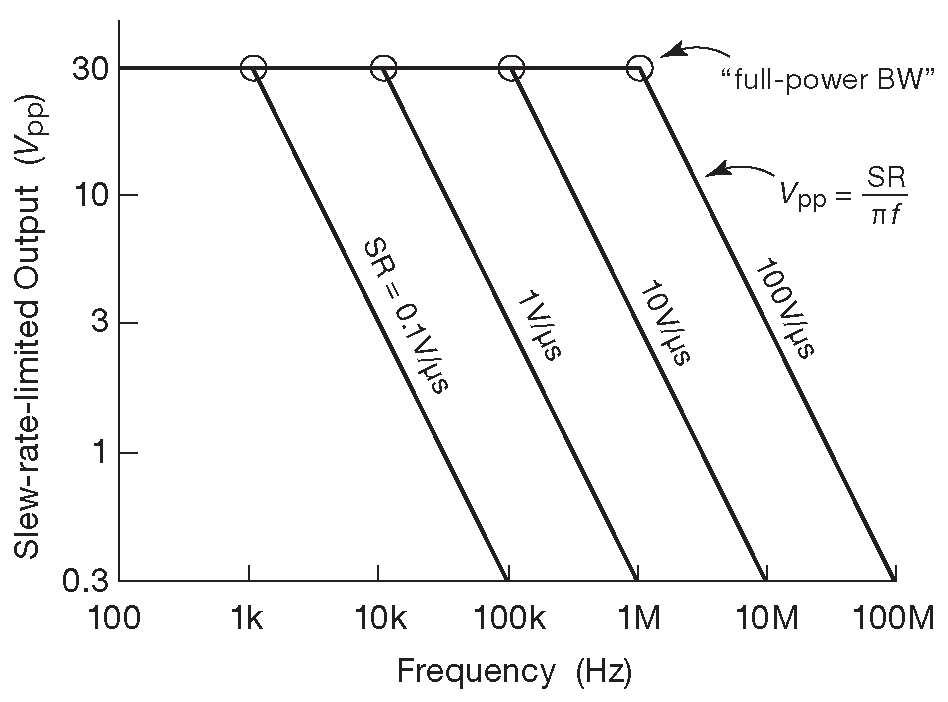
Рис.5.11 Зависимость максимального размаха выходного сигнала от частоты
Второе следствие проще объяснить с помощью рис. 5.12 - графика зависимости скорости нарастания от величины входного сигнала. Основная мысль заключается в том, что если от устройства требуется большая скорость нарастания, то оно должно работать с большим сигналом ( напряжением ошибки ) на входе. Это может быть опасно для схемы, претендующей на высокую точность: чем больше сигнал рассогласования в цепи обратной связи, тем быстрее меняется сигнал на выходе, и тем сильнее искажается его форма. См. данные измерений уровня искажения на рис. 5.19 на стр. 310 . Например, у LT1013 скорость нарастания S=0.8 V/μs .
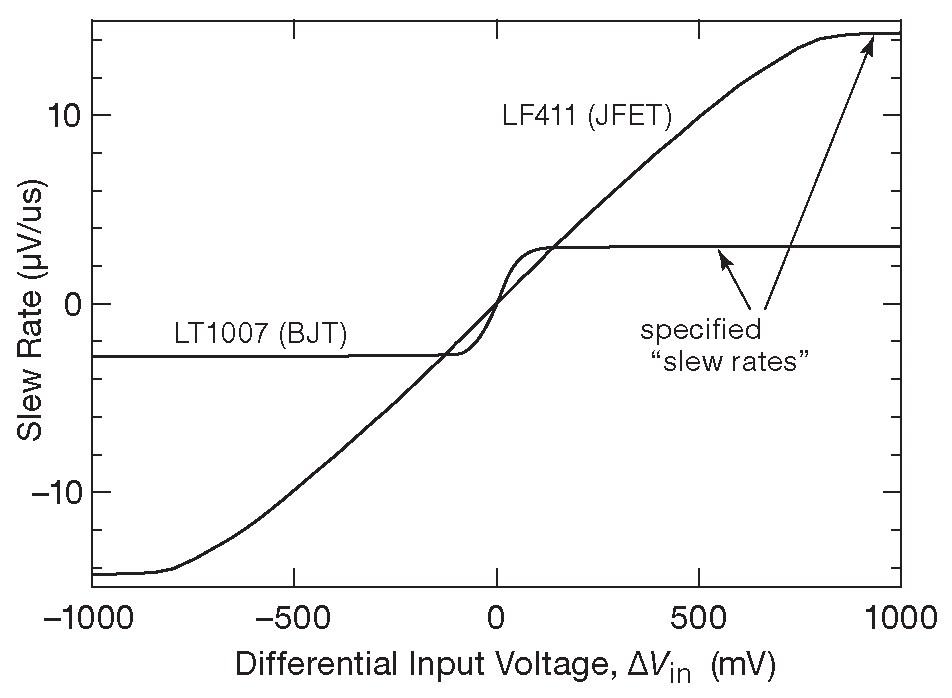
Рис.5.12 Как можно видеть на этом графике, для получения полной скорости нарастания требуется большой дифференциальный сигнал на входе. В БТ усилителях для достижения максимальной скорости нужен сигнал величиной ∼60 mV , для ПТ- и КМОП усилителей амплитуда приближается к вольту
Пора заглянуть внутрь операционного усилителя, чтобы разобраться в причине ограничения скорости нарастания ( более подробное рассмотрение вопроса см. в ##§X4.9 ). Подавляющая часть операционных усилителей сделана по «Схеме Видлара», приведённой на рис. 5.13 . Дифференциальный каскад 18 , нагруженный токовым зеркалом, работает на каскад с большим усилением по напряжению с корректирующим конденсатором между входом и выходом. На выходе стоит буфер с единичным усилением. Величина корректирующего конденсатора \( C \) выбирается так, чтобы снизить усиление в цепи без обратной связи до единицы перед тем, как сдвиг фазы в следующих каскадах достигнет значимой величины. То есть \( C \) выбирается, чтобы \( f_T \) - частота единичного усиления - располагалась вблизи частоты спада следующего каскада, как описано в §4.9 . Входной каскад имеет очень большой выходной импеданс и для последующей схемы выглядит как источник тока.
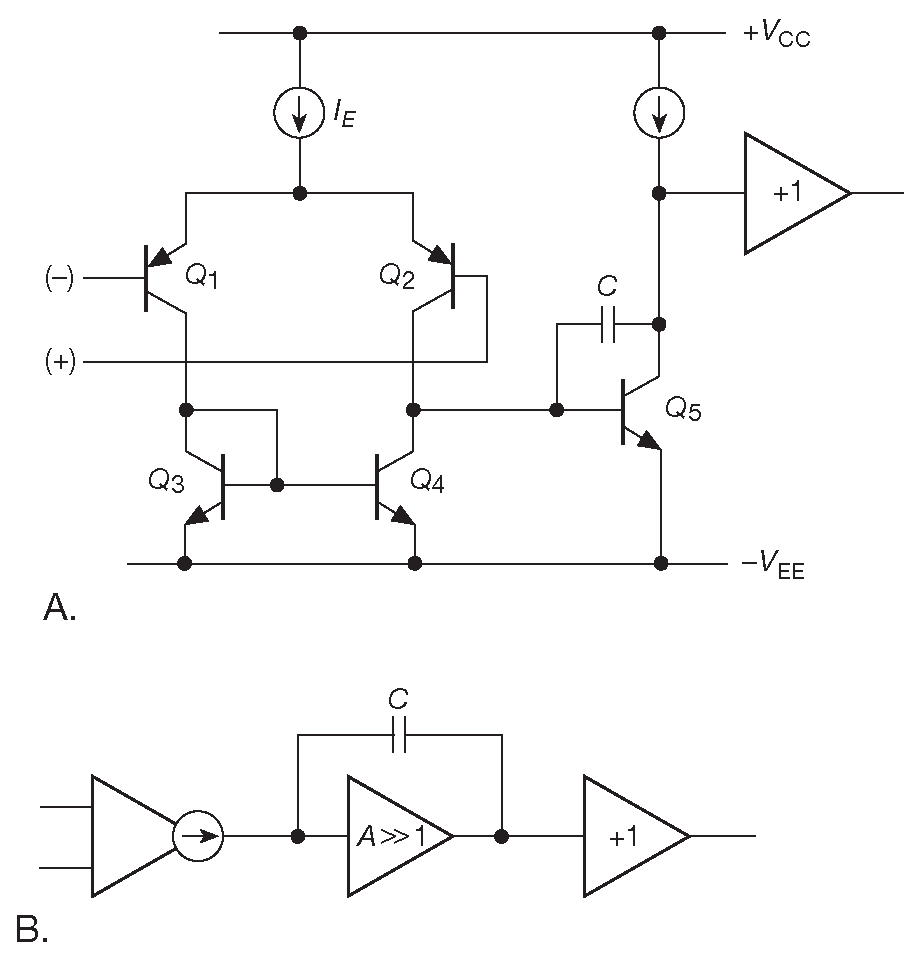
Рис.5.13 Типичная цепь внутренней частотной коррекции
==308
Скорость нарастания ограничивается когда входной сигнал переводит один из транзисторов дифференциального каскада в состояние, близкое к состоянию отсечки. загружая второй каскада полным током дифференциальной пары \(I_E\) . Для биполярного входного каскада это происходит, когда входной сигнал приближается к 60 mV , а соотношение токов в транзисторах подходит к 10:1 . В этот момент \(Q_5\) меняет потенциал на коллекторе с максимально возможной скоростью, перезаряжая \( C \) полным током \(I_E\) . Транзистор \(Q_5\) и \( C \) образуют интегратор, ограничивающий скорость изменения выходного напряжения. Зная принцип работы биполярного транзистора ( ##§X4.9 ), несложно вывести аналитическое выражение для скорости нарастания. Подводя итог, классический входной каскад на БТ с рис. 5.13 имеет скорость нарастания S≈0.3 \( f_T \) .
Чтобы получить бОльшую скорость нарастания, надо взять ОУ с большей частотой \( f_T \) . Если усиление в цепи с обратной связью больше единицы, можно использовать недокорректированный усилитель ( с большей частотой \( f_T \) ) . Существует предел S≈0.3 \( f_T \) , который предполагает, что скорректированный для единичного усиления ОУ с биполярным входным дифференциальным каскадом работает с максимальным усилением, например, \(R_E\)=0 . Есть и способы преодоления указанного предела ( они разбираются в ##§X4.9 ). Вот они.
- Использовать ОУ с уменьшенной крутизной входного каскада ( работает для ОУ как на полевых, так и на биполярных транзисторах с обратной связью в эмиттере ).
- Использовать усилитель с другой конфигурацией входного каскада, специально спроектированной для повышения скорости нарастания. В качестве примера можно упомянуть схемы «с подавлением перекрёстной проводимости», которые используются в семействе TLE2142, и усилитель по схеме ##Бутлера ( используется в OP275 и OP285 ), см. ##§X4.9.
- Использовать усилитель с обратной связью по току или вариант CFB с буфером на инвертирующем входе, который имитирует обычный ОУ с обратной связью по напряжению .
Это рабочие приёмы. Если обозначить степень улучшения за «m» ( т.е. S=0.3×m×\( f_T \) ) , то у LF411 ( входной каскад на ПТ рис. 5.12 ) m=12 , у классического биполярного LT1007 m=1 , у TLE2141 ( входной каскад на БТ с перекрёстными связями ) m=25 , у OP275/285 ( входной каскад Бутлера ) m=8 , LT1210 ( CFB ) с рекомендуемым резистором обратной связи m=55 , а у LT1351 ( CFB, в шкуре VFB ) m=220 .
Подробное рассмотрение скорости нарастания можно найти в Части X4 ( ##§X4.9 ).
5.8.2 Рабочая полоса и время установления
==309
Скорость нарастания показывает, как быстро может меняться напряжение на входе. В операционном усилителе этот параметр предполагает, что на входе присутствует большой дифференциальный сигнал ( 60 mV и более ), хотя это может увеличивать искажения на выходе. Обоснованием такого положения служит тот факт, что для усилителя, выходной потенциал которого не соответствует ожидаемому, обратная связь начинает активно менять сигнал на входе [* изменяя выходной сигнал, т.к. это единственный способ изменить потенциал на входе, см. §4.1.3 (I) ] ( предполагается, что усиления в петле обратной связи достаточно для этого [* т.е. выходной сигнал, прошедший обратно на вход через ветвь обратной связи и масштабированный с коэффициентом \( G_{cl}\) ( «петлевое усиление» ) достаточен для компенсации входного изменения ). В точных быстродействующих схемах столь же важным вопросом является время, потребное для изменения выходного потенциала в соответствии со входным воздействием. Этот параметр называется «время установления» ( время, требуемое для достижения заданного значения с заданной точностью при условии невыхода в последствии из данного допуска, см. рис. 5.14 ) и редко приводится для ОУ, но всегда указывается для АЦП и прочих подобных устройств, в которых точность - то ради чего всё затевается.
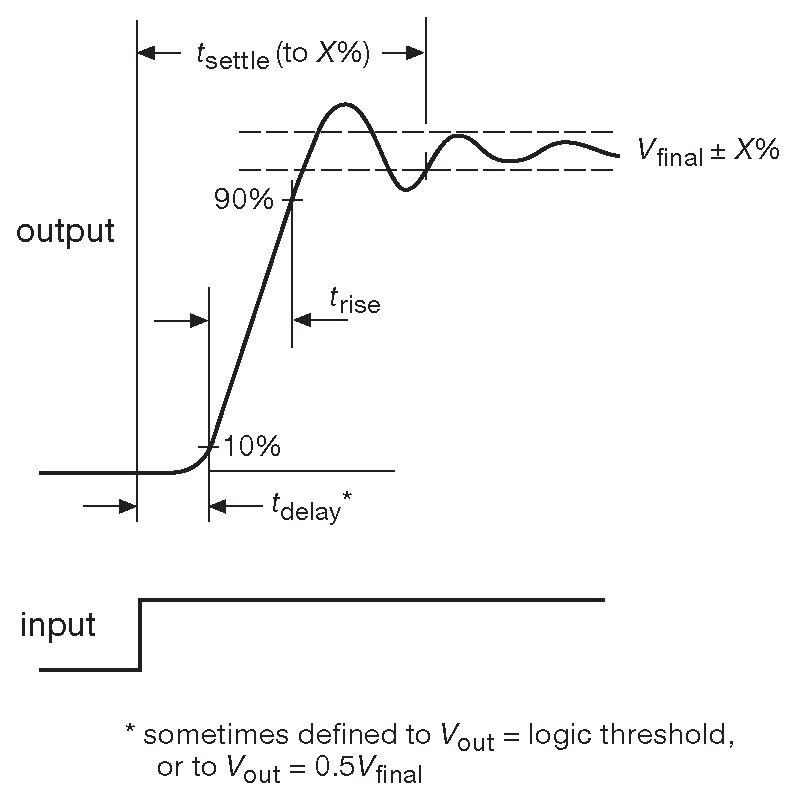
Рис.5.14 Время установления
Время установления ОУ можно выяснить, разобравшись предварительно с другой проблемой, а именно, что произойдёт с идеальным скачком напряжения, если его пропустить через RC фильтр нижних частот ( рис. 5.15 ). Этот простой пример показывает, что сигнал после фильтра совпадает с той самой кривой установления. Результат оказывается весьма полезен, потому что для борьбы с шумами рабочая полоса часто ограничивается фильтрами ( подробнее об этом чуть позже ). Рассмотренный пример легко распространить на операционные усилители. Достаточно вспомнить, что скорректированный ОУ имеет подобно RC фильтру спад 6 dB/octave на большей части частотного диапазона. Если охватить его петлёй обратной связи с усилением \( G_{cl}\) , то полоса пропускания ( т.е. частота, на которой петлевое усиление падает до единицы ) будет выражаться соотношением \( f_{3db}=f_T/G_{cl}\) .
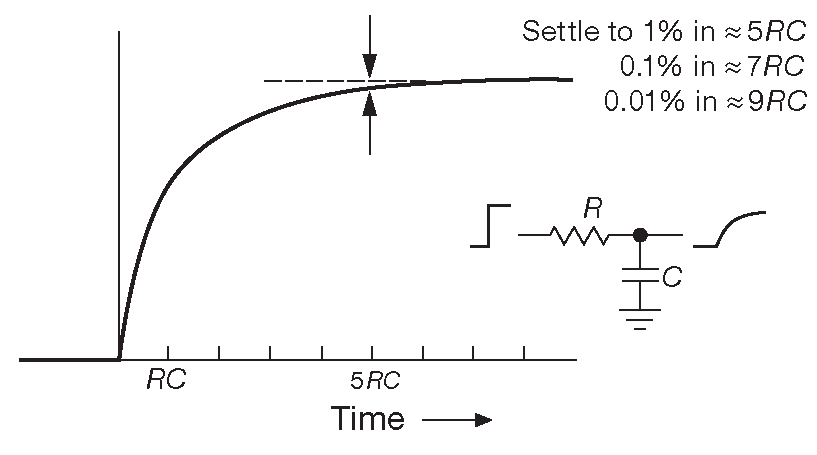
Рис.5.15 Время установления RC фильтра нижних частот
В общем случае система с рабочей полосой \( B\) имеет время отклика \(τ≈1/( 2πB ) \) , и, соответственно, эквивалентная «постоянная времени» усилителя равна \(τ≈ G_{cl}/( 2πf_T ) \) , а время установления - в районе 2...10\(τ\) .
Попробуем повторить данные рассуждения для реального компонента. Прецизионный операционный усилитель с малым временем установления TLE2141 фирмы TI имеет частоту единичного усиления \( f_T \)=5.9 MHz . Приведённая выше формула для инвертирующей конфигурации ( G=2 ) даёт время отклика 54 ns , а время установления до 0.1% ( 7\(τ\) ) - 378ns , что хорошо согласуется с паспортным значением 340 ns .
Предложенная схема имеет несколько недостатков.
- Простая модель даёт только нижнюю границу ожидаемого времени установления в реальной схеме и требует обязательной проверки ограничений, накладываемых скоростью нарастания, причём последние могут преобладать.
- Даже если скорость нарастания - не проблема, время установления может оказаться гораздо больше, чем идеальная модель первого порядка ( с одним полюсом ), и зависит оно от схемы коррекции и запаса по фазе.
- Сигнал на выходе ОУ будет успокаиваться быстрее, если фазочастотная характеристика цепи частотной коррекции в схеме без обратной связи показывает в двойном логарифмическом масштабе красивую ровную линию ( см. рис. 5.17 ), экземпляры с колебаниями на графике сдвига фазы с большей вероятностью будут иметь выбросы и звон как на верхнем графике на рис. 5.14 .
- Быстрое время установления, скажем, до 1% совершенно не гарантирует столь же быстрого установления до 0.01% , потому что у графика может быть длинный хвост ( рис. 5.16 ).
- Никакие теоретические рассуждения не заменят реальных измерений.
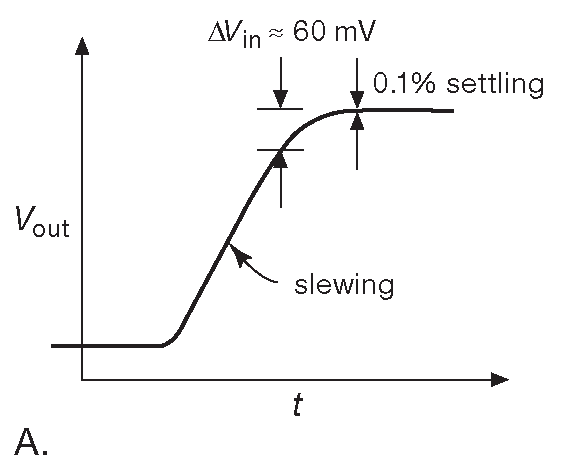
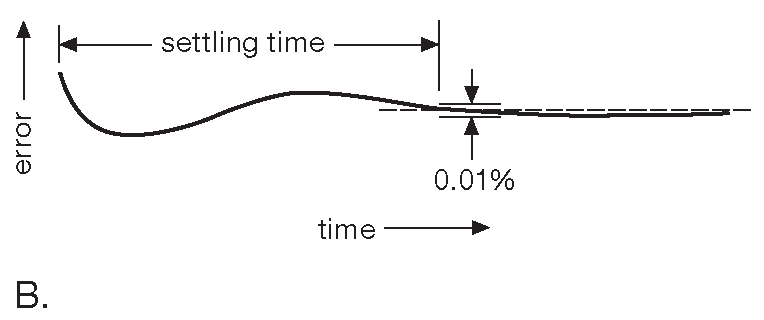
Рис.5.16 (A) Скорость нарастания снижается, когда ошибка на входе падает ниже уровня 60 mV . (B) Попадание в область малых отклонений может занять неожиданно долгое время
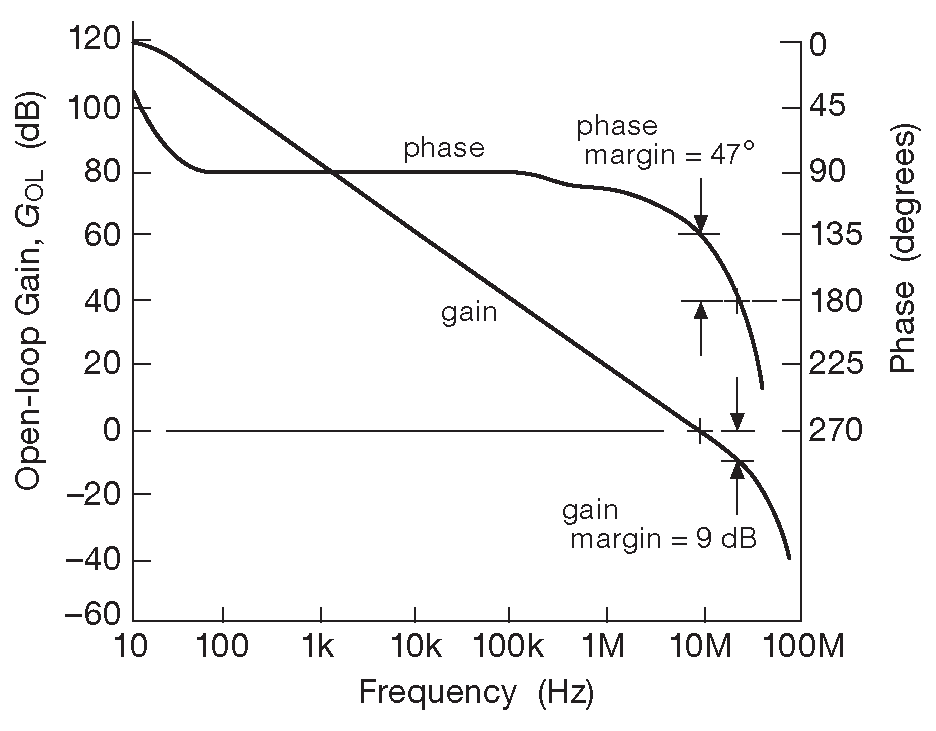
Рис.5.17 Зависимость усиления и фазы от частоты для OP-42
В табл. 5.4 перечислено некоторое количество быстрых операционных усилителей, подходящих для приложений, где требуется высокая частота единичного усиления \( f_T \) , высокая скорость нарастания, быстрое время установления и относительно небольшое напряжение смещения.
5.8.3 Переходные искажения и выходной импеданс
==310
В некоторых ОУ ( например, в классическом LM324/358 ) с однополярным питанием стоит простой двухтактный выходной каскад без компенсации двойного падения на диоде, см. §2.4.1 . Это ведёт к искажениям «класса-B» [* рис. 4.27 и 4.28 ] на выходе, потому что выходным транзисторам приходится преодолевать перепад 2\( V_{BE}\) когда выходной сигнал переходит через ноль ( рис. 5.18 ). Такие искажения могут быть очень заметны, особенно на высоких частотах, где падает петлевое усиление, см. данные измерений на рис. 5.19 . Этот недостаток существенно снижен в ОУ с выходными транзисторами, работающими в режиме небольшой проводимости ( «класс-AB» ), например, LT1013 - улучшенная версия LM324. Правильный выбор ОУ имеет очень большое значение для параметров звуковых усилителей с малыми искажениями. Возможно, именно эта проблема вносит основной вклад в «транзисторный звук», о котором говорят аудиофилы. Некоторые современные ОУ, особенно те, что предназначены для звуковых устройств, спроектированы для чрезвычайно низких переходных искажений. Примерами могут служить LT1028, AD797 и великолепная серия LME49000 фирмы TI/NSC. Например, LME49710 имеет менее 0.0001% искажений в полном звуковом диапазоне 20 Hz...20 kHz ( такие цифры заявлены, единственное, что остаётся - верить им! ). Все эти усилители имеют также очень низкое напряжение шума: LT1028, например, носит титул чемпиона мира по шуму ( \(e_n\)=1.7 nV/\(\sqrt{Hz}\) (max) на частоте 10 Hz ). Расширенные графики искажений ОУ на рис. 5.43 и 5.44 показывают, как разные усилители соревнуются за звание короля низких искажений. Высоковольтовые ОУ имеют преимущество ниже 10 kHz , а низковольтовые - выше 200 kHz .
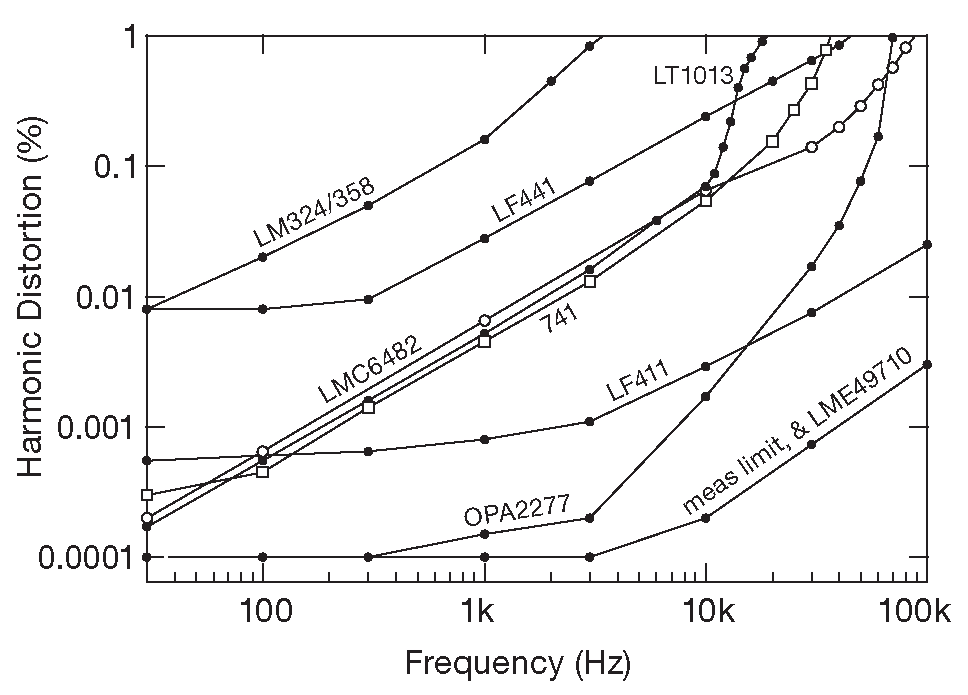
Рис.5.19 Результаты измерений коэффициента гармоник от частоты для нескольких популярных ОУ ( выходной сигнал 1 Vrms , без нагрузки ). См. также рис. 5.43 и 5.44
Выходной импеданс в цепи без обратной связи типового усилителя с разделёнными линиями питания имеет наибольшую величину, когда потенциал выхода находится вблизи земли, потому что выходные транзисторы работают при самом низком токе через заземлённую нагрузку. Выходной импеданс также растёт на высоких частотах, когда падает усиление транзисторов, и может слегка повышаться на очень низких частотах из-за температурной обратной связи внутри кристалла.
Разработчик очень часто упускает из виду выходной импеданс ОУ без обратной связи, думая, что эта самая обратная связь всё исправит. Считаем своим долгом напомнить, что выходное сопротивление некоторых ОУ составляет сотни ом и пренебрегать его воздействием нельзя, особенно если усиление невелико. Типовые графики выходного импеданса ОУ с обратной связью и без неё показаны на рис. 5.20 и 5.21 .
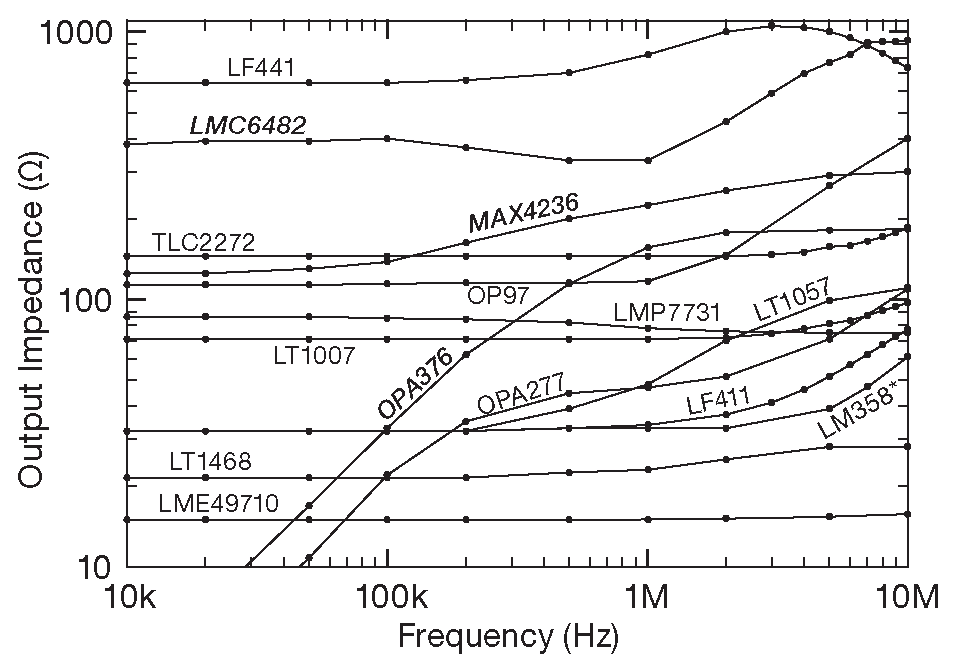
Рис.5.20 Результаты измерений выходного импеданса от частоты для некоторых ОУ. Компоненты, отмеченные жирным начертанием имеют КМОП выход. «LM358*» – с нагрузочным резистором, подключённым к отрицательной линии питания
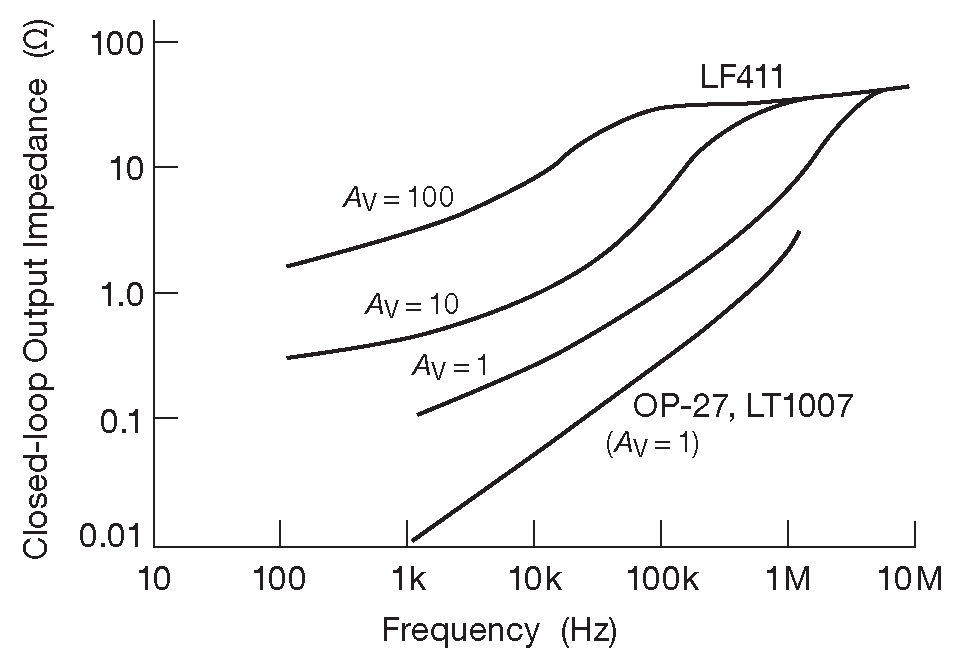
Рис.5.21 Зависимость выходного импеданса от частоты в цепи с замкнутой обратной связью для LF411 и LT1007 по данным производителей
Табл. 5.4 Основные представители высокоскоростных ОУ
==311
Конечное выходное сопротивление влияет также на устойчивость усилителя с емкостной нагрузкой ( §4.6.2 ). Именно оно, а вернее \(R_{out}\) в сочетании с \( C_{load}\) , отвечает за отставание фазы в цепи обратной связи. Несколько возможных решений проблемы показаны на рис. 4.78A - 4.78E , и среди них - разделение путей обратной связи и включение в цепь обратной связи буфера с единичным усилением. Рассмотрим последний вариант подробнее.
5.8.4 Умощняющий буфер с единичным усилением
==312
Если метод разделения путей обратной связи применить нельзя, можно вставить буфер с единичным коэффициентом усиления в петлю обратной связи, как это сделано в универсальном лабораторном усилителе на рис. 4.87 . LT1010, применённый там, имеет достаточную полосу ( > 10 MHz ), в которой добавляемый им сдвиг фаз невелик, а значит, потребует небольшой дополнительной компенсации при включении в цепь обратной связи.
Такие «умощнители» могут работать на нагрузку, требующую много тока ( например, коаксиальный кабель ), независимо от проблем с возможной дополнительной ёмкостью. Но, кроме того, они полезны в точных схемах, где токи невелики, потому что снимают с прецизионных усилителей тепловую нагрузку и связанный с ней дрейф. Примеры такого использования можно видеть на рис. 5.47 и 13.119 и в Части _4 .
5.8.5 Ошибки усиления
Есть ещё ошибка усиления в цепи с обратной связью, вызванная конечной величиной усиления ОУ.
В Части _2 ( §2.5.2 ) рассчитывался коэффициент усиления в цепи с обратной связью: G=A/(1+AB) , где A - усиление без обратной связи, а B - петлевой усиление в цепи обратной связи. Можно подумать, что если A > 100 dB или около того, то этого «должно быть достаточно для каждого», но, как только речь заходит о точных схемах, жизнь начинает преподносить сюрпризы. Из предыдущего уравнения легко вывести «ошибку усиления»: \[ \delta_G=gain\text_error≡\frac{G_{ideal}-G_{actual}}{G_{ideal}}\quad, \] или просто 1/(1+AB) . Её величина меняется от 0 при A=\(∞\) до 1 ( 100% ) при A=0 .
Упражнение 5.2
Выведите предыдущее выражение для ошибки.
Итоговая цифра, зависящая к тому же от частоты, даже близко не является «пренебрежимо малой». Например, у LF411 усиление на низкой частоте без обратной связи равно 106 dB . Для усиления на низкой же частоте с обратной связью и G=1000 ошибка будет составлять 0.5% . Ситуация на самом деле ещё хуже: выше 20 Hz усиление падает со скоростью 6 dB/octave , т.е. при 500 Hz ошибка вырастет до 10% ! На рис. 5.22 представлены расчётные графики ошибки усиления от частоты для коэффициентов G=1000 и G=100 для OPA277, имеющего выдающийся коэффициент усиления на постоянном токе 140 dB . Совершенно очевидно, что требуется высокое значение \( f_T \) и даже на средних частотах необходимо очень большое усиление.
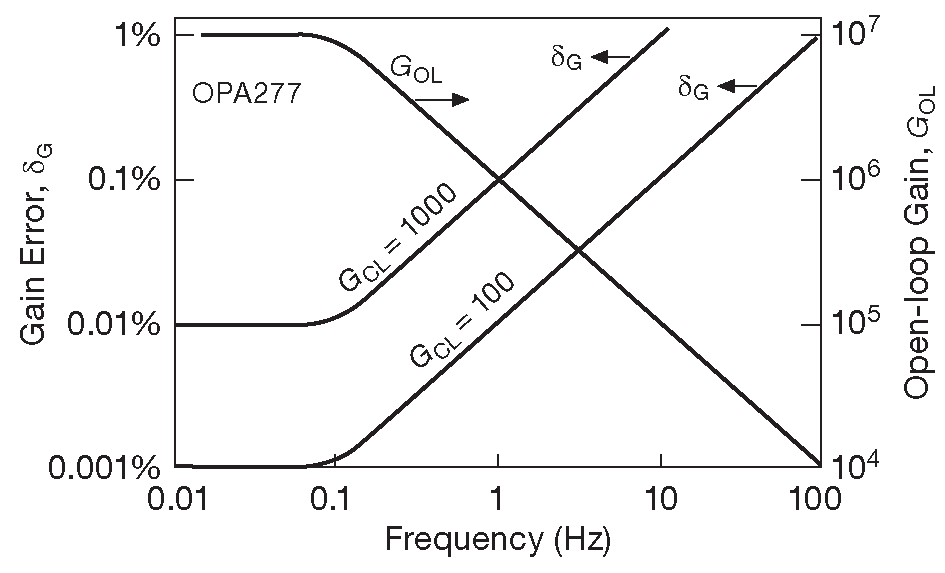
Рис.5.22 Ошибка усиления для OPA277
График построен по паспортным данным о зависимости усиления от частоты. Даже если в справочнике уже есть график, работать удобнее с усилением без обратной связи на постоянном токе и величиной \( f_T \) , т.е. по паспортному значению GBW , см. рис. 5.42 и сопровождающее его пояснение. Они дают цифры для интересующей частоты, а значит, и ошибку усиления как функцию частоты: \[ \delta_G=\frac{1}{1-jB( f_T/f)}≈\frac{f}{Bf_T} \quad , \] где B как обычно петлевое усиление в цепи обратной связи, а приближённое значение работает, если B·\(\frac{f_T}{f}\)≫1 . Следует помнить, что в некоторых случаях, например в фильтрах, B также может зависеть от частоты.
Упражнение 5.3
Выведите предыдущее равенство.
5.8.6 Нелинейность усиления
На низких частотах ОУ имеют большое усиление и избыточное отношение \( G_{OL}/G_{cl}\) в цепи обратной связи, влияющее на точность и подавление внутренних нелинейностей схемы, как говорилось в §2.5.3 . В идеале хотелось бы иметь в точной схеме достаточное усиление в цепи без обратной связи. Это та самая причина, по которой прецизионные усилители и ОУ с автоподстройкой нуля ( §5.11 ) имеют большое усиление, например, ∼160 dB для LMP2021 ( с автоподстройкой ) и ∼150 dB для LT1007 ( точный ).
==313
Чтобы увеличить точность, нужна большая величина петлевого усиления, а, чтобы увеличить линейность, петлевое усиление лучше иметь поменьше. Но, что влияет сильнее, так это исходная внутренняя линейность усилителя и её зависимость от выходной амплитуды ( если данное явление имеет место ). Внутренняя линейность прямо зависит от схемы выходного каскада и особенностей нагрузки. Безусловным недостатком являются переходные искажения и асимметрия в приёме/отдаче тока выходного каскада, как это происходит в LM358, где в верхнем плече стоит составной npn , а в нижнем - одиночный pnp транзистор. Плохая разводка кристалла может создавать нелинейности из-за термических смещений, появляющихся при нагреве током нагрузки.
Отличную серию измерений низкочастотной нелинейности усиления некоторого числа операционных усилителей ( к сожалению, только фирмы National Semiconductor ) провёл Боб Пиз ( Bob Pease ) 19 . Усилители включались по схеме инвертора с единичным коэффициентом и полным размахом выходного сигнала. Делалось два измерения: без нагрузки и с нагрузкой 1 kΩ . Базовая схема показана на рис. 5.23A . Осциллограф показывает ошибку между входным и выходным сигналами. Реальные измерения проводились по схеме 5.23B , где тестируемый усилитель сам увеличивал сигнал ошибки в 1000 раз, докладывая о неприятностях лично.
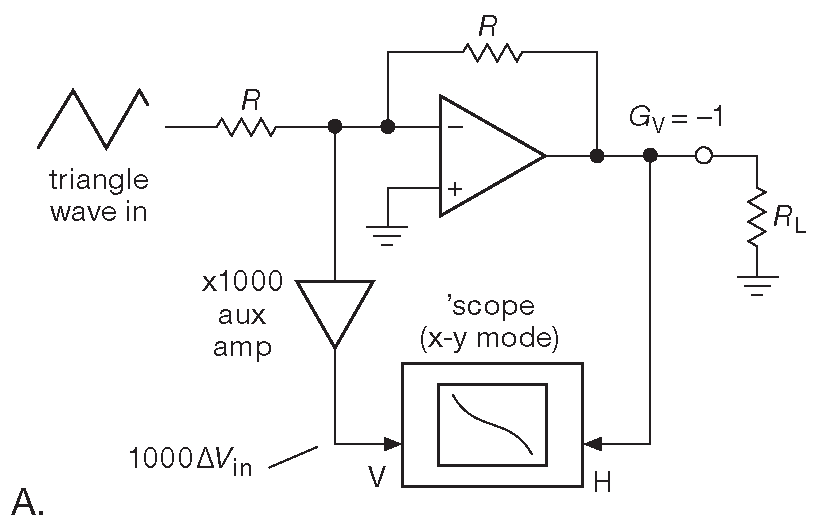
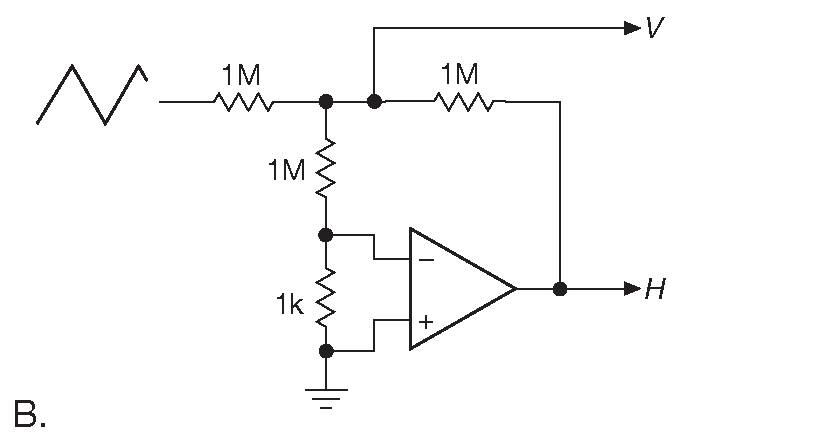
Рис.5.23 Схема проверки низкочастотной линейности усиления. (A) Принцип измерения: дополнительный усилитель позволяет увидеть зависимость микровольтового дифференциального входного напряжения от размаха сигнала на выходе. (B) Схема, которую Боб Пиз использовал при измерениях для ##AN-1485 ( см. сноску чуть выше в тексте )
Пара возможных отклонений для нагруженных ОУ показана на рис. 5.24 , где приведены полученные Пизом картинки для упомянутого LM358 ( несимметричный характер отдачи/приёма тока ) и LM8262 ( переходные искажения ). Образцовый LM4562 с очень низкими искажениями имеет идеально прямую почти горизонтальную линию. «Обычные ОУ» LF411 ( одинарный ) и LF412 ( сдвоенный ) имеют интересное различие: согласно измерениям Пиза разводка кристалла LF411 совершенством не блещет ( в терминах усиления и температурных эффектов ), а у LF412 она заметно лучше, что благоприятно отразилось на его параметрах.
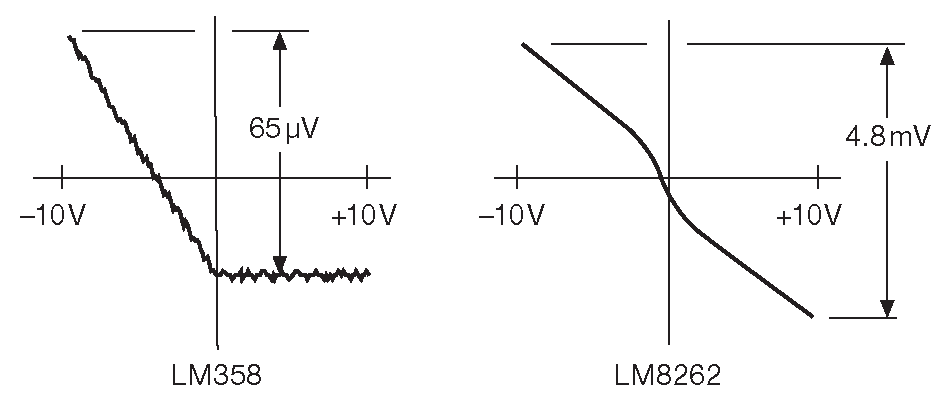
Рис.5.24 Нелинейность усиления двух ОУ со слабым выходным каскадом. На этих графиках по вертикальной оси показано малое дифференциальное входное напряжение, нужное для создания полного размаха сигнала на выходе - горизонтальная ось. Ошибка усиления получается делением величины вертикального отклонения от идеальной прямой линии на величину полного выходного перепада
Здесь даны некоторые из результатов Боба Пиза для ОУ, нагруженных на некоторую небольшую нагрузку ( 4 kΩ ). В общем случае измеренное значение нелинейности в ненагруженном состоянии было гораздо ниже, чем приведённые цифры. Следует учитывать, что измерения проводились на очень малых частотах ( в большинстве случаев всего несколько герц ), где петлевое усиление максимально.
==314
HV BJT ( V_sig=±10 V) LM8262 12 ppm xoverdist. LM358 1 ppm asym. output stage LE411 1.4 ppm poor layout - thermal LE412 0.3 ppm better layout LM4562 0.025 ppm pro-audio, G_ol = 107 CMOS RRO ( V_sig = ±4 V) LMC6482 1.1 ppm jellybean LMC6062 0.2 ppm precision CMOS auto-zero ( V_sig = ±2 V) LMP2012 0.2 ppm precision5.8.7 Фазовая ошибка и «активная компенсация»
До настоящего момента речь шла в основном об ошибках усиления, вызванных ограниченной рабочей полосой ( а значит, падением петлевого усиления с ростом частоты ). Но ограничение усиления вызывает ещё и фазовую ошибку, на которую надо обращать внимание при обработке видео, интерферометрии и т.д. Эффект, кстати, совсем не маленький: спад от одной RC секции создаёт сдвиг фазы ∼6° на частоте \( f_c\)/10 и ∼0.6° на \( f_c\)/100 ( §1.7.9 ). Последняя цифра относится к частоте, которая на две декады ниже частоты «-3dB». Если промоделировать спад усиления операционного усилителя в схеме без обратной связи ( спад от одного полюса ), то можно ожидать сравнимого сдвига фазы.
В таком уровне точности итоговый сдвиг фазы усилителя напряжения на ОУ выражается формулой \[ φ=\arctan\left(\frac{f}{f_c}\right )≈\frac{f}{f_c} \quad , \] где результат выражен в радианах, а \( f_c\) - частота, на которой петлевое усиление падает до единицы: \( f_c=f_T/G_{cl}\) . Здесь \( G_{cl}\) - усиление с обратной связью ( оно устанавливается цепью обратной связи ), а \( f_T \) - произведение усиления на полосу ( GBW ) усилителя. В случае спада, вызванного единственным полюсом на частотной характеристике, GBW совпадает с частотой единичного усиления ( на ней усиление без обратной связи падает до единицы ), но в типичном ОУ АЧХ имеет более сложную форму, и использовать GBW удобнее. Если умножить цифру на 180°/\(π\)=57.3° , то получим сдвиг фазы в градусах. Формула даёт достаточно точный результат для умеренного ( до 0.5 радиана ) сдвига фаз.
Указанная проблема решается несколькими способами. Самый простой - использовать усилитель с большей рабочей полосой. Если это нежелательно ( или невозможно ), то имеется второй способ: надо добавить в обратную связь RC цепь, чтобы скомпенсировать ошибку фазы ( в терминах «S-пространства» это компенсация нулём имеющегося полюса ). Метод вполне рабочий, но требует «настройки» компенсирующей цепи, чтобы подогнать её частотный отклик к параметрам конкретного операционного усилителя. Кроме того, параметры ОУ меняются с температурой, и так же должна себя вести компенсирующая цепь. Третий вариант - включить два последовательных каскада, каждый - с меньшим усилением ( а значит, и с меньшей фазовой ошибкой ).
Но самым красивым решением будет активная компенсация - приём, использующий второй согласованный ОУ, чтобы создать копию ошибки, которая затем вычитается из основного сигнала. Как это делается, показывает рис. 5.25 20 . Полоса основного усилителя не меняется, но ошибка фазы очень сильно уменьшается, что хорошо видно на данных моделирования и результатах реальных измерений на рис. 5.26 . АЧХ имеет небольшой выброс ( около +3dB ) на частоте, где сдвиг фазы достигает 45° , но в диапазоне малых фазовых ошибок он совершенно незначителен ( +0.1 dB на частоте \( f \)=0.1\( f_T/G_{cl}\) ). Снижение коэффициента усиления в схеме с замкнутой обратной связью ведёт к росту выброса 21 . Если считать усилители согласованными, то использование такого приёма даёт сдвиг фаз ( в радианах ): \[ φ≈\left(\frac{f}{f_C}\right )^3 \quad . \]
Результат достаточно точен при умеренных сдвигах фазы ( < 30° ).
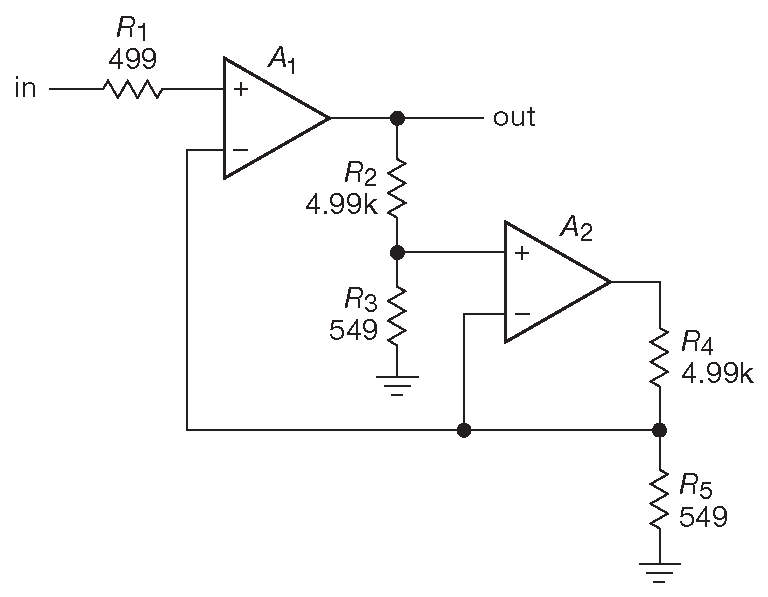
Рис.5.25 Уменьшение сдвига фазы после «активной компенсации» за счёт близко совпадающих частотных характеристик двух половинок сдвоенного усилителя \( A_1-A_2\)
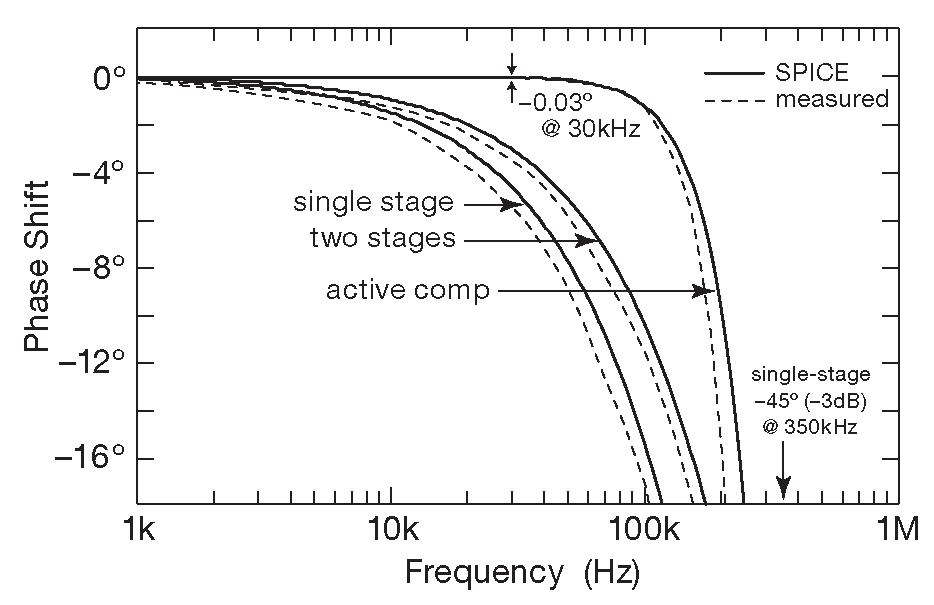
Рис.5.26 Результаты моделирования в SPICE и данные измерения сдвига фазы в зависимости от частоты для схемы 5.25 , собранной на сдвоенном ОУ LF412. Для сравнения те же данные сняты для одного усилителя с G=\(10\) и двух последовательных каскадов с G=\(\sqrt{10}\) каждый. По данным измерения \( f_c\) используемой микросхемы составила 295 kHz , что несколько ниже, чем данные модели - 350 kHz
==315
Реальные операционные усилители согласованы не слишком хорошо, и, чтобы выяснить влияние \( f_T \) на уровень компенсации сдвига фаз, было запущено моделирование с 10%-разбросом \( f_T \) ( рис. 5.27 ). Похоже, тестовые экземпляры, выбранные достаточно случайно ( т.е. пальцами из коробки: открыть, достать, измерить ), имели хорошую степень согласования, что отмечалось и Вонгом: «Однокристальные сдвоенные или счетверённые операционные усилители показывают уровень согласования ( в пределах 1..2% ) достаточный для использования в схеме активной обратной связи» 22 .
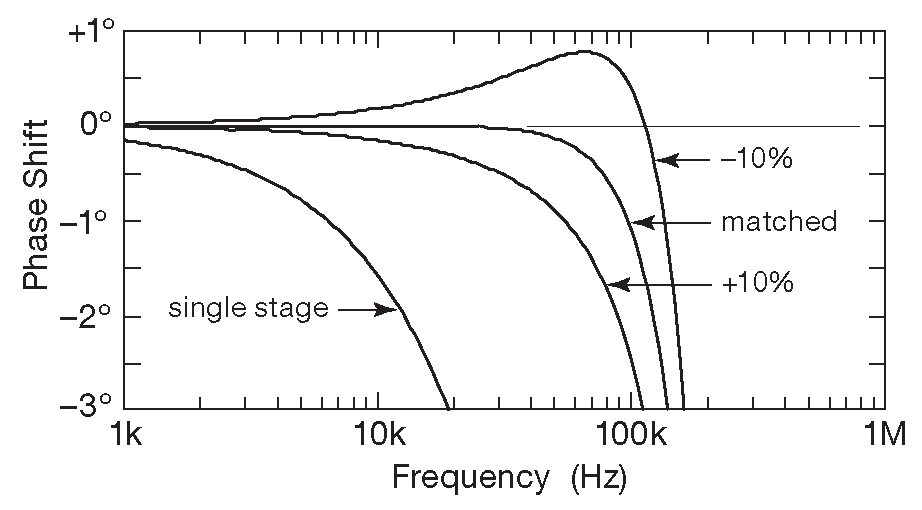
Рис.5.27 Активная компенсация сдвига фазы требует согласованных частотных характеристик ОУ, что видно на результатах моделирования 10%-разницы \( f_T \) в SPICE
Интересно сравнить предсказанный сдвиг фаз для четырёх ситуаций, перечисленных в начале:
- одиночный усилитель с известной рабочей полосой, назовём её \( f_{T0}\) ( 3 MHz для LF412 ), включённый по схеме с обратной связью с усилением G=10 ;
- два последовательных каскада, каждый с усилением G=\(\sqrt{10}\) ;
- схему с активной компенсацией ( рис. 5.25 ); и
- одиночный усилитель со значительно большей рабочей полосой ( 10 \( f_{T0}\) ) .
Результаты расчётов таковы:
Single, 2-stage, Active, Single, G=10 each G^VT0 comp /?=10/?? 0.001 /to —0.57° —0.36° —0.00006° —0.006° 0.003/to —1.7° —1.1° —0.0015° —0.17° 0.01/to —5.7° —3.6° —0.06° —0.57° 0.03 /to —17.2° —10.9° —1.5° —1.7° 0.1 /to —45° —36° —45° —5.7°Отсюда ясно, примечательная ( но малораспространённая ) техника активной компенсации позволяет эффективнее использовать ресурсы. Неинвертирующий каскад с G=2 прямо напрашивается на раскачку 75-омного видео кабеля в схеме с последовательным согласованием 23 .
==315
18 Схема слегка упрощена. В оригинальном LM101 Видлара ( Widlar ) входной каскад представляет собой усилитель с общей базой на дифференциальной pnp паре с npn повторителями на входах. ) <-
19 Пример по применению фирмы National Semiconductor “AN-1485: The Effect of Heavy Loads on the Accuracy and Linearity of Operational Amplifier Circuits” ( «Влияние больших нагрузок на точность и линейность схем на операционных усилителях» ) или "What’s All this Output Impedance Stuff, Anyhow?" ( «Что это вообще такое - 'выходной импеданс'?» ). Данные по нелинейности иногда можно найти в паспортных данных, см. AD620. <-
20 См. статью Джеймса Ванга “Active Feedback Improves Amplifier Phase Accuracy”, J. Wong, EDN Magazine, 17 Sept 1987, перепечатанную как AN-107 фирмы Analog Devices. Вонг почерпнул эту идею у Солимана ( Soliman ) в статье 1979г., а тот в свою очередь от Бракета и Седра ( Brackett & Sedra) в публикации 1976г. Так или иначе, именно статья Вонга наиболее информативна и хорошо объясняет схему 5.25 . <-
21 Моделирование в SPICE показывает, что для LF412 при коэффициенте усиления G=2 выброс увеличивается до ∼7 dB . Купировать проблему можно корректирующим конденсатором \( C_C\) , включённым параллельно резистору \(R_2\) . Выбор номинала \( C_C\) в соответствии с \( f_T \) ОУ ( т.е. \( C_C=1/( 2πf_TR_2 )\) ) снижает выброс до 4 dB ценой утроения фазовой ошибки, впрочем, изначально довольно маленькой. В своей статье Джеймс Вонг указывает на возможную неустойчивость усилителя в таком включении при малых коэффициентах усиления ( ниже G=5 ). Кроме того, он объясняет, как дополнительно улучшить параметры схемы, собрав \( A_2\) из двух усилителей. <-
22 Результаты измерения содержимого коробки с LF412 показали, что, хотя значение \( f_T \) для различных корпусов имело разброс ±20% , два усилителя внутри микросхемы совпадали с точностью 0.1% . Правда, нашёлся-таки один отщепенец, показавший 1.5% . <-
23 И с двойным согласованием как на рис. 12.113 . Можно использовать любой нужный ОУ, позаботившись предварительно о согласовании парного усилителя с помощью резистора 150 Ω . <-