13.14 Псевдослучайные битовые последовательности и генерация шума
==974
13.14.1 Цифровая генерация шума
Интересная смесь цифрового и аналогового подходов обнаруживается в теме псевдослучайных битовых последовательностей - PRBS 135 . Оказывается, создавать последовательности битов или слов с хорошей степенью случайности достаточно легко. Речь идёт о последовательностях с определёнными вероятностными и корреляционными свойствами как в идеальном автомате для подбрасывания монеты. Из-за того, что указанная задача выполняется стандартным предсказуемым логическим элементом - сдвиговым регистром, результат получается предсказуемым и повторяемым, хотя для стороннего наблюдателя любая часть такой последовательности выглядит как случайный набор нулей и единиц. Всего несколько микросхем позволяют создавать последовательности, которые будут тянуться без повторений веками. Таким образом, имеем удобный и привлекательный метод получения аналогового шума. При проверке уровня ошибок ( BER ) в последовательных каналах и получении «глазковых» диаграмм ( рис. 12.132 и рис. 14.33 ) обычно используют PRBS. Такие же генераторы используются при предсказуемом кодировании ( или скремблировании от «scramble» ) последовательных данных в гигабитных Ethernet каналах. Это нужно для получения переменного сигнала для трансформаторных развязок в физическом канале. На приёмной стороне та же синхронная псевдослучайная последовательность удаляется с помощью операции XOR, которая восстанавливает исходные данные.
==975
13.14.1.A Аналоговый шум
С помощью простого ФНЧ из PRBS можно создать белый шум с гауссовым распределением, ограниченный по полосе, т.е. вплоть до определённой частоты шумовое напряжение будет иметь плоский спектр мощности (шум подробно рассматривается в Части _8 ). Тот же результат можно получить, суммируя данные на отдельных разрядах сдвигового регистра с индивидуальными весовыми коэффициентами ( с помощью резисторов разных номиналов ), т.е. проводя цифровую фильтрацию. Таким образом, легко можно получить шум с плоским спектром и верхней рабочей частотой до нескольких мегагерц. Как будет ясно из дальнейшего, цифровые источники шума имеют много преимуществ перед чисто аналоговыми методами - диодами и резисторами.
13.14.1.B Другие приложения
Помимо очевидного использования в качестве источников аналогового шума псевдослучайные последовательности используются в приложениях, не имеющих ничего общего с шумом. К ним относятся тестовые последовательности для проверки последовательных линий связи ( глазковые диаграммы, проверка на ошибки в канале ) и для скремблирования ( как замену шифрованию ) в сетевых протоколах типа Ethernet. Они используются в широкополосных схемах связи с подавлением несущей, где каждый быт передаётся в виде определённого сочетания коротких пачек кодированных импульсов . Такой метод используется в сотовой связи стандарта CDMA, системе кодирования сигнала в GSM и при передаче цифрового телесигнала. Такие последовательности используются в проверочных и корректирующих кодах, потому что они позволяют такое преобразование блоков данных, при котором корректные данные разделяет наибольшая «дистанция Хемминга» ( измеряемая числом однобитовых ошибок ) [*] . Автокорректирующий характер псевдослучайных кодов определяет удобство модуляции ими радарных сигналов. [**] . Принимаемый эхо-сигнал сравнивается ( точнее проходит процесс кросс-корреляции ) с переданной последовательностью. Наконец, такие коды можно использовать в делителях «по-модулю-n» .
[*]
[* проще говоря, сколько битовых ошибок надо наложить на правильно закодированный элемент данных, чтобы он превратился в другой правильный элемент, т.е. элемент, который система примет в качестве правильного, но который на самом деле есть результат деструктивного воздействия серии ошибок. Для обычной системы контроля чётности дистанция Хемминга равна двум.
[**]
[* КРЕТ-то, поди, свою систему РЭБ строит на внесении беспорядка в такие сигналы].
13.14.2 Битовые последовательности на сдвиговых регистрах с обратными связями
Самые простые и популярные генераторы псевдослучайных последовательностей делаются на сдвиговых регистрах с линейными обратным связями ( LFSR , рис. 13.111 ). Сдвиговый регистр длины m бит тактируется некоторой частотой \( f_0\) . Элемент «ИСКЛЮЧАЮЩЕЕ-ИЛИ» проводит одноимённую операцию ( сложение «по-модулю-2» ) над промежуточным n-ным и выходным m-ным битами, а результат подаёт на вход регистра. Такая схема проходит через последовательность состояний, которая определяется длиной регистра и повторяется через K тактов.
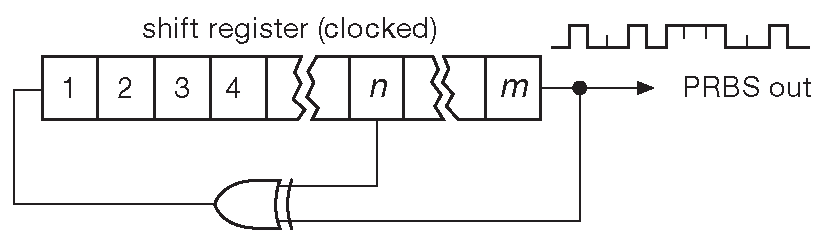
Рис. 13.111 Генератор псевдослучайной последовательности
Максимальное число возможных состояний m-разрядного регистра K=2m , т.е. число возможных сочетаний m чисел с двумя возможными значениями. К сожалению, состояние «все нули» зацикливается такой схемой, потому что «ИСКЛЮЧАЮЩЕЕ-ИЛИ» воспроизводит «0» на входе регистра. Таким образом, максимальная длина битовой последовательности такой схемы 2m—1 . Очевидно, что такой результат можно получить, если m и n выбраны корректно, и итоговая последовательность и в самом деле псевдослучайная 136 . В качестве примере рассмотрим 4-разрядный регистр с обратной связью ( рис. 13.112 ). Пусть он начинает работу с состояния 1111 ( оно может быть любым, кроме 0000 ), тогда имеет место следующая последовательность:
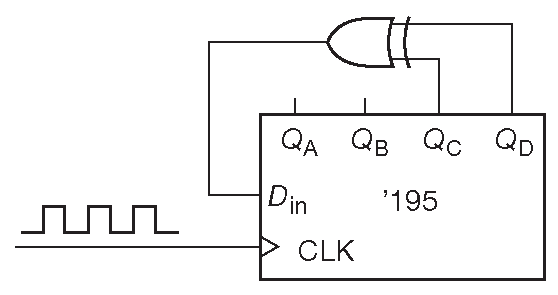
Рис. 13.112 4-разрядный сдвиговый регистр с линейными обратными связями ( 15 состояний, m=4, n=3 )
↱ → 1111 → 0111 → 0011 → 0001 → 1000 → 0100 → 0010 → 1001 →
→ 1100 → 0110 → 1011 → 0101 → 1010 → 1101 → 1110 → ↰
Состояния регистра записаны в формате \(Q_AQ_BQ_CQ_D\) . Схема имеет 15 различных состояний ( 24–1 ), после прохождения которых цикл повторяется. Следовательно, данный регистр является регистром максимальной длины.
==976
Упражнение 13.8
Покажите, что регистр с отводами от второго и четвёртого выхода не является регистром максимальной дины. Сколько всего имеется различных последовательностей [* при подключении обратных связей к другим выводам ] . Сколько состояний в каждой?
13.14.2.A Отводы для обратной связи
Регистр максимальной длины можно собрать с помощью элемента «ИСКЛЮЧАЮЩЕЕ-ИЛИ» и при большем двух числе отводов ( в этом случае надо использовать вентили «ИСКЛЮЧАЮЩЕЕ-ИЛИ» в виде стандартного дерева вычисления чётности, т.е. последовательного сложения «по-модулю-2» нескольких разрядов ). Для некоторых m последовательность максимальной длины можно получить, только используя три и более отвода. В табл. 13.14 перечислены все двухотводные последовательности максимальной длины до 167 бит включительно. Как и в предыдущем примере схема получается при суммировании вывода с номером n и последнего - m-ного по счёту. таблица содержит m, n и K - длину последовательности. В некоторых сочетаниях m и K имеются несколько различных последовательностей максимальной длины, различающиеся номером отвода n , поэтому всегда указывается пара m|n . Для примера с 4-разрядным регистром отвод можно делать и для n=3 , и для n=1 , т.е. есть пары 4|3 и 4|1 . Стандартные сдвиговые регистры имеют длину, кратную 8 [* и 4 ] , и если есть желание использовать все разряды, то придётся складывать более двух битов. Волшебные цифры приведены в табл. 13.15 .
Регистры с длиной большей 32 бит требуются редко: при частоте тактирования 1 MHz время повторения последовательности около часа. Для длины 64 бита и частоты 1 GHz на второй круг она пойдёт через шестьсот лет.
13.14.2.B Свойства последовательностей максимальной длины на сдвиговых регистрах с обратными связями
Очередной псевдослучайный бит создаётся в регистре с приходом активного фронта тактового сигнала и выдвигается наружу вслед за предыдущими элементами последовательности. Брать его можно из любого разряда регистра, но обычно используют последний (m-ный ). Последовательности максимальной длины на сдвиговых регистрах обладают следующими свойствами.
- В каждом полном цикле из K тактов число единиц на одну больше числа нулей. Дополнительная единица появляется из-за исключения состояния «все нули». Это значит, что появление и единицы, и нуля равновероятно ( дополнительная единица совершенно незаметна на фоне общего числа состояний сколь-нибудь длинного регистра: один цикл 17-разрядного регистра состоит из 65536 единиц и 65535 нулей ).
Table 13.14 Single-tap LFSRs
Table 13.15 Multiple-of-8 LFSRs
==977
- В одном полном цикле ( K тактов ) половина общего числа фрагментов из одних единиц имеет длину 1 , четверть - длину 2 , одна восьмая - длину 3 и т.д. Число фрагментов, состоящих из одних нулей, равно числу фрагментов из одних единиц такой же дины, исключая один пропущенный нуль. Это означает, что вероятность появления нуля или единицы не зависит от значения предыдущего бита, т.е. вероятность завершения фрагмента из одинаковых цифр равна 1/2 ( в противоположность тому, что понимается под «законом о среднем» обычным человеком с улицы [* а что думает о завершении серии символов «человек с улицы»? ] ).
-
Если одна последовательность полной длины ( K тактов ) сравнивается с тем же набором нулей и единиц, циклически сдвинутым на какое-либо число тактов n ( где n не равно 0 и не кратно K ), число несовпадений будет на единицу больше числа совпадений. Или та же мысль в строгой форме: автокоррелирующая функция является дельтой Кронера при нулевой задержке и –1/K во всех остальных случаях. Отсутствие боковых «лепестков» автокоррелирующих функций делает их очень удобными для использования в радарах [*ну, точно! КРЕТ именно тут
гадитработает ] .
Упражнение 13.9
Покажите, что 4-разрядная последовательность, показанная ранее ( отводы n=3, m=4 ) удовлетворяет этому условию. За выход взять бит \(Q_A\) : 100010011010111 .
13.14.3 Генерация аналогового шума с помощью последовательностей максимальной длины
13.14.3.A Преимущества цифровой генерации шума
Как отмечалось ранее, цифровой выходной сигнал сдвигового регистра с обратными связями можно превратить в белый шум с ограниченной полосой с помощью ФНЧ с частотой среза, лежащей гораздо ниже тактовой частоты. До погружения в технические подробности отметим некоторые преимущества цифровой генерации аналогового шума. Среди прочего такой способ позволяет создавать шум с известным спектром и амплитудой ( см. пример в §8.12.4.A ) и вдобавок с изменяемой рабочей полосой ( которая прямо зависит от тактовой частоты ) на простом надёжном цифровом устройстве. У данного метода нет проблем с разбросом параметров как в генераторах на шумовых диодах, нет наводок на чувствительную слаботочную схему на резисторе или диоде. Наконец, жёсткая заданность последовательности позволяет получить с помощью взвешенного цифрового фильтра повторяемую, независимую от тактовой частоты ( т.е. рабочей полосы ) форму шумового сигнала.
13.14.4 Спектр мощности последовательностей на сдвиговых регистрах
Выходной спектр, создаваемый сдвиговым регистром, состоит из шума начинающегося с частоты повторения полной последовательности \( f_{clk}\space \)/K и уходит выше частоты тактирования \( f_{clk} \) . Он ровный в пределах ±0.1 dB до частоты 0.12 \( f_{clk} \) и начинает довольно быстро падать выше точки «-3dB» ( 0.44 \( f_{clk} \) ). Таким образом, ФНЧ с частотой среза на уровне 5...10% тактовой частоты превратит выходной сигнал со сдвигового регистра в аналоговый шум с ограниченной полосой. Достаточно простого RC фильтра, но если нужны очень точные границы, то могут потребоваться активные фильтры с крутыми срезами ( см. Часть _6 ).
Рассмотрим выходной сигнал сдвигового регистра и его спектр мощности. В обычной ситуации постоянные смещения нежелательны, поэтому для «0» берётся напряжение –a , а для «1» +a ( рис. 13.113 ). Делать это можно разными способами, некоторые из которых показаны на рис. 13.114 .
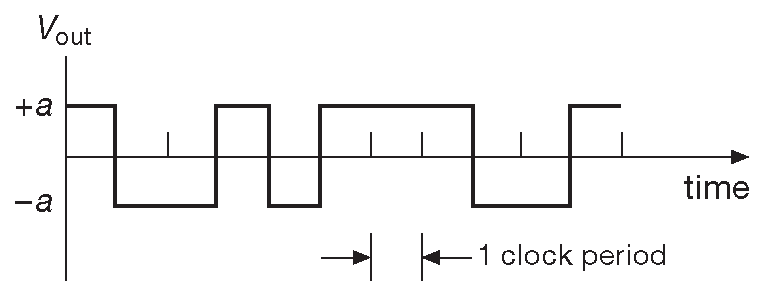
Рис. 13.113 Симметричные относительно земли логические уровни избавляют PRBS от постоянной составляющей
- С помощью аналогового КМОП ключа 'HC4053, работающего с двумя питаниями и потенциалам +a и –a на входах.
- С помощью быстрого ОУ с компенсацией тока постоянного смещения в суммирующей точке.
- С помощью быстрого компаратора, работающего от разделённого источника ±a вольт.
- С помощью КМОП логического элемента, питающегося от источников ±a вольт в делителем на входе. И, наконец,
- тот же логический элемент, включённый по переменному току с диодным ограничителем.
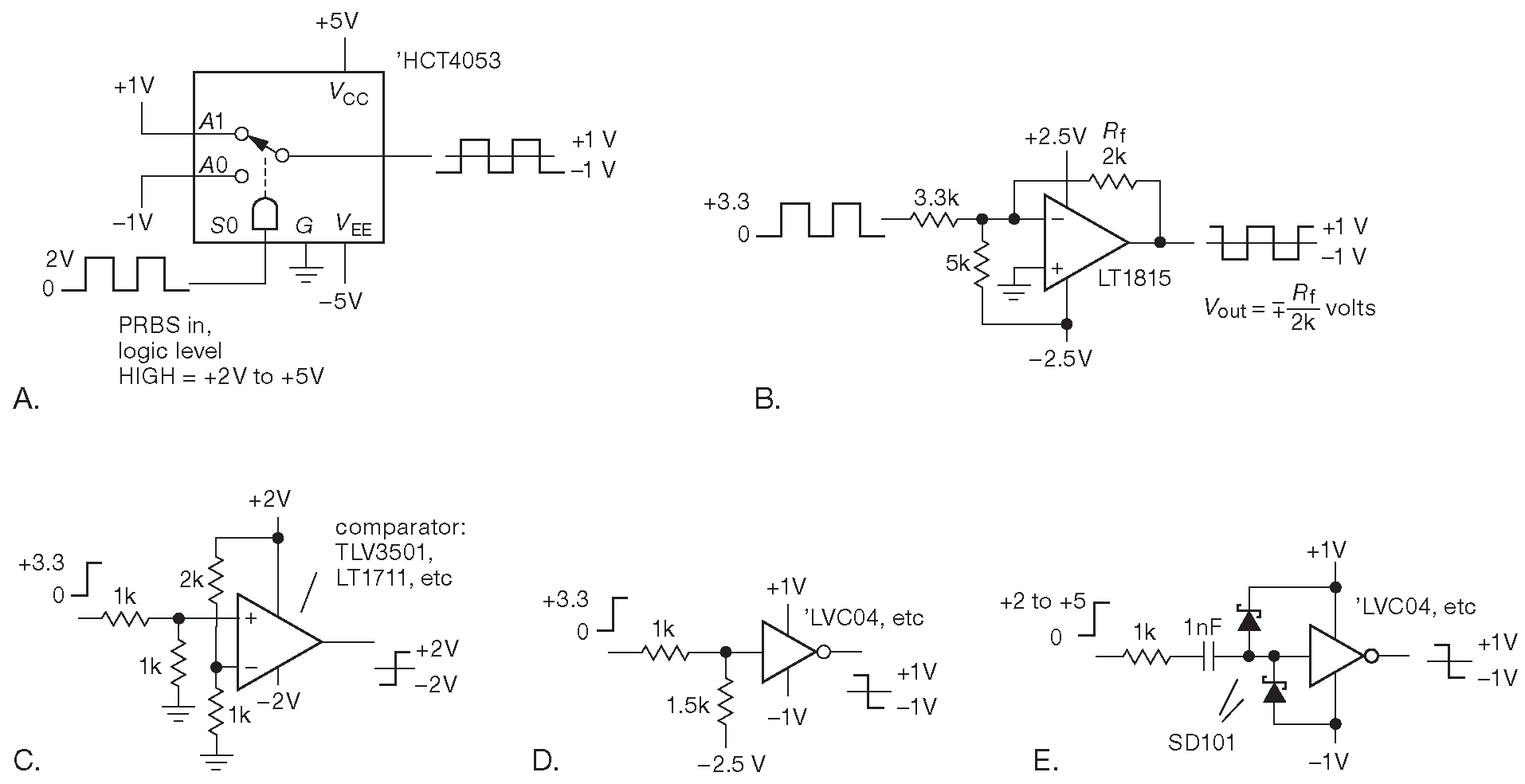
Рис. 13.114 Преобразование уровней позитивной логики в симметричный сигнал
Варианты с логическим элементом несколько переусложнены и допустимы, только если общее питание ( \( V \) =2a ) попадает в диапазон питания стандартных логических семейств ( 1...5 V ), зато тут всё хорошо со скоростью переключения. Последний вариант не имеет связи по постоянному току и требует, чтобы логический вход постоянно находился в каком-либо корректном состоянии, но здесь данное условие выполняется: PRBS не может замереть дольше, чем на m тактов 137 .
Как уже говорилось ранее, цепочка выходных битов имеет единственный пик автокорреляционной функции. График цифровой дискретной автокорреляционной функции ( сумма произведений соответствующих битов, когда последовательность сравнивается со своей сдвинутой копией и имеет на выходе только +1 и –1 ), показан на рис. 13.115 .
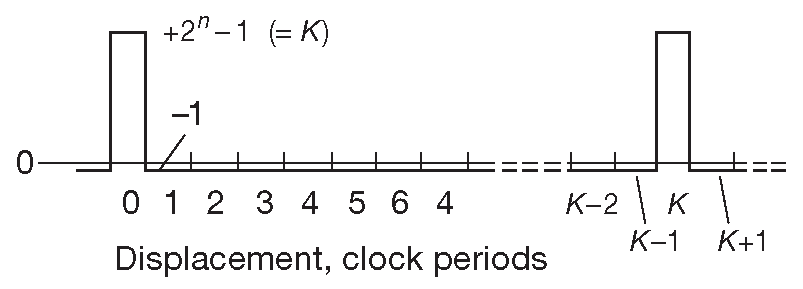
Рис. 13.115 Полный цикл дискретной автокорреляционной функции для последовательности максимальной длины на сдвиговых регистрах
==978
Её не следует путать с непрерывной автокорреляционной функцией, которая будет рассмотрена позднее. Приведённый график определён только для сдвигов на целое число тактов. Для всех тактов, чей номер не кратен периоду повторения K , автокорреляционная функция имеет постоянное значение –1 ( потому что в последовательности есть лишняя единица ). Это смещение совершенно незначительно по сравнению с величиной K у функции без смещения [* для кратных K значение равно K , а сумма [(+1)×K] + [(‐1)×(K–1)] =1 , ибо состояние «все нули» исключено ] . Аналогично, если рассматривать неотфильтрованный выход сдвигового регистра как аналоговый сигнал ( имеющий только два значения +a и –a ) [* и теперь непрерывный во времени: цифровой сигнал имеет разрывы графика на каждом фронте - вертикальных соединений там нет ] , нормализованная автокорреляционная функция станет непрерывной, и её график будет соответствовать рис. 13.116 . Другими словами, сигнал совершенно не коррелирован [* не совпадает ] сам с собой при сдвиге копии на ненулевое [* но не кратное K ] число тактов вперёд или назад.
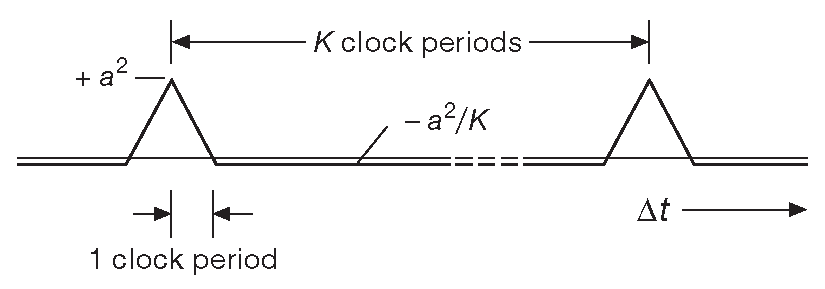
Рис. 13.116 Полный цикл непрерывной автокорреляционной функции для последовательности максимальной длины на сдвиговых регистрах
Спектр мощности неотфильтрованного цифрового выхода можно получить из коэффициента автокорреляции с помощью стандартных математических методов. Результатом будет серия равномерно расположенных пачек пиков ( дельта-функций ), которые повторяются через промежутки \( f_{clock}\space \)/K [* на рис. 13.117 они обозначены «spikes separated by..» ] , начиная с частоты повторения полной последовательности \( f_{clock}\space \)/K . Линейчатый характер спектра отражает тот факт, что последовательность с течением времени повторяет саму себя. Пугаться не надо: спектр будет непрерывным для любого измерения, продолжающегося меньше, чем длительность одного периода повторения псевдослучайной последовательности. Огибающая нефильтрованной цифровой последовательности ( волновой конверт ) показана на рис. 13.117 и соответствует квадрату функции \( (\sin x)/x \) . Отметим присущую ей особенность - отсутствие мощности шума на частоте тактирования и её гармониках.
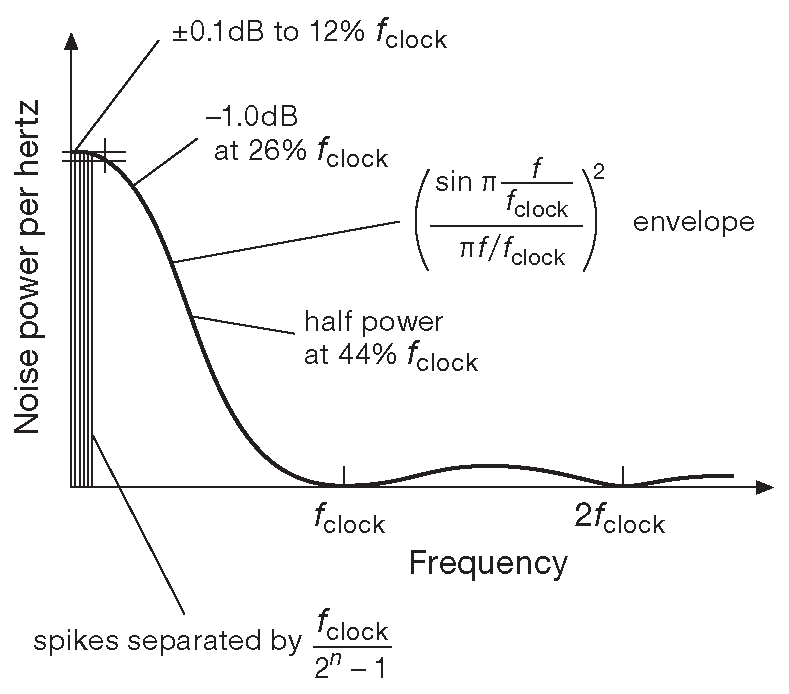
Рис. 13.117 Спектр мощности неотфильтрованной цифровой последовательности на выходе сдвигового регистра
13.14.4.A Напряжение шума
При генерации аналогового шума используется только некоторая низкочастотная область спектра. Для среднеквадратического напряжения шума уравнение его мощности выглядит так: \[ Vrms =a\left(\sqrt{\frac{2}{f_{clock}}}\right ) \qquad \mathrm{V/\sqrt{Hz}} \qquad ( f ≤0.2f_{clock}\space). \]
[* Среднеквадратическое напряжение имеет размерность [Вольты] и вычисляется по формуле \(e_n×\sqrt{BW}\) , где \(e_n\) - плотность напряжения шума, а BW - полоса, в которой ведётся измерение. Таким образом, для псевдослучайной битовой последовательности с амплитудой A вольт правильная формула выглядит так: \[ Vrms =A\left(\sqrt{\frac{2}{f_{clock}}}\right )×\sqrt{BW} \qquad \mathrm{V} \qquad ( f ≤0.2f_{clock}\space). \] См. §8.13 . Собснно, ниже даётся правильный расчёт для схемы 13.118 ].
==979
Это выражение верно для нижней половины спектра, т.е. той его части, которую обычно используют. Чтобы рассчитать плотность мощности в произвольной точке надо подставить в выражение функцию волнового конверта.
Например, предположим, что сдвиговый регистр тактируется частотой 1 MHz и размах сигнала на выходе ±10 V . Выход заводится на простой RC фильтр с \( f_{3dB} \) =1 kHz ( рис. 13.118 ). Посчитаем среднеквадратическое напряжение шума. Из предыдущего уравнения известно, что среднеквадратический шум [* плотность напряжения шума ] на выходе регистра 14.14 mV/\(\sqrt{Hz}\) . Из §8.13 известно, что полоса идеального фильтра составит (\(π\)/2)(1.0 kHz) или 1.57 kHz [* см. уравнение [8.55] ] . Следовательно, выходное напряжение шума составляет \( Vrms \) =0.01414 \(\sqrt{1570}\space\)=560 mV с формой спектра, соответствующей АЧХ RC фильтра нижних частот.
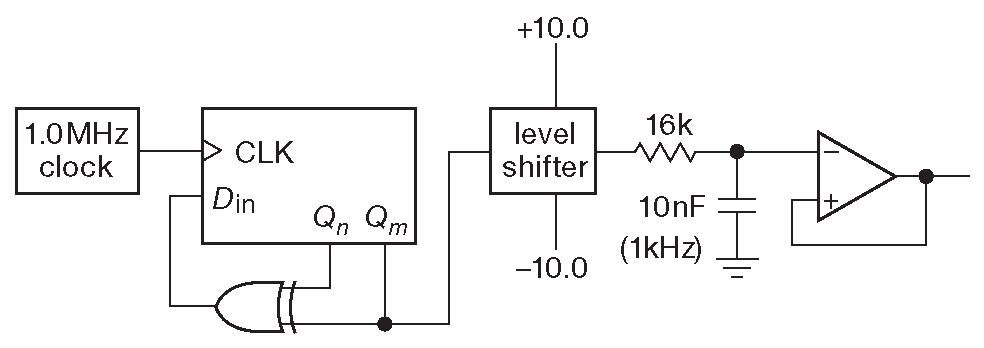
Рис. 13.118 Простой источник псевдослучайного шума
13.14.5 Фильтрация по низким частотам
13.14.5.A Аналоговая фильтрация
Спектр удобного для использования шума из генератора псевдослучайной последовательности начинается с нижнего предела периода повторения ( \( f_{clock}\space\)/K ) и простирается до верхнего предела, составляющего приблизительно 20% от тактовой частоты ( на этой частоте плотность мощности шума падает на 0.6 dB/\(\sqrt{Hz}\) ) . Предыдущий пример показывает, что простого фильтра из одной RC секции достаточно, если его частота \( f_{3dB} \) лежит заметно ниже тактовой частоты ( например, составляет 1% от \( f_{clock} \) ) . Если требуется полнее использовать тактовую частоту сдвигового регистра, придётся взять фильтр с более крутым срезом, например, Баттерворта или Чебышева. В таком варианте степень гладкости АЧХ результирующего спектра будет зависеть от характеристик фильтра, которые следует измерять, т.к. разброс параметров компонентов вызывает пульсации и неравномерность характеристики в полосе пропускания. Аналогично, если требуется точное значение плотности шума, надо измерять реальное усиление фильтра по напряжению.
13.14.5.B Цифровая фильтрация
Недостатком аналоговой фильтрации является необходимость перестройки частоты среза при серьёзном изменении тактовой частоты. Если делать это приходится часто, то помочь может цифровой фильтр дискретного времени [* выход фильтра меняется ступенчато с приходом нового тактового импульса, аналоговый сигнал меняется непрерывно <с точностью до заряда электрона >] . В данном случае - в формате взвешенного аналогового суммирования выходных битов последовательности ( нерекурсивная цифровая фильтрация - КИХ). Частота среза такого фильтра пропорциональна тактовой частоте [* частоте суммирования в фильтре ] . Кроме того, цифровой фильтр позволяет получить очень низкую частоту среза ( доли герца ), на которой аналоговые компоненты становятся слишком громоздкими.
Для того, чтобы получить взвешенную сумму последовательных бит требуется подключить параллельные линии сдвигового регистра через резисторы нужного номинала к суммирующей точке операционного усилителя. Для ФНЧ весовые коэффициенты должны быть пропорциональны значениям функции \( (\sin x)/x \) . Отметим, что некоторые разряды придётся инвертировать, потому что весовые коэффициенты могут иметь любой знак. Т.к. в схеме нет конденсаторов, выходной сигнал является простой суммой входных напряжений.
Приближение к гауссовому распределению улучшается по мере увеличения числа суммируемых разрядов. Дополнительным плюсом является сглаживание формы выходного сигнала. По этой причине желательно использовать столько разрядов сдвигового регистра, сколько возможно, добавляя нужное количество дополнительных секции регистра уже после линий обратных связей. Как и ранее, чтобы получить нужное входное напряжение, надо использовать подтягивающие резисторы или твердотельные ключи. Для такой задачи идеальна КМОП логика, имеющая в качестве рабочих уровней точные потенциалы земли и питания.
==980
Устройство на рис. 13.119 построено по описанной схеме и создаёт псевдослучайный аналоговый шум с полосой, которая меняется в очень широких пределах. Сигнал с генератора 2.0 MHz идёт на 24-разрядный программируемый делитель ’14536, на выходе которого получается набор частот от 0.12 Hz до 1 MHz , соответствующих двоичным коэффициентам деления. Сдвиговый регистр длиной 32 бита включён с отводами от 31 и 18 разрядов и создаёт последовательность максимальной длины с двумя миллиардами состояний ( полный цикл при максимальной тактовой частоте составляет один час). В примере используется взвешенное суммирование 32 последовательных значений функции \( (\sin x)/x \) . Операционные усилители \(U_{1a}\) и \(U_{1b}\) масштабируют прямые и инверсные элементы суммы соответственно, а итоговый сигнал формируется на \(U_2\) . Усиление подобрано таким образом, чтобы получить сигнал без постоянной составляющей амплитудой 1.0 Vrms на нагрузке 50 Ω ( или 2.0 Vrms без нагрузки ). Отметим, что указанные напряжения не зависят от тактовой частоты, т.е. рабочей полосы. Частота среза цифрового фильтра составляет 0.05 \( f_{clock} \) , что позволяет получить белый шум в 24 диапазонах в полосе до 50 kHz ( на максимальной частоте ) и вплоть до 0.006 Hz ( на минимальной ). Схема имеет и нефильтрованный выход ±1V .
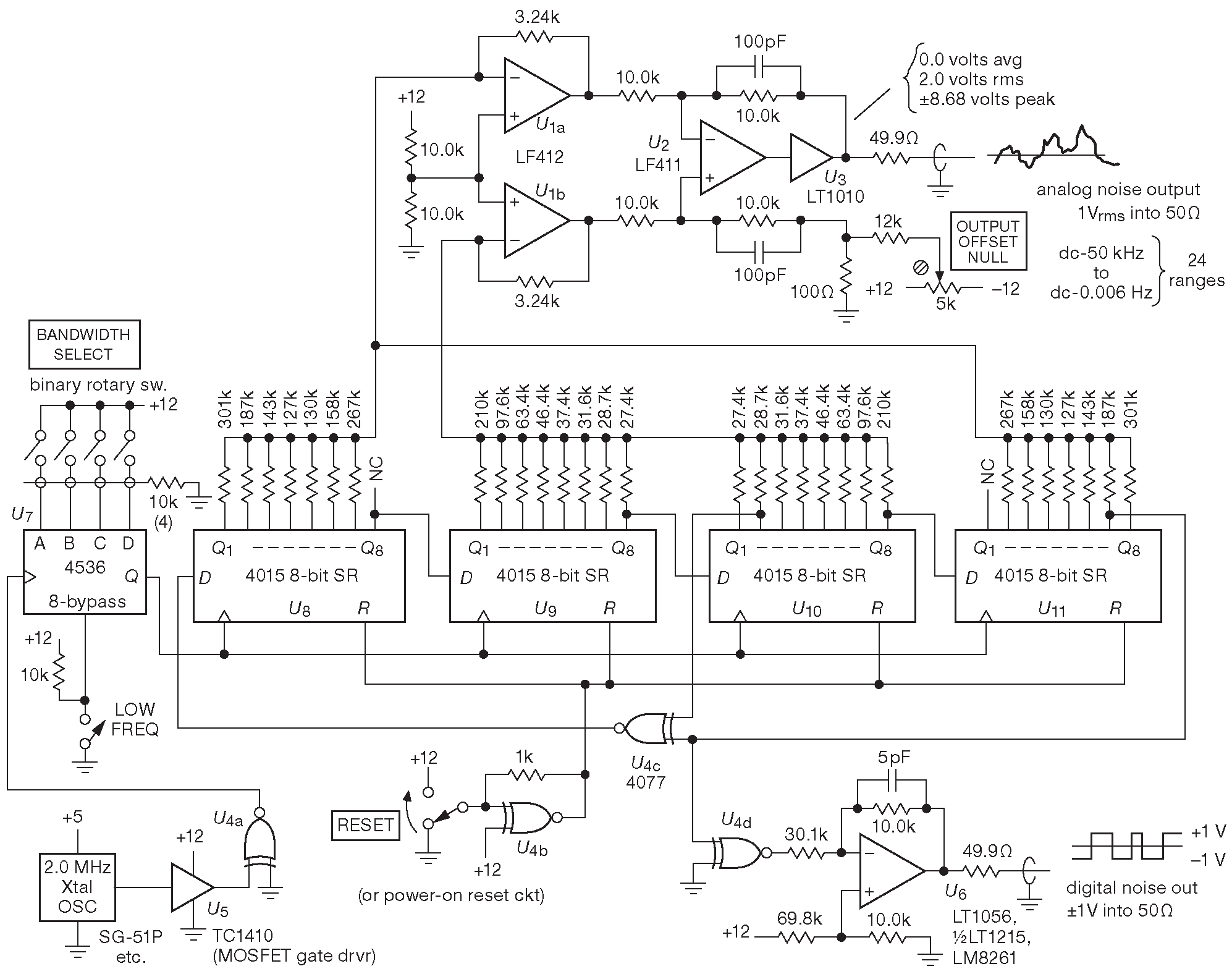
Рис. 13.119 Лабораторный источник псевдослучайного шума с широким диапазоном рабочих частот. Идея позаимствована у генератора 3722A фирмы Hewlett Packard ( «прецизионного цифрового прибора» в терминологии образца 1967 года ). Если требуется увеличить рабочую полосу шума, оставаясь в рамках дискретной логики, можно использовать регистры 74LV164A, которые гарантируют рабочую частоту 125 MHz при 5V . Аналоговая часть схемы потребует соответствующих изменений. Либо можно взять cPLD или FPGA ( §11.3.3 ), но, коли дело зашло так далеко, возможно, правильнее будет реализовать цифровой ФНЧ на процессоре цифровой обработки сигнала. Следующий шаг - реализовать всю цифровую часть на быстром микроконтроллере ( §11.3.5 и Часть 15 ) и использовать для генерации шума встроенный ЦАП. [* Сравните с математической моделью цифрового фильтра 6.48 ]
==981
Схема имеет несколько интересных особенностей. В качестве элемента обратной связи используется вентиль «ИСКЛЮЧАЮЩЕЕ-ИЛИ» с инверсией, что позволяет инициализировать регистр простым сбросом. В таком включении выбрасывается недопустимая комбинация «все единицы», в отличии от обратной связи на обычном «ИСКЛЮЧАЮЩЕМ-ИЛИ», где недопустимы «все нули». Все остальные свойства псевдослучайной последовательности сохраняются.
Взвешенная сумма конечного числа элементов не может создать настоящее гауссово распределение шумовых амплитуд, потому что их максимальная величина ограничена [*конечностью суммы ] . В данном примере расчёт даёт +4.34 V на нагрузке 50 Ω , т.е. пик-фактор равен 4.34 . Это достаточно важная величина, потому что усиление \(U_1\) и \(U_2\) должно выбирать так, чтобы исключить ограничение в выходном каскаде. И, наконец, интересен метод получения выходного сигнала с нулевым синфазным напряжением из логических уровней КМОП ( НИЗКИЙ = 0V , ВЫСОКИЙ = 12.0 V ).
13.14.6 Несколько напутственных замечаний
Несколько замечаний о последовательностях на сдвиговых регистрах в качестве источника аналогового шума 138 . Есть соблазн посчитать такой метод ( с учётом его фундаментальных свойств ) «достаточно случайным» при заданном числе прогонов, в течении какого-либо времени и т.п. ограничениях. Но надо понимать, что настоящий автомат, бросающий монетки не выкидывает равное число нулей и единиц, а его коэффициент автокорреляции не является абсолютно плоским для последовательности конечной длины. Можно выразить мысль иначе. Если использовать выходную псевдослучайную последовательность для управления движением объекта ( 1 = шаг вперёд, 0 = шаг назад ), то после прохождения полного цикла последовательности движение завершится в точке, отстоящей на один шаг от начального положения. Вряд ли данный результат можно считать и в самом деле случайным.
Изложенная только что мысль о неидеальных свойствах псевдослучайных последовательностей работает только если последовательность рассматривается как единое целое - все 2n–1 битов. Если речь идёт о какой-либо её части, то степень случайности вполне сравнима с таковой у автомата для подбрасывания монет. Можно привести такую аналогию. Ситуация напоминает случайное вынимание из урны шаров общим числом K , примерно поровну красных и синих. Если брать шары и не возвращать их обратно, то поначалу можно ожидать близкого к случайному результата, но по мере опустошения урны результат станет всё сильнее зависеть от исходного соотношения цветов.
И вновь, на вопрос можно взглянуть как на случайное перемещение. Если условиться, что единственным неслучайным свойством сдвигаемой последовательности является точное равенство числа нулей и единиц ( забудем о лишней единице ), можно показать, что при случайном перемещении взад-вперёд можно удалиться от исходной точки на \[ X=\sqrt{\frac{r(K-r )}{(K-1 )}} \] после r выборок из общего числа из K/2 нулей и K/2 единиц. При по-настоящему случайном перемещении X равно \(\sqrt r\) , а множитель ( K–r )/( K–1 ) отражает конечность содержимого урны. До тех пор пока r ≪ K , степень случайности перемещения почти не меняется по сравнению с чисто случайным ( когда урна бездонная ). В таком случае отличить псевдослучайный генератор от истинно случайного невозможно.
Конечно, успешное прохождение данного теста не означает, что будут пройдены и другие испытания на случайность, например, такие как степень корреляции более высокого порядка. Она влияет на характер фильтрации аналогового шума. Дело в том, что хотя распределение амплитуд создаваемого шума приближается к гауссовому, его амплитудные характеристики более высокого порядка отличаются от таковых у чисто случайных процессов. Считается, что использование большего числа обратных связей ( предпочтительным является возможно более близкое к m/2 значение ) с использованием древовидной схемы включения элементов «ИСКЛЮЧАЮЩЕЕ-ИЛИ» создаёт более «качественный» в этом отношении псевдослучайный шум.
Разработчикам генераторов шума следует познакомиться со сдвиговым регистром переменной длины ’4557. Он имеет шесть входов управляющих длиной, которые позволяют выставить любое значение от 1 до 64 шагов. ’4557 удобно использовать в связке с ’4015 или ’164, чтобы получить отвод в n-ной позиции. Другой удобной микросхемой является ’HC(T)7731 - счетверённый 64-разрядный сдвиговый регистр ( всего 256 битов ), который может работать на частоте до 30 MHz (min). Ещё удобнее и проще создавать PRBS с помощью программируемой логики ( cPLD и FPGA, см. Часть 11 ). Задачу могут решать и микроконтроллеры, но PLD работают быстрее 139 .
==982
Если нужна очень высокая скорость, можно возвратиться к старой доброй дискретной логике, как это сделано в «программируемом тактовом генераторе» CG635 фирмы Stanford Research Systems 140 , который может выдавать 7-шаговые PRBS ( 27–1 ) на частоте 1.55 GHz 141 . Делается это с использованием некоторых изящных трюков.
- В качестве толпы триггеров взяты представители дифференциальной эмиттерно-связанной логики MC100EP52D. Это быстрый D-триггер имеет время установки 0.05 ns , нулевое время удержания и 0.33 ns (тип.) время распространения.
- Они используют тихие и быстрые дифференциальные линии данных и тактовый сигнал.
- Узкое место - время распространения в элементе «ИСКЛЮЧАЮЩЕЕ-ИЛИ» - 0.3 ns , поэтому
- цепочка триггеров закольцована, причём линия данных идёт по часовой стрелке, а линия тактирования - против часовой. Такое включение даёт для первого триггера задержку тактового сигнала относительно двух последних порядка 0.25 ns , что позволяет учесть время установки данных от элемента «ИСКЛЮЧАЮЩЕЕ-ИЛИ».
Описанная геометрия платы вызывает задержку тактового сигнала между триггерами порядка 0.05 ns , позволяя красиво решить непростую задачу разводки тактового сигнала. Результат работы можно видеть на рис. 13.120 .
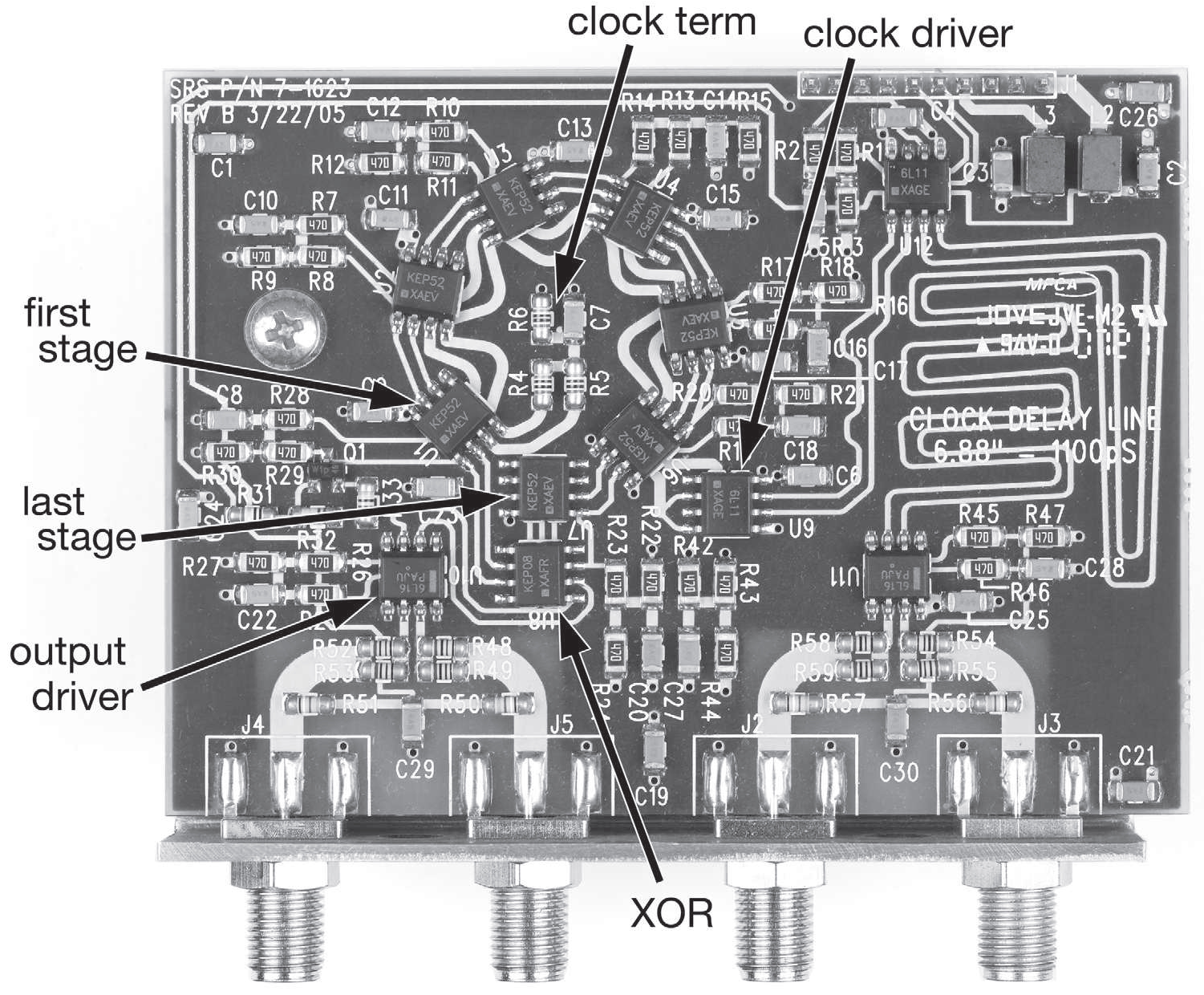
Рис. 13.120 Топология платы в виде беговой дорожки для быстрого ( до 1.55 Gbps ) 7-разрядного генератора псевдослучайной последовательности, собранного на LVPECL элементах серии 100EP. Данные идут по часовой стрелке, а тактовые импульсы - против, и всё работает
13.14.7 Генератор «настоящего» случайного шума
Ранее сообщалось, что алгоритмические методы создания «шума» не дают по-настоящему случайный результат: зная алгоритм можно предсказать, как будет выглядеть последовательность. На эту тему написаны горы книг 142 , и все они сообщают простую мысль: если требуется случайный шум, необходим иной метод.
Хорошей начальной точкой будет какой-либо физический процесс ( типа радиоактивного распада ), который случаен по самой природе и, естественно, непредсказуем. Есть и другие физические процессы, которые дают столь же хороший результат. Например, шум лавинного пробоя в полупроводнике. Схема, работающая по такому принципу, использовалась для набора блока случайных данных, который Numerical Recipes продаёт на CD-диске через Amazon. Схема приведена на рис. 13.121 . Описание увековечено на диске вместе с ~250MB того, что автор Вильям Пресс скромно обозначил как «самые лучшие “случайные” биты из всех возможных» :
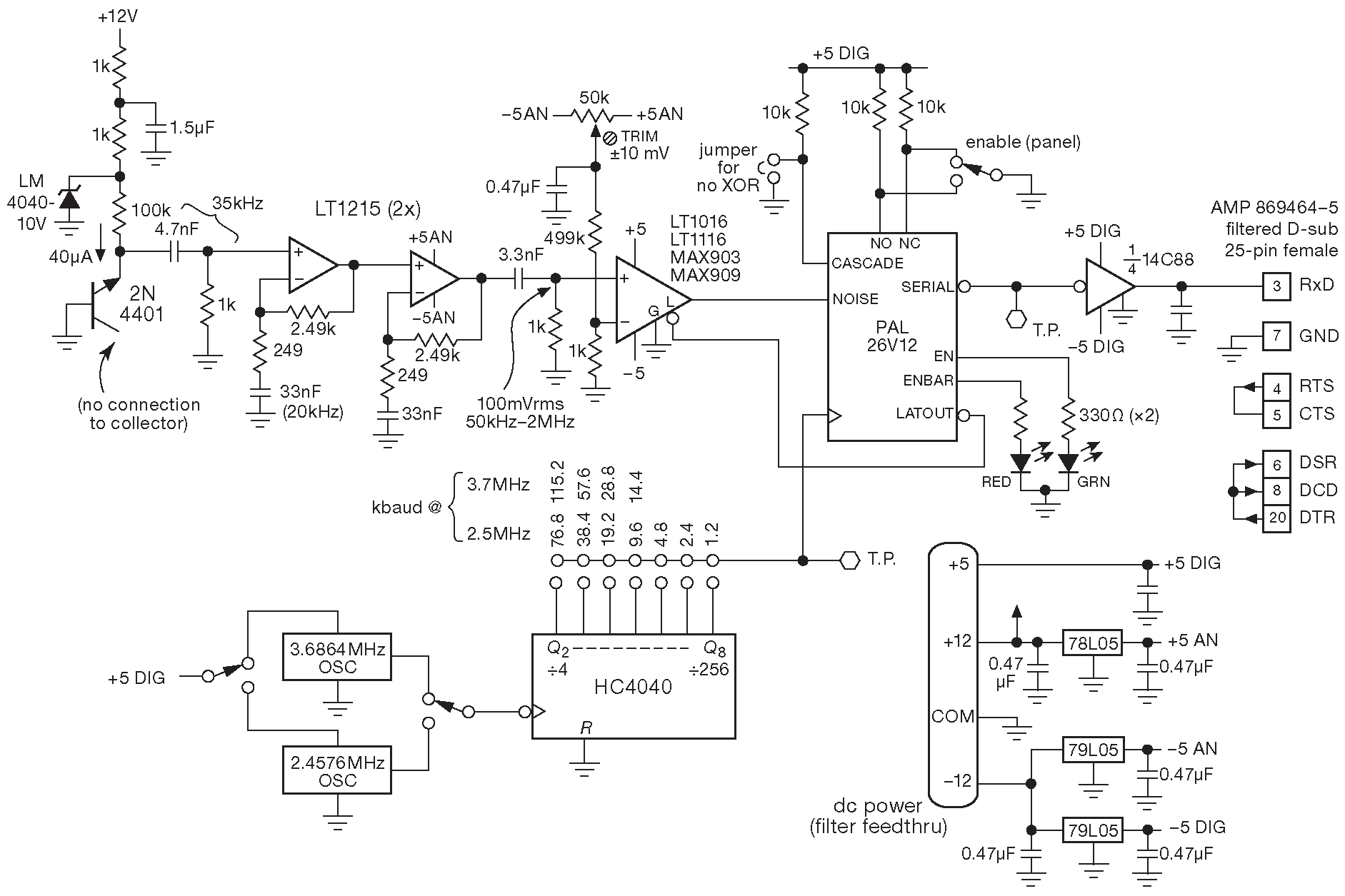
Рис. 13.121 Использование физического процесса (явления лавинного пробоя в полупроводнике ) для создания случайных данных
«Профессор Пол Хоровиц и Гарвардского Университета был столь любезен, что собрал для нас электронный источник физически случайных данных. Aналоговым источником служит полупроводниковый переход транзистора, который работает в качестве диода с лавинным пробоем. Шумовой ( тепловой ) ток создаётся в ходе случайного образования электронно-дырочных пар, обусловленного квантово-механическими процессами в переходе. Выходной сигнал с устройства, проверенный анализатором спектра, плоский от постоянного тока и до 50 MHz.Прибор ( рис. 13.121 ) усиливает аналоговое напряжение на переходе и считывает его на скорости в восемь раз большей, чем частота считывания данных ( её можно выбрать в диапазоне от 1.2 до 115.2 килобод ). Время считывания напряжения ( «апертура» ) очень мала и для стробируемого компаратора LT1016 составляет порядка 2 ns, позволяя при необходимости увеличить скорость выдачи данных. Положительному напряжению соответствует «1», отрицательному - «0». Полученные биты задвигаются в регистр. Каждые восемь бит выводятся в виде непрерывного потока байтов в последовательный канал. Вся цифровая часть схемы выполнена на микросхеме программируемой логики PAL 26V12. Её прошивка прилагается.
Никаких дополнительных действий по обработке получаемых данных ( смешивание, скремблирование, шифрование и т.д. ) не проводится намеренно, чтобы можно было измерять степень случайности исходного источника. Схема имеет некоторый поддающийся измерению уровень неслучайности: число нулей отличается от числа единиц в пятом знаке. Уровень неслучайности можно подстраивать потенциометром. Отметим, что для одного уверенного измерения такого смещения требуется накопить порядка 108 бит, но авторам было достаточно того, что асимметрия имеется. Смещение слегка меняется со временем, предположительно отражая изменения температуры и прочих условий работы устройства.
При анализе накопленных цифровых данных не удалось обнаружить следов неслучайности более высокого порядка. В частности не удалось найти никаких признаков неслучайности второго порядка или автокорреляции для небольших задержек. Отсутствует неравномерность спектра на 60 Hz и нескольких первых гармониках. Физические основы схемотехники предполагают, что для M-точечной статистики, где M>2, исключая случай многоточечных данных, полученных в результате медленного дрейфа одного значения, степень неслучайности падает с ростом M. Основанием для такого утверждения служит отсутствие в полупроводнике механизмов «памяти», а длительность происходящих в нём процессов как минимум на порядок короче, чем рабочая полоса 50 MHz.
Таким образом, даже в те моменты, когда выход схемы демонстративно неслучаен, можно считать, что уровень энтропии, приходящейся на один бит, очевидно, близок к 1 ( совершенно случайному значению ). Если ( 1–ε ) обозначает энтропию, приходящуюся на один бит ( для большого числа битов ), тогда можно считать, что с высокой степенью экспериментальной достоверности можно считать, что ε<0.01 ( получить математическое доказательство этого утверждения не представляется возможным ). К слову сказать, необработанные данные со схемы легко проходят все тесты из набора “Marsaglia’s Diehard battery of tests”.»
==983
Возвратимся к содержимому CD-диска. Выходные данные с описанного устройства были только начальной точкой ( «фазой сбора» ) для сложной последовательности операций, заканчивающейся их публикацией. «Фаза улучшения» состояла из трёх прогонов данных через шифрование с помощью DES алгоритма с проведением операции «ИСКЛЮЧАЮЩЕЕ-ИЛИ» со свежими данными между циклами шифрования и по его окончании. Описание полной процедуры можно найти на диске в каталоге «Museum».
13.14.8 «Гибридный цифровой фильтр»
Пример на рис. 13.119 возвращает к интересной теме - цифровой фильтрации, обсуждавшейся в §6.3.7 . Речь идёт о простом 32-стадийном фильтре низких частот с конечной импульсной характеристикой ( КИХ) . В генераторе шума он выполнен по гибридной технологии. Выборки цифровые ( логические ВЫСОКИЕ или НИЗКИЕ уровни с 32 выходов сдвигового регистра на \(U_8-U_{11}\) ) , но взвешенная сумма получается как аналоговое суммирование токов от двух операционных усилителей ( \(U_{1ab}\) ) в общей точке. Обычно цифровой фильтр работает с данными, получаемыми при дискретизации аналогового сигнала. Каждый элемент данных представляет собой многобитное значение ( например, для звукового CD речь идёт о 16-разрядных числах ) и поступает со скоростью, достаточной для сохранения всего частотного диапазоне интересующего сигнала ( для звукового CD \( f_{samp} \) =44.1 kHz - на 10% выше, чем критический порог 2\( f_{max} \) ) . В таком случае взвешивание и суммирование можно выполнять чисто цифровыми методами на умножителях и сумматорах. Отметим, однако, что цифровая обработка сигнала не требует, чтобы исходное аналого-цифровое преобразование порождало многобитные слова. Ранее в этой части обсуждалось сигма-дельта преобразование ( §13.9 ), которое является отличной иллюстрацией «однобитового» цифрового потока, вполне пригодного для обработки цифровым фильтром.
==983
135 Этот же пример используется в Части 11 [* §11.3 ] для демонстрации возможностей программируемой логики. Там одна и та же PRBS схема реализуется на дискретной логике, на программируемой логике и на микроконтроллере. См. также использование битовых последовательностей для генерации аналогового шума §8.12.4.A . <-
136 Критерием максимальной длины является несократимость и простота порождающего полинома \(1+x^n+x^m\) в поле Галуа GF(2). <-
137 Логических вход с ограничителями и связью по переменному току похож на акулу: он или переключается, или умирает. <-
138 Авторы обязаны этими рассуждениями своему прежнему сослуживцу Эду Парселу ( Ed Purcell). <-
139 Ещё быстрее заказные микросхемы, если, конечно, есть лишние $50k. <-
140 Которая столь любезно прилагает полную схему и список компонентов к своим приборам. <-
141 Кроме того, для тестирования на уровень ошибок используются последовательности длиной \( 2^{23}-1\) и \( 2^{31}-1\) . <-
142 Например, Том 2 классического труда Дональда Кнута «Искусство программирования». <-

