2.5 Отрицательная обратная связь
==115
Ранее неоднократно заявлялось, что обратная связь является лекарством от всех проблем: и при задании рабочей точки усилителя с заземлённым эмиттером ( §2.3.4 и §2.3.5 ), и использовании дифференциального усилителя с токовым зеркалом в качестве активной нагрузки ( §2.3.8.C ), и минимизации переходных искажений в симметричном эмиттерном повторителе ( §2.4.1.A ). Но она на самом деле ещё лучше. Отрицательная обратная связь - совершенно замечательный метод исправления любых недостатков: искажений и нелинейностей, частотной характеристики усиления, отклонения от идеала параметров источников тока и напряжения и вообще всего на свете.
==116
Полностью возможности обратной связи будут раскрыты в Части _4 , где рассказывается об универсальном аналоговом компоненте - операционном усилителе ( «ОУ» ), чьё функционирование немыслимо без обратной связи. Но теоретические основы её организации будут пояснены уже здесь, частью потому что она широко используется в транзисторных схемах, частью потому что встретилась уже в усилителе с эмиттерной дегенерацией, линейность которого была существенно улучшена обратной связью по сравнению со схемой усилителя с заземлённым эмиттером.
2.5.1 Введение в обратную связь
Обратная связь столь широко вошла в жизнь, что термин прочно закрепился в языке. В системах управления обратная связь сравнивает текущее состояние конкретного параметра с его желательной величиной с последующим изменением корректирующего воздействия. В качестве «системы управления» может выступать что угодно. Это может быть движущийся по дороге автомобиль, в качестве параметров выступать положение и скорость, а корректирующее воздействие идёт через рулевое колесо, педаль газа и тормоз. В усилителе может идти речь об увеличении входного сигнала, поэтому обратная связь сравнивает входной сигнал с частью выходного.
В усилителях отрицательная обратная связь просто заводится обратно на вход так, чтобы компенсировать часть входного сигнала. Это может показаться довольно глупым занятием, результатом коего будет простое снижение усиления. Гарольд Блэк (Harold S. Black ), который попытался запатентовать обратную связь в 1928 году, получил именно такой отзыв. По его словам патентное ведомство сравнило заявку с изобретением вечного двигателя 62 . Отрицательная обратная связь и в самом деле снижает усиление, но взамен улучшает другие характеристики, освобождает схему от искажений и нелинейности, выравнивает частотную характеристику ( или подгоняет её под данный частотный диапазон и профиль ) и увеличивает предсказуемость всех параметров. Чем глубже отрицательная обратная связь, тем меньше характеристики всей схемы зависят от величины исходного усиления ( без обратной связи ) и тем больше от характеристик самой цепи обратной связи. Операционные усилители ( дифференциальные усилители с очень большим коэффициентом передачи, см. Часть _4 ) практически всегда эксплуатируются с ограничением усиления, заданным обратной связью. Исходные цифры с разомкнутой петлёй ( без обратной связи ) достигают миллиона и более.
Цепь обратной связи может быть частотно или амплитудно-зависимой, задавая АЧХ сложной или нелинейной формы. Типичный пример последней - логарифмический усилитель. Он строится с использованием нелинейного элемента в обратной связи - диода или транзистора, имеющего логарифмическую зависимость \( V_{BE}\) от \(I_C\) . Обратная связь может формировать источник тока ( близкий к бесконечному выходной импеданс) или источника напряжения ( близкий к нулевому выходной импеданс), либо влиять сходным образом на входное сопротивление. В общем случае, тот параметр, который используется для организации обратной связи, и оказывается улучшен в ходе её работы. Таким образом, используя для обратной связи выходной ток, получают хороший источник тока 63 .
Разберём, как обратная связь работает и как влияет на работу усилителя. В ходе разбора будут выведены простые формулы входного и выходного импеданса и усиления схемы с отрицательной обратной связью.
2.5.2 Соотношения для усиления
Рассмотрим рис. 2.85A . Там изображён уже знакомый каскад с общим эмиттером и эмиттерной дегенерацией. Если рассматривать транзистор с точки зрения уравнения Эберса-Молла, малое изменение напряжения база-эмиттер ( \(Δ V_{BE}\) ) задаёт изменение тока коллектора. Но \(Δ V_{BE}\) меньше, чем входное напряжение \( V_{in}\) из-за падения на резисторе \(R_E\) . Если нагрузки на выходе нет, то соотношение для \(Δ V_{BE}\) имеет приведённый на рисунке вид. Т.е. каскад с эмиттерной дегенерацией - то же самое, что и усилитель с заземлённым эмиттером, охваченный обратной связью. [* См. §X2.4.1 ] .
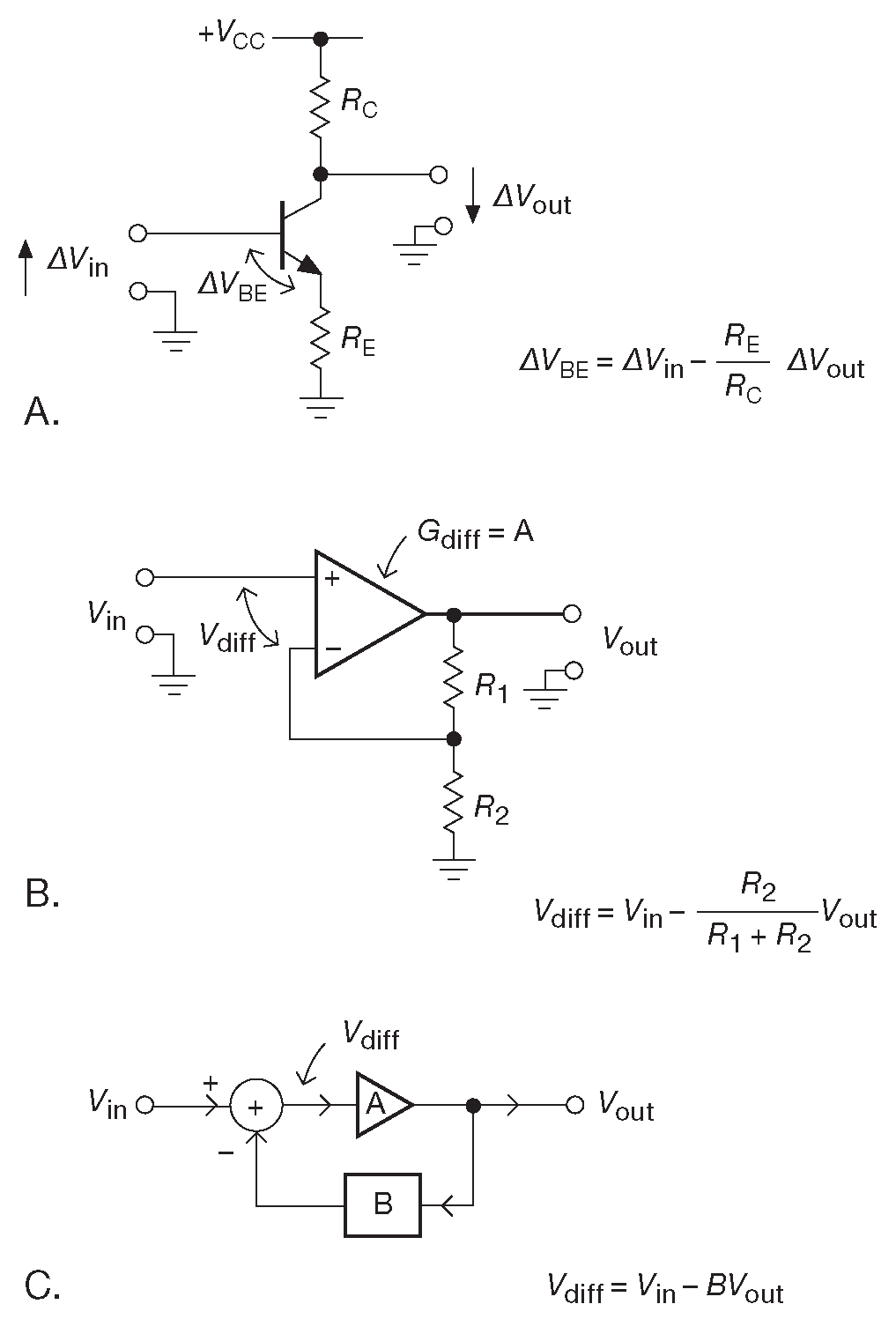
Рис. 2.85 Отрицательная обратная связь вычитает из входа часть выходного сигнала. (A) Каскад с общим эмиттером. (B) Дифференциальный каскад, включённый по схеме неинвертирующего усилителя. (C) Блок-схема передаточного звена с обратной связью
Схема имеет несколько особенностей, которые будут рассмотрены в более явном виде на рис. 2.85B . Здесь изображён дифференциальный каскад с усилением G=A для разностного сигнала. Часть выходного сигнала вычитается из входного \(v_{in}\) . Она находится из формулы простого делителя, как показано на рисунке. Это очень распространённая схема, широко используемая при включении операционных усилителей ( Часть _4 ) и называемая «неинвертирующий усилитель».
==117
При обсуждении обратной связи общепринятой практикой является использование блок-схемы передаточного звена, подобного изображённому на рис. 2.85C . Здесь коэффициент обратной связи обозначен символом B . Такой вариант удобнее, потому что имеет более общий вид ( обратная связь может иметь частотно зависимые компоненты, например, конденсаторы и нелинейные элементы, например, диоды ). Кроме того, такая форма упрощает соотношения. Для делителя \( B=R_2/( R_1+R_2 ) \) .
Выведем формулу для коэффициента передачи. Исходная схема имеет усиление без обратной связи A . Цепь обратной связи вычитает часть B выходного напряжения из входного сигнала ( позднее соотношения будут переписаны в общей форме, в которую можно подставлять и ток и напряжение ). На вход усилительного звена поступает сигнал \( V_{in}-BV_{out}\) , но выход в A раз больше входа, значит: \( V_{out}=A( V_{in} - BV_{out}) \) или \[ V_{out}=V_{in}\frac{A}{1+AB}. \] Отсюда усиление с обратной связью равно \[ G=\frac{V_{out}}{V_{in}}=\frac{A}{1+AB} \qquad \qquad [2.16] \]
Терминология . Стандартные обозначения для величин таковы: G - усиление с обратной связью, A - усиление без обратной связи, AB - петлевое усиление, (1+AB) - возвращаемая разница или «коэффициент снижения чувствительности» . Цепь обратной связи иногда называют «бета цепью» ( никакой связи с бетой транзистора или \(h_{fe}\) нет ) 64 .
2.5.3 Воздействие обратной связи на усилитель
Рассмотрим воздействие обратной связи. Наиболее важные из последствий - предсказуемость величины усиления ( и снижение искажений ), изменение входного и выходного импеданса.
2.5.3.A Предсказуемость усиления
Усиление по напряжению равно G=A/(1+AB) . Предполагая бесконечное усиление без обратной связи A 65 , получаем G=1/B . При конечном усилении A обратная связь уменьшает эффекты от изменения A ( от частоты, температуры, амплитуды и т.п. ). Пусть A зависит от частоты в соответствии с графиком 2.86 . Такая кривая, безусловно, соответствует всеобщему представлению о плохом усилителе, т.к. коэффициент передачи меняется по частоте более чем в 10 раз. Добавим обратную связь с коэффициентом B=0.1 ( здесь хорошо встанет простой делитель ). Усиление с обратной связью теперь меняется от 1000/[1+(1000×0.1 )] или 9.90 до 10'000/[1+(10'000×0.1 )] или 9.99 , т.е. менее 1% по всему частотному диапазону ! Если перевести цифры в аудио формат, исходный усилитель имеет неравномерность АЧХ ±10 dB , а усилитель с обратной связью ±0.04 dB . Исходную величину коэффициента передачи 1000 можно восстановить, включив три таких каскада последовательно.
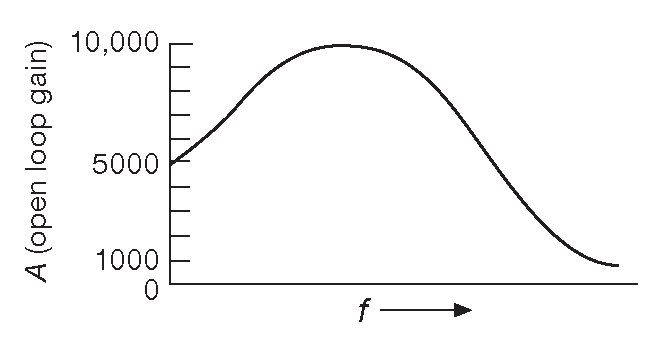
Рис. 2.86 Схема, чьё усиление A сильно меняется по частоте f
==118
Именно с этой целью и была исходно предложена обратная связь. Дело в том, что усилители для телефонных линий должны иметь очень малую неравномерность АЧХ. Вот как описывал своё изобретение автор Гарольд Блэк (Harold Black ) [ Elec. Eng., 53, 114, ( 1934 ) ].
«Построив схему, чьё усиление существенно, скажем, на 40 dB выше необходимого ( в 10'000 раз в энергетическом плане ), а затем подав выходной сигнал обратно на вход так, чтобы погасить избыточное усиление, можно обнаружить, что в результате чрезвычайно улучшилось постоянство уровня усиления, и почти полностью исчезла нелинейность».
Патент Блэка очень нагляден с десятками красивых иллюстраций, одна из которых воспроизведена на рис. 2.87 , для выразительности.
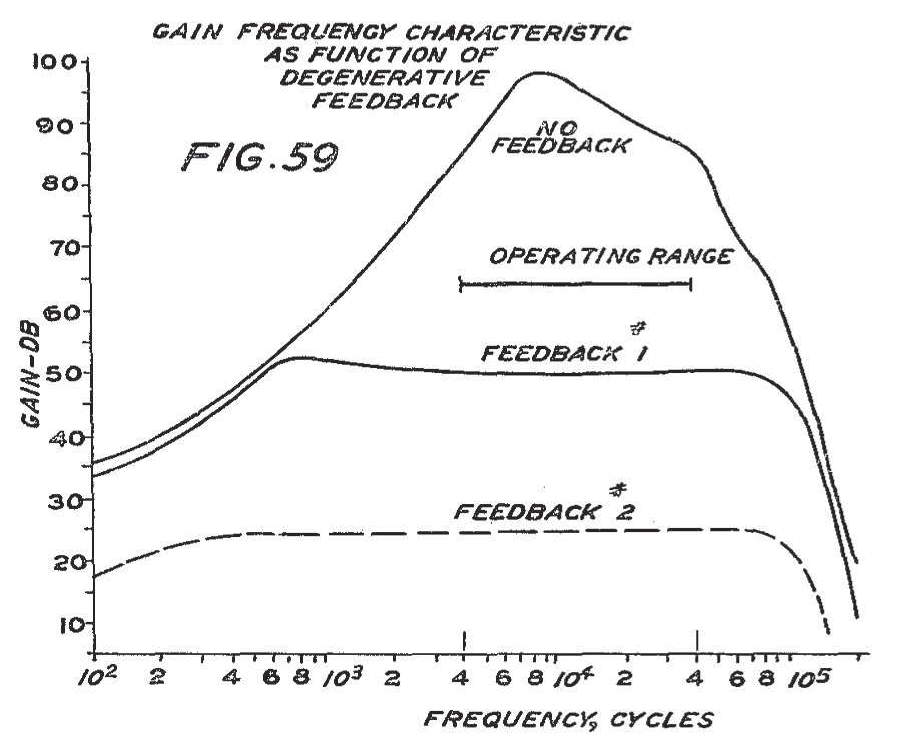
Рис. 2.87 Иллюстрация из патента Гарольда Блэка с ничего не говорящим именем «Система передачи сигналов»
Если взять частную производную G по усилению без обратной связи A ( т.е. \( ∂ G/ ∂ A\) ) , то станет видно, что относительное изменение усиления без обратной связи уменьшается за счёт снижения чувствительности : \[ \frac{ΔG}{G}=\left(\frac{1}{1+AB}\right )\left(\frac{ΔA}{A}\right ) \qquad \qquad [2.17] \]
Таким образом, для обеспечения хороших параметров, усиление в петле обратной связи AB должно быть много больше единицы. Перефразируя мысль, усиление без обратной связи должно быть существенно выше, чем усиление с обратной связью.
Очень важным следствием является снижение всех нелинейностей, которые являются простыми вариациями усиления, зависящими от амплитуды, ровно в той же пропорции.
2.5.3.B Входной импеданс
Обратная связь может быть организована так, чтобы вычитать из входа напряжение ( она называется последовательной обратной связью ) или ток ( параллельная обратная связь ). В рассмотренном выше неинвертирующем усилителе часть выходного напряжения вычиталась из входного дифференциального напряжения же, а схема 2.89B вычитает из входа ток . Воздействие на входной импеданс в обоих случаях прямо противоположное. Последовательная обратная связь увеличивает входной импеданс в ( 1+AB ) раз, а параллельная уменьшает его в той же пропорции. При бесконечном усилении исходной схемы входной импеданс для внешнего наблюдателя становится бесконечным или нулевым соответственно. Понимание облегчает тот факт, что последовательная обратная связь ( по напряжению ) вычитает напряжение из входного сигнала, уменьшая ( с коэффициентом AB ) изменение напряжения на сопротивлении входа [* т.е. снижает ток, а для внешней схемы события выглядят как увеличение входного импеданса ] . Это одна из форм вольтодобавки. А параллельная обратная связь ( токовая ) уменьшает входной сигнал, нагружая его дополнительным током.
Последовательная обратная связь ( со сложением напряжений )
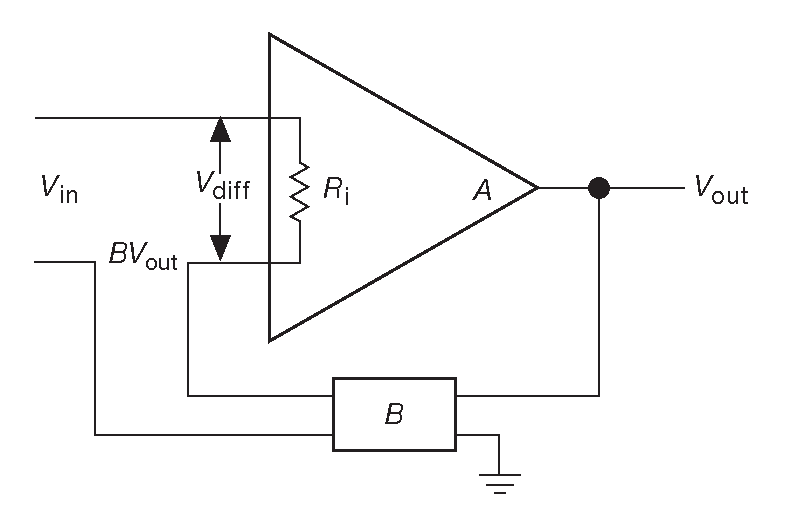
Рис. 2.88 Импеданс с последовательным включением обратной связи
Посмотрим, как действующее значение входного импеданса изменяется обратной связью. Рассматриваться будет только связь по напряжению, потому что вывод для обоих случаев будет аналогичным. Начнём с модели дифференциального каскада с некоторым входным сопротивлением ( рис. 2.88 ). Вход \( V_{in}\) уменьшается на величину \( BV_{out}\) , создавая дифференциальный сигнал \( V_{diff}=V_{in}-BV_{out}\) на входе усилителя. Входной ток позволит определить действующий входной импеданс. \[ I_{in}=\frac{V_{in}-BV_{out}}{R_i}=\frac{V_{in}\left(1-B\frac{A}{1+AB}\right )}{R_i}=\frac{V_{in}}{(1+AB )R_i}. \]
Входной импеданс \[ Z_{in} = \frac{V_{in}}{I_{in}} = (1 + AB )R_i. \]
==119
Другими словами, входной импеданс увеличивается с коэффициентом усиления в петле обратной связи плюс единица. Если использовать в схеме 2.85B дифференциальный каскад с естественным входным сопротивлением 100 kΩ и дифференциальным усилением \(10\space^4\) , а делитель поставить 99:1 (×100 ) , импеданс для входного сигнала составит примерно 10 MΩ , а коэффициент передачи с замкнутой петлёй обратной связи будет 99 66 .
Параллельная обратная связь ( со сложением токов )
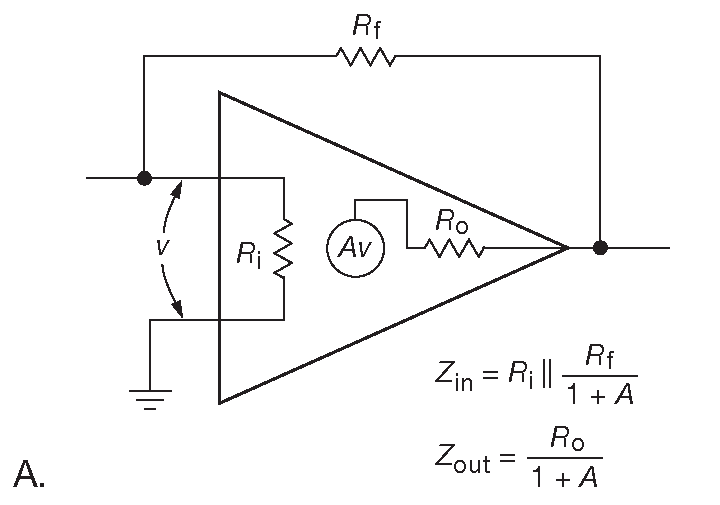
Рис. 2.89A Входной и выходной импеданс для трансрезистивного усилителя
Разберём рис. 2.89A . Импеданс со стороны входа усилителя напряжения с параллельной обратной связью ( по току ) уменьшается за счёт дополнительного тока с его выхода, который [* через цепь обратной связи ] противодействует изменению напряжения на входе 67 . Входной сигнал видит параллельное соединение
- усилителя с естественным входным сопротивлением \(R_i\) и
- сопротивления обратной связи \(R_f\) , поделенного в ( 1+A ) раз.
\[ Z_{in}=R_i∥\frac{R_f}{1+A} \]
[* Появление на входе напряжения сигнала вызывает появление на выходе усилителя потенциала такой величины и полярности, которое позволит через резистор обратной связи задавить входной сигнал в ноль. В результате внешний наблюдатель видит «две» параллельные нагрузки - входное сопротивление усилителя ( постоянное ) и «входное» сопротивление цепи обратной связи ( зависит от величины сигнала ), см. замечание на стр. 251 ] .
( Сможете ли вы доказать это? ) В варианте с очень большим усилением в петле обратной связи ( например, в схеме на ОУ ), входное сопротивление снижается до долей Ома. Это может показаться изрядным недостатком, но не стоит забывать, что речь идёт о преобразовании тока в напряжение ( «трансрезистивный усилитель» ), для которого низкий входной импеданс - хорошая характеристика. [* Низкий ( нулевой ) входной импеданс не образует делителя с выходным сопротивлением источника тока, т.е. не приводит к колебанию выходного напряжения источника, см. §1.2.3 ] . Примеры будут показаны в Части _4 , _8 и X4 .
Если добавить на вход резистор ( рис. 2.89B ), схема превращается в «инвертирующий усилитель». Его входное сопротивление описывается прилагаемыми к рисунку формулами. Схему можно рассматривать ( особенно для больших петлевых усилений ) как резистор на входе преобразователя ток-напряжение. В таком варианте \(R_{in}\) в пределе равно \(R_1\) , а усиление с замкнутой обратной связью составляет \(-R_2/R_1\) .
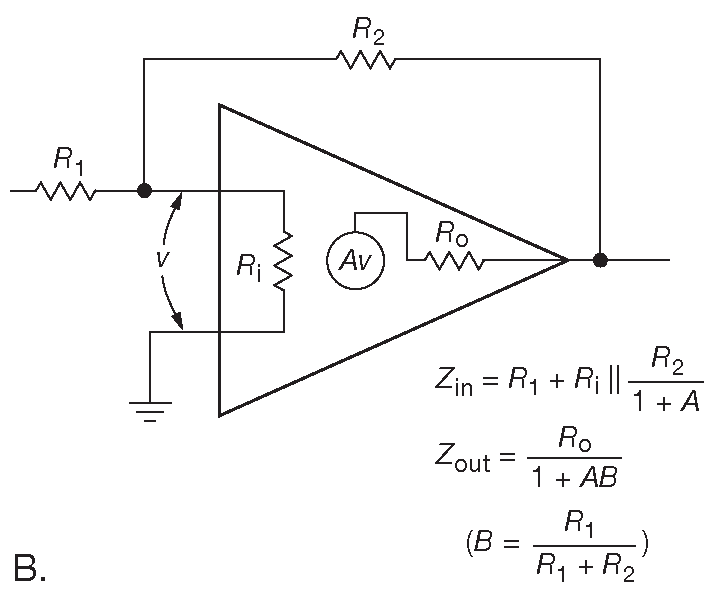
Рис. 2.89B Входной и выходной импеданс для инвертирующего усилителя
Очевиден и вывод формулы для коэффициента передачи инвертирующего усилителя, охваченного обратной связью с конечным усилением. \[ G = —A\frac{(1 — B )}{(1 + AB )} \quad , \]
где B , как и раньше, равно \(R_1/( R_1+R_2 ) \) . В случае большого усиления без обратной связи A получаем общий коэффициент передачи G=1–(1/B ) , т.е. G=\(-R_2/R_1\) .
Упражнение 2.20
Покажите вывод формул для входного импеданса и коэффициента передачи инвертирующего усилителя.
2.5.3.C Выходной импеданс
Здесь обратная связь оценивает выходное напряжение или выходной ток. В первом случае исходный импеданс без обратной связи будет уменьшен с коэффициентом ( 1+AB ), а во втором - увеличен во столько же раз. Проиллюстрируем эффект для случая обратной связи по напряжению.
==120
Теперь рассматриваем выходной импеданс ( рис. 2.90 ). На этот раз покажем импеданс в явной форме. Расчёты упрощаются следующим приёмом. Закоротим вход и подадим на выход напряжение \( V \) . По выходному току \(I\) можно получить выходной импеданс \(R_o'=V/I\) . Напряжение \( V \) на выходе создаёт на входе корректирующее воздействие –B\( V \) , которое в свою очередь усиливается внутренней схемой до A(–B\( V \) ). Тогда выходной ток: \[ I=\frac{V-A(-BV)}{R_o}=\frac{V(1+AB )}{R_o} \]
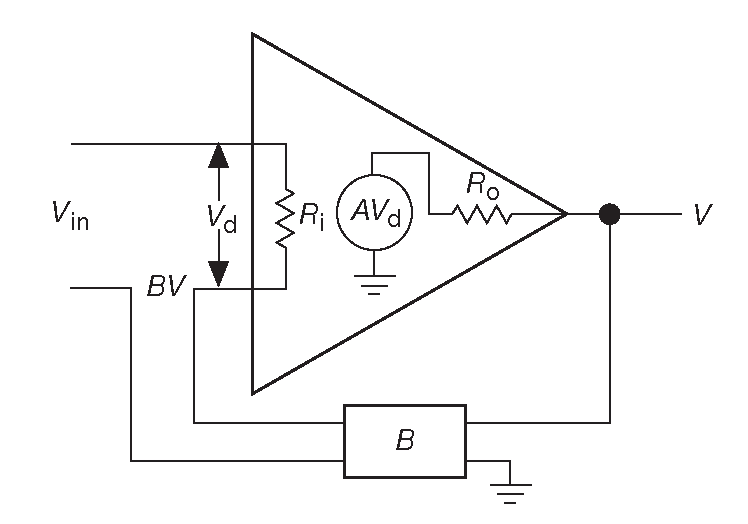
Рис. 2.90 Выходной импеданс
а действующий импеданс 68 составит \[ Z_{out}=\frac{V}{I}=\frac{R_o}{(1+AB )}. \]
2.5.3.D Обратная связь по току
Обратную связь можно использовать для оценки выходного тока . Уравнение для выходного импеданса примет вид \[ Z_{out}=R_o(1+AB ) \]
Можно иметь несколько ветвей обратной связи, каждая из которых может быть связью по напряжению или по току. В общем случае выходной импеданс определяется из соотношения Блэкмана 69 : \[ Z_{out}=R_o\frac{1+( AB )_{SC}}{1+( AB )_{OC}}, \] где \( ( AB )_{SC}\) - усиление в петле обратной связи, когда выход закорочен на землю, а \( ( AB )_{OC}\) - усиление в петле, когда выход разомкнут. Таким образом, обратная связь может использоваться для получения требуемого выходного импеданса. Для обычной ситуации использования одного вида обратной связи по напряжению или по току данное соотношение упрощается до предыдущих результатов. Продолжение дискуссии в Части X2 .
2.5.4 Две важные детали
Обратная связь - большая тема, которая сокращена здесь до простого обзора. Но есть две детали, о которых нельзя забывать даже на этом несколько поверхностном уровне знакомства.
2.5.4.A Нагрузка от цепи обратной связи
При расчётах обратной связи обычно предполагается, что бета-цепь не нагружает выход усилителя. Если это не так, то данный факт следует учитывать при расчёте усиления без обратной связи. Аналогично, если бета-цепь на входе схемы меняет усиление с разомкнутой обратной связью ( т.е. цепь подсоединена, но обратная связь разорвана ), то в расчётах нужно использовать изменившееся значение усиления. Наконец, все уравнения предполагают, что бета-цепь однонаправленная и не передаёт сигнал со входа на выход.
2.5.4.B Сдвиг фазы, устойчивость и «коррекция»
Основным элементом выражений для коэффициента передачи с замкнутой петлёй и соответствующего входного и выходного импеданса является усиление без обратной связи A . По умолчанию предполагается, что A - действительное число, т.е., что выходной сигнал совпадает по фазе со входным. В реальной жизни всё сложнее 70 . Причиной тому - имеющиеся в схеме емкости, эффект Миллера ( §2.4.5 ) и конечная рабочая полоса ( \( f_T \) ) активных компонентов. Под воздействием перечисленных факторов выход усилителя начинает отставать по фазе, причём по мере роста частоты отставание растёт. Данный факт имеет несколько следствий.
- Устойчивость
- Если отставание фазы в усилителе без обратной связи достигнет 180° , то отрицательная обратная связь станет положительной с возможным появлением колебаний. Вряд ли это нужно разработчику. (На всякий случай: условием возникновения колебаний является сдвиг фазы на 180° на частоте, при которой усиление в петле обратной связи AB равно единице ). Это серьёзное осложнение, особенно для схем с большим усилением ( как, например, в ОУ ). Проблема усугубляется, если цепь обратной связи добавляет сдвиг фаз, что является частой ситуацией. Именно с данным явлением идёт борьба при частотной коррекции усилителей, описанной в §4.9 .
- Усиление и сдвиг фаз
- В уравнении для коэффициента передачи с замкнутой обратной связью, а также входного и выходного импеданса входит усиление без обратной связи A . Например, усилитель напряжения с последовательной обратной связью ( рис. 2.85B,C , 2.88 и 2.90 ) имеет коэффициент передачи с замкнутой обратной связью \( G_{CL}\)=A/(1+AB) . Предположим, что A=100 и B=0.1 для получения итоговой величины \( G_{CL}\)=10 . Если у усилителя нет сдвига фаз, то \( G_{CL}\)≈9.09 и тоже не имеет сдвига фаз. Если же усилитель имеет отставание фазы 90° , то A оказывается чисто мнимой величиной ( A=–100j ), а усиление с замкнутой обратной связью становится G=9.90-0.99j . Таким образом, модуль усиления \(|G_{CL}|\)=9.95 , а фаза отстаёт примерно на 6° . Другими словами, существенный ( полпути до генерации! ) сдвиг фазы без обратной связи по факту предпочтительнее, т.к. усиление с замкнутой петлёй всего на 0.5% ниже желаемого ( а для нулевого сдвига он ниже на 9% ). Оплачивается это удовольствие остаточным сдвигом фазы и, естественно, предпосылками для потери устойчивости.
==121
Как ни надуманно смотрится данный пример, он отражает реальное положение вещей. Типовой операционный усилитель имеет задержку фазы примерно на 90° почти на всей ширине рабочей полосы, но благодаря высокому исходному усилению итоговая схема с обратной связью имеет очень небольшой сдвиг фазы и точное значение коэффициента передачи, практически полностью определяемые цепью обратной связи. Тема продолжается в Части _4 ( §4.9 ).
Упражнение 2.21
Подтвердите правильность вывода уравнения для \( G_{CL}\) .
2.5.5 Два примера транзисторных усилителей с обратной связью
Рассмотрим пару конструкций транзисторных усилителей, чтобы разобраться, как обратная связь влияет на параметры. Анализ, возможно, покажется несколько сложным, читателю предлагается сосредоточиться 71 .
На рис. 2.91 показана законченная схема транзисторного усилителя, охваченного отрицательной обратной связью. Рассмотрим, как он работает.
2.5.5.A Законченная схема транзисторного усилителя
Эта конструкция проста, очевидна и достаточно удобна для анализа. \(Q_1\) и \(Q_2\) образуют дифференциальную пару, работающую на каскад с общим эмиттером на \(Q_3\) . \(R_6\) - коллекторная нагрузка для \(Q_3\) . На выходе стоит симметричный эмиттерный повторитель на \(Q_4Q_5\) . Выходное напряжение контролируется цепью обратной связи из делителя \(R_4R_5\) и конденсатора \( C_2\) . Последний добавлен, чтобы снизить усиление на постоянном токе до единицы для стабилизации рабочей точки. \(R_3\) устанавливает ток покоя дифференциальной пары. Обратная связь гарантирует, что в состоянии покоя на выходе будет нулевое напряжение, значит, ток покоя \(Q_3\) составляет 10 mA ( он определяется падением на \(R_6\) , которое чуть меньше, чем \( V_{EE}\) ) . Цепочка диодов переводит выходной повторитель в проводящее состояние ( §2.4.1.B ), в результате на \(R_7R_8\) появляется падение напряжения, равное падению на одном диоде, т.е. ток покоя равен 60 mA . Каскад, следовательно, работает в режиме «класс-AB», что полезно для снижения переходных искажений. Рассеиваемая в режиме покоя мощность равна 1W на каждый выходной транзистор.
==122
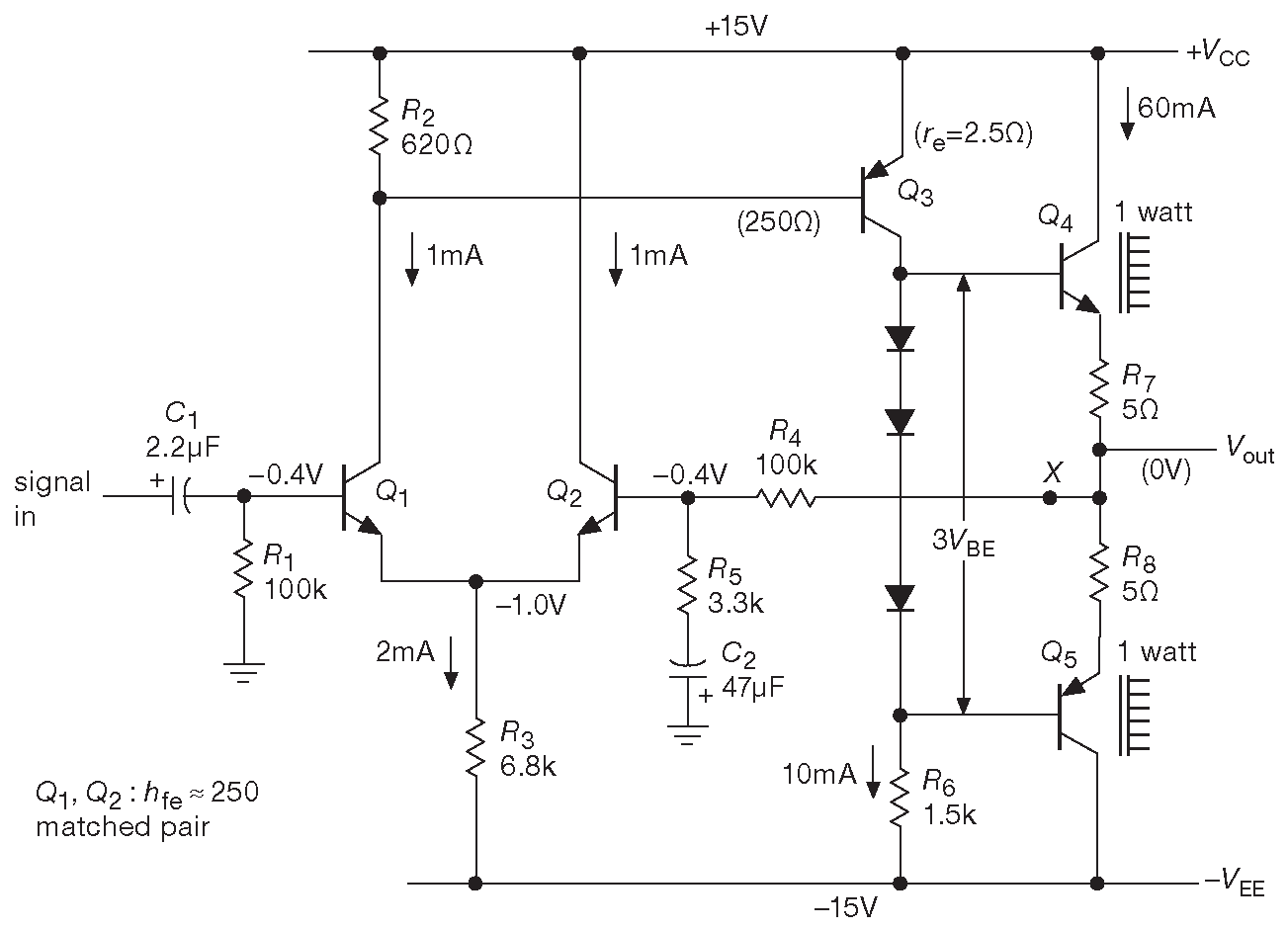
Рис. 2.91 Мощный транзисторный усилитель с отрицательной обратной связью
Единственным отличием от ранее рассмотренных схем является потенциал коллектора \(Q_1\) . В режиме покоя он равен \( V_{CC}\) минус одно падение на диоде. Такое смещение требуется для перевода \(Q_3\) в проводящее состояние, которое поддерживает обратная связь. Происходит это следующим образом. Если потенциал коллектора \(Q_1\) будет меняться в направлении земли, \(Q_3\) откроется больше, поднимая напряжение на выходе. [* \(Q_3\) открылся сильнее → увеличилось падение на \(R_6\) → базы \(Q_4\) и \(Q_5\) пошли вверх ( \(Q_5\) непосредственно, а \(Q_4\) через «проставку» из трёх диодов ) → \(Q_4\) чуть приоткрылся, \(Q_5\) - призакрылся ] . Это заставит \(Q_2\) сильнее проводить ток, сокращая ток эмиттера \(Q_1\) . Ток коллектора \(Q_1\) сократится, восстанавливая status quo. Номинал \(R_2\) выбирается так, чтобы ток покоя \(Q_1\) обеспечивал на нём одно падение на диоде [* рабочая точка \(Q_3\) ] . От этого потенциала зависит баланс токов через ветви дифференциальной пары [* через \(Q_3\) и цепь обратной связи ] в состоянии покоя. Данная схема имеет вполне заметный входной ток 4 μA , вызывающий падение 0.4 V на входном резисторе 100 kΩ . В транзисторных схемах, подобных этой, где входной ток заметно больше, чем в ОУ, очень важно поддерживать равенство сопротивлений на обоих входах. Возможно, входной каскад на парах Дарлингтона будет работать здесь лучше.
2.5.5.B Анализ
Проведём подробный анализ схемы и определим усиление, входной и выходной импеданс и уровень искажений. [* Враки, обошлись без искажений. Анализ искажений можно посмотреть в §X2.4 и в §2.3.4.A ] . Чтобы показать пользу обратной связи, подсчитаем все цифры и для замкнутой петли, и для разомкнутой, и выясним заодно, на что будет похожа рабочая точка в наихудшем случае ( без обратной связи ). Для оценки линеаризующего эффекта обратной связи усиление будет подсчитано для входного сигнала +10 V , –10 V и в состоянии покоя ( 0V ).
Разомкнутая петля ( Open loop)
- Входной импеданс
- Обрежем обратную связь в точке «X» и заземлим правый вывод \(R_4\) . Входной сигнал видит 100 kΩ в параллель с импедансом \(Q_1\) со стороны базы . Последний равен сумме удвоенного внутреннего сопротивления эмиттера \( r_e\) и импеданса, который видит эмиттер \(Q_2\) со стороны базы ( \(R_5/h_{fe}\) ) , умноженного на \(h_{fe}\) транзистора \(Q_1\) . Если принять \(h_{fe}\)≈250 , то \(Z_{in}\)≈250×[(2×25)+(3.3 kΩ/250)]≈16 kΩ .
[* Так, давайте разбираться.
• Зачем заземлили правый конец \(R_4?\)
Так мы обманываем цепь обратной связи, чтобы она думала, будто на выходе нулевое напряжение и вела себя тихо, но в схеме всеми своими импедансами и сдвигами фаз присутствовала.
• Как она может влиять, ведь на неё теперь не подаётся никакой сигнал \(?\)
Транзистору безразлично откуда приходит сигнал: из базы или с эмиттера. Дёрнешь за базу, изменится ток, дёрнешь за эмиттер, и тоже изменится ток. Т.е., если прямой сигнал с эмиттера \(Q_1\) изменил потенциал эмиттера \(Q_2\) ( или ток через переход база-эмиттер \(Q_2\) ), то потенциал базы \(Q_2\) изменится. Это эквивалентно приходу сигнала со стороны цепи обратной связи, и, соответственно, изменению в ней токов и напряжений. Вот вам и «не подаётся сигнал». Так работает дифференциальный каскад, каскОд, усилитель с общей базой, эмиттерная дегенерация и т.д. Сигнал на \(Q_2\) приходит с эмиттера ( прямой ) и с базы ( от обратной связи ) и оба влияют на его работу. Другими словами, цепь обратной связи влияет на поведение \(Q_2\) в той же степени, как и при нормальном включении. Нет только сигнала с выхода, и всё.
• Почему в расчётах участвует \(R_5\) , который изолирован от земли конденсатором \( C_2\) , но не участвует \(R_4\) , параллельный цепи \(R_5C_2\) , который уже сидит на земле ( куда был подключён в начале анализа схемы ) \(?\)
Потому что вход у нас развязан по постоянному току конденсатором \( C_1 \) , который на пару с \(R_1\) образует фильтр верхних частот со срезом ∼5 Hz ( \(τ\)=0.22 s ), а постоянная времени \(R_5C_2\) равна 0.15 s , т.е. почти такая же, и в полосе частот входного сигнала \(R_5\) отлично работает. Более того, импеданс \(Q_1\) со стороны базы включён параллельно с \(R_1\) , т.е. уменьшает номинал резистора в фильтре и сдвигает частоту вверх, гарантированно попадая в область, где \( C_2\) на схему не влияет ( короткозамкнутая цепь ). \(R_4\) в 30 раз больше \(R_5\) и уменьшает номинал последнего на 3% . Это ниочём.
• А почему ( \(h_{fe}\) ) , а не \(β ?\)
Потому что это пример ещё из первого издания ].
- Выходной импеданс
- Импеданс \(Q_3\) со стороны коллектора велик, поэтому импеданс источника для выходных транзисторов определяется величиной \(R_6\) ( 1.5 kΩ ). Выходной импеданс около 15 Ω ( \(β\)≈100 ) плюс 5 Ω сопротивление в эмиттере, итого 20 Ω . Внутренним сопротивлением эмиттера \( r_e\)=0.4 Ω можно пренебречь.
- Усиление
-
Входной дифференциальный каскад нагружен на параллельное соединение \(R_2\) с сопротивление \(Q_3\) со стороны базы. Ток покоя \(Q_3\) 10 mA , следовательно, внутреннее сопротивление эмиттера 2.5 Ω . Отсюда сопротивление со стороны базы 250 Ω ( \(β\)≈100 ). Тогда коэффициент передачи дифференциальной пары \[ \frac{250 Ω∥620 Ω}{2×25 Ω}=3.5 \]
Второй каскад - \(Q_3\) имеет усиление по напряжению 1.5 kΩ/2.5 Ω=600 . Общее усиление в рабочей точке равно 3.5×600=2100 . Коэффициент передачи \(Q_3\) существенно зависит от тока коллектора и меняется вместе с сигналом, т.е. нелинеен. Ниже его величина рассчитана для трёх уровней выходного напряжения.
Замкнутая петля ( Closed loop)
- Входной импеданс
- Схема использует последовательную обратную связь, поэтому выходной импеданс возрастает в ( 1+«усиление-в-петле» ) раз. Цепь обратной связи состоит из делителя с B=1/30 на частоте сигнала [*] . Поэтому общее петлевое усиление AB=2100/30=70 . Входной импеданс равен 70×16 kΩ в параллель со 100 kΩ , т.е. около 92 kΩ . Теперь входной импеданс определяется в основном резистором на входе.
- Выходной импеданс
- Схема использует обратную связь по напряжению [**] , значит, выходной импеданс снижается с коэффициентом ( 1+«усиление-в-петле» ) и составляет 0.3 Ω . Здесь следует отметить, что речь идёт об импедансе для малого сигнала, а не о том, что можно получить почти полный размах питания на нагрузке, скажем, 1 Ω . Размах выходного сигнала ограничивается резисторами в эмиттерах величиной 5 Ω , и на нагрузке 4 Ω можно получить не больше 10 Vpp .
- Усиление
- Усиление равно A/(1+AB) и в состоянии покоя равно 30.84 , если использовать точное значение для B . Чтобы оценить его стабильность с учётом обратной связи, было подсчитано усиление для трёх значений входного сигнала с обратной связью и без неё. Обратная связь, очевидно, серьёзно улучшает параметры схемы, но для корректности следует заметить, что усилитель можно было бы сделать с изначально более высокими параметрами, как-то: использовать эмиттерную дегенерацию и поставить в коллектор \(Q_3\) и в эмиттеры дифференциальной пары источники тока и т.д. Но в любом случае, обратная связь сильно улучшает ситуацию.
[*]
[* Определяется делителем \(R_4R_5\) . Постоянная времени \( ( R_4+R_5 )C_2\) составляет 4.7 s или ∼0.2 Hz . Ниже этой частоты начинается «постоянный ток»: \( C_2\) отключает \(R_5\) , делитель перестаёт работать, и остаётся один \(R_4\) ( т.е. коэффициент передачи 1:1 ), который следит за постоянным уровнем на выходе. Точка «–3db» лежит на частоте, на которой реактивное сопротивление \(C_2\) равно \(R_5\) ].
[**]
[* «По напряжению» значит, что присматривает за изменением выходного напряжения, которое через делитель \(R_4R_5\) подаётся на диффкаскад.
А можно по току \(?\)
Можно и по току. Для этого надо поставить токочувствительный резистор ( шунт ) на пути выходного тока и использовать падение на шунте как сигнал обратной связи. В итоге получится источник тока, управляемый напряжением, или транзистор \(!\)
Подсказка : в схеме уже есть \(R_7\) и \(R_8\). Дерзайте ].
[ amplifier could have been designed for better open-loop performance ]
loop) « 10k, Zout( closed loop) «500 Q, and G( closed loop) «9.5. ^out Open loop Closed loop -10 0 + 10 -10 0 +10 Zin 16k 16k 16k 92k 92k 92k Zout 20Q 20Q 20Q 0.3Q 0.3Q 0.3Q Gain 1360 2100 2400 30.60 30.84 30.90
2.5.5.C Пара с последовательной обратной связью ( Series-feedback )
На рис. 2.92 показана ещё одна транзисторная схема. [* По такой же схеме собран предусилитель фирмы Naim Audio, см. §8.5.5.A ] . Если рассматривать \(Q_1\) в качестве усилителя для напряжения база-эмиттер ( в контексте уравнения Эберса-Молла ), обратная связь берёт часть выходного напряжения и вычитает из входного сигнала [* меняет напряжение база-эмиттер со стороны эмиттера, а сигнал меняет его со стороны базы ] . Схема неочевидна, т.к. коллекторная нагрузка \(Q_2\) одновременно является частью цепи обратной связи [* см. §2.2.2.E где дан пример положительной обратной связи такого же вида на примере триггера Шмитта ] . Применяя показанный ранее метод, можно выяснить, что усиление для разомкнутой обратной связи A≈200 , усиление в петле AB≈20 , \(Z_{out}( OL ) \)≈10 kΩ , а с замкнутой петлёй \(Z_{out}( CL ) \)≈500 Ω , \( G_{CL}\)≈9.5 .
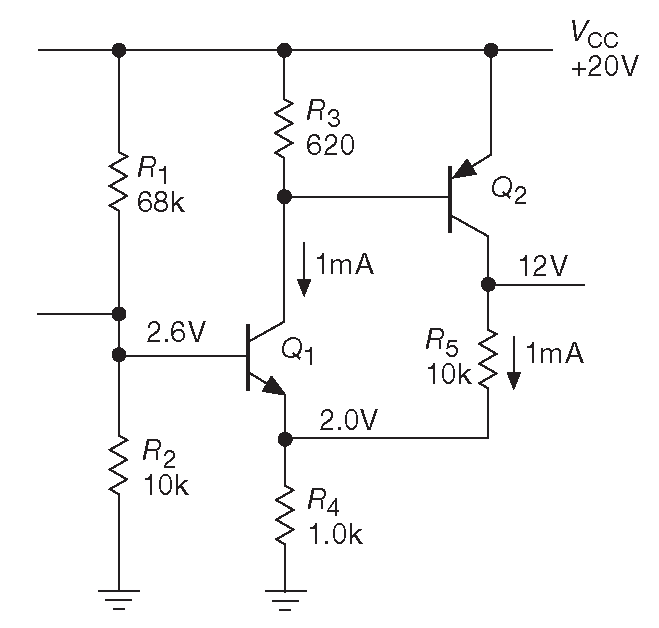
Рис. 2.92 Двухкаскадный усилитель с последовательной обратной связью
==123
Упражнение 2.22
Повторите расчёты
==123
62 См. отличную статью в IEEE Spectrum за декабрь 1977. Его патент не отрицательную обратную связь (#2,102,671 ), скромно названный «Система передачи сигналов», был выдан в 1937, через девять лет после подачи. <-
63 Обратная связь может быть и положительной : именно так работают генераторы. Несмотря на многообещающее название, данный вид обратной связи не так важен, как отрицательный вариант. Чаще это проблема, потому что цепь отрицательной обратной связи на какой-то частоте может набрать достаточно большой сдвиг фазы, который превратить её в положительную и вызовет самовозбуждение. Такое развитие событий оказывается неожиданно несложным делом, поэтому противодействие нежелательной генерации имеет специальное название - частотная коррекция . Данный вопрос кратко рассматривается в Части _4 ( §4.9 ). <-
64 Как будет видно дальше, усилитель с обратной связью имеет заметную задержку фазы со входа на выход. Поэтому усиление без обратной связи A правильнее выражать комплЕксными числами. Этот вопрос рассматривается в §2.5.4 . Пока будем использовать упрощённую форму, в которой выходное напряжение пропорционально входному. <-
65 Что неплохо соотносится с действительностью, т.к. типичное усиление ОУ без обратной связи составляет \( A_{OL} ≈ 10\space^6\) . <-
66 Конечно, зная, что усиление без обратной связи \(10\space^4\) , можно подкрутить отношение до 100:1 , чтобы получить ровную цифру. С реальным ОУ в этом нет нужды: при типовом усилении \(10\space^6\) коэффициент передачи с замкнутой петлёй составит \( G_{CL}\)=99.99 . <-
67 Как на схеме 2.53 в §2.3.5.C . <-
68 Если усиление без обратной связи A выражается действительным числом ( в значении «не комплЕксное», т.е. сдвига фаз нет ), тогда и выходной импеданс \(Z_{out}\) будет выражаться действительным числом ( т.е. будет резистивным \(R_{out}\) ) . Как будет понятно из Части _4 , A может выражаться комплЕксным числом и чаще всего именно им и выражается ), т.е. включает сдвиг фаз. Для ОУ этот сдвиг составляет 90° на большей части рабочей полосы. В результате выходной импеданс с замкнутой обратной связью имеет индуктивный характер. См., например, рис. 4.53 . <-
69 R. B. Blackman, “Effect of feedback on impedance”, Bell. Sys. Tech. J. 22, 269 ( 1943 ). <-
70 Это pun, дошло? ( That’s a pun, get it? ) - Нет, не дошло. <-
71 Те убогие, которым совсем БЮ невмочь, могут пропустить эту главу при первом знакомстве. [* Как это сделал я: ниасилил и свалил в «цифру» ] . <-

