2.3 (I) Модель Эберса-Молла в приложении к базовым транзисторным схемам
==90
На данный момент произошло знакомство с интересными схемами, которые можно разобрать, используя простейшую модель биполярного транзистора. Ключ, повторитель, источник тока и усилитель. И почти сразу обнаружились некоторые серьёзные ограничения. (Ну да, вы вообще готовы поверить в бесконечное усиление?! [* А оно есть ! Интегратор ( §4.2.6 ) - схема с «бесконечным усилением»] . ) Пора углубляться в детали, относящиеся к таким ограничениям. Дополнительных сведений будет достаточно для задач книги, и, что особенно приятно, для множества схем на биполярных транзисторах.
2.3.1 Уточнённая модель транзистора: источник тока, управляемый напряжением
Изменения касаются «правила _4 » ( §2.1.1 ). Ранее утверждалось, что \(I_C = β I_B\) . Транзистор рассматривался в качестве усилителя тока, чей вход с электрической точки зрения напоминал диод. В первом приближении картина верна и достаточна для некоторых задач. Но, чтобы разобраться с дифференциальными усилителями, логарифмическими преобразователями, температурной компенсацией и другими важными вещами, транзистор надо рассматривать как транскондуктивный элемент: ток коллектора определяется напряжением база-эмиттер.
==91
Вот новая редакция «правила 4»:
-
Транскондуктивный усилитель Если верны правила 1-3 ( §2.1.1 ), \(I_C\) зависит от \( V_{BE}\) в соответствии с уравнением 23
\[ I_C = I_S(T)\left(e^{\left[V_{BE}/V_T \right]} - 1\right ), \qquad \qquad [2.8] \] или иначе \[ V_{BE} = V_T\ln\left(\frac{I_C}{I_S(T)}+1\right ), \qquad \qquad [2.9] \] где \[ V_T = \frac{kT}{q} = 25.3 mV \quad \qquad \qquad \qquad [2.10] \] при комнатной температуре ( 20°C ), q - заряд электрона ( 1.6×10–19 кулон ), k - постоянная Больцмана ( 1.38×10–23 джоулей на кельвин, иногда обозначается \(k_B\) ) , T - абсолютная температура в градусах Кельвина ( K=°C+273.16 ) , а \(I_S( T ) \) - ток насыщения конкретного транзистора, который, как вскоре будет ясно, жёстко зависит от температуры ). Тогда ток базы, который тоже зависит от \( V_{BE}\) , можно аппроксимировать выражением \(I_B=I_C/β\) , где типичные значения «константы» β лежат в диапазоне 20...1000 , но зависят от типа транзистора, \(I_C\) , \( V_{CE}\) и температуры. \(I_S( T ) \) аппроксимируется обратным током утечки ( примерно 10–15A для малосигнальных транзисторов, вроде 2N3904 ). В активной области \(I_C ≫ I_S\) , т.е. член «–1» в [2.8] пренебрежимо мал по сравнению с выражением \[ I_C ≈ I_S(T)e^{\left[V_{BE}/V_T\right]}. \qquad \qquad \qquad [2.11] \]
Уравнение, описывающее \(I_C\) , называется «уравнением Эберса-Молла» 24 . Оно же ( при умножении на масштабный коэффициент из диапазона 1...2 ) подойдёт для примерного описания вольтамперной характеристики диода. В случае транзистора важно понимать, что ток коллектора определяется именно напряжением база-эмиттер, а не током базы ( последний примерно соответствует β ) . Данное экспоненциальное уравнение сохраняет точность в очень широком диапазоне токов: от наноампер до миллиампер. Рис. 2.41 показывает зависимость в графической форме 25 . Если измерять ток базы при различных токах коллектора, можно построить зависимость \(β\) от \(I_C\) , подобную изображённой на рис. 2.42 . Зависимость усиления транзистора от тока коллектора разбирается в Части X2 .
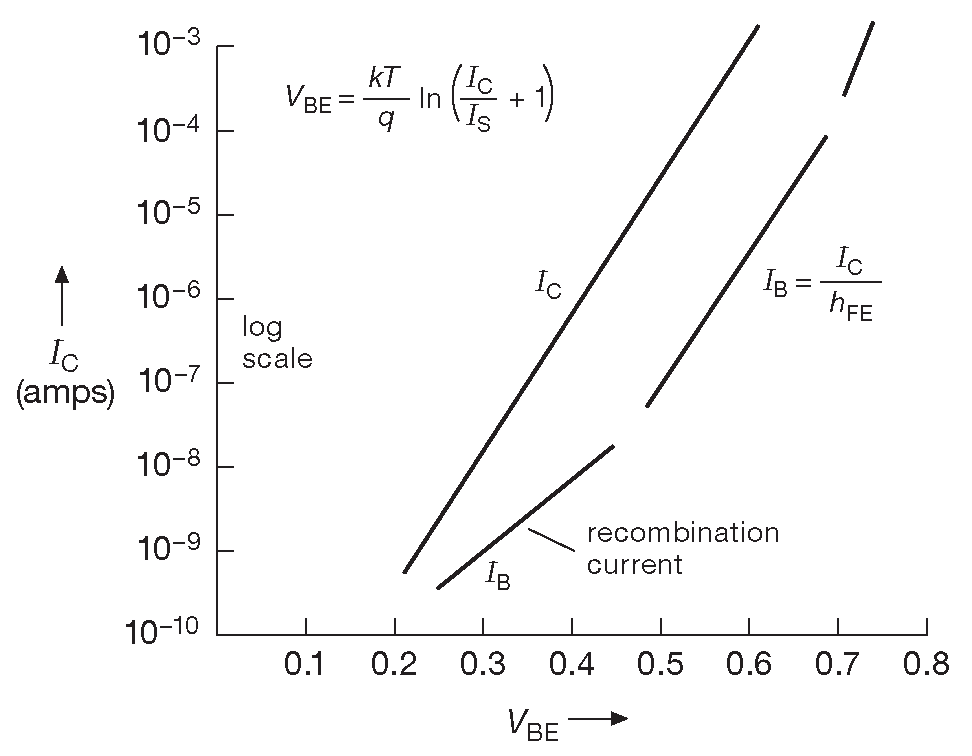
Рис. 2.41 Токи базы и коллектора как функции напряжения база-эмиттер \( V_{BE}\)
К сожалению, хотя уравнение Эберса-Молла сообщает зависимость тока коллектора от напряжения база-эмиттер, использовать его на практика, т.е. управлять транзистором, подавая на базу напряжение, затруднительно из-за слишком большой температурной зависимости \( V_{BE}\) . Позднее будет показано, как уравнение Эберса-Молла даёт правильное понимание проблемы и помогает её решить.
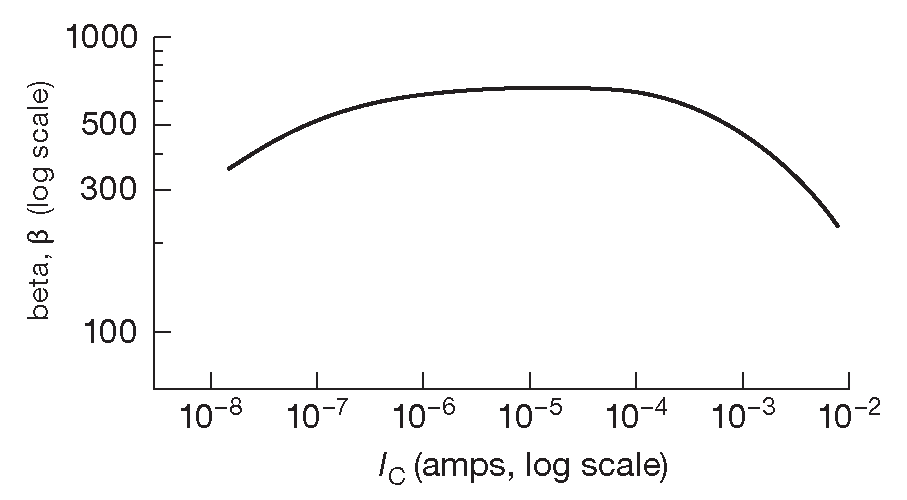
Рис. 2.42 Типичная зависимость усиления по току ( \(β\) ) от тока коллектора
2.3.2 Следствия модели Эберса-Молла: эмпирические правила для транзисторных схем
Из уравнения Эберса-Молла [2.8] можно получить простые и удобные «правила отношений» для тока коллектора: \[ \frac{I_{C2}}{I_{C1}}=\exp\left[\frac{Δ V_{BE}}{V_T}\right], \qquad \qquad ΔV_{BE}=V_T\ln\left(\frac{I_{C2}}{I_{C1}}\right ). \] Кроме того, при разработке будут активно использоваться некоторые важные параметры.
==92
2.3.2.A Крутизна ВАХ диода
На сколько нужно увеличить \( V_{BE}\) , чтобы \(I_C\) вырос в 10 раз? Из уравнения Эберса-Молла получается, что на \( V_T \ln10\)=58.2 mV при комнатной температуре. Удобно запомнить, что напряжение база-эмиттер увеличивается примерно на 60 mV на каждую декаду увеличения тока коллектора . Аналогично, \(I_C = I_{C0} · e^{[Δ V/25(mV)]}\) , где \(Δ V\) выражено в милливольтах 26 .
Ещё две формулировки.
- Ток коллектора удваивается на каждые 18 mV увеличения \( V_{BE}\).
- Ток коллектора увеличивается на 4% на каждый милливольт роста \( V_{BE}\).
2.3.2.B Импеданс со стороны эмиттера для малого сигнала при фиксированном напряжении на базе
Если взять производную из \( V_{BE}\) по \(I_C\) , то получится \[ r_e = \frac{V_T}{I_C} = \frac{25(mV)}{I_C} \qquad [Ω], \qquad [2.12] \] где \(I_C\) выражено в миллиамперах 27 . Числовое значение \( 25(mV)/I_C\) верно для комнатной температуры. Это внутреннее сопротивление эмиттера \( r_e\) , которое включается как бы последовательно с выводом эмиттера в любой транзисторной схеме. Именно оно ограничивает коэффициент передачи по току в усилителе с заземлённым эмиттером и уменьшает в повторителе коэффициент передачи по напряжению до величины чуть меньше единицы, не позволяя выходному импедансу опуститься до нуля. Отметим, что крутизна 28 усилителя с заземлённым эмиттером равна \[ g_m = \frac{I_C}{V_T} = \frac{1}{r_e} \qquad \qquad \qquad [2.13] \] ( или 40·\(I_C\) при комнатной температуре ).
2.3.2.C Температурная зависимость напряжения база-эмиттер
На первый взгляд из уравнения Эберса-Молла следует, что \( V_{BE}\) при постоянном токе коллектора имеет положительный коэффициент за счёт множителя T , входящего в \( V_T \) . Но большая температурная зависимость \(I_S(T) \) с избытком компенсирует воздействие предыдущего коэффициента, и в итоге \( V_{BE}\) ( при постоянном \(I_C\) ) уменьшается с коэффициентом 2.1 mV/°C и примерно пропорциональна 1/\( T_{abs}\) , где \( T_{abs}\) - абсолютная температура. Иногда удобнее использовать температурную зависимость \(I_C\) при постоянном \( V_{BE}\): ток \(I_C\) увеличивается со скоростью примерно 9%/°C и удваивается каждые 8°C роста температуры.
Есть ещё одна величина, которая иногда бывает нужна, хотя прямо из уравнения Эберса-Молла не следует. Она известна как «эффект Эрли» 29 и устанавливает важные ограничения на параметры источников тока и усилителей.
2.3.2.D Эффект Эрли
\( V_{BE}\) ( при постоянном \(I_C\) ) немного меняется при изменении \( V_{CE}\) . Эффект вызывается изменением ширины области базы при изменении \( V_{CE}\) и равен примерно \[ Δ V_{BE} = -η Δ V_{CE}, \qquad \qquad [2.14] \] где \(η = 10^{-5}...10^{-4}\) . Например, npn 2N5088 имеет \(η = 1.3 ×10^{-4}\) , т.е. \( V_{BE}\) изменяется на 1.3 mV при удержании тока коллектора на постоянном уровне и изменении \( V_{CE}\) на 10 V . Часто данное явление описывается как линейное изменение тока коллектора с увеличением напряжения на коллекторе при удержании \( V_{BE}\) на постоянном уровне. Зависимость выглядит следующим образом
==93
\[ I_C = I_{C0}\left(1 +\frac{V_{CE}}{V_A}\right ), \qquad \qquad [2.15] \] где \( V_A\) называется «напряжением Эрли» ( типичные значения 50...500 V ) 30 . В графической форме явление представлено на рис. 2.59 в §2.3.7.A . Низкая величина напряжения Эрли свидетельствует о низком выходном сопротивлении коллектора. Для pnp величина \( V_A\) в среднем ниже, чем для npn , см. табл. 8.1 . Эффект Эрли детально разбирается в Части X2 [* ##§X2.5 ] 31 .
Это весь список необходимых параметров. С их помощью можно решить большинство проблем транзисторных схем, поэтому чаще всего сама модель Эберса-Молла не потребуется 32 .
2.3.3 Повторный разбор эмиттерного повторителя
Перед повторным рассмотрением усилителя с общим эмиттером, учитывающим уточнённую модель транзистора, глянем свежим взглядом на эмиттерный повторитель. Модель Эберса-Молла сообщает, что эмиттер должен иметь ненулевой импеданс, даже если сигнал приходит с источника напряжения [* т.е. с низким \(R_S\)] , из-за вполне конкретной величины \( r_e\) ( см. 2.3.2.B ). По этой же причине усиление по напряжению чуть меньше единицы, т.к. \( r_e\) образует с сопротивлением нагрузки делитель.
Указанные факторы легко считаются. При постоянном напряжении на базе импеданс со стороны эмиттера равен \(R_{out} = dV_{BE}/dI_E\) , но \(I_E ≈ I_C\) , поэтому \(R_{out} ≈ r_e\) или внутреннему сопротивлению эмиттера ( напомним, \( r_e=25(mV)/I_C(mA )\) ) . Например, на рис. 2.43A нагрузка видит импеданс источника величиной \( r_e\)=25 Ω , потому что \(I_C\)=1 mA ( этот импеданс включён параллельно \(R_E\) [* для нагрузки, см. рис. 2.43B , на котором это лучше видно] , но на практике \(R_E\) всегда сильно больше \( r_e\) [* и, соответственно, мало влияет на итог] ). Рис. 2.43B показывает более жизненный вариант с ненулевой величиной \(R_S\) , но пока без цепи смещения и блокировочного конденсатора. Теперь выходной импеданс эмиттерного повторителя равен последовательно соединённым \( r_e\) и \(R_S/(β +1 ) \) ( и параллельным \(R_E\) , как и ранее ). Например, если \(R_S\)=1 kΩ , а \(I_C\)=1 mA , то \(R_{out}\)=35 Ω ( полагаем β=100 ). Легко показать, что внутреннее сопротивление эмиттера \( r_e\) влияет и на входной импеданс эмиттерного повторителя, как если бы он был включён последовательно с нагрузкой, вернее, с параллельным включением нагрузки и \(R_E\) . Другими словами, для эмиттерного повторителя эффект Эберса-Молла просто добавляет последовательное сопротивление эмиттера \( r_e\) к прежним цифрам 33 .
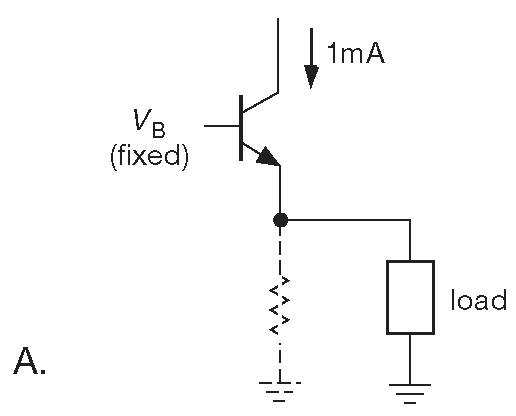
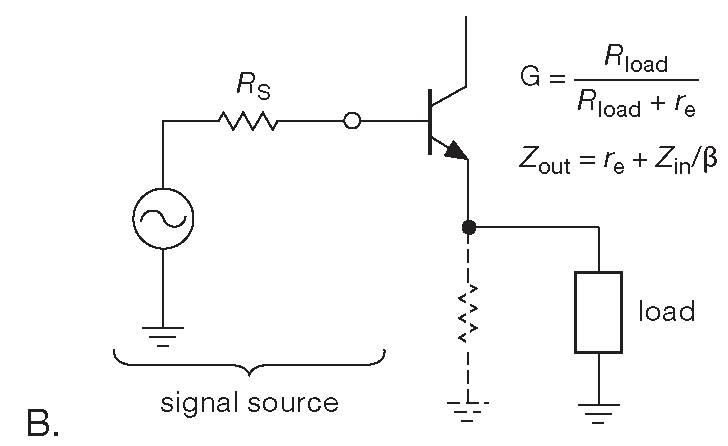
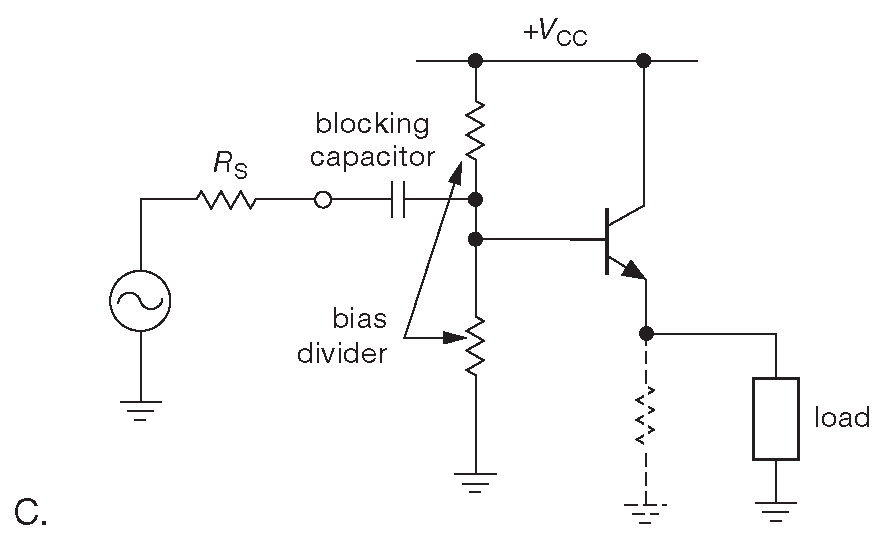
Рис. 2.43 Выходной импеданс эмиттерного повторителя ( см. сопровождающий текст )
Усиление по напряжению в эмиттерном повторителе немного ниже единицы из-за делителя, образованного \( r_e\) и сопротивлением нагрузки. Его, опять же, легко подсчитать, потому что выход находится в точки соединения \( r_e\) и \(R_{load}\) . \[ G_V=\frac{v_{out}}{v_{in}} = \frac{R_L}{( r_e+R_L )}. \] Таким образом, повторитель с током покоя 1 mA и нагрузкой 1 kΩ имеет усиление по напряжению 0.976 . Усиление часто выражают через крутизну, чтобы охватить заодно и полевые транзисторы ( §3.2.3.A ). В этом случае, считая, что \( g_m\)=1/\( r_e\) , получаем \[ G_V = \frac{R_L · g_m}{(1+R_L · g_m)}. \]
2.3.4 Повторное рассмотрение усилителя с общим эмиттером
Старая модель давала неверную величину коэффициента передачи по напряжению усилителя с общим эмиттером с эмиттерным резистором ( его называют схемой с эмиттерной дегенерацией ). Ошибка возникает, если такой эмиттерный резистор равен нулю: \[ G_V=-\frac{R_C}{R_E}= ∞. \]
На самом деле транзистор имеет внутреннее сопротивление эмиттера \( r_e=25(mV)/I_C(mA ) \) , которое нужно добавлять к внешнему эмиттерному резистору. Цифра становится заметна, только когда внешний резистор мал или отсутствует вовсе 34 . Поэтому, например, рассмотренный ранее усилитель с заземлённым эмиттером имеет коэффициент передачи –10 kΩ/\(r_e\)=–400 . Входной импеданс также не нулевой, как следовало из старой модели ( \(β R_E\) ) и равен примерно \(β r_e\) . В данном случае ( ток покоя 1 mA ) он равен примерно 2.5 kΩ 35 .
==94
Термины «заземлённый эмиттер» и «общий эмиттер» часто путают, что может смутить неподготовленного человека. В книге используется фраза «усилитель с заземлённым эмиттером», которая означает усилитель с общим эмиттером с \(R_E\)=0 ( или с шунтирующим конденсатором ). Усилитель с общим эмиттером имеет резистор в эмиттере [* просто иногда он равен нулю] . Важно лишь то, что цепь эмиттера является общей для входной и для выходной цепи [* к примеру, у эмиттерного повторителя эмиттер подключён к нагрузке, и его цепь не является общей с источником сигнала ] .
2.3.4.A Недостатки однокаскадного усилителя с заземлённым эмиттером
Дополнительное усиление по напряжению, которое появляется при \(R_E\)=0 идёт в комплекте с кое-какими другими особенностями. Фактически данной схемы включения, несмотря на её частое упоминание в учебной литературе, следует избегать везде, кроме устройств с общей обратной связью. Чтобы понять, почему это так, рассмотрим рис. 2.44 .
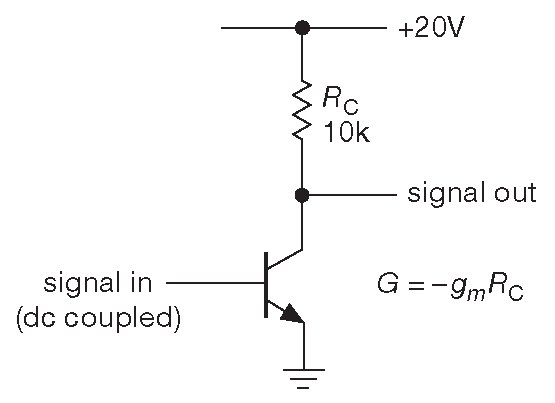
Рис. 2.44 Усилитель с общим эмиттером без эмиттерной дегенерации
- 1. Нелинейность
- Усиление по напряжению \[ G=-R_Cg_m=-R_C\frac{1}{r_e}=-R_C\frac{I_C(mA )}{25(mV)}, \] поэтому для тока покоя 1 mA усиление равно –400 . Но \(I_C\) меняется вместе с изменением сигнала. В примере получаем изменение \( G\) от –800 ( \( V_{out}\)=0 , \(I_C\)=2 mA ) до 0 ( \( V_{out} = V_{CC}, I_C\)=0 ). Для треугольного сигнала выход будет выглядеть как на рис. 2.45 . Усилитель очень нелинеен, т.е. имеет большие искажения. Такая схема без обратной связи подходит только для малых колебаний вокруг точки покоя. И наоборот, усилитель с эмиттерной дегенерацией имеет коэффициент передачи, практически полностью независимый от тока коллектора до тех пор, пока \(R_E ≫ r_e\) . Такой усилитель не будет иметь искажений даже для сигнала большой амплитуды.
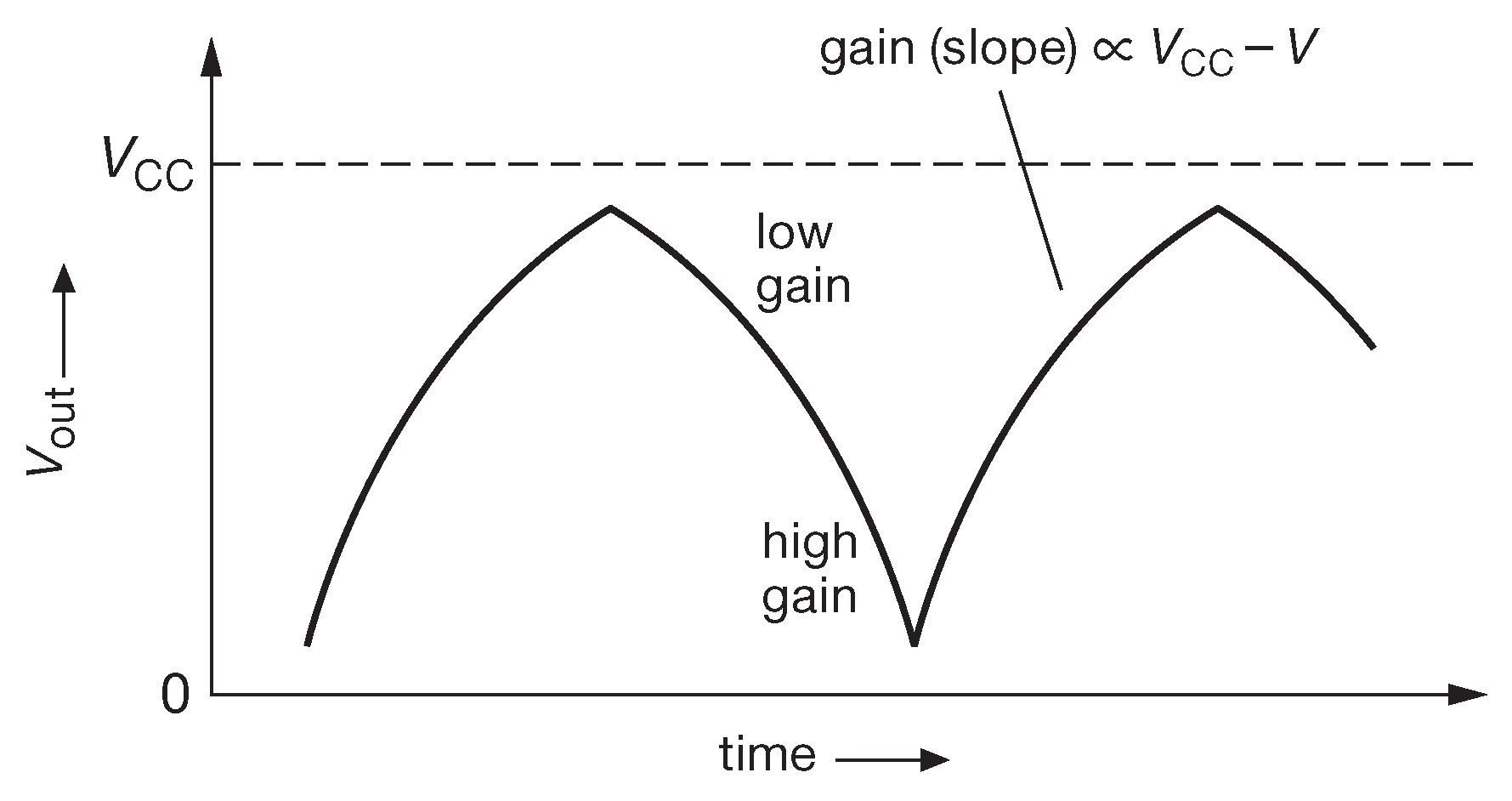
Рис. 2.45 Нелинейный выходной сигнал усилителя с заземлённым эмиттером
Оценим искажения с эмиттерным резистором и без него. С заземлённым эмиттером усиление для малого сигнала равно \[ G_V=-\frac{R_C}{r_e}=-\frac{I_CR_C}{V_T}=-\frac{V_{drop}}{V_T}, \] где \( V_{drop}\) - текущее падение напряжения на коллекторном резисторе. Усиление пропорционально \( V_{drop}\) , поэтому нелинейность ( та доля усиления, которая меняется с изменением сигнала ) равна отношению мгновенного [* отклонения] падения на коллекторном резисторе [* от среднего] к среднему ( при токе покоя ): \[ \frac{Δ G}{G} ≈ \frac{Δ V_{out}}{V_{drop}}, \] где \( V_{drop}\) - среднее ( при токе покоя ) падение на коллекторном резисторе \(R_C\) . Т.к. формула отражает экстремальное изменение усиления ( на пиках сигнала ), величина «искажений», обычно определяемая как амплитуда сигнала после вычитания линейной компоненты, будет примерно в 3 раза меньше. Отметим, что искажения зависят только от отношения сигнала к падению при токе покоя, а не от величины самого тока.
==95
Как пример, для усилителя с заземлённым эмиттером, запитанного от +10 V , с рабочей точкой на половине питания ( т.е. \( V_{drop}\space\)=5V ) измерения показывают искажения 0.7% для синусоидального сигнала амплитудой 0.1V и 6.6% для 1V . Цифры хорошо согласуются с расчётами. Можно сравнить этот результат с данными для \(R_E\) . Усиление \[ G_V=-\frac{R_C}{( r_e+R_E )}=-\frac{I_CR_C}{( V_T+I_CR_E )}. \] Искажения увеличивает только первое слагаемое делителя, поэтому они уменьшаются в той же степени, в которой \( r_e\) меньше общего действующего сопротивления в эмиттере. Нелинейность равна \[ \frac{Δ G}{G} ≈ \frac{Δ V_{out}}{V_{drop}} · \frac{r_e}{( r_e+R_E )} = \frac{Δ V_{out}}{V_{drop}} · \frac{V_T}{( V_T+I_ER_E )}. \] Второй сомножитель - коэффициент уменьшения искажений. Если подобрать эмиттерный резистор, чтобы падение на нём в состоянии покоя равнялось 0.25 V , то уменьшение искажений по этим расчётам составит 10× . Результаты измерений дают 0.08% для 0.1V и 0.74% для 1V , соответственно. И опять результат измерений хорошо согласуется с теорией.
Упражнение 2.12
Посчитайте теоретические уровни искажений для обеих схем для измеренных уровней выходного сигнала.
Как уже отмечалось, нелинейность усилителя с общим эмиттером превращает входной треугольный сигнал в «крышу на сарае», показанную на рис. 2.45 36 . Для сравнения на рис. 2.46 приводится реальная осциллограмма работы такого усилителя. Использовался 2N3904 с резистором 5 kΩ в коллекторе с питанием +10 V и рабочей точкой ( которую приходится выставлять очень аккуратно ) на половине питания. С помощью линейки [* по касательной к графику] было установлено мгновенное значение усиления на уровне +5V ( половина от \( V_+\) , ток коллектора 1 mA ) и +7.5 V ( ток коллектора 0.5 mA ). Значения хорошо согласуются с расчётами \[ G=\frac{R_C}{r_e}=\frac{I_C(mA )R_C}{25(mV)} \] усиление составляет –200 для +5V и –100 для +7.5 V . Для сравнения на рис. 2.47 показано, как меняется картинка при добавлении в эмиттер резистора 225 Ω . Для точки покоя усиление уменьшается в 10 раз [* откуда, собственно, и термин «эмиттерная дегенерация» - «ухудшение», «вырождение»] \[ G=\frac{R_C}{( R_E+r_e )} ≈ \frac{R_C}{250 Ω}, \] а линейность растёт, потому что изменение \( r_e\) составляет лишь малую часть общего сопротивления в знаменателе. Теперь основная доля в сопротивлении приходится на резистор 225 Ω .
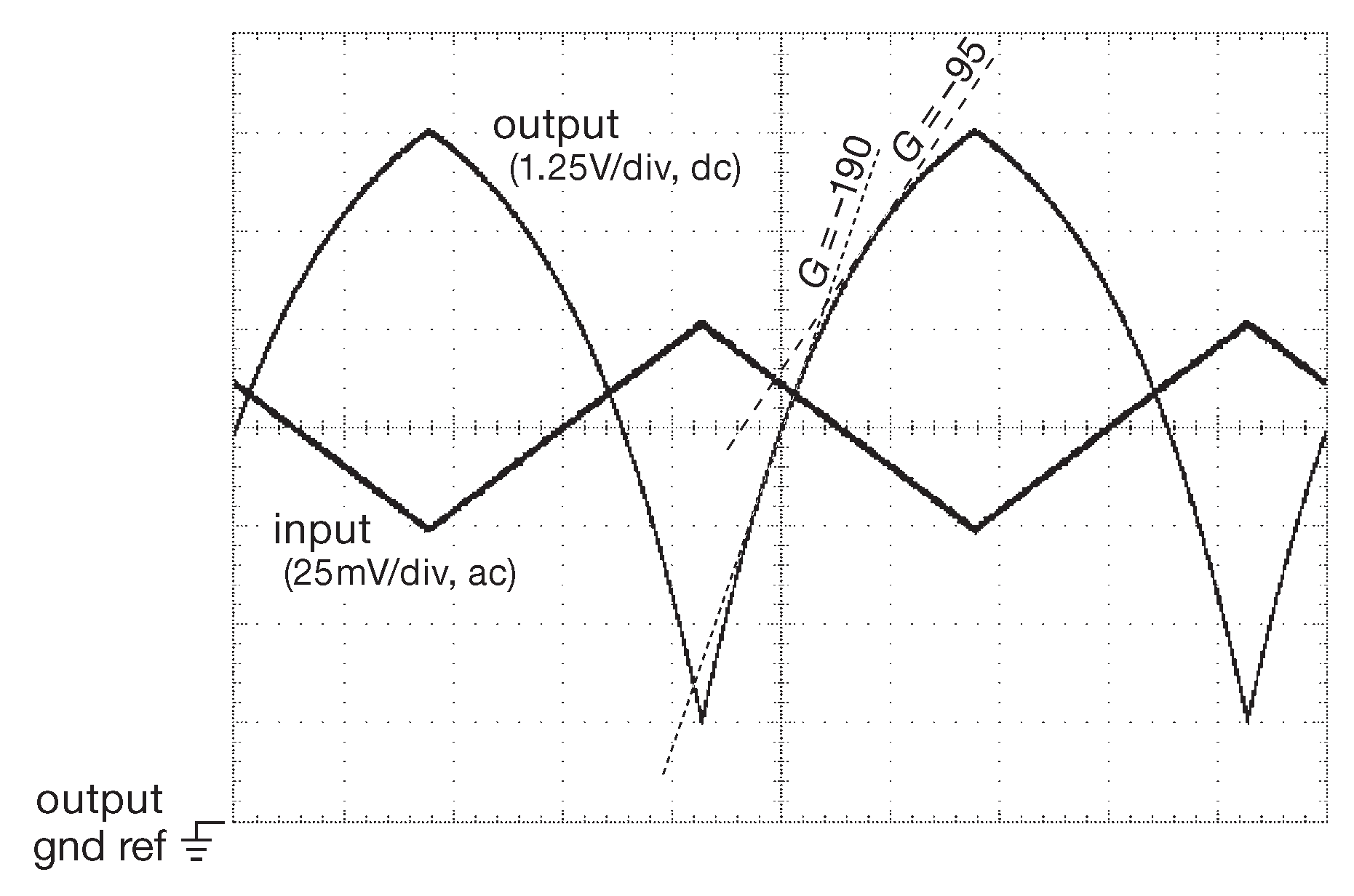
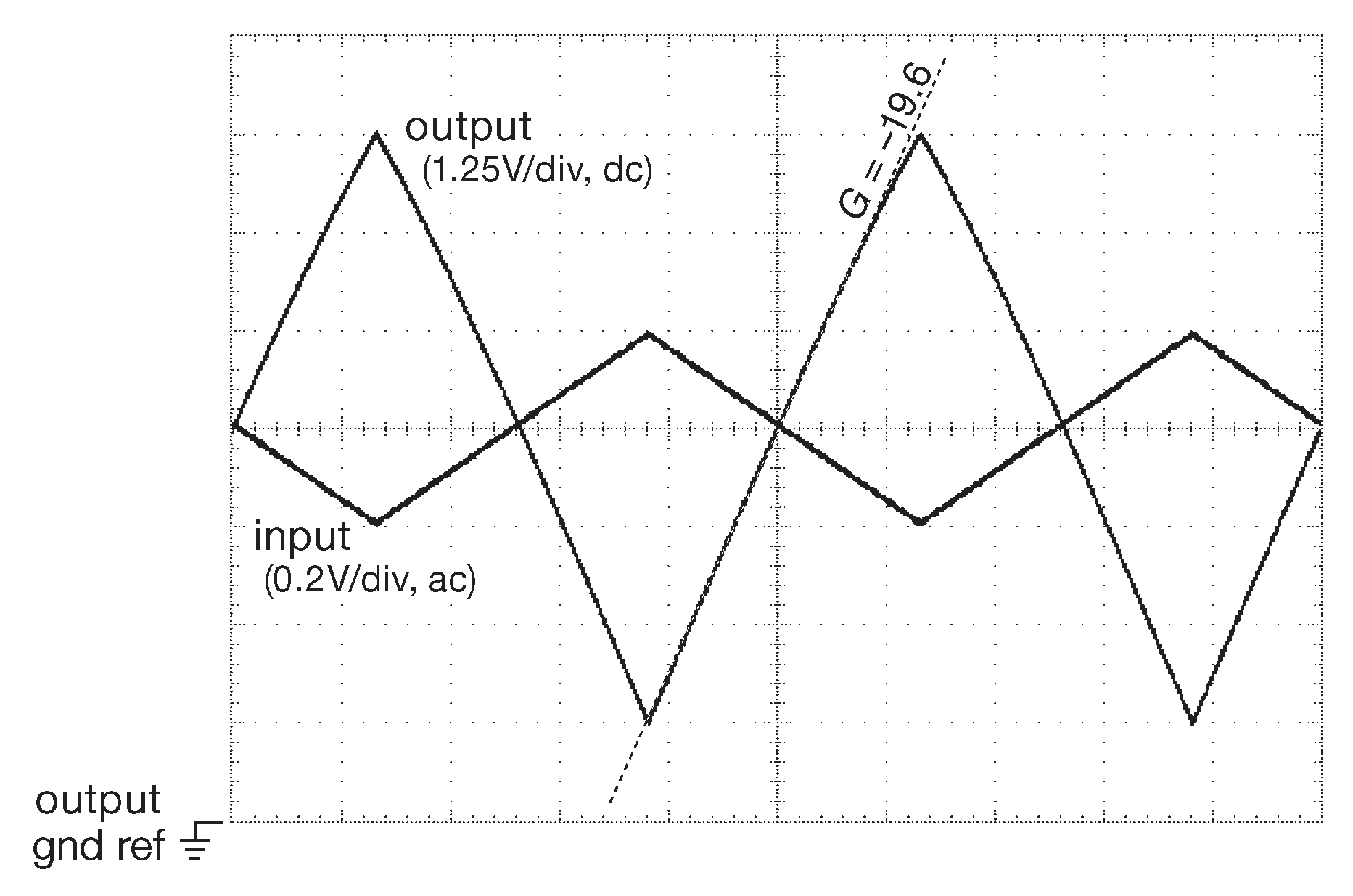
Рис. 2.46 Жизненные реалии . Усилитель с заземлённым эмиттером ( рис. 2.44 ) с \(R_C\)=5 kΩ , \( V_+\)=+10 V и треугольным входным сигналом частотой 1 kHz . Верхняя и нижняя границы экрана соответствуют +10 и 0V для выходного сигнала со связью по постоянному току. Обратите внимание на разные цифры вертикального разрешения для входного и выходного сигнала. Оценочная величина усиления ( касательные ) даны для \( V_{out}\)=0.5\( V_+\) и \( V_{out}\)=0.75\( V_+\) . По горизонтали 0.2 ms/div
Рис. 2.47 Эмиттерный резистор величиной 225 Ω кардинально улучшает линейность ценой снижения усиления ( оно падает в 10 раз при заданном токе покоя ). По горизонтали 0.2 ms/div
Для синусоидального сигнала на входе выход содержит все гармоники основной частоты [* появляющиеся из-за искажений, т.к. в идеальной линейной системе была бы одна основная частота ] . Позднее будет рассказано, как сделать из двух транзисторов дифференциальный усилитель, имеющий симметричное распределение искажений, спектр которого содержит только нечётные гармоники. В Части X2 рассказывается о нескольких интересных методах компенсации искажений в дифференциальных усилителях и использовании моделирования в SPICE для быстрой оценки и коррекции параметров схемы ( §X2.4 ). Наконец, стоит добавить, что остаточные искажения в усилителях могут быть существенно снижены за счёт отрицательной обратной связи . Обратная связь разбирается в §2.5 после знакомства с популярными транзисторными схемами. Обратная связь занимает центральное место в теме операционных усилителей в Части _4 .
- 2. Входной импеданс
- Входной импеданс грубо оценивается, как \(Z_{in}(Ω)= β×r_e = β×25(mV)/I_C(mA ) \) . Вновь изменение тока коллектора вместе с изменением сигнала приводит к вариациям входного импеданса. Если исключить ситуацию с низкоомным источником в базе, то нелинейный делитель из импедансов источника и усилителя дополнительно увеличивает искажения. А при наличии эмиттерного сопротивления входное усиление велико и почти постоянно.
==96
- 3. Смещение
- В усилителе с заземлённым эмиттером трудно задавать рабочую точку. Может показаться, что достаточно подать потенциал в базу с делителя напряжения, чтобы получить нужное соотношение в соответствии с уравнением Эберса-Молла. Этот метод не работает, потому что имеется температурная зависимость \( V_{BE}\) ( при постоянном \(I_C\) ) величиной 2.1 mV/°C . \( V_{BE}\) снижается с увеличением температуры T , потому что \(I_S(T) \) также меняется, и в результате \( V_{BE}\) примерно пропорционально 1/T , где T - абсолютная температура. Это значит, что ток коллектора для фиксированного \( V_{BE}\) будет увеличиваться в 10 раз на каждые 30°C роста температуры ( такая разница соответствует 60 mV изменения \( V_{BE}\) ) или примерно на 9%/°C . Столь нестабильная рабочая точка совершенно бесполезна, потому что при малейших колебаниях температуры усилитель будет входить в насыщение. Например, усилитель с заземлённым эмиттером, смещённый так, чтобы коллектор был на половине питания, войдёт в насыщение, если температура изменится на 8°C .
Упражнение 2.13
Покажите, что при росте температуры на 8°C усилитель с заземлённым эмиттером, смещённый делителем напряжения, войдёт в насыщение. Предполагается, что исходное смещение составляет \( V_C\)=0.5\( V_{CC}\) .
Некоторые возможные решения разбираются ниже. А вот усилитель с эмиттерной дегенерацией стабилен при подаче постоянного потенциала в базу, т.к. большая часть этого напряжения появится на эмиттерном резисторе, который и будет задавать ток покоя.
2.3.4.B Эмиттерный резистор в качестве обратной связи
Параметры усилителя с общим эмиттером можно улучшить, если последовательно с внутренним сопротивлением эмиттера \( r_e\) добавить внешний резистор ( эмиттерную дегенерацию ). Ценой улучшения будет снижение усиления. Та же картина будет наблюдаться в Части _4 и _5 [* и в §2.5 ] , где будет рассматриваться отрицательная обратная связь . Это важный приём, позволяющий улучшить параметры, расходуя часть выходного сигнала на компенсацию части сигнала на входе. Сходство здесь не случайно: усилитель с эмиттерной дегенерацией использует одну из форм отрицательной обратной связи [* см. §X2.4.4 ] . Транзистор можно рассматривать как транскондуктивный прибор, ток коллектора ( т.е. и выходное напряжение ) которого зависят от напряжения между базой и эмиттером. Но на входе сигнал между базой и землёй . Значит, напряжение база-эмиттер равно входному напряжению минус часть выходного ( здесь \(I_ER_E\) ) . Это и есть отрицательная обратная связь, которая улучшает многие параметры усилителя ( линейность и стабильность, плюс повышает входной импеданс 37 ). В §2.5 произойдёт первое знакомство с обратной связью, и эффект будет оценен численно. Основное рассмотрение отложено до Части _4 и _5 .
2.3.5 Смещение в усилителе с общим эмиттером
Если требуется максимальное усиление ( или каскад охвачен отрицательной обратной связью ), то приходится организовывать правильную цепь смещения для схемы с общим эмиттером. Есть три способа, которые можно применять вместе или по отдельности: шунтирование эмиттерного резистора, согласованный транзистор в цепи смещения и обратная связь по постоянному току.
2.3.5.A Шунтирование эмиттерного резистора
Эмиттерный резистор в усилителе с дегенерацией можно шунтировать по схеме 2.48 . В этом случае выбирается \(R_E\)≈0.1\(RC\) для удобства смещения. Если \(R_E\) слишком мал, то напряжение на эмиттере будет мало, по сравнению с падением база-эмиттер. Это вызовет температурный дрейф рабочей точки из-за ТКН \( V_{BE}\) . Шунтирующий конденсатор должен иметь на нижней границе частоты сигнала небольшой импеданс, по сравнению с \( r_e\) ( не \(R_E\) , почему? ). Для схемы 2.48 он равен 25 Ω на 650 Hz . На частоте сигнала входной блокирующий конденсатор будет видеть импеданс 10 kΩ [* делитель в базе ] параллельно с входным импедансом базы \(β\)×25 Ω≈2.5 kΩ . На постоянном токе импеданс будет гораздо выше: \(β ×R_E\)≈100 kΩ .
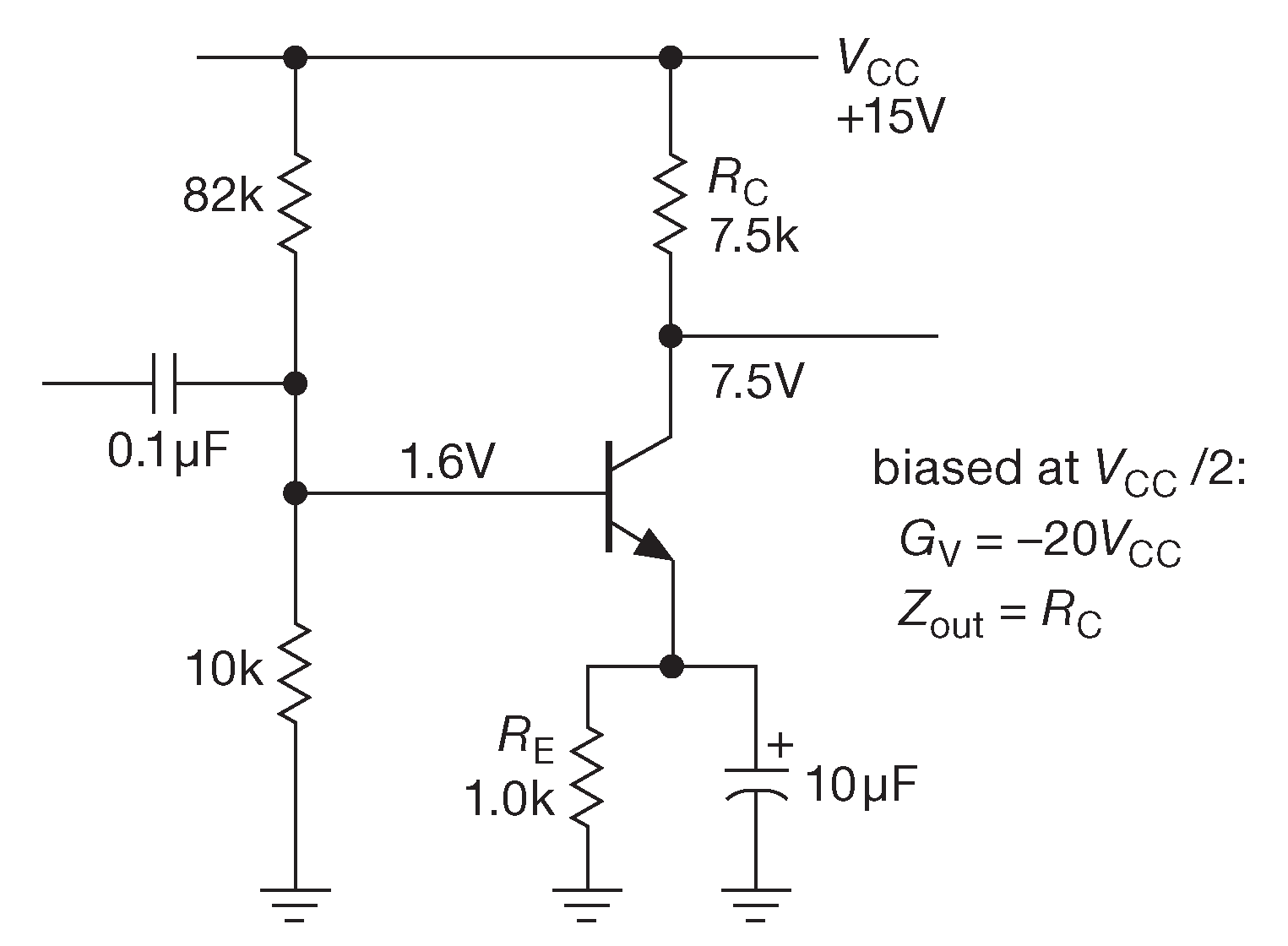
Рис. 2.48 Шунтированный резистор в эмиттере можно использовать, чтобы улучшить стабильность рабочей точки в усилителе с заземлённым эмиттером
==97
Вариант схемы состоит из двух последовательных эмиттерных резисторов, один из которых шунтирован. Например, предположим, что нужен усилитель с \( G_V\)=50 , током покоя 1 mA , питанием +20 V и рабочей полосой 20 Hz...20 kHz . Если задействовать схему эмиттерной дегенерации, то получится вариант с рис. 2.49 . Коллекторный резистор выбирается, чтобы напряжение покоя составляло 0.5\( V_{CC}\) . Следом под требуемое усиление подбирается эмиттерный резистор, который должен учитывать эффект \( r_e\)=25\((mV)/I_C(mA ) \) . Проблема в том, что напряжение на эмиттере всего 0.175 V . Оно будет существенно меняться, когда падение база-эмиттер величиной 0.6 V будет ползти от температуры ( ТКН ≈–2.1 mV/°C ), т.к. делитель \(R_1R_2\) удерживает на базе постоянный потенциал. Можно проверить, что при изменении температуры на 20°C ток коллектора увеличится на 25% .
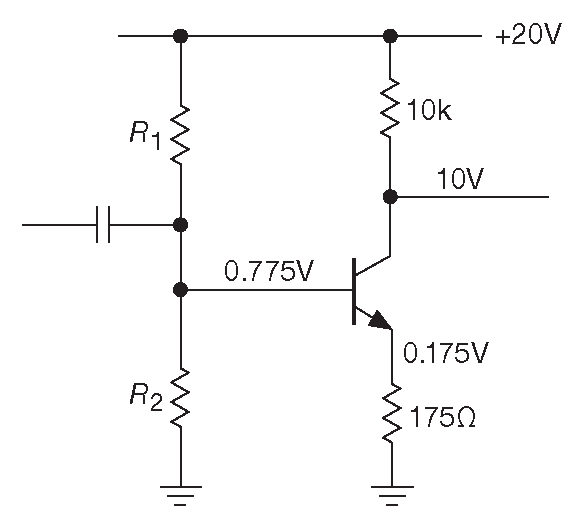
Рис. 2.49 Каскад усиления ×50 , имеющий проблемы со стабильностью рабочей точки
Упражнение 2.14
Подтвердите данное утверждение
В этой схеме поможет шунтирование сопротивления в эмиттере, которое стабилизирует рабочую точку, но не портит усиление на частоте сигнала ( рис. 2.50 ).
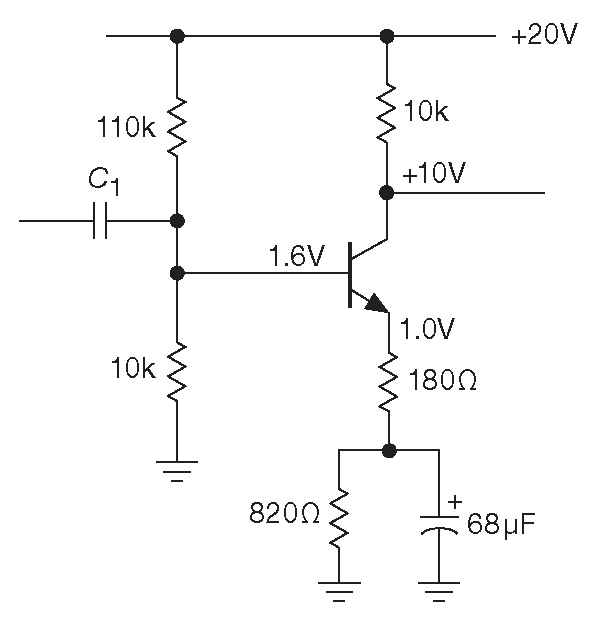
Рис. 2.50 Каскад усиления с общим эмиттером, в котором сочетаются стабильность рабочей точки, линейность и большое усиление
- Как и ранее, резистор в коллекторе выбирается под нужное напряжение на коллекторе ( 10 V=0.5\( VCC\) ).
- Затем под нужное усиление ( ×50 ) подбирается резистор в эмиттере без учёта шунтирования, но с учётом внутреннего \( r_e=25(mV)/I_C(mA ) \) [* пока получаем всё те же номиналы, что и ранее ] .
- Теперь добавляем резистор с шунтированием для стабилизации рабочей точки [* чтобы изменение \( V_{BE}\) от температуры составляло незначительную часть от общего падения база-земля] . Здесь хорошим ориентиром служит 1/10 от величины сопротивления в коллекторе [* для суммарного сопротивления в эмиттере ] .
- Теперь выбирается потенциал базы, который обеспечит эмиттерный ток 1 mA [* ток покоя] , с импедансом в 10 раз меньшим, чем получившийся импеданс транзистора со стороны базы ( здесь около 100 kΩ ).
- Шунтирующий конденсатор должен иметь низкий импеданс по сравнению с 180+\( r_e\)=200 Ω на нижней границе рабочего диапазона. Наконец, входной разделяющий конденсатор должен иметь низкий импеданс по сравнению со входным импедансом усилителя на рабочей частоте . Он равен импедансу входного делителя в параллель с \(β\)×(180+25)Ω ( т.к. 820 Ω шунтированы и выглядят как короткое замыкание на частое сигнала ).
Альтернативная схема разделяет путь сигнала по постоянному и переменному току ( рис. 2.51 ). Это позволяет менять усиление, изменяя резистор 180 Ω , не меняя смещения.
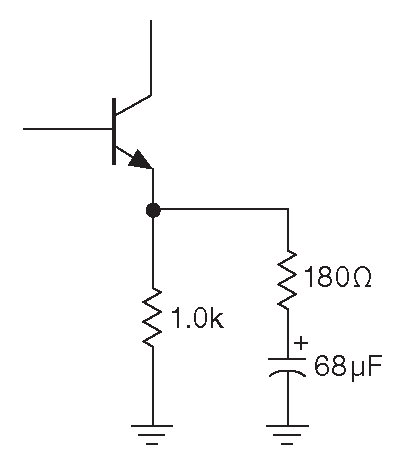
Рис. 2.51 Эквивалентная схема эмиттерной цепи с рис. 2.50
2.3.5.B Согласованный смещающий транзистор
Для получения правильного напряжения смещения под нужный ток коллектора можно использовать согласованный с основным транзистор. Такой способ предполагает автоматическую температурную компенсацию ( рис. 2.52 ) 38 . Коллектор \(Q_1\) забирает ток 1 mA , т.к. он гарантированно имеет близкий к земле потенциал ( на \( V_{BE}\) выше, если точнее ). Если \(Q_1\) и \(Q_2\) - согласованная пара, т.е. транзисторы, сделанные зацело из одного куска кремния, тогда \(Q_2\) также будет забирать 1 mA , устанавливая потенциал коллектора точно на +10 V и допуская полный симметричный размах сигнала на выходе ±10 V . Изменение температуры на ситуацию не влияет до тех пор, пока она одинаковая для обоих транзисторов. Это серьёзный аргумент в пользу «монолитных» сдвоенных транзисторов.
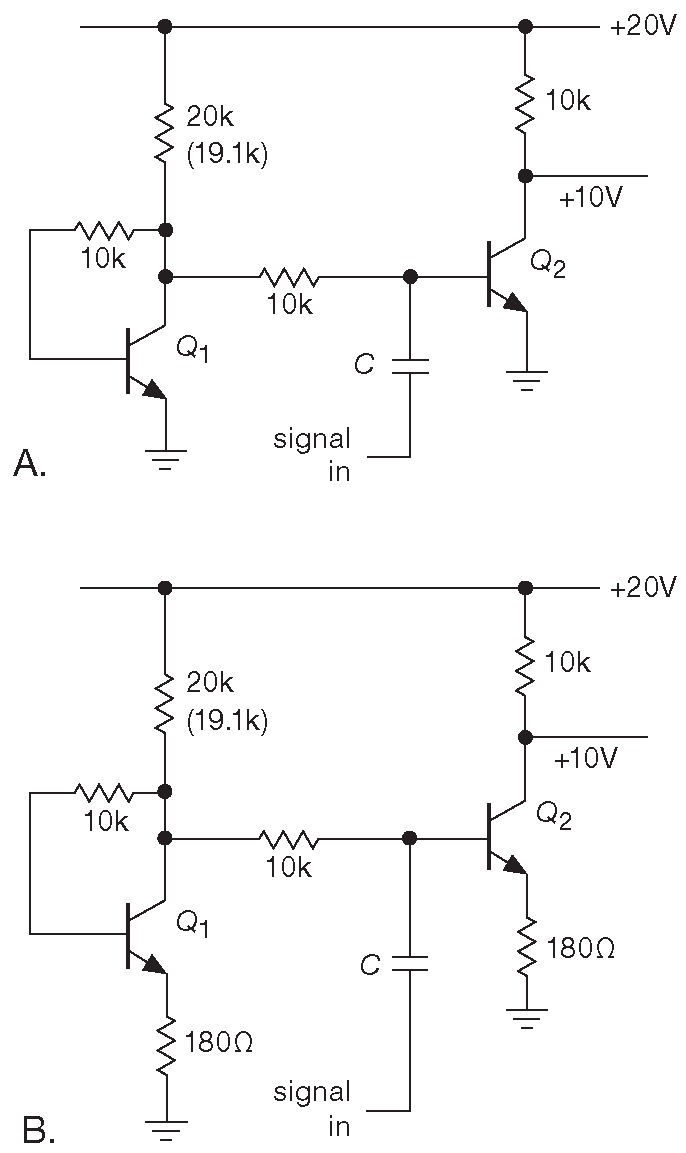
Рис. 2.52 Схема смещения, учитывающая изменение \( V_{BE}\) с температурой как для заземлённого эмиттера (A) , так и для варианта с эмиттерной дегенерацией (B) . С указанными номиналами \( V_C\) будет примерно +10.5 V , а, если сократить 20 kΩ до 19.1 kΩ ( ближайшее стандартное значение ), то будут учтены вариации \( V_{BE}\) и величина \(β\) , и на коллекторе будет +10 V
==98
2.3.5.C Обратная связь по постоянному току
Для стабилизации рабочей точки можно использовать обратную связь по постоянному току. Один метод показан на рис. 2.53A . Снимая напряжение для смещающего делителя с коллектора, а не с положительного питания, можно до некоторой степени улучшить стабильность тока покоя. Рабочая точка установлена на один p-n переход выше земли, но так как её уровень равен напряжению на средней точке делителя 10:1 , верхняя точка делителя - коллектор - должен быть на 11 p-n переходов выше земли, т.е. в районе 7V . Попытка транзистора войти в насыщение ( например, очень большая бета или изменение температуры ) снижает потенциал коллектора и через делитель понижает напряжение на базе, т.е. блокирует насыщение. Таким образом, рабочая точка стабилизируется. Это вполне рабочая схема, если высокая стабильность не нужна, но сама рабочая точка гуляет примерно на вольт при изменении температуры кристалла, потому что падение база-эмиттер имеет высокий температурный коэффициент ( см. уравнение Эберса-Молла [2.11] ). Большей стабильности можно добиться, добавив усиления в обратную связь. В теме обратной связи будет показано несколько примеров.
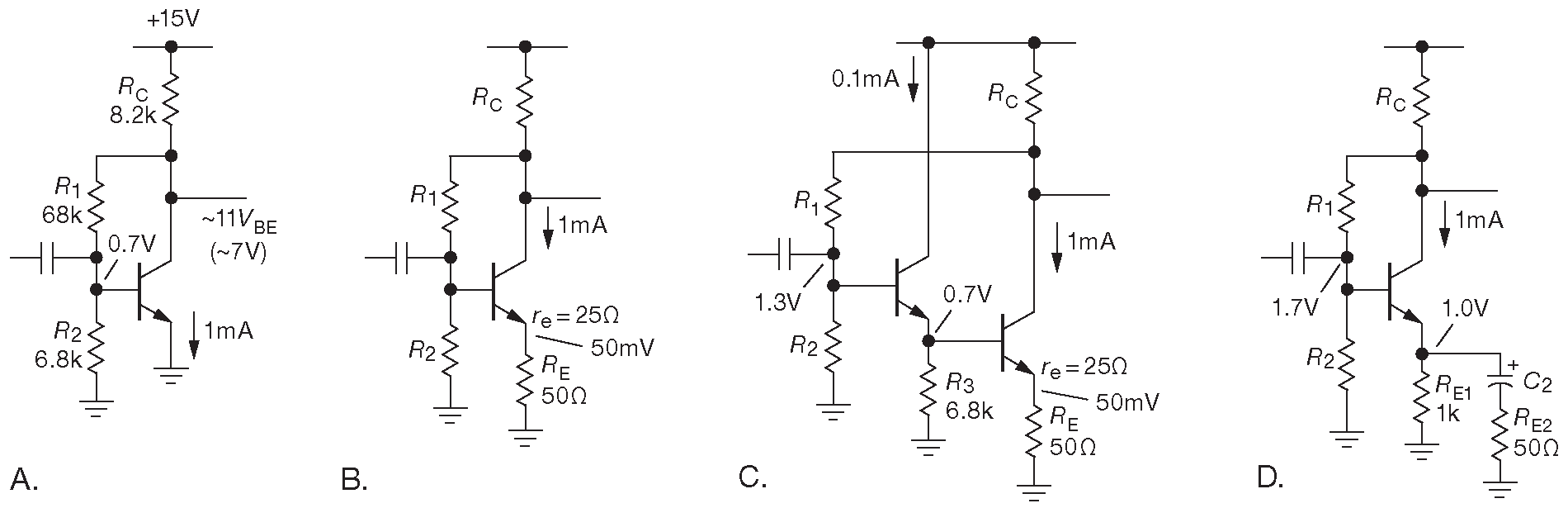
Рис. 2.53 Увеличение стабильности смещения за счёт обратной связи
Для понимания принципов работы этой схемы требуется знание обратной связи. Скажем, обратная связь уменьшает входной и выходной импеданс [* т.е. имеем параллельную ( уменьшает входной импеданс) обратную связь по напряжению ( уменьшает выходной )] . Сигнал видит на входе \(R_1\) , номинал которого снижен с коэффициентом передачи каскада. В данном случае до 200 Ω на землю, что совершенно неприемлемо. Чуть дальше ( и в Части _4 ) обратная связь будет разбираться детально, что позволит рассчитать усиление по напряжению схемы и её входной и выходной импеданс.
На рис. 2.53B-D показаны некоторые вариации базовой схемы обратной связи по постоянному току. На рис. 2.53B добавлена эмиттерная дегенерация, чтобы улучшить линейность и предсказуемость усиления. В схеме 2.53C появляется входной повторитель, увеличивающий входной импеданс ( номиналы резисторов входного делителя требуется соответственно увеличить и изменить их отношение, чтобы учесть второе падение \( V_{BE}\) ) . Схема 2.53D объединяет 2.53B и 2.51 , чтобы увеличить стабильность смещения.
Отметим, что номиналы резисторов смещения в схеме можно увеличить, чтобы поднять входной импеданс, но следует учитывать отнюдь не нулевой входной ток базы. Здесь подойдут \(R_1\)=220 kΩ и \(R_2\)=33 kΩ . Ещё один вариант - развязать резистор обратной связи ( рис. 2.54 ), чтобы подавить обратную связь ( а значит, поднять входной импеданс) на частотах сигнала 39 .
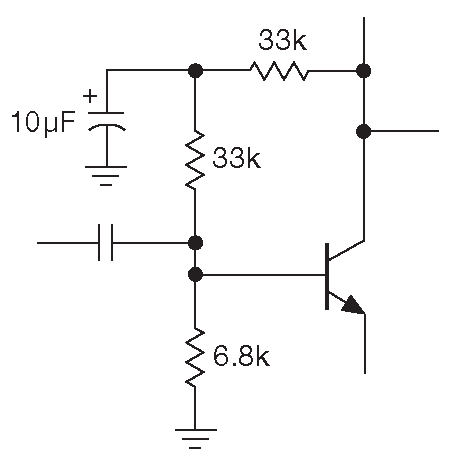
Рис. 2.54 Подавление обратной связи, снижающей входной импеданс на частотах сигнала
[* На частоте сигнала средняя точка 33 kΩ+33 kΩ имеет за счёт конденсатора 10 μF низкий импеданс, и сигнал с коллектора перестаёт проходить в базу, «утекая» в низкоимпедансный узел, а на постоянном токе цепь выглядит как схема 2.53A ] .
2.3.5.D Замечание о смещении и усилении
Важное замечание об усилителях с заземлённым эмиттером. Возможно, вы думаете, что коэффициент передачи по напряжению можно поднять, увеличив ток покоя, т.к. при этом внутреннее сопротивление эмиттера \( r_e\) снижается. Оно и в самом деле снижается, но увеличившийся ток потребует меньшего номинал коллекторного резистора, чтобы сохранить прежнее напряжение смещения на выходе. Это убьёт все плюсы. Можно показать, что усиление по малому сигналу в каскаде с заземлённым эмиттером, смещённым на 0.5\( V_{CC}\) , не зависит от тока покоя и равно 20\( V_{CC}\) , где \( V_{CC}\) выражено в вольтах.
Упражнение 2.15
Подтвердите данное утверждение.
==99
Если требуется получить на одном каскаде большее усиление, поможет активная нагрузка в виде источника тока. Такой вариант позволяет поднять коэффициент передачи до 1000 и более за счёт очень высокого импеданса активной нагрузки 40 . Но на описанных здесь схемах такой приём использовать нельзя, т.к. он подразумевает наличие общей обратной связи по постоянному току, которая будет разбираться позднее в Части _4 . [* Дело в том, что усилитель с коэффициентом передачи 1000 и питанием ±10 V достигнет уровня ограничения уже при сигнале 10 V/1000=10 mV , т.е. войдёт в насыщение от косого взгляда, и без обратной связи будет совершенно бесполезен] . Кроме того, подобный каскад должен работать на высокоомную нагрузку, в противном случае всё усиление, приобретённое за счёт активной нагрузки в коллекторе, будет потеряно. Подойдёт эмиттерный повторитель, полевой транзистор или операционный усилитель.
В радиочастотных усилителях, работающих в узких диапазонах частот, общепринятой практикой является использование параллельных LC контуров в качестве коллекторной нагрузки. Такая схема позволяет получить очень высокое усиление по напряжению, т.к. LC цепи имеют высокий импеданс ( подобно источнику тока ) на частотах сигнала и низкий на постоянном токе. Из-за того, что контур «настроен» на определённую частоту, все посторонние внеполосные сигналы ( и гармоники ) отлично подавляются. Дополнительным бонусом идёт возможность получить двойной размах на выходе, а индуктивность позволяет организовать трансформаторную связь.
Упражнение 2.16
Разработайте усилитель с общим эмиттером, настроенный на частоту 100 kHz . Используйте эмиттерный резистор с шунтированием. Рабочий ток 1 mA , питание \( V_{CC}\)=15 V , \(L\)=1.0 mH . Параллельно LC поставьте резистор 6.2 kΩ , чтобы получить добротность \(Q\)=10 ( это даёт ширину полосы 10% , см. §1.7.14.A ). Используйте развязывающий конденсатор на входе.
==99
23 Важная зависимость \(I_S\) от температуры прямо обозначена как «\(I_S(T)\)». <-
24 J. J. Ebers & J. L. Moll, “Large-signal behavior of junction transistors”, Proc. IRE 42, 1761 ( 1954 ). <-
25 Эту картинку иногда называют графиком Гаммеля ( Gummel). <-
26 Член «25» здесь и далее на самом деле равен 25.3 mV - значению выражения \(kT/q\) при комнатной температуре. Она пропорциональна абсолютной температуре. В инженерной среде данный факт обозначается аббревиатурой “PTAT” ( читается «pee'-tat» ). Данная величина имеет интересные и полезные следствия, например, возможность создания «кремниевого термометра». Тема развивается в Части _9 и X2 . <-
27 Удобно запомнить, что \( r_e\)=25 Ω при токе коллектора 1 mA , и масштабировать на другие значения токов, например, \( r_e\)=2.5 Ω при \(I_C\)=10 mA и т.д. <-
28 На следующем уровне детализации становится понятно, что величина \( r_e\) пропорциональна абсолютной температуре, следовательно, усилитель с заземлённым эмиттером, имеющий PTAT ток коллектора, имеет крутизну ( и усиление ), которые от температуры не зависят. См. Часть X2 . <-
29 J. M. Early, “Effects of space-charge layer widening in junction transistors”, Proc. IRE 40, 1401 ( 1952 ). Джеймс Эрли ( James Early ) умер в 2004. <-
30 Зависимость между \(η\) и напряжением Эрли выражается соотношением \(η = V_T( V_A+V_{CE}) ≈ V_T/V_A\) , см. Часть X2 [* ##§X2.5 ]. <-
31
Некоторые выводы оттуда. Эффект Эрли определяет
(a) выходное сопротивление коллектора \( r_o=V_A/I_C;\)
(b) ограничивает усиление по напряжению одного каскада;
(c) ограничивает выходное сопротивление источника тока;
(d) у pnp транзисторов, как и у транзисторов с большой величиной бета, напряжение Эрли ниже, а у высоковольтных транзисторов оно выше при меньшем усилении.
Все эти выводы можно сделать, глядя на цифры \( V_A\) в табл. 8.1 .
<-
32 Программа компьютерного моделирования SPICE учитывает формулы Эберса-Молла и зарядовую модель Гаммеля-Пона. Собирать и запускать схемы на экране очень интересно. Детали раскрываются в описании моделирования искажений биполярного транзистора в SPICE в Части X2 [* §X2.4 ] . <-
33 Если посмотреть внимательнее, можно заметить ещё кое-что. На высоких частотах ( выше \( f_T/β\) ) действующее усиление по току падает обратно пропорционально с частотой. Выглядит это как линейный рост выходного импеданса эмиттерного повторителя, на который подаётся сигнал с низким \(R_S\) . Т.е. импеданс имеет индуктивный характер, и емкостная нагрузка может вызвать звон и даже генерацию Такое поведение разбирается в Части X2 . <-
34 Или, что одно и то же, когда эмиттерный резистор шунтируется конденсатором, чей импеданс на частоте сигнала сравним или меньше \( r_e\) . <-
35 Такая оценка усиления и входного импеданса будет достаточно хороша до тех пор, пока речь не идёт о высоких частотах или схемах с «активной нагрузкой», в которых коллекторный резистор заменён источником тока ( \(R_C → ∞\) ) . Общий коэффициент передачи по напряжению усилителя с заземлённым эмиттером в последнем случае ограничивается эффектом Эрли, см. обсуждение в Части X2 [* ##§X2.5 ]. <-
36 Т.к. усиление ( т.е. наклон \( V_{out}\) по отношению к наклону \( V_{in}\) ) пропорционально расстоянию до уровня \( V_{CC}\) , график на самом деле соответствует экспоненте. <-
37 Как скоро будет ясно, выходной импеданс снизится ( что полезно для усилителя напряжения ), если обратную связь брать прямо с коллектора. <-
38 R. Widlar, “Some circuit design techniques for linear integrated circuits”, IEEE Trans. Circuit Theory CT-12, 586 ( 1965 ). См. также US Patent 3,364,434. <-
39 Предупреждение . Каскадированные RC секции ( 33 kΩ + 10 μF + 33 kΩ + входной конденсатор ) вызывают появление выбросов и нестабильности и требуют внимания и аккуратности. Возможно, стоит отказаться от повторяющихся номиналов в RC цепях и от одинаковых постоянных времени. <-
40 Максимальное усиление ограничено конечным выходным сопротивлением коллектора [* в источнике тока ] - следствие эффекта Эрли. См обсуждение темы в Части X2 [* ##§X2.5 ]. <-

