10.3 Комбинационная логика

==722

В §10.1.4.A уже говорилось, что логика делится на комбинационную ( иногда называемую комбинаторной ) и последовательного действия . В комбинационных схемах выход зависит некоторым определённым образом только от текущего состояния входов, а в логике последовательного действия в формировании выхода кроме входов участвуют данные о предыдущих состояниях. Комбинационные схемы можно собрать из одних только логических вентилей, а последовательные требуется элемент памяти ( триггер ). В данной главе будут рассматриваться возможности только комбинационной логики, чтобы подготовить читателя к погружению в бурные воды схем последовательного действия.

Табл. 10.4 Логические тождества \[ \begin {align} ABC &= (AB)C = A(BC) \\ AB &= BA \\ AA &= A \\ A1 &= A \\ A0 &= 0 \\ A(B+C) &= AB+AC \\ A+AB &= A \\ A+BC &= (A+B)(A+C) \\ A+B+C &= (A+B)+C = A+(B+C) \\ A+B &= B+A \\ A+A &= A \\ A+1 &= 1 \\ A+0 &= A \\ \bar 1 &= 0 \\ \bar 0 &= 1 \\ A+\bar A &= 1 \\ A\bar A &= 0 \\ \overline{(\overline A)} &= A \\ A+\overline AB &= A+B \\ \overline{(A+B)} &= (\overline A \overline + \overline B) = \overline A ·\overline B \\ \overline{(AB)} &= \overline A+\overline B \end {align} \]

10.3.1 Логические тождества

Разговор о комбинационной логике невозможен без набора правил, перечисленных в табл. 10.4 . Большинство их очевидны, а два последних относятся к теореме ДеМоргана - самой важной для разработчика.

10.3.1.A Пример: элемент «ИСКЛЮЧАЮЩЕЕ-ИЛИ»

Проиллюстрируем показанные логические правила примером. Создадим функцию «ИСКЛЮЧАЮЩЕЕ-ИЛИ» ( «XOR» ) из обычных вентилей. На рис. 10.33 приведена таблица истинности этой функции. Из таблицы ясно, что выход принимает единичное состояние, если (A,B)=(0,1) или (1,0). Значит, можно записать

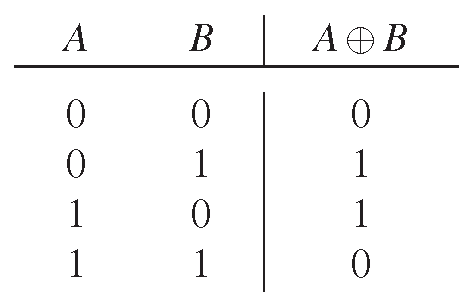
Рис. 10.33   Таблица истинности функции «ИСКЛЮЧАЮЩЕЕ-ИЛИ»

\[ A ⊕ B = \bar AB + A\bar B , \]

откуда вытекает схема 10.34 . Она не единственно возможная. Применяя логические правила можно обнаружить, что:

==723

\[ \begin {align} A ⊕ B &= A\bar A+A\bar B + B\bar A + B\bar B \qquad (A\bar A = B\bar B = 0) \\ &= A (\bar A + \bar B)+B(\bar A + \bar B) \\ &= A (\overline{AB})+B(\overline{AB}) \\ &= (A + B)(\overline{AB}) . \end {align} \]

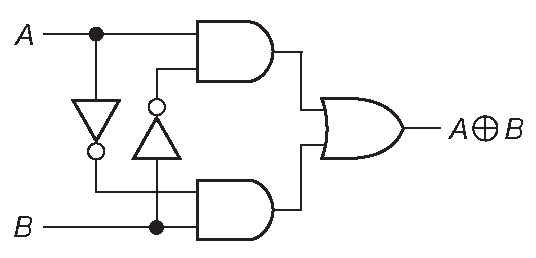
Рис. 10.34   Реализация функции «ИСКЛЮЧАЮЩЕЕ-ИЛИ»

На первом шаге к уравнению были добавлены два нулевых члена, а на третьем использовалась теорема ДеМоргана. Результат можно видеть на рис. 10.35 . Есть и другие пути реализации «ИСКЛЮЧАЮЩЕГО-ИЛИ». Разберитесь с парой упражнений.

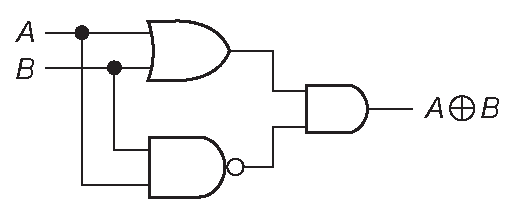
Рис. 10.35   Альтернативная реализация «ИСКЛЮЧАЮЩЕГО-ИЛИ»

Упражнение 10.12
С помощью логических преобразований покажите, что:
\( A ⊕ B = \overline{AB + \bar A\bar B}\) ,
\( A ⊕ B = (A + B)(\bar A + \bar B) .\)
Вы должны проверить результат, выписав таблицу истинности и разрисовав временнУю диаграмму состояний.

Упражнение 10.13
Упростите следующие выражения:
(a) \( 0·1 \) , (b) \( 0+1 \) , (c) \( 1·1 \) , (d) \( 1+1 \) , (e) \(A(A+B)\) , (f) \(A(\bar A+B) \) , (g) \( A⊕A \) , (h) \(A⊕\bar A \) ?

10.3.2 Минимизация логики и карты Карно

Из-за того, что логические функции могут быть реализованы несколькими способами ( даже столь простые, как «ИСКЛЮЧАЮЩЕЕ-ИЛИ» ), желательно иметь возможность отыскать самый простой или самый удобный для воплощения способ реализации конкретного логического уравнения. Над этой задачей трудились многие выдающиеся умы, которые предложили несколько способов решения, включая алгебраические методы, широко применяющиеся в программных реализациях. Скажем, все языки описания аппаратуры ( HDL ) используемые для задания функций в программируемой логике ( §11.2.6 ), содержат алгоритмы минимизации логических выражений в прозрачном для пользователя режиме.

Вы могли слышать о картах Карно ( Karnaugh ) - табличном способе минимизации логики с четырьмя или меньшим числом переменных. [* Сам способ не содержит в себе ограничений, но для более чем четырёх переменных становится достаточно громоздким, причём сложность растёт в геометрической прогрессии ] . Он же позволяет перевести таблицу истинности в логическое уравнение ( если оно вам не известно ).

Из методологических побуждений проиллюстрируем метод примером ( и никогда больше не будем использовать ). Предположим, требуется создать логическую схему, отражающую состояние большинства активных входов. Пусть имеется три входа с активными высокими уровнями, могущих принимать состояние 0 и 1 , и один выход. Выход должен переходить в состояние 1 , если как минимум два любых входа имеют состояние 1 .

Шаг 1 Строится таблица истинности

В ней должны быть отражены все возможные сочетания входов [* обозначения по краям карты ( рис. 10.36 ) ] и соответствующий выход [* цифры на поле карты] . Если подходят оба состояния [* т.е. для данного сочетания входов выход может быть и нулём, и единицей ] , в таблицу заносится «X» ( «не имеет значения» )

Шаг 2 Расписывается карта Карно

Она похожа на таблицу истинности, но переменные располагаются по двум осям. Кроме того, они организуются определённым образом: при перемещении вдоль любой из осей на каждом шаге должна меняться только одна из входных переменных ( рис. 10.36 ) [* заодно можно код Грея вспомнить, см. §10.1.3.E . Для первой слева колонки (A,B) = (0,0), т.е. A=0 , B=0 . Для второй слева - (A,B) = (0,1), т.е. A=0 , B=1 , и т.д. ] .

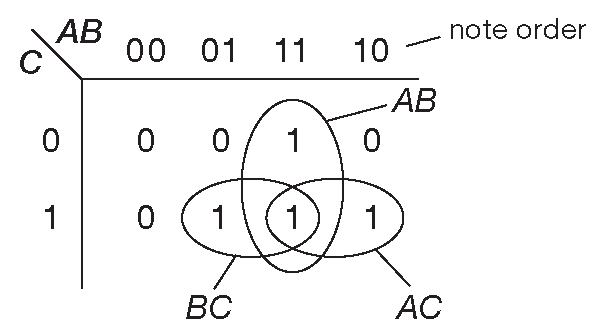
Рис. 10.36   Карта Карно для мажоритарного элемента

==724

Шаг 3 Выделение групп

На получившейся карте обводятся группы соседних единиц ( или нулей ) [*, но надо выбрать что-то одно. И не забываем об «X»: он работает как джокер и может принимать любое удобное значение ] . Наконец, записывается логическое уравнение.

[* Здесь надо поступать следующим образом. В группе одинаковых выходных состояний как минимум одна переменная не меняет своего значения ( мы специально расписывали переменные в соответствии с кодом Грея ) и одинакова для двух ( или более ) соседних ячеек на карте. Скажем, самая левая и соседняя с ней в верхнем ряду на рис. 10.36 содержат нули, т.е., подходят для объединения, и у обеих в одном состоянии находятся переменная C , потому что она определяет ряд, и переменная A . Обе равны нулю, а переменная B для интересующих ячеек меняет состояние с 0 на 1 . Поэтому здесь можно записать \( \overline{AC} \) . Ну, или для диагонального угла - две единицы на карте ( обведены овалом ). Для них A=1 , C=1 , а B меняет состояние. Пишем \( AC \). И так далее для всех возможных соседних ячеек. Учтите, что границ ( право-лево, верх-низ ) у карты нет, и поэтому крайний правый нуль в верхнем ряду должен объединяться с крайним левым нулём в том же ряду. Для них общей переменной является B , которая имеет нулевое значение, значит, пишем терм \( \overline{BC} \). Объединяться могут только 2, 4, 8 , и т.д. соседних ячеек. Можно по прямой, можно квадратами, можно прямоугольниками ( если, например, 8 ячеек ). Нельзя по диагонали, с пропуском или не по степеням двух. В верхнем ряду на карте ( рис. 10.36 ) три нуля подряд ( считая с крайнего правого ), а объединять можно только 2 или 4 , значит, получаем две группы с двумя переменными в каждой. Выписывать термы уравнения надо для какого-то одного состояния выхода Q=0 ( /Q ) или Q=1 ( Q ) ] .

Таким образом, получаем \[ Q = AB + AC + BC \]

Схемная реализация показана на рис. 10.37 . В конце процесса результат кажется очевидным. Можно записать уравнение и для групп нулей:

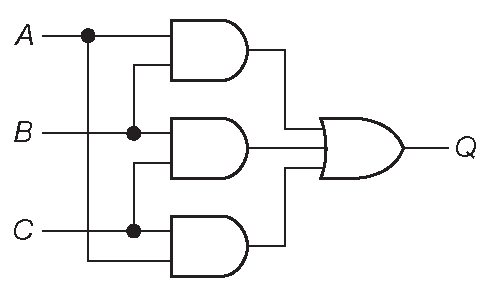
Рис. 10.37   Мажоритарный элемент

\[ \overline{Q} = \overline{AB} + \overline{AC} + \overline{BC} . \]

Эта форма может быть удобна, если в схеме уже есть дополнения входных переменных.

Упражнение 10.14
Нарисуйте карту Карно для функции, которая показывает, что 3-разрядное двоичное число является простым ( считать, что 0, 1 и 2 к простым не относятся ). Нарисуйте схему для 2-входовых вентилей.

Упражнение 10.15
Нарисуйте карту Карно для схемы умножения двух 2-разрядных беззнаковых двоичных чисел ( т.е. каждое может принимать значения от 0 до 3 ) с получением 4-разрядного результата.
Подсказка используйте отдельную карту для каждого разряда результата.

10.3.3 Комбинационные функции, доступные в виде ИМС

На простых логических вентилях можно построить достаточно сложные логические функции: сложение, сравнение, контроль чётности, мультиплексирование ( выбор конкретного входа из имеющегося набора в соответствии с состоянием адресных битов [* рис. 10.29 ] ) и т.д. Именно это происходит при построении логической схемы в вентильной матрице ³⁹ или иной микросхеме программируемой логики ( см. §10.3.3.F , §10.5.4 и Часть 11 ). Программируемая логика ( часто дополняемая микроконтроллером ) - самый естественный выбор для построения цифрового или аналого-цифрового устройства. Именно этот путь будет показан в следующих частях.

Все эти функции доступны в виде микросхем средней степени интеграции ( до 100 вентилей ) как элементы стандартной логики. Хотя основная часть таких микросхем построена с использованием триггеров ( т.е. являются схемами последовательного действия, до которых скоро дойдёт дело ), есть и некоторые чисто комбинационные, состоящие только из логических вентилей. Посмотрим на этот зоопарк поближе.

10.3.3.A 2-входовой селектор ( мультиплексор )

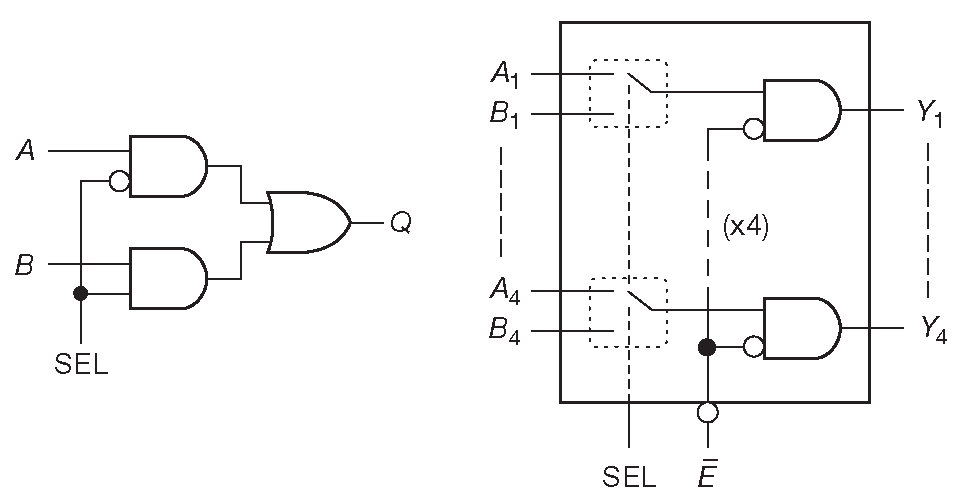
Рис. 10.38     2-входовой селектор. (A) Реализация на отдельных логических элементах и (B) в виде счётверённой ИМС с общими линиями выбора «SEL» и разрешения «/E»

2-входовая схема выбора ( называемая также мультиплексором или «MUX» ) очень полезная функция. Исходно это переключатель на два направления для логических сигналов. Рис. 10.38 знакомит с базовой идеей в виде реализации на отдельных вентилях и в форме специальной ИМС, в которую умещается четыре 2-входовых селектора ( «счетверённый мультиплексор» ). Когда на входе «SELECT» НИЗКИЙ уровень, на выход «Y» проходит информация со входа «A», а при ВЫСОКОМ активен канал «B». Подача на «/ENABLE» ВЫСОКОГО уровня запрещает работу, переводя все выходы в НИЗКОЕ состояние. Это очень важная возможность, которая будет разобрана чуть позднее. Вот таблица истинности 2-входового селектора, где «X» означает «любой логический уровень»

    /E  S   An  Bn  Yn
    H   X   X   X   L
    L   L   L   X   L
    L   L   H   X   H
    L   H   X   L   L
    L   H   X   H   H 

Она может быть переписана компактнее:

    /E  S   Yn
    H   X   L
    L   L   An
    L   H   Bn 

В языках описания аппаратуры 2-входовой селектор без входа «ENABLE» описывается так: Y = ~S & A | S & B; , а с «ENABLE»: Y = E & ( ~S & A | S & B ) ⁴⁰ . На рис. 10.38 и в таблице истинности выше описан элемент ’157. Та же функция, но с инверсным выходом имеет номер ’158, а пара ’267 и ’268 имеет выходы с третьим состоянием. Есть компактные реализации в виде одно- и двухканальных переключателей без входа «ENABLE» с номерами ’1G157 и ’2G157. Описанные микросхемы являются логическими вентилями, т.е. они переключают свои состояния в соответствии со входными сигналами, воспроизводя нужные логические уровни на выходах. Есть ещё один способ решения данной задачи - использовать переключаемые каналы передачи , по которым нужные сигналы просто проходят от входа к выходу ( через проводящий канал МОП транзистора ). Такие микросхемы входной сигнал не воспроизводят . Разговор о них впереди.

==725

Упражнение 10.16
Изобразите 2-входовой селектор, используя пару элементов с третьим состоянием и дополнительную логику по собственному выбору.

Селектор можно собрать на механических переключателях, но электронный вариант гораздо лучше по нескольким причинам.

1. Он дешевле.
2. Все каналы переключаются быстро и одновременно.
3. Его можно мгновенно переключить сигналом, сформированным в другой части схемы ( или каким-нибудь интеллектуальным устройством вроде микропроцессора ).
4. Даже если управляющий сигнал идёт с механического ключа на передней панели, сами переключаемые сигналы не гоняются до панели и обратно, не ослабляются на контактах и не набирают внешний шум.

Электронный переключатель, активируемый постоянным напряжением, позволяет удерживать информационные каналы в пределах печатной платы и упрощает соединение с внешним миром: потребуется один провод с подтяжкой, замыкаемый на землю одним выключателем ( SPST ). Управление работой устройства с помощью постоянных напряжений с уровнями логики называется «холодным переключением», и это гораздо более удобный способ, нежели работа с самими сигналами с помощью переключателей, потенциометров и т.д. Помимо прочих удобств линии холодного управления можно снабжать фильтрующими конденсаторами, убирающими наводки, а с сигнальными шинами так поступать нельзя. Некоторые примеры холодного управления будут показаны позже.

10.3.3.B Проводящие элементы

Как сообщалось в §3.4.1.A технология КМОП позволяет создавать проводящие элементы - пару параллельных МОП ключей. Такие ключи либо передают напряжение в виде аналогового сигнала в диапазоне от земли до \( V_{DD} \) сквозь низкоомный ( менее 100 Ω ) проводящий канал, либо разрывают соединение ( увеличивают сопротивление канала практически до бесконечности ). Ключи получаются двунаправленными и «не знают», какой из концов является входом, а какой - выходом. Проводящие элементы хорошо работают с обычными логическими КМОП сигналами и фактически активно используются внутри цифровых КМОП схем. Они предлагаются и в виде стандартных ИМС. На рис. 10.39 показана структура популярного КМОП элемента ’4066 – «счетверённого двунаправленного ключа». Каждый канал имеет индивидуальную линию управления : ВЫСОКИЙ уровень разрывает соединение, а НИЗКИЙ замыкает его. Есть и компактные одно- двухсекционные варианты ( ’1G66 и ’2G66 ). Следует подчеркнуть, данные элементы - просто ключи, и к ним не применим параметр «коэффициент разветвления» . Они просто передают напряжение на выход, не обеспечивая его дополнительной мощностью ⁴¹ . [* Т.е. источник сигнала получает всю нагрузку на выходе микросхемы плюс последовательное сопротивление канала ] .

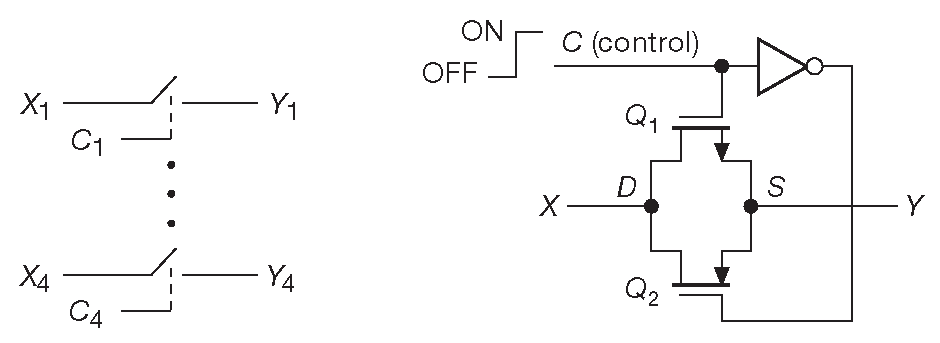
Рис. 10.39   Счетверённый переключатель на проводящих элементах. Справа один канал, собранный на МОП транзисторах

Электронные ключи позволяют строить 2-входовой ( или сколько там требуется? ) селектор, который сможет работать с логическими уровнями КМОП или аналоговыми напряжениями. Надо просто набрать ключей по числу каналов и управлять ими с помощью декодера , как будет показано далее. В итоге получилась столь популярная логическая функция, что она получила даже собственное имя – «мультиплексор» .

Упражнение 10.17
Покажите, как построить 2-входовой селектор на ключах. Потребуется инвертор.

10.3.3.C Многовходовые мультиплексоры

Мультиплексоры бывают на 2, 4, 8 и 16 входов. Для выбора конкретного входного сигнала используется двоичный адресный код. Скажем, 8-входовой мультиплексор имеет 3 адресные линии выбора канала ( рис. 10.40 ), носит номер ’151, снабжён входным активным низким стробом ( «/STROBE» или «/ENABLE» ) и комплементарными выходами «Y» и «/Y». В запрещённом состоянии ( на «/ENABLE» подан ВЫСОКИЙ уровень ) «Y» находится в НИЗКОМ состоянии, а «/Y» - в ВЫСОКОМ, независимо от состояния всех прочих входов.

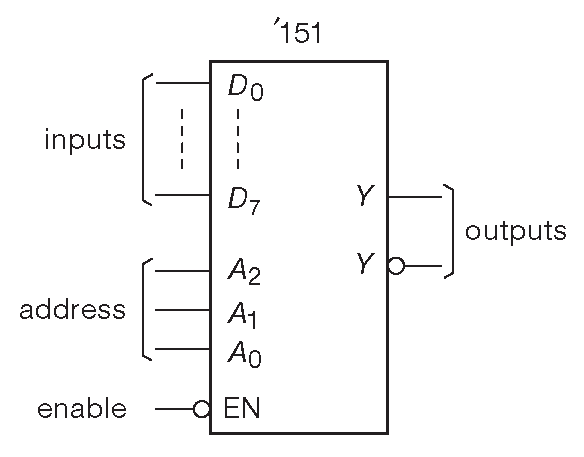
Рис. 10.40   Элемент ’151 - 8-входовой мультиплексор

==726

Полезно познакомиться с тем, как на языках описания аппаратуры осуществляется ввод логических схем, просто для общего развития. Рис. 10.41 представляет описание для чуть более простого 4-входового мультиплексора.

wire[1:0] A;                  //2 address ("select") input lines
wire[3:0] D;                  //4 input data lines
wire Y, YBAR, ENBAR;          // outputs (true and complemented), and enable

assign Y = ~ENBAR & ( D[0] & ~A[1] & ~A[0]
                    | D[1] & ~A[1] &  A[0]
                    | D[2] &  A[1] & ~A[0]
                    | D[3] &  A[1] &  A[0] );
assign YBAR = ~Y; 

Существуют два вида мультиплексоров. Один - только для цифровых сигналов, с порогом переключения на входе и воспроизведением правильных логических уровней на выходе. Пример: ’153 - логический мультиплексор, присутствующий и в биполярных, и в КМОП семействах. Другим вариантом мультиплексоров являются аналоговые двунаправленные схемы, собранные на электронных ключах. Такие мультиплексоры бывают только в КМОП исполнении и могут использоваться для коммутации аналоговых и цифровых сигналов. Так работают элементы ’4051-’4053. Не забывайте, что такие ключи не имеют коэффициента разветвления. Двунаправленная природа этих ИМС позволяет использовать их в качестве «демультиплексоров» или декодеров.

Упражнение 10.18
Покажите, как построить 4-входовой мультиплексор на
(a) обычных вентилях, (b) элементах с третьим состоянием, (c) электронных ключах.
В каком случае предпочтителен последний вариант?

Возникает вопрос, что делать, если требуется переключать больше линий, чем позволяют обычные мультиплексоры? Это тема из категории «проблем масштабирования» : как из нескольких микросхем с ограниченными возможностями собрать систему с расширенным функционалом. Он применим к декодерам, мультиплексорам, сдвиговым регистрам, арифметическим устройствам и вообще любой логической функции. В данном случае решение затруднений не вызывает ( рис. 10.42 ). В примере два 8-входовых мультиплексора 74LS151 были объединены для получения 16-входового варианта. Обратите внимание, что для маркировки сигналов используются строчные буквы, чтобы не путать их с одноимёнными входами микросхем ⁴² . Появляется дополнительный разряд адреса, который используется для выбора одной или другой микросхемы. В запрещённом состоянии выход «Y» имеем НИЗКИЙ уровень, поэтому для объединения используется вентиль «ИЛИ». Для элементов с третьим состоянием работа была бы проще, потому что входы можно было бы просто объединить.

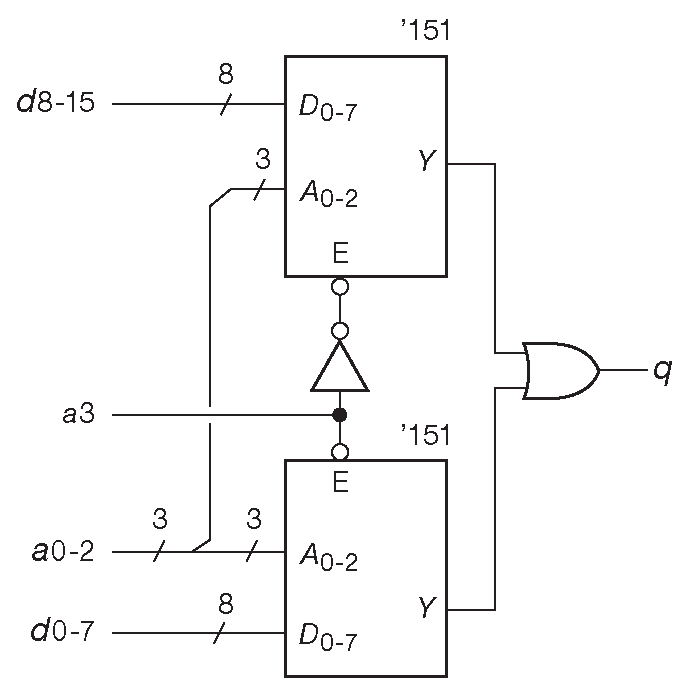
Рис. 10.42   Увеличение разрядности мультиплексоров

10.3.3.D Декодеры и демультиплексоры

==727

Демультиплексоры выполняют «обратное мультиплексирование». Они принимают на входе один сигнал и перенаправляют его на один из выходов, выбираемый согласно состоянию адресных линий. На остальных выходах может присутствовать неактивный уровень или состояние обрыва в зависимости от типа демультиплексора.

Декодеры работают аналогично, за исключением того, что на входе имеются только адресные линии, которые переводят один из n выходов в активное состояние. На рис. 10.43 показан пример. Это элемент ’138 - декодер «1-в-8». На выходе, чей номер совпадает с сочетанием уровней на адресных входах, появляется НИЗКИЙ уровень, а на всех остальных - пассивный ВЫСОКИЙ. Данный элемент имеет целых три входа «ENABLE», каждый из которых должен быть переведён в разрешающее состояние, в противном случае все выходы будут иметь ВЫСОКИЙ уровень.

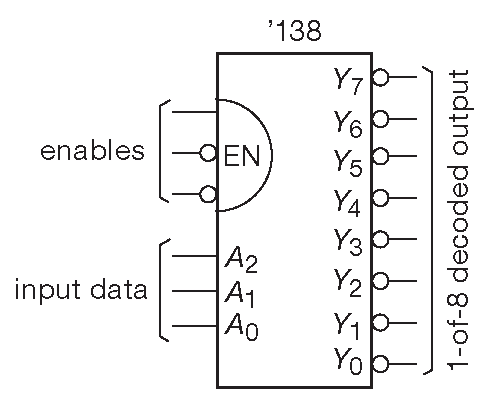
Рис. 10.43   Элемент ’138 - декодер 1-в-8

Декодеры обычно используют для подключения к шине данных. Эта тема подробно разбирается в Части 14 . Ещё одним вариантом использования является выбор разных действий для разного сочетания уровней на адресных линиях. Адрес при этом приходит с выхода двоичного счётчика ( §10.4.2.E ). Близким родственником элемента ’138 является ’139 - сдвоенный декодер «1-в-4» с одним индивидуальным активным низким входом «/ENABLE» на секцию и общими адресными входами. На рис. 10.44 показано, как его можно описать на Verilog.

wire [1:0] A;             // 2-bit adress: brackets show array range
wire [3:0] YBAR;          // four active-LOW outputs
wire ENBAR;               // active-LOW enable

assign YBAR[0] = ~( ~ENBAR & ~A[1] & ~A[0] );
assign YBAR[1] = ~( ~ENBAR & ~A[1] &  A[0] );
assign YBAR[2] = ~( ~ENBAR &  A[1] & ~A[0] );
assign YBAR[3] = ~( ~ENBAR &  A[1] &  A[0] ); 

На рис. 10.45 показано, как из двух ’138 сделать декодер «1-в-16». ИМС имеет входы «ENABLE» обеих полярностей, поэтому дополнительные вентили здесь не нужны.

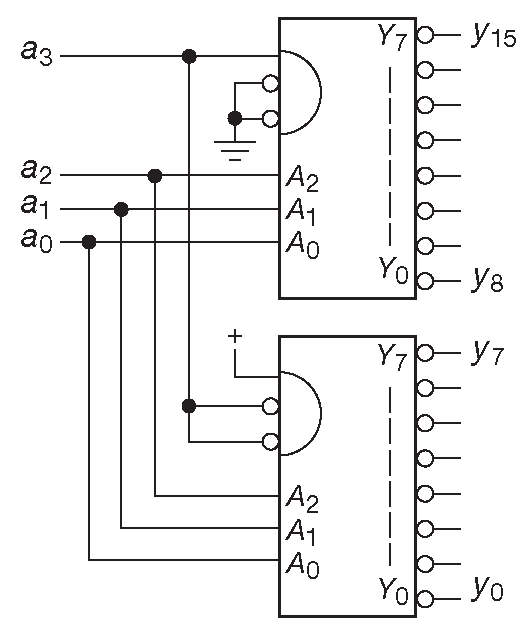
Рис. 10.45   Расширение разрядности декодера

Упражнение 10.19
Расширьте схему 10.45 до уровня «1-в-64».
Подсказка один из ’138 можно использовать для выбора других.

В КМОП логике мультиплексоры, основанные на проводящих элементах, могут с успехом служить демультиплексорами, т.к. исходно являются двунаправленными схемами. Если они используются именно так, то неактивные выходы находятся в оборванном состоянии, о чём надо помнить. Подтяжки на землю или питание либо иное схемное решение должно задавать неактивный логический уровень на таких линиях. Это же требование относится и к биполярным выходам с открытым коллектором.

Ещё один вид декодеров представлен элементом ’47 - драйвером/декодером «BCD в 7-сегментный код». Он получает на входе число в двоично-десятичной кодировке и выставляет на 7 выходных линиях сигналы для управления 7-сегментным индикатором. Этот декодер является примером преобразователя кодов, но общепринятой практикой является использование термина «декодер».

Упражнение 10.20
Разработайте декодер «1-в-10», используя обычные вентили.

Упражнение 10.21
Придумайте шифратор - схему, которая будет выдавать 2-разрядный двоичный код и сообщать, какой из 4 её входов находится в ВЫСОКОМ состоянии ( остальные должны иметь НИЗКИЙ уровень ).

Упражнение 10.22
Покажите, как можно построить генератор чётности на элементах «ИСКЛЮЧАЮЩЕЕ-ИЛИ».

10.3.3.E Арифметические схемы

Приоритетный шифратор выдаёт двоичный код, соответствующий активированному входу с самым большим номером. Он удобен для использования в АЦП с параллельным преобразованием ( см. Часть 13 ) и в микропроцессорных системах. Примерами являются элементы ’148 на 8 входов и ’147 на 10 входов.

==728

На рис. 10.46 показан 4-разрядная схема сравнения или компаратор . Она оценивает два входных 4-разрядных числа A и B и сообщает результат, устанавливая три выхода «A<B», «A=B» и «A>B». Имеются и три соответствующих входа для наращивания разрядности.

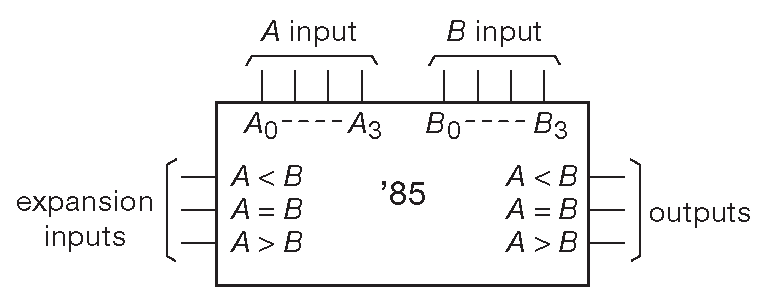
Рис. 10.46   Цифровой компаратор

Схема проверки на чётность используется для генерации бита чётности, который можно добавить к «слову» данных при передаче или записи, а при приёме или чтении проверить. Проверять можно чётность или нечётность ( при нечётности число единиц в каждом информационном слове [* включая сам бит чётности ] нечётное ). Элемент ’280, выполняющий такую функцию принимает на входе 9-разрядное слово и выдаёт бит чётности и нечётности. Такие схемы делаются на элементах «ИСКЛЮЧАЮЩЕЕ-ИЛИ».

На рис. 10.47 показан 4-разрядный полный сумматор ⁴³ . Он складывает 4-битное слово A_i , 4-битное слово B_i и входной бит переноса C_i с получением 4-битной же суммы S_i и выходного бита переноса C_o . Входной и выходной перенос позволяют наращивать разрядность. Для этого выход переноса C_o сумматора младших разрядов должен заводиться на вход переноса C_i ближайшего старшего сумматора.

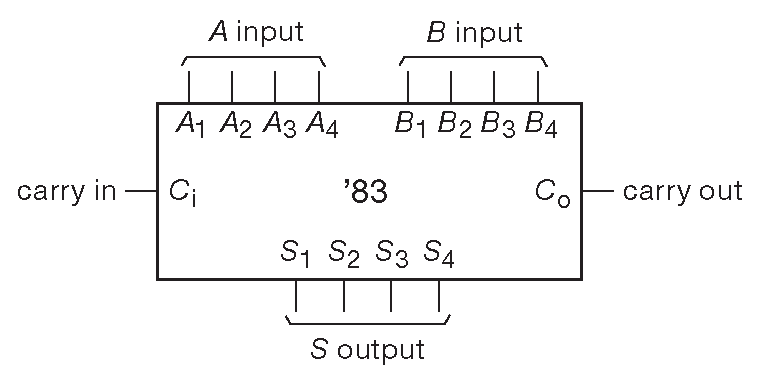
Рис. 10.47     4-разрядный полный сумматор

На рис. 10.48 показано описание 4-разрядного сумматора на Verilog. Теперь оно дано в более полной форме для большей ясности. Попробуйте разобраться, как получается итоговая сумма.

wire [3:0] A;
wire [3:0] B;
wire [3:0] S;                      // sum bits
wire CIN, COUT;                    // carries

assign S[0] = A[0] ∧ B[0] ∧ CIN;  //  recall "∧" means XOR
assign C01 = A[0] & B[0] | A[0] & CIN | B[0] & CIN;
assign S[1] = A[1] ∧ B[1] ∧ C01;
assign C12 = A[1] & B[1] | A[1] & C01 | B[1] & C01;
assign S[2] = A[2] ∧ B[2] ∧ C12;
assign C23 = A[2] & B[2] | A[2] & C12 | B[2] & C12;
assign S[3] = A[3] ∧ B[3] ∧ C23;
assign COUT = A[3] & B[3] | A[3] & C23 | B[3] & C23; 

Одним из приятных свойств языков Verilog и VHDL является задание более высокого уровня абстракции. В данном примере весь текст после объявлений «wire» можно было сократить до « assign {COUT,S} = A + B + CIN;» .

В качестве сумматора можно использовать и арифметическо-логическое устройство ( ALU ), но его возможности шире. Например, 4-разрядное АЛУ ’181 ( которое можно расширить до нужной разрядности ) может выполнять сложение, вычитание, сдвиг, сравнение и несколько логических функций. Сумматоры и АЛУ выполняют математические манипуляции за время, исчисляемое наносекундами. Конкретное время зависит от используемого семейства. Есть и другие арифметические микросхемы: умножитель с накоплением ( MAC ) ( суммирует произведения поступающих на вход слов ) и коррелятор ( сравнивает две битовые строки и сообщает число совпадающих позиций ).

В настоящий момент конструкции цифровых устройств, требующих интенсивных вычислений, опираются на мощные и быстрые микропроцессоры общего назначения или специализированные процессоры цифровой обработки сигналов ( DSP ). Ещё одним привлекательным вариантом являются программируемые вентильные матрицы ( FPGA ), которые можно сконфигурировать практически под любую задачу, включая «программный» микропроцессор, снабжённый аппаратными ускорителями для сложных математических функций. Речь о программируемой логике пойдёт в Части 11 , а о микропроцессорах - в Части 15 .

10.3.3.F Программируемые логические микросхемы

Комбинационную ( или последовательного действия ) схему можно сформировать в кристалле программируемой логики ещё одного вида - в программируемых логических устройствах ( PLD ). На данный момент наибольшей популярностью пользуются cPLD - сложные логические микросхемы, состоящие из набора макроячеек, и вентильные матрицы ( FPGA ). Оба вида быстры, универсальны и удобны в использовании. Каждый разработчик должен уметь работать с ними. Эти устройства ещё встретятся и в этой части и в Части 11 .

==728