10.1 (II) Основные принципы работы логических схем
==708
10.1.4 Логические элементы и таблицы истинности
10.1.4.A Комбинационная логика и логика последовательного действия
Цифровая электроника - это игра, в которой надо собрать цифровой выход из цифровых же входов. Например, сумматор может получить на входе два 16-разрядных слагаемых и выдать 16-разрядную сумму и бит переноса. Или можно собрать умножитель. Всё это различные виды операций, которые должно выполнять арифметическое устройство. Другой задачей является сравнение двух чисел, для выяснения, какое из них больше, или сравнение константы со входным набором битов, чтобы понять, что «всё работает, как надо». А может, нужен бит чётности, чтобы добавить его к числу и получить чётное число единиц при передаче по каналу связи. На приёмном конце чётность может быть проверена и тем самым выяснена корректность данных. Ещё одной типовой задачей служит преобразование двоичного числа в десятичную форму для последующего вывода. Это всё примеры конкретных действий, в которых выход или выходы является заданной функцией от набора входов. Их общее название - комбинационные задачи 12 . Выполняться данные действия могут с помощью «комбинационной логики» - наборов логических элементов или вентилей , выполняющих элементарные действия в двоичных системах (с двумя состояниями).
==709
Есть ещё один класс задач, который не может быть решён комбинационной логикой из одного только набора входных сигналов, но нуждается в сведениях о предыстории текущего состояния. Разрешение данного затруднения требует использования «логики последовательного действия». Типичной задачей для таких компонентов может служить преобразование параллельных данных в последовательную форму (один после другого) или сохранение числа единиц в последовательности, либо обнаружение нужного сочетания битов, выдача одного импульса на четыре входных. Все эти задачи требуют какого-то элемента памяти. Базовым элементом такого типа является триггер или «бистабильный мультивибратор».
Знакомство начнётся с комбинационной логики, потому что это основа всех остальных её видов. Тему чуть оживит появление элементов последовательного действия, но особое удовольствие от самих логических элементов получить сложно.
10.1.4.B Элемент «ИЛИ»
На выходе элемента «ИЛИ» будет ВЫСОКИЙ уровень, если хотя бы один вход будет в ВЫСОКОМ состоянии. Данное условие можно записать в виде таблицы истинности , как на рис. 10.4 , где приводится такая таблица для 2-входового элемента «ИЛИ». В общем случае входов может быть сколь угодно много, но, если ограничиться корпусом стандартной логической микросхемы, то можно выбрать между двумя и одиннадцатью входами 13 . Например, для 4-входового «ИЛИ» выход будет ВЫСОКИМ, если ВЫСОКИЙ уровень имеется на любом из четырёх входов (или на нескольких входах одновременно).
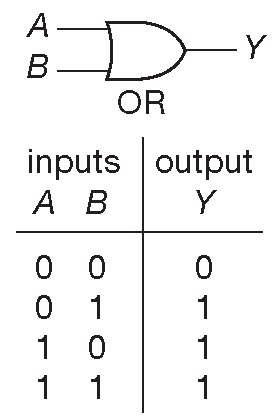
Рис. 10.4 2-входовой элемент «ИЛИ» и его таблица истинности
В булевой алгебре для операции «ИЛИ» отведён символ «+». «A ИЛИ B» записывается как «A+B» в текстовой форме или как «A|B» в формате языков Verilog и Си.
10.1.4.C Элемент «И»
Выход элемента «И» Будет ВЫСОКИМ, только если все его входы имеют ВЫСОКОЕ состояние. Логический символ и таблица истинности приведены на рис. 10.5 . Так же, как и в случае схемы «ИЛИ», вентили «И» могут иметь 2, 3, 4 и более входов. Например, 8-входовой элемент «И» переведёт выход в ВЫСОКОЕ состояние, когда ВЫСОКИЙ уровень будет на всех восьми входах.
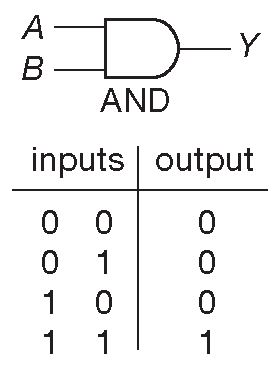
Рис. 10.5 2-входовой элемент «И» и его таблица истинности
В булевой алгебре для «И» используется символ точки (•). Он может быть опущен, и чаще всего опускается. «A И B» записывается «A•B» или просто «AB», а в Verilog или Си «A&B».
10.1.4.D Элемент «НЕ» (инвертор)
Часто требуется получить логическое дополнение некоторого состояния. Именно для этого и нужен инвертор - вентиль с одним входом и одним выходом (рис. 10.6 ).
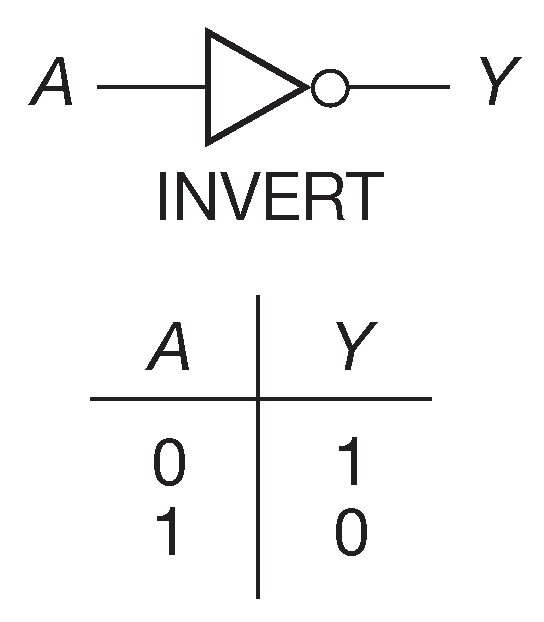
Рис. 10.6 Схемный символ инвертора и его таблица истинности
==710
В булевой алгебре операция «НЕ» обозначается горизонтальной чертой над символом, а иногда знаком ('). «НЕ A» записывается как «\(\bar{A}\)» или «\(A'\)». Для удобства набора символ горизонтальной черты может заменяться прямым слэшем (/), минусом (-) и звёздочкой (*). Таким образом, «НЕ A» может записываться в форме «A'», «—A», «*A», «/A», «A*», «A/». Для конкретного документа обычно выбирается что-то одно. В данной книге инверсию обозначает апостроф «A'» [* или слэш «/A» ] . В языках программирования используются символы «!» или «~».
Смежная тема: время распространения.
В реальном мире логические элементы не меняют состояние выхода мгновенно при изменении состояния входа. Новости добираются со входа на выход за время, называемое «временем распространения» ( \(t_{pd}\) ). На рис. 10.7 даётся реальная картина для инверторов из пяти логических семейств, на вход которых подаётся один импульс длительностью 15 ns . Самые быстрые - новые низковольтные семейства «74AUC» и «74ALVC». Они имеют задержку распространения менее 2 ns .
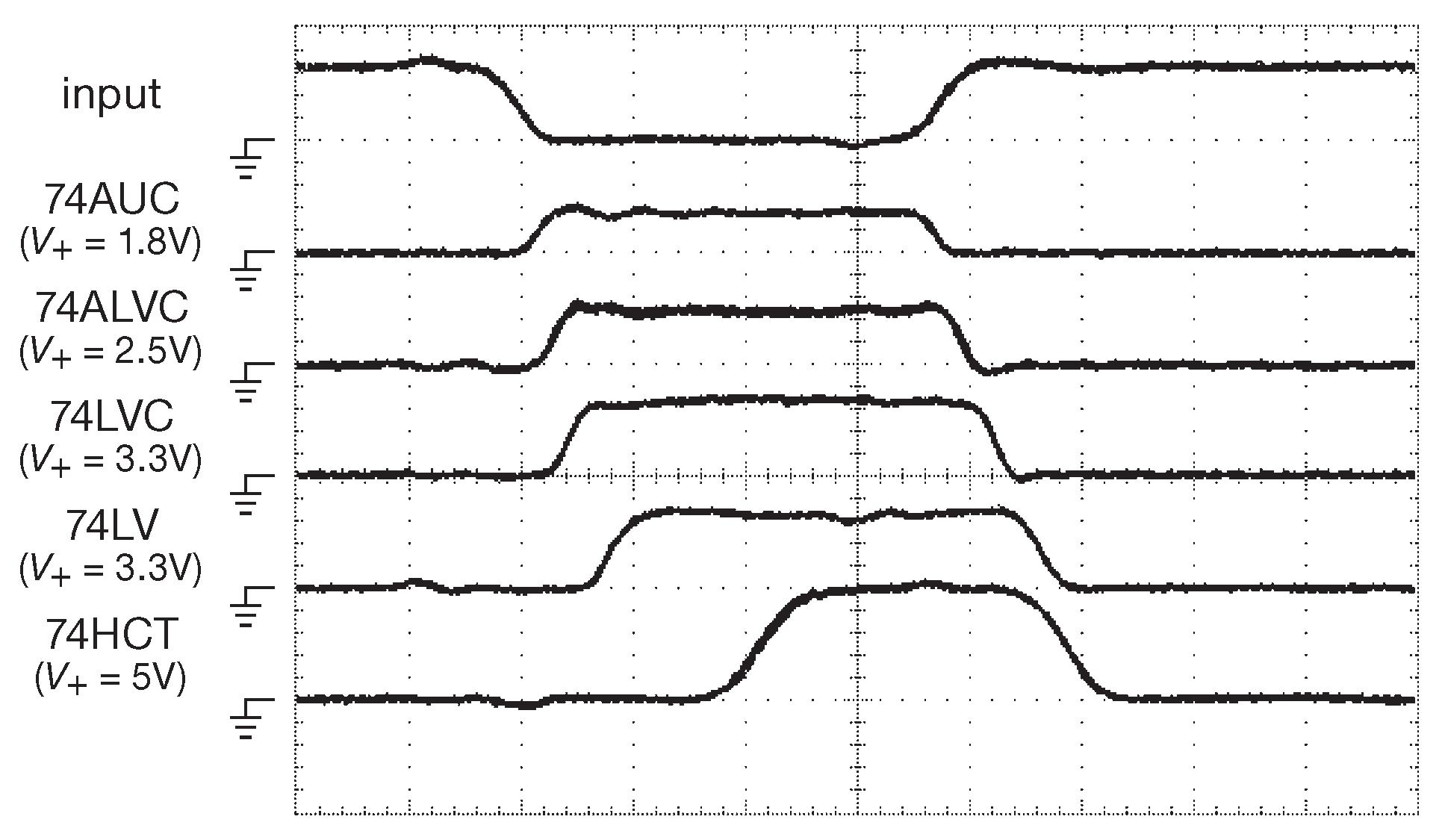
Рис. 10.7 Физическим логическим элементам требуется некоторое время, чтобы отразить изменения на входе. На входы инверторов из нескольких популярных логических семейств были поданы активные НИЗКИЕ импульсы, чтобы оценить время задержки. Самое медленное семейство ( «74HCT» на входе сигнал с размахом 5V ) показало задержку 9 ns от нисходящего ( переднего ) фронта и 5 ns от восходящего ( заднего ). В итоге у него оказался самый короткий выходной импульс. По горизонтали 4 ns/div , по вертикали 5 V/div
10.1.4.E Элементы «И-НЕ», «ИЛИ-НЕ»
Инверсия может комбинироваться с другими логическими функциями и образовывать элементы «И-НЕ» и «ИЛИ-НЕ» (рис. 10.8 ), которые популярны больше, чем простые «И/ИЛИ». Дело в том, что инверсия позволяет строить на этих элементах любую логическую функцию, о чём позднее ещё будет разговор.
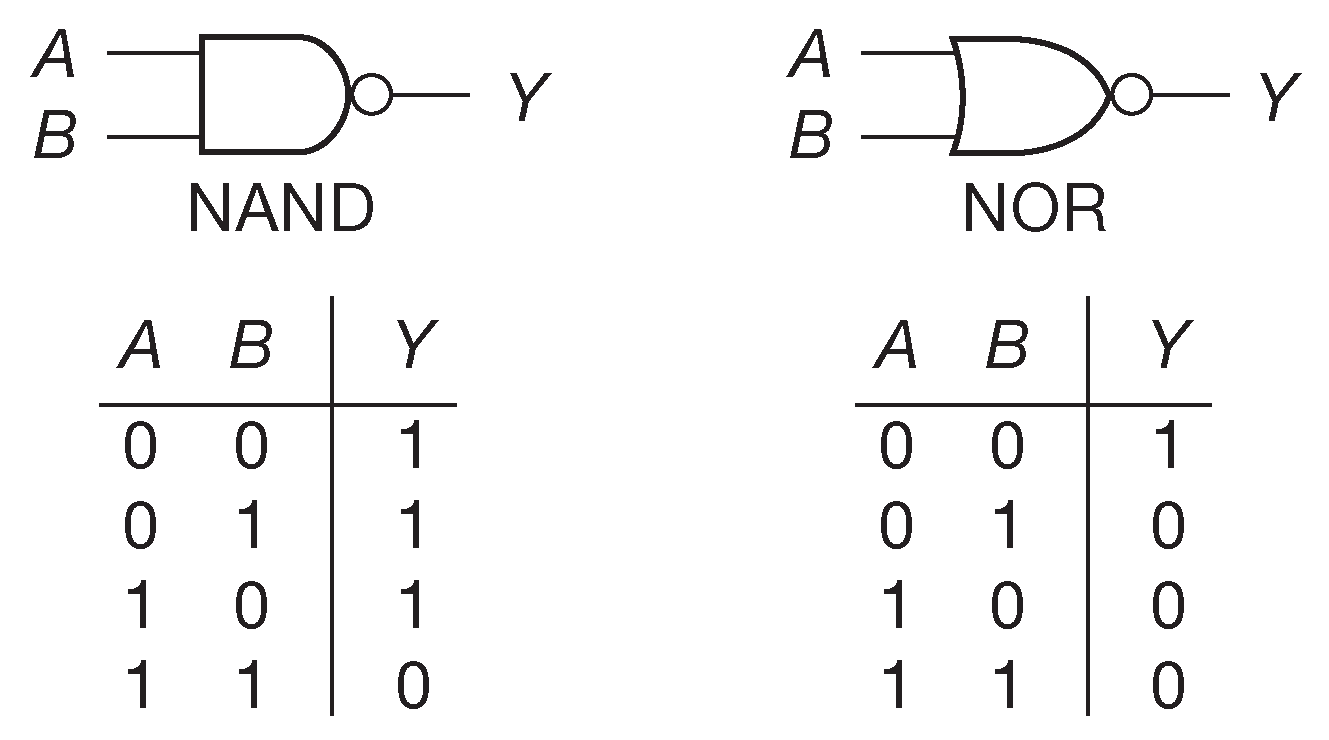
Рис. 10.8 Схемный символ «И-НЕ» и «ИЛИ-НЕ» и их таблицы истинности
10.1.4.F Элемент «ИСКЛЮЧАЮЩЕЕ-ИЛИ»
«ИСКЛЮЧАЮЩЕЕ-ИЛИ» ( XOR ) - очень интересная функция (рис. 10.9 ), хотя и не столь основополагающая, как «И» и «ИЛИ». Выход элемента «ИСКЛЮЧАЮЩЕЕ-ИЛИ» будет ВЫСОКИМ, если ВЫСОКИЙ любой из входов, но не оба вместе. Иначе говоря, выход ВЫСОКИЙ, если на входах различные состояния. У этого элемента бывает только два входа 14 . Элемент «ИСКЛЮЧАЮЩЕЕ-ИЛИ» идентичен сумматору «по-модулю-2». В булевой алгебре он имеет символ «⊕», а в языках программирования Verilog и Си обозначается знаком «⋀» 15 .
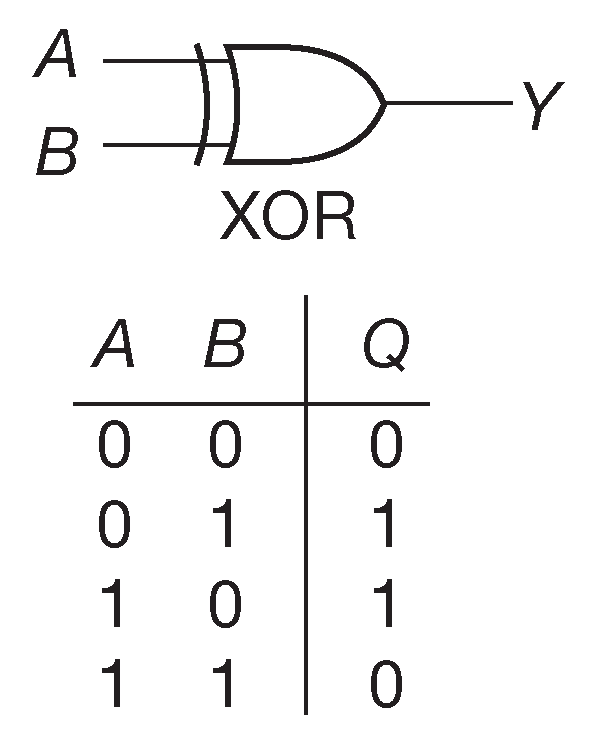
Рис. 10.9 Схемный символ «ИСКЛЮЧАЮЩЕЕ-ИЛИ» и его таблица истинности
Упражнение 10.5
Покажите, как можно использовать «ИСКЛЮЧАЮЩЕЕ-ИЛИ» в качестве «управляемого инвертора», т.е. элемента, который инвертирует сигнал или передаёт его без инверсии в зависимости от состояния управляющего вывода.
Упражнение 10.6
Покажите, что схема 10.10 преобразует двоичное представление в код Грея и обратно.
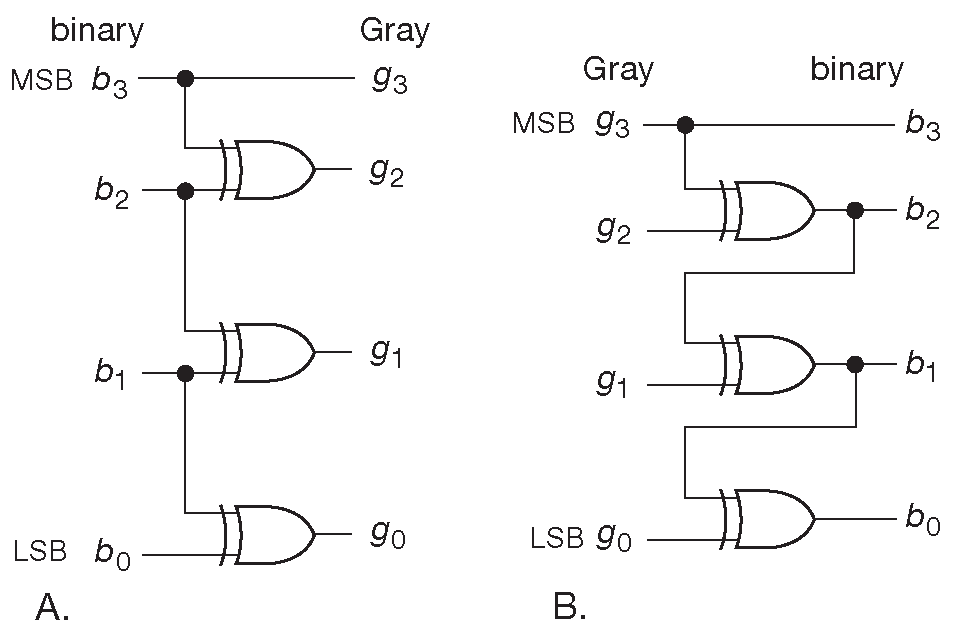
Рис. 10.10 Преобразователи параллельных кодов: двоичного в код Грея и код Грея в двоичный
==711
10.1.4.G Языки описания аппаратуры
До настоящего момента для базовых логических функций использовались графические символы . Но когда вместо цифровых микросхем малой степени интеграции используются программируемые логические микросхемы ( PLD, Часть 11 ), приходится описывать нужные логические функции текстом. Делается это с помощью языков описания аппаратуры ( HDL ). Обычно в этом качестве выступают Verilog и VHDL. Специальное программное обеспечение разбирает и преобразует текстовое описание и выдаёт файл, пригодный для загрузки в микросхему (или, если речь идёт о больших объёмах выпуска, то для изготовления заказных кристаллов). Таблица на рис. 10.11 показывает синтаксические различия в описании базовых логических операций между несколькими языками, используемыми для таких задач.
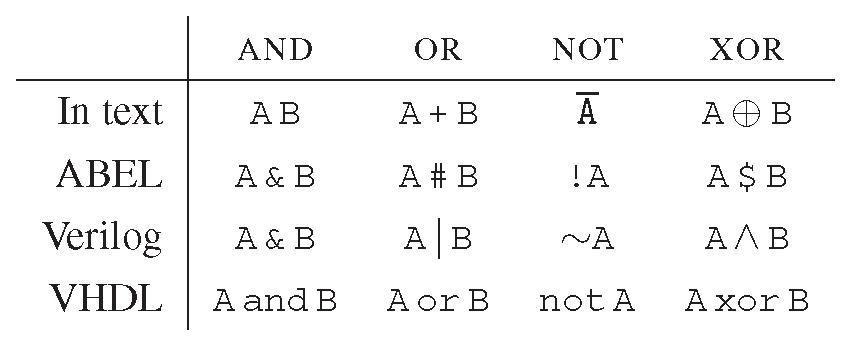
Рис. 10.11 Синтаксические различия в обозначении логических операций в исходных текстах языков описания аппаратуры и в книжном тексте. Язык CUPL использует те же обозначения, что и ABEL. Альтернативные символы для «И» «A•B», для «НЕ» - что-нибудь из списка «A'», «A*», «*A», «/A», «A/», «-A»
В качестве простого примера приведём описание схемы 10.10B , преобразующей код Грея в двоичный код на языке Verilog:
assign b3 = g3; assign b2 = g2 ⋀ g3; assign b1 = g1 ⋀ (g2 ⋀ g3); assign b0 = g0 ⋀ (g1 ⋀ (g2 ⋀ g3));
10.1.5 Схемная реализация логических элементов
Прежде чем переходить к использованию логических микросхем, посмотрим, как можно реализовать логические функции на дискретных компонентах. На рис. 10.12 показана схема элемента «И». Если какой-то из входов подключить к НИЗКОМУ уровню, то на выходе будет НИЗКИЙ уровень. Выход перейдёт в ВЫСОКОЕ состояние, только если оба входа имеют ВЫСОКИЕ уровни. Схема рабочая, но недостатков у неё много.
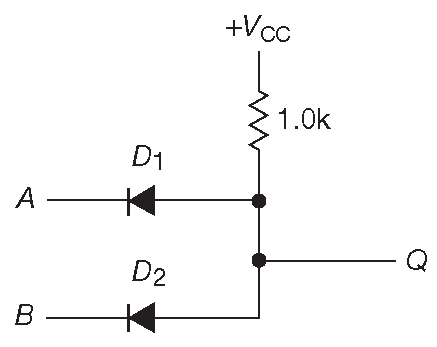
Рис. 10.12 Схема «И» на диодах
- НИЗКИЙ вЫходной уровень на одно падение на диоде выше НИЗКОГО входного уровня. Очевидно, использовать несколько таких элементов последовательно не выйдет.
- У схемы отсутствует понятние «коэффициент разветвления» ( возможность подключения нескольких входов к одному выходу ), т.к. любая нагрузка на вЫходе видна источнику сигнала на входе.
- Схема медленная, т.к. сделана на резистивной подтяжке.
Вариант 10.13 исправляет некоторые недостатки. С помощью пары ключей на npn транзисторах делается вентиль «ИЛИ-НЕ», а дополнительный инвертор позволяет получить чистое «ИЛИ» 16 . ВЫСОКИЙ уровень на одном или двух входах включает какой-то из входных транзисторов и переводит их общий выход в НИЗКОЕ состояние. Т.к. получившийся логический элемент инвертирует сигнал, на выход добавлен ещё один инвертор.
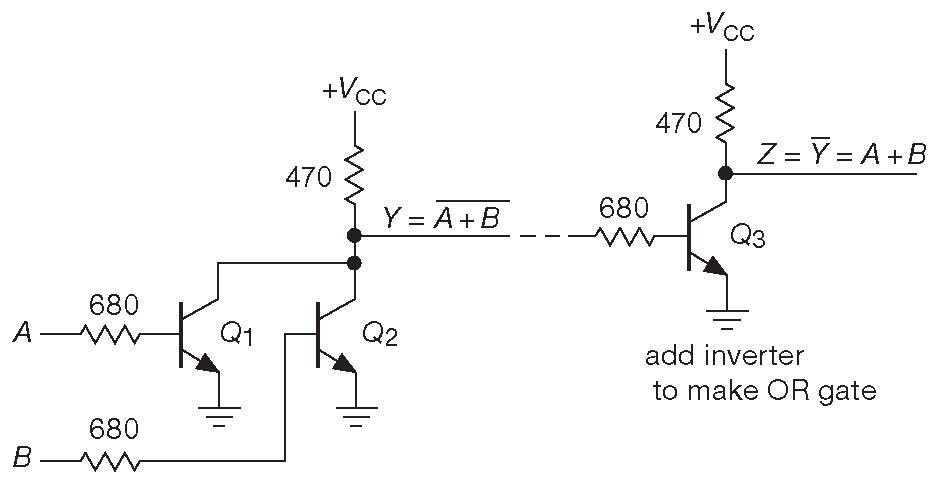
Рис. 10.13 Резисторно-транзисторная логика. Из элемента «ИЛИ-НЕ» и дополнительного инвертора можно собрать «ИЛИ»
Логические схемы на биполярных транзисторах практически полностью вытеснены МОП логикой. На рис. 10.14 показан тот же элемент «ИЛИ», но с ключами на n-канальных МОП транзисторах. МОП вариант не потребляет ток по входу, но его входная ёмкость потребует обеспечить ток перезарядки при смене состояния. Но и у такой схемы остаются недостатки. Скорость по-прежнему ограничена, а потребляемая мощность велика ( из-за резистивной подтяжки ). Обе проблемы красиво решает комплементарная МОП ( КМОП ) схема в симметричном включении ( см. обсуждение в §3.4.4.A ).
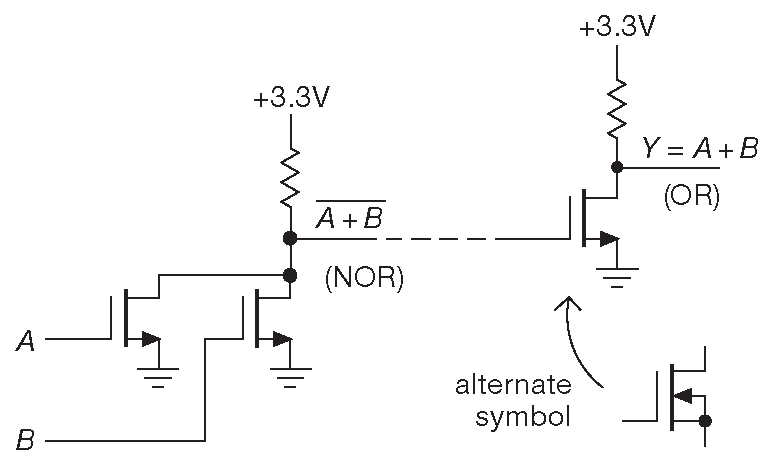
Рис. 10.14 Логический элемент «ИЛИ» на n-МОП транзисторах. Разработчики цифровых схем упростили символ МОП транзистора и не рисуют вывод подложки. Вдобавок они рисуют символ затвора по центру, а вместо стрелки указывают кружок - символ инверсии, что можно наблюдать на нижних транзисторах пар на рис. 3.6
==712
Показанная схема на дискретных транзисторах проста для понимания, но вряд ли найдёт применение в жизни 17 из-за имеющихся недостатков. Исключая экзотические случаи, собирать логические схемы из дискретных компонентов не требуется, т.к. очень широкая номенклатура отличных логических элементов доступна в виде готовых микросхем. Сегодня практически все логические ИМС выпускаются по КМОП технологии. Посмотрите на рис. 3.91 , чтобы вспомнить конструкцию КМОП элемента «И-НЕ».
10.1.6 Примеры схем на логических вентилях
Давайте изобразим схему, которая предлагалась в качестве примера в Части _1 [* §1.9.1.F ] и _2 [* §2.6.3 ] . Она подаёт сигнал об открытой двери, если водитель занял своё место. Схема станет очевидна, если сформулировать задачу правильно: «Выдать ВЫСОКИЙ уровень, если левая ИЛИ правая дверь открыта И водитель сидит». Получаем Q=(L+R)S . В виде схемы решение показано на рис. 10.15 . Выход элемента «ИЛИ» принимает ВЫСОКОЕ состояние, если какая-либо ( или обе ) дверь открыта. В этом случае и при сидящем водителе выходной сигнал Q станет ВЫСОКИМ. Дополнительный транзистор поможет запустить таким сигналом звуковой излучатель или активировать реле 18 .
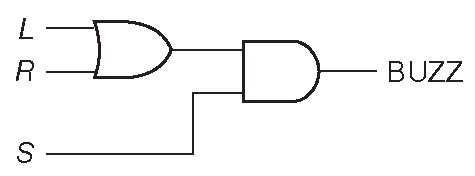
Рис. 10.15 Пример с автомобильными дверями. Схема для активных высоких сигналов
На практике кнопки, выдающие входные сигналы, скорее всего, замыкают соответствующую линию на землю, чтобы сократить, помимо прочего, число проводов. Это означает, что входной сигнал принимает НИЗКОЕ состояние, когда дверь открыта. Другими словами, имеем «активные низкие» сигналы. Давайте переделаем пример с учётом этого условия, а входные сигналы назовём /L, /R и /S .
Во-первых, надо знать, что какой-то сигнал от дверей имеет НИЗКОЕ состояние, т.е. нам требуется отлавливать состояние «оба входа ВЫСОКИЕ». Значит, требуется элемент «И». Подаём /L и /R на входы элемента «И». Его выход будет принимать НИЗКОЕ состояние, если какой-либо вход НИЗКИЙ. Назовём этот сигнал «/Какая-то-дверь». Теперь требуется, чтобы выполнялось условие /Какая-то-дверь= НИЗКИЙ и /S=НИЗКИЙ, т.е. требуется отлавливать состояние «оба сигнала НИЗКИЕ». Это элемент «ИЛИ». Схема показана на рис. 10.16 . Используется элемент «ИЛИ-НЕ», вместо вентиля без инверсии, чтобы на выходе схемы сигнал повторял логику схемы 10.15 : линия Q переходит в ВЫСОКОЕ состояние, когда заданное условие выполняется. Схема выглядит довольно странно: вместо «ИЛИ» стоит «И» и наоборот, если сравнивать со схемой 10.15 . Этот запутанный вопрос прояснит §10.1.7 , но сначала разберитесь с упражнением.
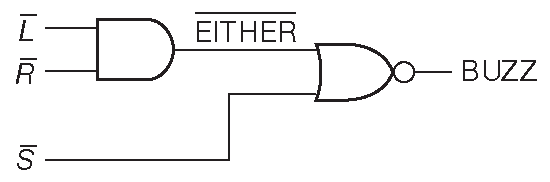
Рис. 10.16 Пример с автомобильными дверями. Активный низкий сигнал затрудняет прочтение схемы
==713
Упражнение 10.7
Разберитесь, что делают схемы на рис. 10.17
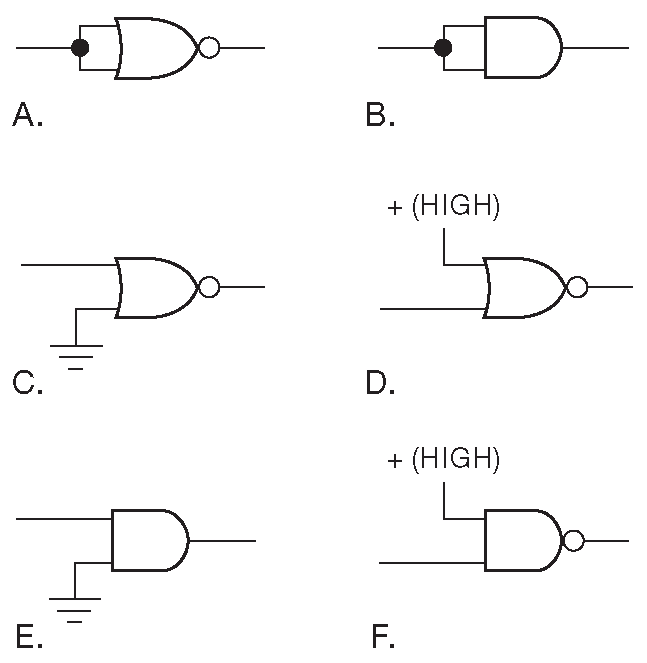
Рис. 10.17 Варианты включения логических элементов для упражнения 10.7
10.1.6.A Взаимные преобразования логических элементов
При создании цифровых схем учитывайте, что один вентиль можно переделать в другой. Например, требуется один элемент «И», но в наличии только половина 74LVC00 ( счетверённый вентиль «2И-НЕ» ). Его можно включить как на рис. 10.18 и получить искомое. Элемент на выходе работает в качестве простого инвертора, делая из «И-НЕ» просто «И». Следующие упражнения помогут закрепить материал.

Рис. 10.18 Превращение двух элементов «И-НЕ» в один «И»
Упражнение 10.8
Покажите, как, используя любое число 2-входовых элементов, сделать:
(a) инвертор из «ИЛИ-НЕ»;
(b) «ИЛИ» из «ИЛИ-НЕ» и
(c) «ИЛИ» из «И-НЕ».
Упражнение 10.9
Покажите, как сделать:
(a) 3-входовый «И» из 2-входовых «И»;
(b) 3-входовый «ИЛИ» из 2-выходвых «ИЛИ»;
(c) 3-входовый «ИЛИ-НЕ» из 2-выходовых «ИЛИ-НЕ» и
(d) 3-входовый «И» из 2-входовых «И-НЕ».
В общем случае для построения любой комбинационной функции достаточно одного типа инвертирующих вентилей ( например, «И-НЕ» [* имеет собственное имя «штрих Шеффера» и наряду со «стрелкой Пирса» - функцией «ИЛИ-НЕ» является базовым блоком для построения логических схем любой сложности, причём данный факт доказан математически ] ). Для неинвертирующих вентилей это утверждение неверно, потому что сделать из них элемент «НЕ» нельзя. Возможно, в этом кроется секрет большей популярности вентилей «И-НЕ» и «ИЛИ-НЕ».
10.1.7 Именование сигналов в соответствии с логикой высказываний
В вентиле «И» выход принимает ВЫСОКОЕ состояние, если оба входа имеют ВЫСОКИЙ уровень. Значит, если ВЫСОКИЙ означает «ИСТИННЫЙ», то выход переходит в ИСТИННОЕ состояние, только если оба входа ИСТИННЫЕ. Другими словами, в случае активной высокой логики вентиль «И» выполняет функцию «И». То же можно сказать и об «ИЛИ».
Что случится, если за ИСТИНУ будет принят НИЗКИЙ уровень? Элемент «И», на любом входе которого ИСТИННЫЙ ( НИЗКИЙ ) уровень выдаст ИСТИННЫЙ ( НИЗКИЙ ) на выход. Но это же функция «ИЛИ»?! Аналогично, вентиль «ИЛИ» выдаст ИСТИННЫЙ ( НИЗКИЙ ), только когда оба входа в ИСТИННОМ ( НИЗКОМ ) состоянии, т.е. работает как «И». Как это всё запутано!
Есть два пути решения проблемы. Первый - описанный ранее - выбрать вентиль, исходя из требуемого выходного уровня. Например, если требуется знать, что хотя бы один вход из трёх НИЗКИЙ, то надо брать 3-входовой элемент «И-НЕ». Кое-кто даже проектирует так схемы. В таком случае рисуется элемент «И-НЕ», хотя на самом деле выполняется операция «ИЛИ-НЕ» для активных низких входов. В этом случае схема будет выглядеть как на рис. 10.19 . Здесь /CLEAR, /MR и /RESET могут быть активными низкими сигналами, приходящими из разных точек схемы. Выход CLR - активный высокий, на котором появляется ВЫСОКИЙ уровень, когда какой-нибудь из входных сигналов переходит в НИЗКОЕ ( ИСТИННОЕ ) состояние.
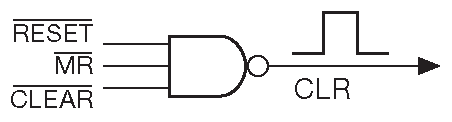
Рис. 10.19 Затеняющее суть изображение элемента, выполняющего функцию «ИЛИ» для активных низких сигналов
Другим путём решения проблемы активных низких сигналов является переход к «логике высказываний» . Если вентиль выполняет функцию «ИЛИ» для активных низких входов, то и в схеме надо рисовать «ИЛИ» ( рис. 10.20 ). 3-входовый элемент «ИЛИ» с инвертированными входами функционально идентичен 3-входовому «И-НЕ». Данная эквивалентность в свою очередь является одним из логических тождеств, вытекающих из теоремы ДеМоргана ( DeMorgan ). Они будут озвучены позднее, сейчас достаточно знать, что можно превращать «И» в «ИЛИ» и обратно, если инвертировать все входные и выходные сигналы ( см. табл. 10.3 ). Логика высказываний выглядит поначалу отталкивающе, потому что уродует симпатичные изображения логических элементов. Но на самом деле она лучше, потому что в таком виде логическая функция вентиля выявляется чётче. Она вам понравится через некоторое время, и переходить на что-то другое не захочется.
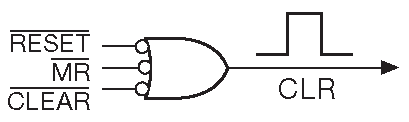
Рис. 10.20 Использование символов инверсии на активных низких входах
==714
Давайте переделаем пример с автомобильными дверями, но уже с учётом логики высказываний ( рис. 10.21 ). Левый вентиль с активным низким выходом выясняет в ИСТИННОМ ли, т.е. в НИЗКОМ ли, положении L или R . Правый вентиль выставляет ВЫСОКИЙ уровень, если L или R и одновременно S в ИСТИННОМ, т.е. в НИЗКОМ, состоянии. Из теоремы ДеМоргана следует, что левый вентиль «И», а правый - «ИЛИ-НЕ», в точности, как в предыдущем варианте. Два важных замечания.
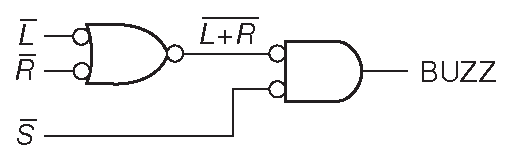
Рис. 10.21 Ещё раз про автомобильные двери. Логика высказываний исправляет сбивающую с толку схему 10.16
- Активный низкий ( или истинный низкий ) иногда называют «отрицательным истинным» , но это не означает, что логические уровни определяются отрицательным напряжением 19 . Это означает, что более низкий из двух уровней принят за значение «ИСТИНА»
- Схемное изображение вентиля предполагает активные высокие сигналы. Элемент «И-НЕ» может использоваться как «ИЛИ» для активных низких сигналов. Его можно рисовать как «И-НЕ» или, что лучше, в формате логики высказываний, т.е. как «НЕ-ИЛИ» со значками инверсии на входе ( с кружочками ). В последнем случае кружки воспринимаются как признак инверсии входных сигналов перед выполнением логической функции, следующей из символа вентиля. В нашем случае «ИЛИ», но уже для активных высоких сигналов 20 .
Возможно, правильнее было бы спросить, почему бы ни вести разработку, используя только активные высокие сигналы? Иногда выбор лимитирован самими используемыми компонентами ( например, чаще всего сброс в микроконтроллерах выполняется активным низким сигналом ), а случается, что, как в случае с дверями, удобнее использовать сигналы, замыкаемые на общую шину земли. И в любом случае надо уметь ориентироваться в цифровом мире, где есть и активные низкие, и активные высокие сигналы.
==714
12 Иногда называемые комбинаторными . <-
13 Альтернативой стандартной логике является «программируемая логика». В ней в одной недорогой микросхеме можно создавать свою схему из сотен или даже тысяч вентилей. Подробнее тема рассматривается, начиная с §10.5.4 и в Части 11 . <-
14 Бывают и исключения. Элемент ’1G386 заявляется в качестве «3-входового элемента ИСКЛЮЧАЮЩЕЕ-ИЛИ». Его можно назвать 3-входовым генератором чётности. <-
15 В исходных текстах употребляется неудобный символ «^». Возможно, потому что он есть на клавиатуре. Обычно его используют для всяких модификаторов букв в иностранных языках, но изобретательные отцы языков программирования постоянно находят для него иное применение. В листингах будет применяться более симпатичный символ «⋀» и плевать на вой поклонников рафинированного Си. <-
16 Такая схема использовалась в резисторно-транзисторной логике, которая была популярна в 1960-х годах, но сейчас полностью вышла из употребления. <-
17 В некоторых промышленных устройствах, где первостепенное значение придаётся надёжности и простоте, можно обнаружить схему, подобную 10.13 , собранную на обычных транзисторах. В таких местах можно использовать транзисторы с интегрированными базовыми резисторами (или делителями). Такие компоненты называют «цифровыми транзисторами» , «транзисторами с заданным смещением» или просто «транзистор с резистором в базе» . Это очень дешёвые компоненты ( до $0.02 в количествах ). Выпускаются ON semiconductor, Diodes Inc., Rohm и др. <-
18 Конкретно эта логическая схема как раз выпускается, имеет компактный корпус и называется 74LVC1G3208 – «3-входовой положительный ИЛИ-И элемент». Только не думайте, что такой сервис доступен для всех нужных вам вентилей. <-
19 Неправильное прочтение может привести к серьёзным неприятностям. Одному неопытному студенту была выдана микросхема синтезатора частоты. Он прочёл руководство, после чего подал –5V на входы программирования. Восстановление сгоревшей платы заняло довольно много времени. <-
20 Функции «И» и «ИЛИ» из формальной логики не следует путать с юридическими конструкциями. В увесистом томе под названием «Слова и фразы» более 40 страниц отведено описанию ситуаций, в которых «И» может трактоваться как «ИЛИ». Среди прочего отыскалось настоящее сокровище:
«ИЛИ может толковаться как И, а И толковаться как ИЛИ в соответствии с требованиями конкретной ситуации» .
Это не то, о чём говорит теорема ДеМоргана!
<-

