10.1 (I) Основные принципы работы логических схем
==703
10.1.1 Цифра против аналога
До настоящего момента преимущественно рассматривались схемы ( RC цепи, усилители, интеграторы ), входные и выходные сигналы которых менялись в некотором непрерывном диапазоне величин. Это естественное положение вещей, когда надо работать с непрерывными сигналами, например, со звуком или данными с датчиков.
Но существуют ситуации, когда сам входной сигнал имеет дискретную природу, скажем, выход детектора частиц или «битовые» данные с переключателя. В таком случае естественным и удобным становится использование цифровой электроники, которая имеет дело только с разными сочетаниями нулей и единиц. Более того, часто оказывается удобнее преобразовать непрерывный ( аналоговый ) сигнал в цифровое представление и обратно с помощью аналого-цифрового ( АЦП ) и цифро-аналогового ( ЦАП ) преобразователя. Это может потребоваться для обработки или хранения аналоговых величин в виде массива чисел. Типичным примером может служить микропроцессор, который наблюдает за экспериментом или производственным процессом и меняет режим функционирования оборудования на основе полученных данных, а их самих сохраняет для дальнейшего анализа.
Другим интересным примером возможностей цифровой техники является передача аналоговых сигналов без потери качества от наводок и шума. Аналоговый аудио- и видеосигнал легко набирает сторонние шумы при передаче по кабелю или радиоканалу в естественной форме. Шум, попавший в состав сигнала, удалить позднее не получится. Зато сигнал можно преобразовать в набор чисел, хранящих сведения об амплитуде в последовательные моменты времени. Теперь возможно передавать полученные числа как цифровой сигнал. С помощью ЦАПа на приёмной стороне можно восстановить исходную форму напряжения. Каких-либо ошибок от шума в канале связи не будет до тех пор, пока этот шум не мешает различать нули и единицы. Данная техника носит название PCM и особенно привлекательна, когда канал передачи содержит много промежуточных звеньев - репетиров, т.к. цифровые данные могут быть восстановлены в каждом промежуточном узле, что позволяет исключить шум канала. Данные и удивительные изображения, полученные космическим зондом PIONEER 10 в окрестностях Юпитера в 1973 г. сохранялись и передавались в формате PCM. Цифровой звук и телевизионное изображение присутствуют сегодня в каждом доме, как минимум в формате 12-сантиметровых звуковых лазерных дисков _1 . Данные на них сохраняются в виде значений со стерео каналов в виде двух 16-разрядных чисел каждые 23 микросекунды ( 1.4 Mbit/s ). Общий объём сохраняемых данных достигает 6 Gbit , что по сегодняшним стандартам является низкоскоростным носителем малой ёмкости. Соответствующие цифры для DVD и BD ( Blu-ray ) 10 и 48 Mbit/s (max), а информационная ёмкость - 38 и 200 Gbit на один слой.
Фактически цифровая аппаратура стала настолько мощной, что задачи ранее, решавшиеся аналоговыми методами, в настоящий момент проще реализовать цифровым способом. Например, аналоговый термометр может дополняться микропроцессором, который увеличит точность, компенсируя отклонения датчика от линейной характеристики. Аналогично устроены и бытовые напольные весы. Широкое распространение микроконтроллеров ценой менее доллара позволяет вставлять их практически в каждое устройство. Дома буквально набиты вещами, имеющими внутри процессор. Каждый музыкальный плеер, телеприёмник, сотовый телефон, посудомоечная машина, сушилка, факс, копировальный аппарат, микроволновая печь, кофе-машина... Список очень длинен и способен преподнести сюрпризы _2 . Чем пытаться назвать все области приложения цифровой электроники, лучше займёмся изучением её самой. Области использования будут появляться по ходу знакомства.
==704
10.1.2 Логические состояния
Под «цифровой электроникой» подразумеваются схемы, составленные из элементов только с двумя ( обычно ) состояниями, например, транзистор может находиться в насыщении или в отсечке. Как обычно, при описании используются напряжения, а не токи, причём уровни называются ВЫСОКИЙ и НИЗКИЙ. Два состояния могут быть представлены любым возможным «битом» - бинарным информационным элементом, в качестве которого могут выступать: одноразрядные двоичные числа, состояния электрического выключателя, наличие или отсутствие сигнала, нахождение некоторой аналоговой величины выше или ниже некоторого порогового уровня, факт регистрации какого-либо события или факт завершения некоторого действия и т.д.
10.1.2.A ВЫСОКИЙ и НИЗКИЙ уровни
ВЫСОКИЙ и НИЗКИЙ уровни напряжения представляют логические состояния ИСТИНА и ЛОЖЬ в булевой алгебре некоторым заранее оговоренным способом. Если в некоторой точке ВЫСОКИЙ уровень напряжения соответствует логическому значению ИСТИНА, то такой сигнал называется «активным высоким» ( или «высоким истинным» ) и наоборот. Поначалу это несколько сбивает с толку. На рис. 10.1 приведён пример. Состояние «ключ ЗАМКНУТ» является ИСТИННЫМ, т.е., когда на выходе НИЗКИЙ уровень, это «активный низкий» (или «низкий истинный»). Маркировать его следует в соответствии с надписью на рисунке. Горизонтальная линия над именем означает инверсию, т.е. на линии ВЫСОКИЙ уровень, когда ключ НЕ замкнут. Здесь просто надо запомнить, что наличие или отсутствие знака инверсии над именем говорит об уровне напряжения в линии, когда указанное состояние истинно _3 . В первый момент такая нотация кажется неестественной . Кажется, что будет проще отказаться от дополнительной инверсии и представлять сигналы в прямых обозначениях. Но из дальнейшего станет понятно, что «неестественный» путь бывает иногда удобнее.
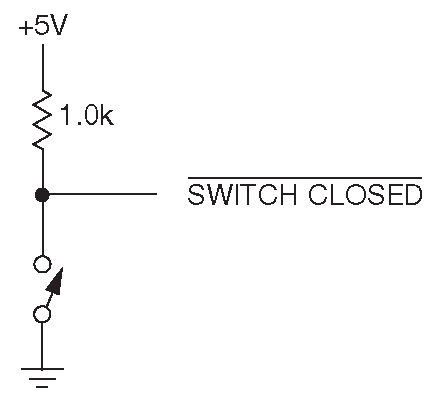
Рис. 10.1 Активный низкий логический уровень
Цифровые элементы «знают», что за сигнал к ним приходит, откуда он. Здесь всё в точности, как в аналоговых схемах, где известно, что делает выход конкретного ОУ. Но цифровые компоненты вносят в эту картину определённое разнообразие. Цифровые линии могут передавать данные, имеющие различную интерпретацию в различные моменты времени (мультиплексирование), или менять направление передачи. Для выполнения подобных действий требуется дополнительная информация - биты статуса или направления. Примеры этой очень удобной возможности можно будет увидеть позднее. На данный момент условимся, что каждое конкретное устройство собрано, чтобы выполнять некоторую определённую задачу, и известно, что это за задача, откуда приходят данные и куда они уходят.
Чтобы свести новизну к простому случаю, введём термины «0» и «1». Эти символы используются в булевой логике для обозначения понятия «ЛОЖЬ» и «ИСТИНА» соответственно и иногда работают в электронике именно так. К сожалению, есть и другое представление, когда «0» = НИЗКИЙ, а «1» = ВЫСОКИЙ. В данной книге сделана попытка снять неоднозначность использованием для обозначения логических состояний термина «ВЫСОКИЙ» ( или символа «H» ) и «НИЗКИЙ» ( «L» ). Символы «0» и «1» будут употребляться только в случае отсутствия неоднозначности.
10.1.2.B Диапазоны напряжений для НИЗКОГО и ВЫСОКОГО уровня
В цифровых схемах потенциалы, представляющие ВЫСОКИЙ и НИЗКИЙ уровень, должны попадать в некоторый диапазон, определяемый конкретным логическим семейством _4 . Например, скоростная КМОП логика ( семейство «HC» ), которая работает при питании +5V , будет интерпретировать все входные потенциалы между землёй и +1.5 V как НИЗКИЙ уровень, а все напряжения между +3.5 и +5V , как ВЫСОКИЙ _5 . На входы обычно подают сигналы с выходов других микросхем, и выходные уровни у всех у них должны быть 0V для НИЗКОГО и +5V для ВЫСОКОГО с точностью до десятых долей вольта. Выход определяется насыщающимся транзистором, подтягивающим вывод к нужной шине питания ( см. рис. 10.25 ). Такие границы упрощают учёт производственного разброса, температурных колебаний, просадок под нагрузкой и при изменении питающего напряжения, а также допускают некоторый уровень «шума» и случайного «мусора» на сигнальных линиях, который складывается с полезным сигналом на логическом входе. Шум и мусор могут быть следствием емкостных или магнитных наводок, интерференции с внешними цепями и т.д. Схема, принимающая сигнал расценивает его как ВЫСОКИЙ или НИЗКИЙ уровень с учётом наложения перечисленных факторов _6 . До тех пор, пока шум не может изменить логическое состояние, всё нормально, и шум исключается из сигнала на каждом этапе преобразования, а «чистый» уровень сигнала восстанавливается. При таком примитивном уровне рассмотрения цифровую электронику можно считать свободной от шума и идеальной.
==705
Термин помехоустойчивость используется для описания максимального уровня постороннего сигнала ( в худшем сочетании ), при котором ещё возможна безошибочная работа логического элемента. Например, популярное некогда семейство «транзисторно-транзисторной логики» ( TTL ) имело именно эту проблему. Её помехоустойчивость составляла всего 0.4 V . ТТЛ вход расценивал напряжение ниже +0.8 V в качестве НИЗКОГО уровня, а любое напряжение выше +2.0 V в качестве ВЫСОКОГО, в то время как выходные уровни для наихудшего случая составляли всего +0.4 и +2.4 V соответственно ( см. врезку с описаниями логических уровней ). На практике помехоустойчивость была выше 0.4 V , потому что типичные логические уровни составляли +0.2 и +3.4 V , а порог переключения располагался в районе +1.3 V . Но в хорошей разработке надо ориентироваться на наихудшее сочетание параметров. Полезно учитывать, что различные семейства имеют различную помехоустойчивость. У КМОП она выше, чем у ТТЛ, а у сверхскоростной эмиттерно-связанной логики ( ECL ) она ниже. [*] . Восприимчивость конкретной схемы к шуму зависит от многих факторов. Среди них амплитуда самого шума, которая зависит от жёсткости выходного каскада, индуктивности шин питания, наличия протяжённых линий связи, скорости переключения из одного логического состояния в другое. При быстром переключении возникают импульсные токи в шинах питания и, соответственно, выбросы напряжения на них, вызванные индуктивностью проводников и ёмкостным характером нагрузки. Эти проблемы подробно обсуждаются в Части 12 ( «Сопряжение логических сигналов» ).
[*]
[* Здесь стоит заметить, что хотя напряжения и в самом деле отличаются не сильно, но НИЗКИЙ уровень ТТЛ определяется низкоомным источником, который обязан принять ток со входа. То же можно сказать об ЭСЛ. Короче, всё у ТТЛ хорошо с помехоустойчивостью ].
10.1.3 Кодирование чисел
Большая часть числовых данных, использовавшаяся до настоящего момента, не требовала дополнительных пояснений. Но вопрос с представлением чисел с помощью логических уровней достаточно сложный и интересный предмет. Скажем иначе: ранее отдельные биты использовались в качестве индикатора , а теперь требуются группы битов для представления чисел .
В десятичной системе ( с основанием 10 ) числа - просто цепочка цифр, каждая из которых умножается на соответствующую степень числа 10 , а потом эти произведения складываются вместе. \[ 137.06 = 1×10\space^2 + 3×10\space^1 + 7×10\space^0 + 0×10^{-1} + 6×10^{-2}. \]
[* Авторы путают понятие «десятичная» и «позиционная» система счисления и объясняют последнюю, называя её «десятичной». Но основание системы полностью независимо от метода представления числа, что они же с успехом и продемонстрируют на примере двоичной системы (с основанием 2 ) ].
Здесь требуются десять символов от «0» до «9» и множители в виде степеней 10 , причём множитель выбирается в зависимости от позиции цифры относительно десятичной точки. Если требуются числа, использующие два символа ( «0» и «1» ), то нужна двоичная система счисления или система с основанием 2 . Каждый 0 и 1 такого числа умножается на соответствующую степень числа 2 . \[ 1101\space_2 = 1×2\space^3 + 1×2\space^2 + 0×2\space^1 + 1×2\space^0 = 13\space_{10}. \]
Индивидуальные нули и единицы представляют один разряд ( бит ) двоичного числа. Нижний индекс при числе сообщает основание системы счисления и всегда выражается десятичным числом, чтобы избежать многозначности, ведь цифры-то все одинаковые.
Метод преобразования двоичных чисел в десятичные показан выше. Для преобразования в обратном направлении число последовательно делится на 2 [* или иное требуемое основание степени ] с получением остатков от деления [* они всегда меньше основания системы счисления ] . Таким образом, для преобразования \(13\space_{10}\) в двоичное представление надо:
13/2 = 6 остаток 1 , 6/2 = 3 остаток 0 , 3/2 = 1 остаток 1 , 1/2 = 0 остаток 1 .
Получили \(13\space_{10}=1101\space_2\). Примечательно, что ответ получен в обратном порядке - от младшего значащего разряда ( LSB ) к старшему ( MSB ).
10.1.3.A Шестнадцатеричное представление
Двоичное представление является естественным выбором для систем с двумя состояниями ( но это не единственный вариант, что будет показано ниже ). Двоичные числа получаются довольно длинными [* а главное унылыми - одни лишь нули и единицы - никакого разнообразия ] , поэтому их часто записывают в шестнадцатеричной форме, т.е. с основанием 16 . Каждой позиции итогового числа соответствует степень числа 16 , каждый шестнадцатеричный символ принимает значение от \(0\) до \(15\space_{10}\) (привычные цифры дополняются символами \(A_{16}\)...\(F_{16}\) для «цифр» \(10\space_{10}\) ...\(15\space_{10}\) ). Чтобы перевести двоичное число в шестнадцатеричной форме, надо разбить двоичные разряды, начиная с LSB, в группы по 4 бита и записать шестнадцатеричный эквивалент для каждой группы: \[ 707\space_{10} = 1011000011\space_2 \space (= 10\space 1100\space 0011\space_2) = 2C3\space_{16}\space. \]
==706
Шестнадцатеричное представление _7 хорошо подходит для популярного кратного «байту» ( 8 битам ) деления разрядной сетки современных компьютеров. Чаще всего можно встретить 8-, 16-, 32- и 64-разрядные машинные слова ( 1, 2, 4 и 8 байт ). В шестнадцатеричном представлении на каждый байт нужно две цифры. Скажем, для микроконтроллера, имеющего 65536 байт памяти ( «64K» ), требуется 2-байтный адрес, т.к. 216=65536 . Младший адрес при этом равен 0x0000 , а старший - 0xFFFF , вторая половина адресного пространства начинается с 0x8000 , а последняя четверть - с 0xC000 .
Байт данных в памяти компьютера может представлять число или его часть, но, кроме того, он может означать нечисловые понятия. Примером может служить ASCII код для алфавитно-цифрового набора символов ( см. §14.7.8 ). Строчная латинская «a» в нём представляется числом 0x61 ( 0110 0001 ), «b» - 0x62 и т.д., поэтому слово «four» можно сохранить в последовательных байтах памяти со значениями «0x66, 0x6F, 0x75, 0x72».
10.1.3.B Двоично-десятичные числа
Ещё одним способом представления чисел является двоичная кодировка каждой отдельной десятичной цифры. Метод носит название «двоично-десятичное кодирование» ( BCD ) и требует 4 двоичных разряда для одного десятичного. Например, \[ 137\space_{10} = 0001\space0011\space0111\space_{BCD}\space. \]
ЛОГИЧЕСКИЕ УРОВНИ
Рис. 10.2 показывает диапазоны напряжений, соответствующих двум логическим состояниям ( НИЗКОЕ и ВЫСОКОЕ ) для популярных семейств цифровой логики. Для каждого семейства необходимо указать допустимые величины входных и выходных напряжений для НИЗКОГО и ВЫСОКОГО состояния. Закрашенные области над шкалой напряжений указывает специфицированный диапазон вЫходных напряжений, которые выдаст микросхема в соответствующем состоянии, а пара стрелок показывает типичные уровни, встречающиеся на практике. Закрашенные области под шкалой указывают диапазон, в котором сигнал гарантированно будет воспринят как НИЗКИЙ или ВЫСОКИЙ, а стрелка отмечает типичное значение порога переключения , т.е. границы между НИЗКИМ и ВЫСОКИМ уровнем. Во всех случаях ВЫСОКИЙ уровень положительнее НИЗКОГО. Дополнительные сведения по упомянутым логическим семействам можно найти в табл. 10.1 и на рис. 10.26 , а детальное описание приводится в Части 12 .
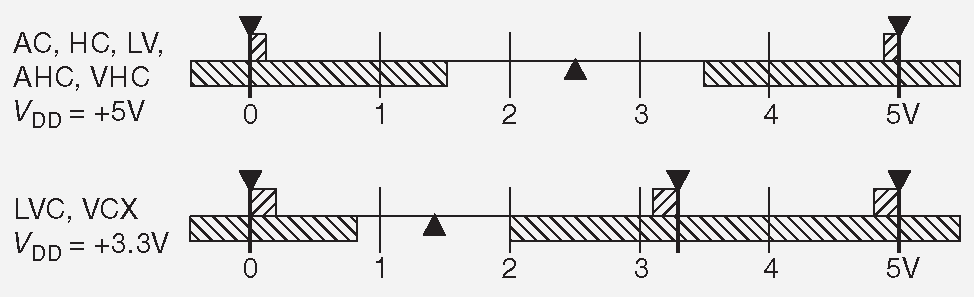
Рис. 10.2 Напряжения логических уровней некоторых популярных семейств
Смысл терминов «минимальный», «типичный» и «максимальный» из электронных спецификаций требует некоторых пояснений. Дело в том, что производитель компонента гарантирует, что его параметры попадут в «вилку» минимум-максимум и будут группироваться возле «типичного» значения. Это значит, что типичные значения являются лишь приблизительными и всего лишь влияют на разработку устройства. Схема должна работать правильно в широком диапазоне специфицируемых значений от минимума до максимума, которые определяются технологическими возможностями производства. Хорошо спроектированная схема должна функционировать при самом плохом сочетании максимальных и минимальных значений. Такой подход известен под названием консервативная разработка ( для наихудших или гарантированных производителем параметров ). Именно так надо проектировать приборы, рассчитанные на сборку из обычных компонентов, не проходящих входной отбор.
Table 10.1 Selected Logic Families Family CO 0 =3 O 03 4— =3 C 03 Supply voltage (Vcc) Vin max fpd @ (ns, typ) Vcc (V) Available packages min (V) max (V) CL Q 1- if) o CM u 74HC00 9 2 6 Vcc 9 5 • • • 74AC00 5 3 6 Vcc 6 5 • • - 74AHC00 2 2 5.5 Vcc 3.7 5 • • • 74LV00 2 1.2a 5.5 5.5 3.6 5 • • • 74LVC00 4 1.7 3.6 5.5 3.5 _Q CO CO - • • 74ALVC00 3 1.7 3.6 3.6 2 3.3c - • - 74AUC00 1 0.8 2.7 3.6 0.9 1.8 - • • Notes: (a) NXP only (TI specs to 2V only). (b) 6ns @ 1.8 V. (c) 2.7ns @ 1.8 V.
==707
Отметим, что BCD кодировка - не то же самое, что двоичная, которая для предложенного примера будет \(137\space_{10} = 10001001\space_2\) . В BCD каждый разряда числа, начиная с LSB, соответствует следующему ряду значений: 1, 2, 4, 8, 10, 20, 40, 80, 100... Видно, что BCD относится к информационной ёмкости довольно расточительно, потому что 4 разряда могут представлять числа от 0 до 15 , а в BCD верхней границей является 9 . Тем не менее, BCD - идеальный формат, если требуется индицировать десятичные цифры, т.к. число в таком формате достаточно подать на дешифратор индикатора группами по 4 бита [* оно не требует перевода из одного основания в другое ] . По этой причине BCD часто используется при вводе-выводе числовой информации [*] . К сожалению, перевод из двоичного представления в BCD и обратно достаточно сложен. Поэтому, с учётом более удобной арифметики для чисто двоичных чисел, современные компьютеры конвертируют BCD в двоичное представление сразу после получения, а обратное преобразование ведут непосредственно перед выводом данных. Прикиньте, сколько бы выгоды получил homo sapiens , оперируя числами в 8- ( или 16- ) ричной системе _8 .
[*]
[* Личный опыт. Требовалось организовать легко читаемый вывод нескольких многоразрядных десятичных чисел, которые надо было заносить в лабораторный журнал в «естественной» ( десятичной ) форме. BCD кодировка оказалась чрезвычайно удобной для отображения сама по себе без каких-либо дополнительных преобразований.
Индикатор ( 4 линейки по 12 разрядов в BCD кодировке с возможностью расширения разрядной сетки ) прожил более 20 лет и пережил несколько полных переделок лабораторной электроники. Каждая десятичная цифра ( естественное горизонтальное расположение, старшие разряды слева ) отображалась столбиком из четырёх лампочек ( сверху 8 , снизу 1 ), отвечающих за двоичные разряды. Получился очень простой индикатор с естественным расположением и десятичных, и двоичных разрядов, простой ( из-за отсутствия декодера и специального дисплея ), дешёвый, очень надёжный и чётко читаемый. Так как реализовано это всё было на обычных двоично-десятичных счётчиках пульсаций ( см. §10.5.2.B ), наращивать разрядную сетку можно было без труда. Использовалось это чудо в некоем физическом оборудовании в качестве многоканального регистратора событий. Дополнительным плюсом был примитивизм накопительного счёта-отображения ( без каких-либо стробов - только общий сигнал очистки ). В результате заполнение счётчика выглядело как цепочка светящихся столбиков, растущих в область старших разрядов, скорость мигания которых позволяла оценить интенсивность наблюдаемого процесса ].
Упражнение 10.1
Преобразуйте в десятичную систему: (a) \(1110101.0110\space_2\), (b) \(11.01010101...\space_2\) (c) \(2A\space_{16}\) .
Преобразуйте в двоичное представление (a) \(1023\space_{10}\), (b) \(1023\space_{16}\) .
Преобразуйте в шестнадцатеричную систему: (a) \(1023\space_{10}\), (b) \(101110101101\space_2\), (c) \(61453\space_{10}\) .
10.1.3.C Числа со знаком
- Прямой код со знаком
- Раньше или позже в вычислительном устройстве потребуется как-то выразить через двоичное представление отрицательные числа. В самом простом случае достаточно будет выделить один бит (например, старший) под знак, а в оставшихся битах записать абсолютную величину числа. Такая форма называется «прямой код со знаком» и соответствует естественной форме записи чисел со знаком ( см. табл. 10.2 [* и §13.1.2 ] ). Данный формат применяется при выводе цифр на индикатор и в некоторых АЦП. В общем случае это не лучший выбор для представления чисел со знаком ( если исключить числа с плавающей запятой ), особенно если они будут участвовать в расчётах. Причин несколько. Сложная математика, и разные процедуры сложения и вычитания ( т.е. сложение не будет работать с отрицательными числами ). Кроме того, имеется два нуля ( +0 и –0 ), и надо учитывать данный факт, выбирая что-то одно.
- Двоичный код со смещением
- Вторым методом представления отрицательных чисел служит «код со смещением» . В нём из числа вычитается половина максимального представимого значения ( табл. 10.2 ). Преимуществом такого формата является сквозное изменение кода от самого отрицательного значения к самому положительному в виде простой арифметической прогрессии, как она реализована в обычном двоичном счётчике. MSB по-прежнему хранит информацию о знаке, а нулевое значение встречается только один раз. Код со смещением часто используется в аналого-цифровых преобразователях, но всё ещё неудобен для расчётов.
- Код с дополнением до двух
- Чаще всего используемый в двоичных арифметических устройствах код называется «дополнением до двух» . В нём положительное число представляется «как есть» - двоичным числом без знака. Изменения касаются представления отрицательных значений. Они выражаются двоичным числом, которое надо прибавить к положительному числу такой же величины [* по модулю ] , чтобы получить нуль. Для этого надо инвертировать все разряды положительного числа ( т.е. нули в каждом разряде заменяются единицами и наоборот, операция называется «дополнение до единицы» ) и добавить к результату единицу ( получается «дополнение до двух» ) _9 . По табл. 10.2 легко заметить, что «дополнение до двух» совпадает с «кодом со смещением» с точностью до MSB: он инвертирован. Как и в других кодовых схемах MSB хранит информацию о знаке. Здесь есть только один нуль, имеющий, к тому же, привычное представление - нули во всех разрядах ( как после операции «сброса» счётчика или регистра ). «Дополнение до двух» позволяет арифметическому устройству работать с положительными и отрицательными числами одинаковым образом, поэтому данная схема повсеместно используется при целочисленных расчётах 10 .
Table 10.2 4-Bit Signed Integers in Three Systems of Representation
Integer Sign-magnitude Offset binary 2's comp +7 0 111 1 111 0 111 +6 0 110 1 110 0 110 +5 0 101 1 101 0 101 +4 0 100 1 100 0 100 +3 0 011 1 011 0 011 +2 0 010 1 010 0 010 +1 0 001 1 001 0 001 0 0 000 1 000 0 000 -1 1 001 0 111 1 111 -2 1 010 0 110 1 110 -3 1 011 0 101 1 101 -4 1 100 0 100 1 100 -5 1 101 0 011 1 011 -6 1 110 0 010 1 010 -7 1 111 0 001 1 001 -8 - 0 000 1 000 (-0) 1 000 - -
==708
10.1.3.D Арифметика в формате с дополнением до двух
Арифметика в формате «с дополнением до двух» проста. Чтобы сложить числа, их просто надо поразрядно ( с переносом ) сложить:
5+(–2)=3 : 0101 | +5 +1110 | –2 =0011 | +3
Чтобы вычесть B из A , надо взять дополнение до двух от B и сложить его с A :
2–5=–3 : 0010 | +2 +1011 | –5 =1101 | –3
Отметим, что в последнем примере +5 =0101 , поэтому его поразрядная инверсия ( «дополнение до единицы» ) равно 1010 , а дополнение до двух (+1) 1011 . Умножение с числами в формате «с дополнением до двух» также работает правильно.
Упражнение 10.2
Проведите умножение +2 на –3 , где –3 представлено в виде «дополнения до двух».
Подсказка : ответ «–6».
Упражнение 10.3
Покажите, что дополнение до двух для –5 равно +5 .
При сложении или вычитании чисел можно получить переполнение [* число большее максимального ] или антипереполнение [* число меньшее минимального ] . Беззнаковое целое длиной n бит может принимать значения от 0 до 2(n-1) , а n-разрядное знаковое целое в коде «с дополнением до двух» может хранить числа от –2(n-1) до +2(n-1)–1 . Для 8 разрядов это диапазон 0...255 и –128...+127 . Чтобы понять вызывает ли операция над беззнаковыми числами переполнение (т.е. корректно ли действие), надо посмотреть, будет ли перенос из MSB. При знаковых операциях в формате «с дополнением до двух» ситуация несколько сложнее. Если знаковый разряд MSB изменяется переносами , т.е., если перенос в MSB не уравновешивается переносом из него, то результат ошибочен.
Упражнение 10.4
Проверьте это необычное условие, выполнив сложение в коде «с дополнением до двух» для каждой из предложенных знаковых пар, используя 4-разрядные слова: 7+(–6); 7+7; 7+4; –7+(–8). Повторите те же действия с 5-разрядными словами. Во втором случае все ответы умещаются в разрядную сетку.
10.1.3.E Код Грея
Этот код среди прочего используется в механических линейных и угловых энкодерах и некоторых АЦП и носит название «кода Грея» 11 . Основное его свойство заключено в изменении только одного разряда при переходе из любого состояния к одному из двух соседних. Данное свойство гарантирует от появления случайного некорректного состояния битов при таком переходе. В противном случае в выходном потоке возможно появление промежуточных ошибочных состояний, т.к. невозможно гарантировать одновременность переключения всех разрядов одновременно на границе между двумя числами. При использовании простого двоичного кода возможно кратковременное появление на выходе состояния «7» при переключении из состояния «3» в состояние «4». Для создания кода Грея есть простое правило. Надо начать с кода «все нули». Для получения следующего состояния надо переключить самый младший бит, который позволит получить ещё не использовавшееся сочетание разрядов.
State Binary Gray 0 000 000 1 001 001 2 010 011 3 011 010 4 100 110 5 101 111 6 110 101 7 111 100
На рис. 10.3 показан угловой энкодер с кодом Грея, который позволяет исключить появление ошибочных сочетаний при переходах. Код Грея можно составить для любого числа разрядов. Он находит применение и в «параллельных кодировщиках» ( их ещё зовут флэш-конверторы ) - скоростных АЦП, которые появятся в Части 13 . Разговор о взаимном преобразовании двоичного кода и кода Грея будет чуть дальше при разборе схемной реализации на рис. 10.10 .
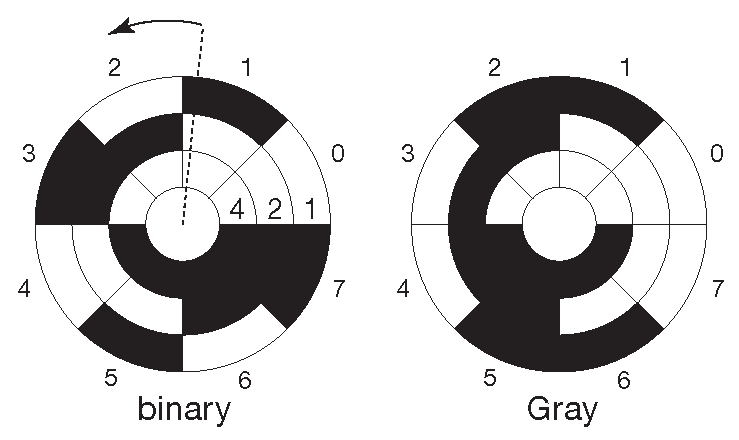
Рис. 10.3 Два варианта 3-разрядных угловых энкодеров. Белые и чёрные сектора соответствуют нулевым и единичным состояниям разрядов 1 , 2 и 4 в выходном коде. В двоичном коде возможно появление ошибочных состояний, подобных переходу «1» → «2» (показан пунктиром), когда возможно одновременное изменение состояния нескольких битов. В коде Грея данная проблема отсутствует
==708
1 И их видео вариантами - DVD и BD (Blu-ray) дисками <-
2 Историю победы цифровых методов над аналоговыми можно было бы обозначить следующими этапами. 1970-е годы. Фотоизображения других планет, но домашняя жизнь продолжает оставаться в основном аналоговой. 1980-е годы. Цифровой звук ( CD ) и появление в домах компьютеров. 1990-е. Цифровое видео ( DVD ), сотовые телефоны, MP3. 2000-е. HDTV, беспроводная цифровая связь, цифровая фото- и видеосъёмка, скоростные интернет-каналы, Google. 2010-е. ( Ну, да. «Трудно предсказывать, особенно будущее» ). Повсеместное проникновение цифровых методов и сращивание информации и среды её доставки. <-
3 В дальнейшем будут встречаться термины «положительная истинность» и «отрицательная истинность» . Они используются для состояний ВЫСОКИЙ=ИСТИНА и НИЗКИЙ=ИСТИНА соответственно. Это вполне обычные термины, но смущают поначалу, особенно если отрицательных напряжений в системе нет. <-
4 Семейство - обычная форма реализации цифровых ИМС. Оно характеризуется рабочим напряжением, напряжениями логических уровней и быстродействием. По историческим причинам наименование большей части логических семейств начинается с префикса «74», за которым следует несколько букв, указывающих семейство, и несколько цифр, сообщающих логическую функцию. Логические функции были одинаковыми во всех семействах [* с префиксом «74» или «54» ] . Например, «74LVC08» - вентиль «И» с двумя входами ( четыре штуки в одном корпусе ), относится к низковольтному КМОП семейству ( «LVC» ), а «74» обозначает логическую микросхему, работающую в стандартном температурном диапазоне. <-
5 На врезке «Логические уровни» [* на стр. 706 ] есть дополнительные примеры. <-
6 Иногда цифровые сигналы передают по дифференциальным парам [* где логический уровень определяется разницей потенциалов двух линий, а не абсолютной величиной напряжения, как в несимметричном варианте ( SE ) ] . Такой способ очень популярен при дальней передаче высокочастотных сигналов и для линий, выходящих за пределы устройства, например, в быстрых последовательных шинах USB, Firewire или SATA. Так же раздаются высокочастотные тактовые сигналы. Популярным дифференциальным форматом является LVDS , в котором дифференциальные сигналы амплитудой ∼0.3 V группируются вокруг среднего уровня +1.25 V . <-
7 Шестнадцатеричные числа чаще всего представляются в следующих формах ( для \(2C3_{16}\) ): \( 2C3H \) и \( 0x2C3 \) без учёта регистра символов. [* Первый - ассемблерный, второй ( наиболее распространённый ) – «сишный». Во всех случаях число должно начинаться с легальной десятичной цифры, т.е. в «сишной» нотации выполняется всегда, а в ассемблерной требует лидирующего нуля перед числами, начинающимися с цифр \(A_{16}\)...\(F_{16}\) ] . <-
8 В первом варианте проще счёт, но длиннее запись. <-
9 Или иначе, можно рассматривать их в качестве простых беззнаковых величин, а MSB считать признаком отрицательного числа. <-
10 Но «числа с плавающей запятой» представляются в виде «знак величина», а именно знак-экспонента-мантисса . <-
11 Фрэнк Грей ( Frank Gray ) из Bell Telephone Laboratories получил патент на импульсную кодовую модуляцию ( PCM ) в 1953г. В нём был обнародован «новый код» для аналого-цифровых преобразований, который Грей назвал «зеркальный двоичный код» . Сейчас этот код зовут «кодом Грея» . Но на самом деле код был открыт ранее самим Эмилем Бодо ( из его фамилии вышел «бод» ), который применил его в телеграфии в 1878г. <-

