3.3 Подробный разбор параметров полевых транзисторов

==165

В §3.1.4 были схематически обозначены рабочие зоны полевых транзисторов. Для напряжений на стоке от вольта и выше ( вне «линейной» резистивной области ) расположен обычный рабочий регион, в котором ток насыщения ⁵⁵ стока $I_D$ пропорционален $(V_{GS}-V_{th})^2$ , и слаботочная подпороговая область, в которой $I_D$ имеет экспоненциальную зависимость от $V_{GS}$ .

[* Т.е. область напряжений сток-исток –0.5 V<$V_{DS}$<+0.5 V - «резистивная ( линейная ) область», где напряжение на затворе, точнее $(V_{GS}-V_{th})$ , управляет «номиналом резистора сток-исток». Данная область есть у любого полевого транзистора с любым типом затвора ( и с p-n переходом, и изолированного ) обеих полярностей. А вне линейной лежат «квадратичная» ( открытый транзистор, нормальный ток ) и «подпороговая» ( почти закрытый транзистор и ток, на пару-тройку порядков меньше обычного ). Эти две различаются напряжениями на затворе, см рис. 3.16 , на котором хорошо виден переход между ними. И вновь, «активные» области есть у всех транзисторов, но знаки на электродах теперь зависят от типа ( обогащённый, обеднённый, т.е. со встроенным или с индуцированным каналом ) и полярности ( n- или p-канальный ).

«Некоторые пояснения никогда не помешают, хотя делают их редко» Х&Х ].

Это несколько упрощённая картина. ПТ - приборы, которые выбирают для точных малошумящих схем с высоким входным импедансом. Будет полезно посмотреть внимательнее на их особенности, в идеале с данными измерений конкретных образцов.

Пришлось предпринять всесторонний ( и утомительный! ) обзор большинства доступных ПТ, набрать тестовую группу для каждого типа, часто и для нескольких производителей. Табл. 3.7 ( стр. 217 ) включает их большую часть и сообщает некоторые измеренные параметры ( $I_{DSS}$ , $g_{os}$ , $g_m$ и $V_{GS}$ на интересных для работы токах стока ) и цифры из справочных данных ⁵⁶. См. также табл. 8.2 ( стр. 516 ), в которой перечислены малошумящие транзисторы.

Некоторые дополнительные темы разбираются в Части X3 , а здесь рассматриваются самые базовые вопросы: рабочие области полевых транзисторов, включая подпороговую , которая часто остаётся в тени, их крутизну и ёмкость.

3.3.1 Зависимость тока стока от напряжения на затворе

Одной из проблем, постоянно довлеющих над разработчиком, является разброс цифр . Он хорошо виден на рис. 3.51 и 3.52 , где приводятся данные для шести экземпляров n-канальных 2N5457 ( по три штуки от двух производителей ⁵⁷ ) и трёх экземпляров близких по параметрам 2N5458 ( оба типа входят в одно семейство 2N5457-59 ). В каждом случае приведены данные для верхней границы, нижней границы и медианы измеренных значений $I_{DSS}$ для 10 образцов. При измерениях потенциал затвора заходил в область положительных напряжений (рядом с границей начала проводимости p-n перехода затвора) за обычную границу нулевого смещения относительно истока. Ничего ужасного не произошло, но при нормальных обстоятельствах такой практики следует избегать.

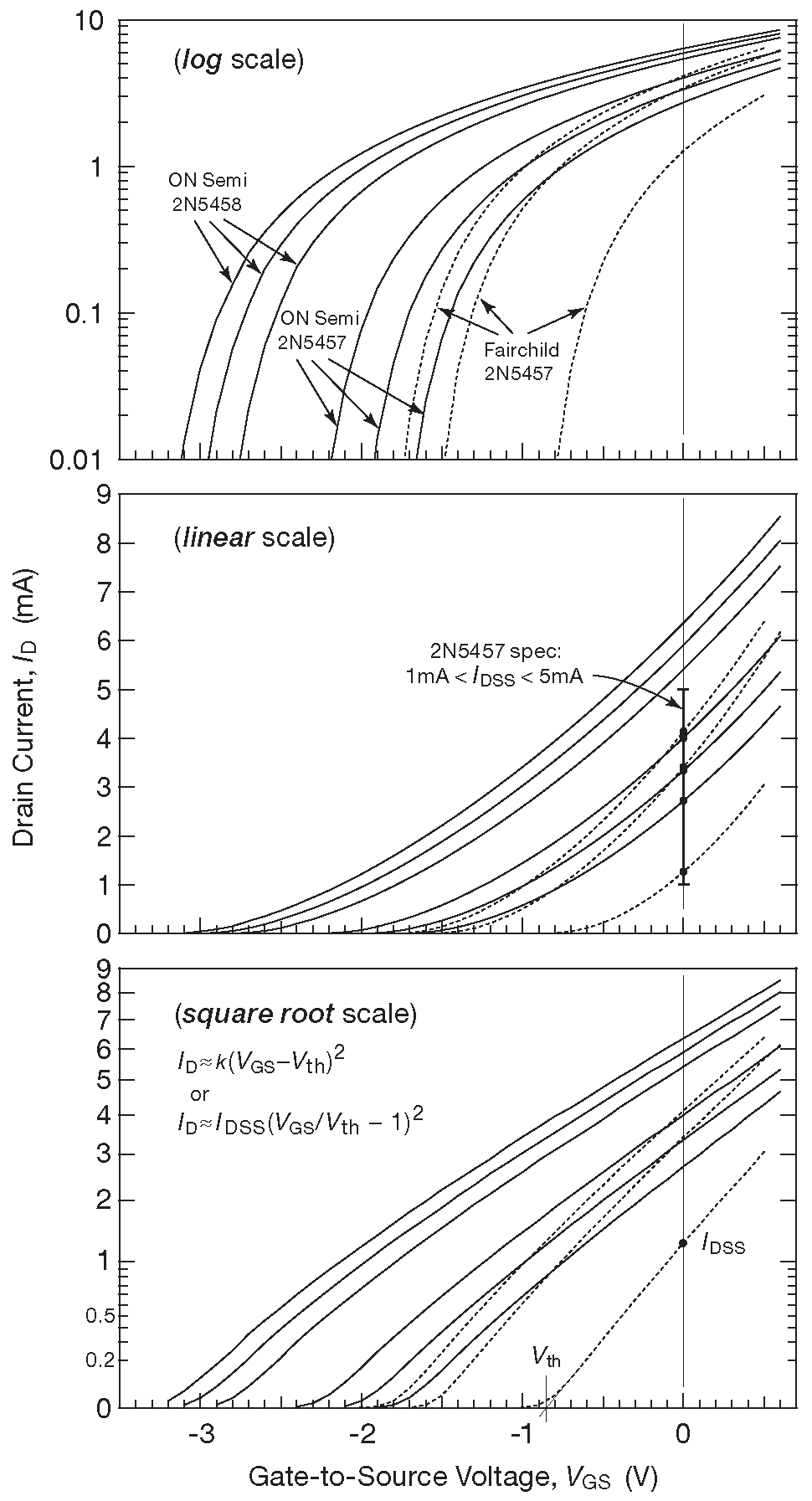
Рис. 3.51 Зависимость тока стока от напряжения на затворе для девяти образцов из набора n-канальных 2N5457/58/59 при $V_{DS}$=5V . Одни и те же данные представлены в трёх формах: линейной, логарифмической и в виде квадратного корня. Компоненты ON Semi и Fairchild соответствуют спецификации по $I_{DSS}$ ( средний рисунок ), хотя имеют заметно отличающиеся графики. Обратите внимание, что графики уходят за $I_{DSS}$ до $V_{GS}$=+0.6V

Рассмотрим подробно данные этих девяти образцов, чтобы разобраться в различных особенностях их параметров, влияющих на разработку.

3.3.1.A Квадратичный регион

Линейный график - вот что обычно можно обнаружить в справочных данных и учебниках. В логарифмическом масштабе хорошо видна квадратичная зависимость тока стока после достижения им существенной доли от величины $I_{DSS}$ ( тока стока при нулевом смещении ). Именно в этом режиме обычно работает ПТ с p-n переходом, см. [3.4] . На графике видна разница в $I_{DSS}$ нескольких экземпляров ( на вертикальной границе нулевого смещения отмечен диапазон из спецификации, в который попали 6 штук 2N5457 ). Образцы от Fairchild имеют чуть более резкий подъём. Подъём - это крутизна $g_m=dI_D/dV_{GS}$ , которая линейно растёт вместе с $V_{GS}$ , см. [3.5] . В этом режиме ток стока равен квадрату разницы $(V_{GS}-V_{th})$ .

==166

Нахождение $V_{th}$ : график квадратного корня

Далее смотрим на график квадратного корня тока стока, который позволяет выявить доселе скрытые обстоятельства. Экстраполяция до «нулевого» тока позволяет выяснить $V_{th}$ [* см. нижнее изображение на рис. 3.51 ] . При этом напряжении ток на самом деле не нулевой , он просто очень близок к верхней границе подпороговой области.

3.3.1.B Подпороговая область

Наконец, логарифмический график отлично показывает область малых токов. Изогнутые линии, плавно переходящие [* по мере ухода $V_{GS}$ в отрицательную область ] в прямые ( т.е. экспоненты ) отражают поведение при самых низких токах. Это и есть подпороговая область, которая показана ещё на 6 порядков глубже на рис. 3.52 .

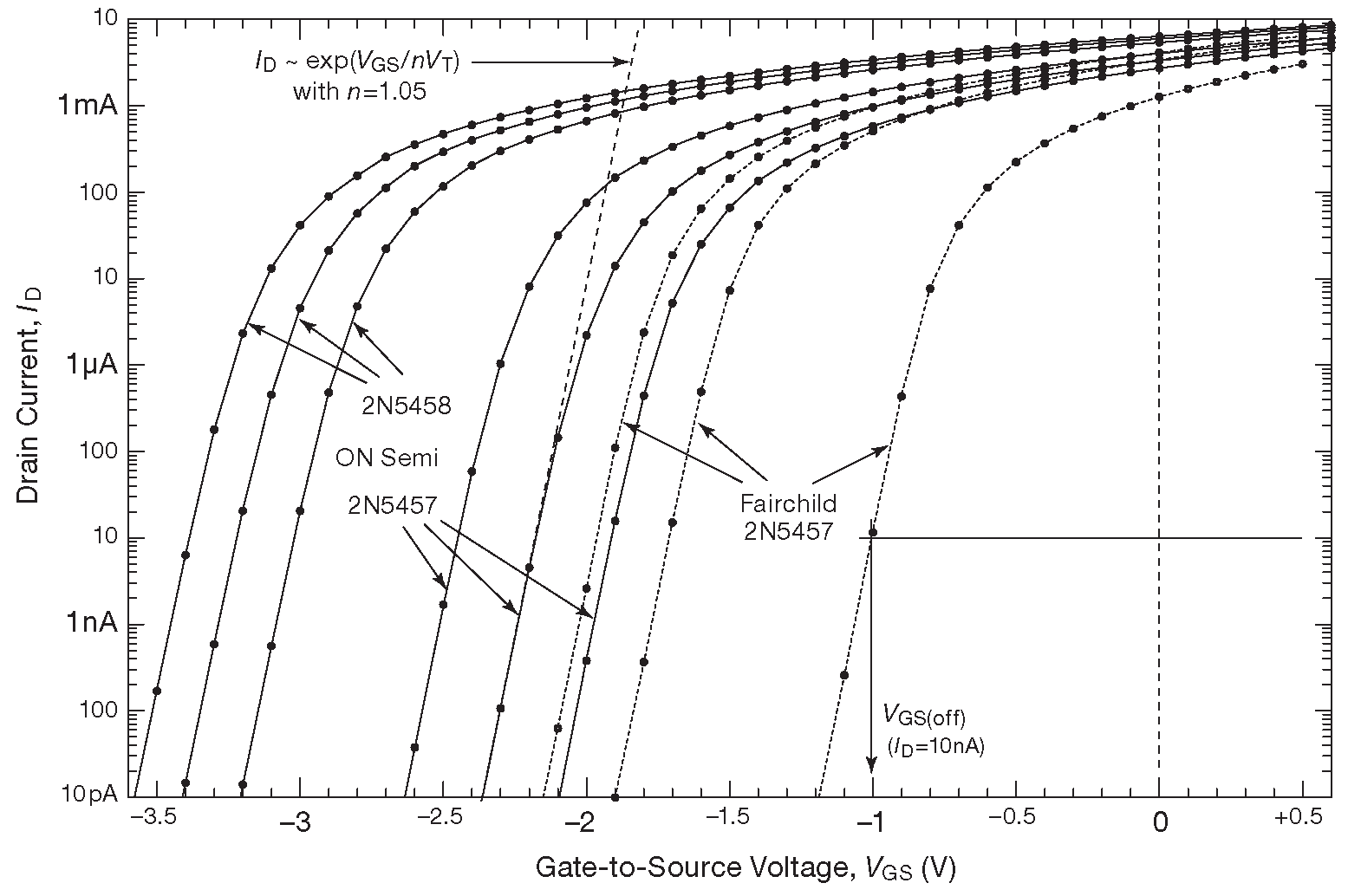
Рис. 3.52 Зависимость тока стока от напряжения на затворе для тех же ПТ, что и на рис. 3.51 по результатам измерения. Видно, что транзисторы отлично работают при токах стока 10 pA , которые гораздо меньше 10 nA , которые обычно указывают в качестве целевого для напряжения отсечки $V_{GS(OFF)}$

3.3.1.C Глубокая подпороговая область

Продолжение кривых, видимое на рис. 3.52 , показывает, что ПТ продолжают движение в том же направлении вглубь вплоть до пикоамперных токов стока, точно соответствуя экспоненциальному закону ( аналогично уравнению Эберса-Молла для биполярных транзисторов ), который можно записать в виде: \[ I_D = I_0·\exp \Bigg[\frac{V_{GS}}{nV_T}\Bigg] \quad . \qquad \qquad \qquad [3.12] \]

$V_T$ здесь - та же самая величина, что и в уравнении Эберса-Молла $V_T=kT/q$≈25mV , но с поправочным коэффициентом n . Данные измерений на рис. 3.52 соответствуют близкому к единице n ( n=1.05 ). Другими словами, на очень низких токах стока полевые транзисторы имеют ту же крутизну, что и биполярные, работающие с такими же токами коллектора ⁵⁸, что подтверждают результаты измерения крутизны на рис. 3.54 ( стр. 168 ). Отметим, что на низких токах у компонентов Fairchild наклон характеристики ( крутизна ) такой же, как и у прочих образцов. Теперь они не чемпионы по крутизне, как это было в квадратичном регионе, и ничем не отличаются от прочих.

3.3.2 Зависимость тока стока от напряжения сток-исток - выходная проводимость

Ток стока при постоянном $V_{GS}$ имеет некоторую зависимость от напряжения сток-исток, что несколько отличается от идеализированной картины, которую можно обычно видеть ( в распространении которой приняли посильное участие в том числе и §3.1.4 и рис. 3.13 ). Картина аналогична эффекту Эрли в биполярных транзисторах ( см. ##§X2.8 ) или, что то же самое, как конечный выходной импеданс $r_o$ ( или чаще употребляемый термин выходная проводимость $g_{os}$=1/$r_o$ ), который виден на выводе стока при постоянном напряжении затвор-исток. Он ограничивает максимальный коэффициент передачи в усилителе с заземлённым истоком и источником тока в качестве стоковой нагрузки ( это параметр Gmax в табл. 3.1 на стр. 141 ). Данный эффект надо учитывать, если требуемое усиление близко к Gmax , т.к. он ограничивает параметры истокового повторителя, если Gmax равно или меньше $g_mR_L$ ( а эти параметры уже и без того подпорчены низкой величиной произведения $g_mR_L$ , см. §3.2.6 ). Все перечисленные следствия подробно разбираются в Части X3 ( ##§X3.4 ), но важны в достаточной мере, чтобы быть упомянутыми здесь.

==167

3.3.2.A Снижение коэффициента передачи и линейности в усилителе с общим истоком

Описанный «эффект $g_{os}$» ограничивает максимальный коэффициент передачи усилителя с общим истоком за счёт появления сопротивления $r_o$=1/$g_{os}$ , параллельного импедансу нагрузки в стоке. Для простой резистивной нагрузки $R_D$ коэффициент передачи уменьшается с идеального значения G=$g_mR_D$ до G=$g_m(R_D||r_o)$ или \[ G=g_mR_D\frac{1}{1+g_{os}R_D} \quad . \qquad \qquad \qquad [3.13] \]

Другим незваным следствием является некоторая нелинейность, имеющая причиной зависимость $g_{os}$ от напряжения на стоке. См. ##§X3.4, если интересны подробности.

3.3.2.B Ошибка усиления в истоковом повторителе

«Эффект $g_{os}$» снижает усиление в истоковом повторителе, отдаляя его от идеального значения G=1 . Проблема особенно заметна на относительно низких нагрузках $R_L$≫1/$g_m$ , т.е. именно тогда, когда ожидается очень близкое к единице значение. Если учитывать данное явление, то формула усиления простого повторителя с рис. 3.40 выглядит так: \[ G=\cfrac{1}{1+\cfrac{1}{g_mR_L}+\cfrac{1}{Gmax}} \quad , \qquad \qquad [3.14] \]

где Gmax - отношение проводимости стока к крутизне ( Gmax=$g_{os}/g_m$ ) при заданном рабочем напряжении и токе. Эта величина почти не зависит от тока ⁵⁹ и поэтому удобнее, чем $r_o$ и $g_m$ , которые от тока зависят. Таким образом, чтобы ошибка усиления была меньше 1% и $g_mR_L$ , и Gmax должны быть больше 100 , либо нужны иные приёмы: активная нагрузка, каскод или «улучшитель крутизны». Можно возвратиться к учебному истоковому повторителю с рис. 3.43 и причинам, приведшим к появлению в варианте 3.43H активной нагрузки и каскода. Результаты измерения Gmax для распространённых ПТ можно найти в табл. 3.1 . Дополнительные материалы представлены в ##§X3.4.

==168

3.3.3 Крутизна как функция тока стока

Крутизна - естественная мера усиления полевых транзисторов. Выражается как отношение изменения тока стока к изменению напряжения затвор-исток ( $g_m≡i_D/v_{GS}$ ). В этом она аналогична модели Эберса-Молла для биполярных транзисторов, где $g_m=qI_C/kT=I_C/V_T$ . В общем случае, для любой величины тока крутизна ПТ будет ниже, чем биполярного. Начиная с самых низких токов ( §3.3.1 и рис. 3.52 ) крутизна ПТ в подпороговой области пропорциональна току стока, как в биполярных приборах, но несколько ниже, чем в последних, работающих при том же токе, см. рис. 3.53 . Если использовать форму $g_m=I_D/nV_T$ , то для типичного ПТ n будет лежать в диапазоне от 1.05 до 3 , что видно по экспериментальным данным на рис. 3.54 ( и аналогичных графиках в Части X3 , см. ##§X3.2 ).

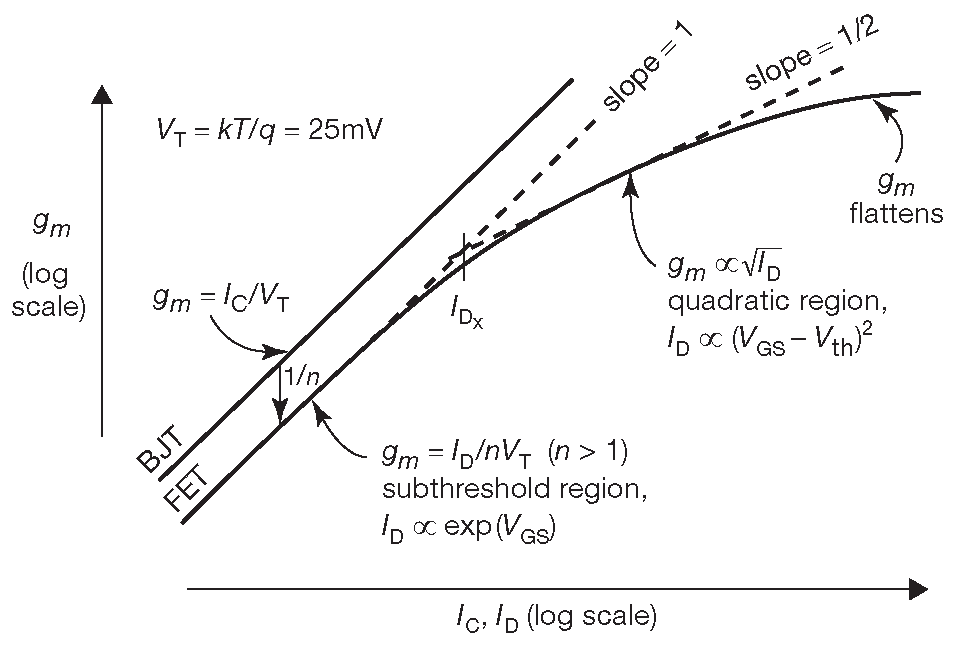
Рис. 3.53 Крутизна, как функция тока стока. В подпороговой области крутизна ПТ пропорциональна току стока ( как в биполярных приборах ). При нормальных токах, где $I_D∝(V_{GS}-V_{th})^2$ , крутизна пропорциональна уже $\sqrt{I_D}$ . Если же ток ещё выше [* при токовом насыщении ] , то крутизна плавно переходит к почти постоянному максимальному значению

При более высоких токах стока в «квадратичной области», где $I_D∝(V_{GS}-V_{th})^2$ , крутизна пропорциональна квадратному корню из тока стока, продолжая всё сильнее отставать от биполярных транзисторов, у которых коэффициент пропорциональности сохраняется ( $∝I_C$ ). При ещё больших токах коэффициент пропорциональности падает ещё больше. Для полевых транзисторов с p-n переходом история на этом заканчивается. У МОП приборов можно поднять напряжение на затворе до получения постоянного максимального тока стока, и график крутизны начинает загибаться вниз, как, например, в LND150, функция передачи которого показана на рис. 3.9 .

Померить крутизну непосредственно не так уж сложно. Схему одного из методов, секретным ингриндиентом которой является каскод, фиксирующий потенциал на стоке, можно найти в ##§X3.3. Авторы использовали названную схему, чтобы промерить примерно 60 ПТ при токе стока от 1μA до 30 mA , увеличивающимся с шагом примерно 5× .

Рис. 3.54 показывает данные для крутизны по току стока для нескольких распространённых ПТ ⁶⁰. При более высоких токах крутизна становится пропорциональна квадратному корню из тока стока, т.е. пропорциональна $(V_{GS}-V_{th})$ . Снизу картина обрезана на 1μA , но графики четырёх образцов (верхние) уже глубоко в подпороговой области, где крутизна пропорциональна току.

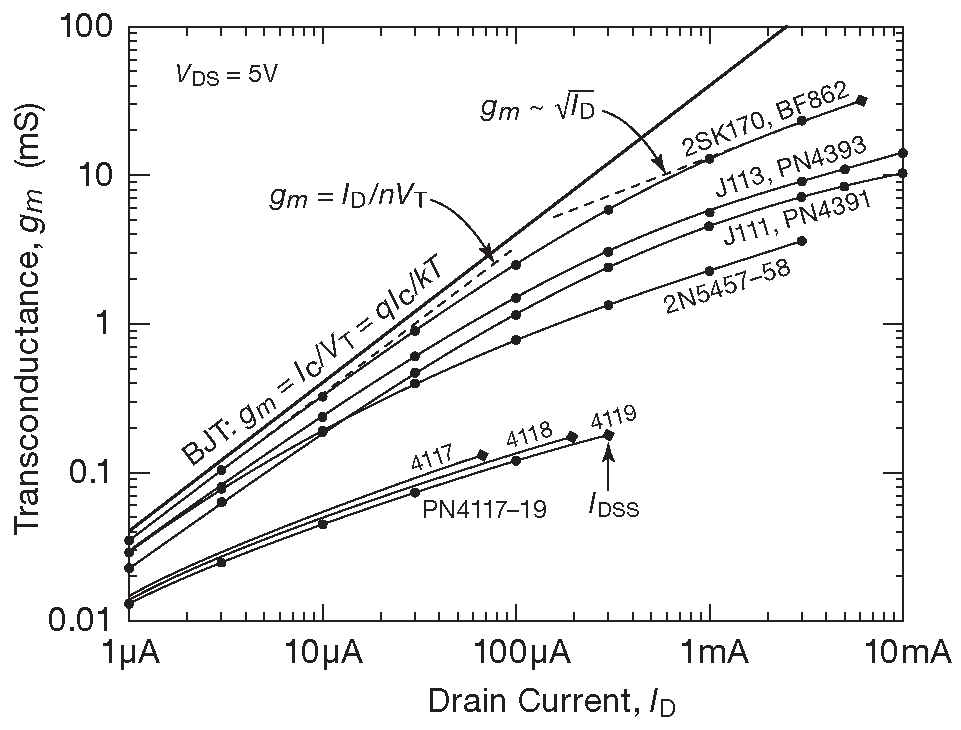
Рис. 3.54 Измеренное значение крутизны для некоторых типичных n-канальных ПТ, см. также аналогичный график в ##§X3.2

А что можно сказать от PN4117-19? Это очень маленькие ПТ ( что видно по их $I_{DSS}$ ), поэтому даже 1μA плотности тока уже достаточно, чтобы перевести их в квадратичную область. Иначе говоря, в предшествующей дискуссии стоило бы употреблять термин «плотность тока» ( а не просто «ток стока» ) в качестве меры для оценки нахождения в подпороговой или квадратичной области.

Отметим, что всё сказанное относится также и к МОП транзисторам. Мощные МОП приборы, нормированные на сотни ампер, будут работать в подпороговой области, если их ставить в линейные схемы ⁶¹. Как станет ясно из §3.6.3 , данное обстоятельство имеет важные следствия в вопросе температурной стабильности параллельного соединения МОП приборов. Дело в том, что в подпороговой области МОП транзисторы имеют положительный температурный коэффициент тока стока, что может привести к серьёзным неприятностям, если не будет учтено разработчиком.

==169

3.3.3.A Разброс по крутизне внутри семейства ПТ

Из предыдущего материала должно быть ясно, что предсказать крутизну при конкретном значении рабочего тока нельзя. Графики на рис. 3.54 дают разброс по крутизне $g_m$ 50:1 . Ситуация на самом деле ещё хуже. Данные на рис. 3.51 показывают, что невозможно даже примерно предсказать с хоть сколь-нибудь приемлемой точностью рабочий ток при конкретном смещении затвора ( и наоборот ) для конкретного типа транзистора.

Как оказывается ситуация не так безнадёжна. Внутри отдельного семейства ПТ крутизна зависит в основном, причём предсказуемо, от тока стока, даже если соответствующие потенциалы затвора могут быть каким угодно. Рассмотрим рис. 3.55 , на котором приведены результаты измерения тока стока для семи случайно выбранных 2N5486 ( с разницей дат 35 лет ⁶² ), нескольких экземпляров слаботочных родственников ( 2N5484, 2N5485 ) и похожего SST4416 ( он также рекомендуется для радиочастотных схем, имеет близкую ёмкость и сравнимый диапазон $I_{DSS}$ ).

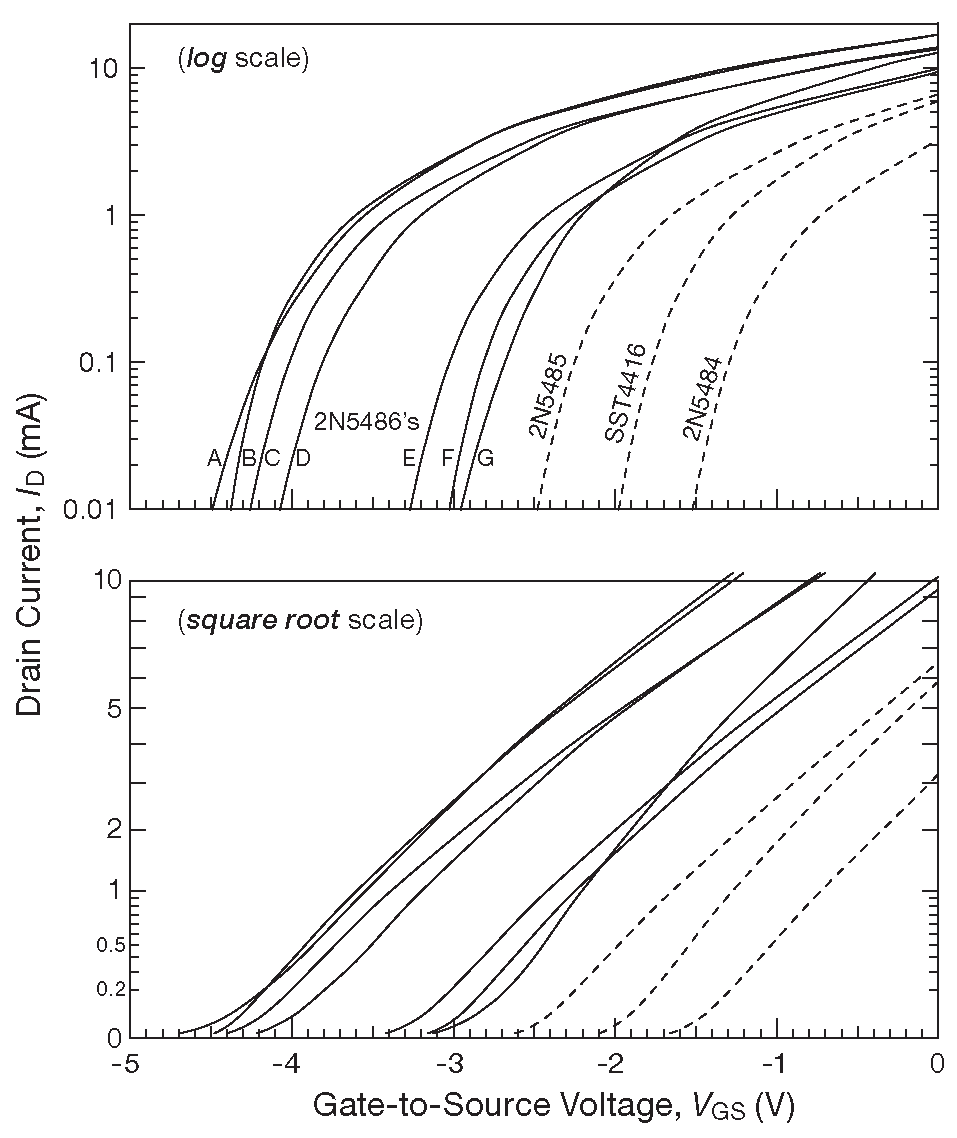
Рис. 3.55 Зависимость тока стока от напряжения затвор-исток для семи 2N5486 разной свежести и разных производителей ( и ещё трёх других ПТ, отмеченных пунктиром ) по результатам измерения. Графики масштабируются в виде логарифма и квадратного корня. Виден широкий разброс напряжения $V_{th}$ ( экстраполяция нижних концов кривых перед нижним изгибом прямыми линиями ). Данные графики можно сравнить с рис. 3.56 , где тот же набор ПТ слабо отличается крутизной по току стока

Кривые имеют широкий разброс по экземплярам ( диапазон 3:1 по $V_{GS(OFF)}$ и 5:1 по $I_{DSS}$ ), намекая на аналогичную непредсказуемость для транскондуктивного усиления ⁶³. Но обещание вводит в заблуждение. Измерение крутизны даёт график на рис. 3.56 . В случайном наборе из 10 экземпляров цифры показывают максимальную разницу при заданном токе стока не более ±20% .

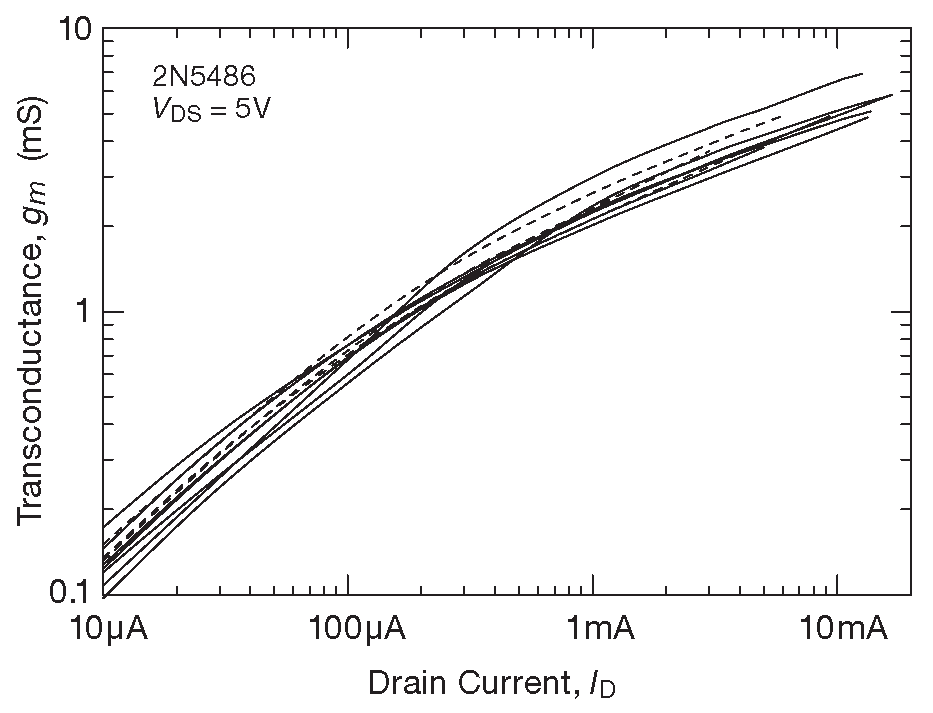
Рис. 3.56 Результаты измерения зависимости крутизны от тока стока для того же набора ПТ, что и на рис. 3.55

Мораль: внутри группы приборов со сходными характеристиками ток стока ( при каком-то напряжении на затворе, требуемом для такого тока ) является разумным ориентиром для оценки крутизны. Практическое следствие: усилитель на ПТ будет иметь более-менее предсказуемый коэффициент передачи, если имеет обратную связь, следящую за рабочей точкой и удерживающую заданную величину тока стока. Ток не должен превышать минимальное значение $I_{DSS}$ , иначе придётся проводить входной отбор.

==170

Немного жизненного опыта. Для уменьшения неопределённости усиления в схеме на ПТ будет разумно придерживаться одного из подходов.

Использовать истоковую дегенерацию ( ##§X3.4 ), желательно в связке с какой-нибудь схемой улучшения крутизны. Или
обеспечить нужную точность с помощью цепи общей обратной связи с достаточным минимальным петлевым усилением, т.е. для наихудшего значения $g_m$ ( как на рис. 3.31 , 3.34 и 3.37 ).

3.3.4 Крутизна как функция напряжения на стоке

Крутизна ПТ при заданном токе стока относительно независима от напряжения на стоке, исключая область $V_{DS}$ в пределах одного-двух вольт. И наоборот, наблюдается сильная зависимость от тока стока. См. обсуждение темы и данные измерений в Части X3 ( ##§X3.2 ).

3.3.5 Ёмкости ПТ

Подобно биполярным транзисторам ( и МОП, куда без них ) в ПТ есть ёмкость между выводами, которая зависит от обратного смещения. Она зовётся «нелинейной ёмкостью» и сильно снижается с увеличением обратного смещения. На рис. 3.57 показаны найденные в справочных данных графики ёмкости обратной связи и входной ёмкости двух распространённых n-канальных моделей. Приведённые величины - всего несколько пикофарад - типичны для малосигнальных ПТ и несколько меньше, чем можно найти в мощных МОП транзисторах ( сравните с рис. 3.100 на стр. 197 ). ПТ с p-n переходом обычно симметричны, но за счёт большего обратного смещения ёмкость сток-затвор меньше, чем затвор-исток ⁶⁴. Но это хорошо, т.к. эффект Миллера умножает $C_{RSS}$ в усилителе с общим истоком без каскода.

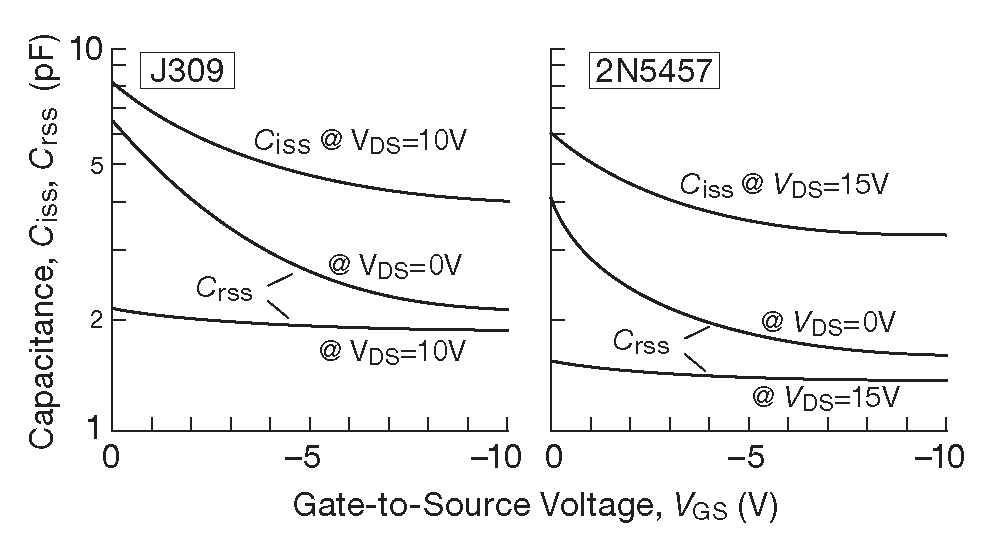
Рис. 3.57 Входная ёмкость и ёмкость обратной связи ПТ с переходом

Производители обычно приводят график зависимости ёмкостей от $V_{GS}$ и иногда ещё от $V_{DS}$ или $V_{DG}$ . Но на всё семейство предлагается только один набор кривых на всё семейство, притом даже, что спецификации $I_{DSS}$ легко могут отличаться на порядок и более. Получается, что, если ёмкости коррелируют с $I_{DSS}$ , то предлагаемые графики можно рассматривать только как грубую оценку реального положения вещей.

3.3.6 Преимущества усилителей на ПТ с p-n переходом по сравнению МОП вариантами

Изрядное место данной части отведено полевым транзисторам с p-n переходом - теме, мало освещаемой в литературе. А основной упор в публикациях делается на МОП приборы, т.е. транзисторы с изолированным затвором, и на то есть серьёзные причины. МОП транзисторы доминируют в следующих областях:

низковольтовые и малопотребляющие аналоговые устройства ( ОУ, портативная электроника, радиочастотные устройства и т.п. ),
аналоговые ключи,
логические схемы, микропроцессоры и память,
в виде дискретных транзисторов в сильноточных ключах и мощных линейных схемах.

Всё это актуальные направления развития современной электроники и МОП транзисторы с огромным отрывом лидируют на планете по размерам популяции.

Перед тем, как перейти к рассмотрению МОП приборов, будет полезно подчеркнуть, что ПТ с переходом - основной выбор для построения аналоговых устройств, требующих высокого входного импеданса, низкого шума и хорошей точности. Плюс на ПТ делаются двухвыводные источники тока, резисторы, управляемые напряжением и аналоговые ключи с постоянным сопротивлением канала $R_{ON}$ .

В примерах усилителей, повторителей и источников тока было показано много разных представителей ПТ. Базовые сведения дополняются материалом Части X3 , а в Части _8 разбирается шум полупроводниковых приборов. Чтобы дать представление об этих материалах, на рис. 3.58 приведены результаты измерения низкочастотного шума трёх фаворитов массового сегмента - биполярного npn 2N3904, ПТ с переходом 2N5457 и МОП 2N7000. Эти полупроводники не претендуют на премиальный сегмент, стОят копейки ⁶⁵ и не предназначены для малошумящих схем. На графике виден важный факт: МОП транзисторы сильно шумят на низких частотах, опережая биполярные и полевые транзисторы на 40 dB ⁶⁶. Не используйте их в малосигнальных трактах звуковой частоты. Зато мощные МОП транзисторы можно ставить в выходные каскады звуковых усилителей мощности.

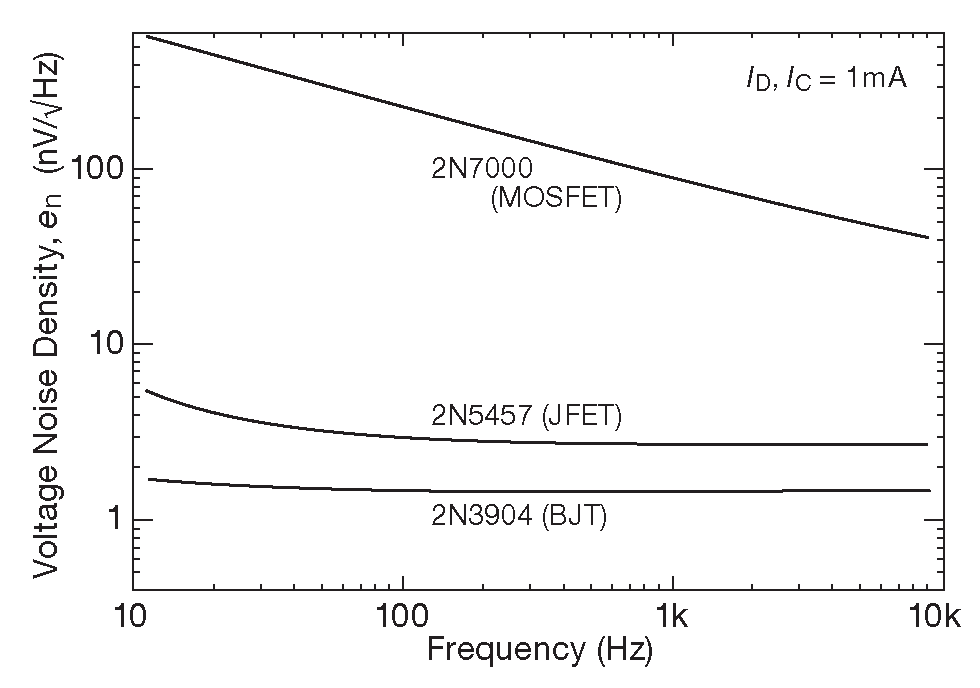
Рис. 3.58 Шумовое напряжение трёх полупроводниковых хитов выявляет плохие шумовые данные МОП транзисторов на низкой частоте

==170

⁵⁵ Термин «насыщение» может ввести в заблуждение. В случае ПТ он используется для обозначения токового насыщения. Это область напряжений на стоке, превышающих примерно вольт, при которых ток остаётся почти постоянным [* не реагирует на изменение этого самого напряжения на стоке ] . В биполярных транзисторах термин «насыщение» описывает напряжение насыщения ( состояние полностью открытого ключа ) в котором напряжение на коллекторе близко к нулю. Некоторые пояснения никогда не помешают, хотя делают их редко. [* См. Приложение AoE2_G ] . <-

⁵⁶ См. также шумовые параметры в табл. 8.2 . Таблица полевых транзисторов венчает несколько месяцев работы по сравнению спецификаций, проверки наличия на складах и лабораторных измерений. Авторы считают её весьма показательной и ценной и выражают надежду, что читатель воспользуется результатами. <-

⁵⁷ Компоненты фирмы Fairchild отмечены пунктирными линиями для большей заметности. <-

⁵⁸ Вот только полоса пожиже! К примеру, при токе $I_D$=10 pA произведение усиление-полоса $f_T$ в 2N5457 составит жалкие 140Hz ( $f_T=g_m/(2πC_{ISS})$ , см. «Полоса каскода, биполярные транзисторы в сравнении с полевыми» в Части X3 ). Приятно узнать, что полевые транзисторы, подобно биполярным хорошо работают при очень малых токах, что очень ценное свойство для малопотребляющих схем. Но не стоит забывать, что емкости переходов при низких токах угрожающе растут, поэтому при малых токах схемы работают медленнее, чем при больших. <-

⁵⁹ Если приглядеться, оба параметра и $g_m$ , и $g_{os}$ зависят от тока стока с приблизительным коэффициентом $\sqrt{I_D}$ ( §3.3.3 , ##§X3.2 ). Их отношение Gmax довольно стабильно относительно тока стока, но пропорционально напряжению сток-исток ( §3.3.4 , ##§X3.4 ). <-

⁶⁰ Расширенная версия графика приводится в ##§X3.2. <-

⁶¹ Любителям SPICE стоит напрячься: модели мощных МОП транзисторов в подпороговой области практически бесполезны. <-

⁶² A, Intersil, date code 7328 (28-ая неделя 1973г.); B, Central Semiconductor, современные; C and E, Fairchild, date code BF44; D, Vishay SST5486, современные; F, Vishay, date code 0536; G, Motorola, 1990г. <-

⁶³ Есть удобная зависимость: пороговое напряжение затвора $V_{th}$ выводится из тока при нулевом смещении $I_{DSS}$ . <-

⁶⁴ Под «стоком» и «истоком» подразумеваются выводы компонентов, выполняющие в схеме указанную функцию, а не снабжённых указанной маркировкой на выводах. [* Канал сток-исток полевого транзистора - симметричен и любой вывод может служить стоком ( хотя технология изготовления задаёт некоторую разницу в емкостях между выводами, см. §3.1.3 ] . <-

⁶⁵ Примерно $0.02, $0.05 и $0.04 соответственно в партии по 1000 шт. <-

⁶⁶ Согласно Джону Виллисону ( John Willison ) данное явление можно связать с кратковременным захватом и освобождением носителей заряда в изолированном затворе. <-