14.8 Форматы чисел
==1046
Разумнее всего завершить данную часть небольшим экскурсом в форматы чисел, имея в виду те из них, которые используются в арифметических устройствах компьютеров или при обмене данными с внешними устройствами. Общая картина видна на рис. 14.51 , а пояснения даны ниже.
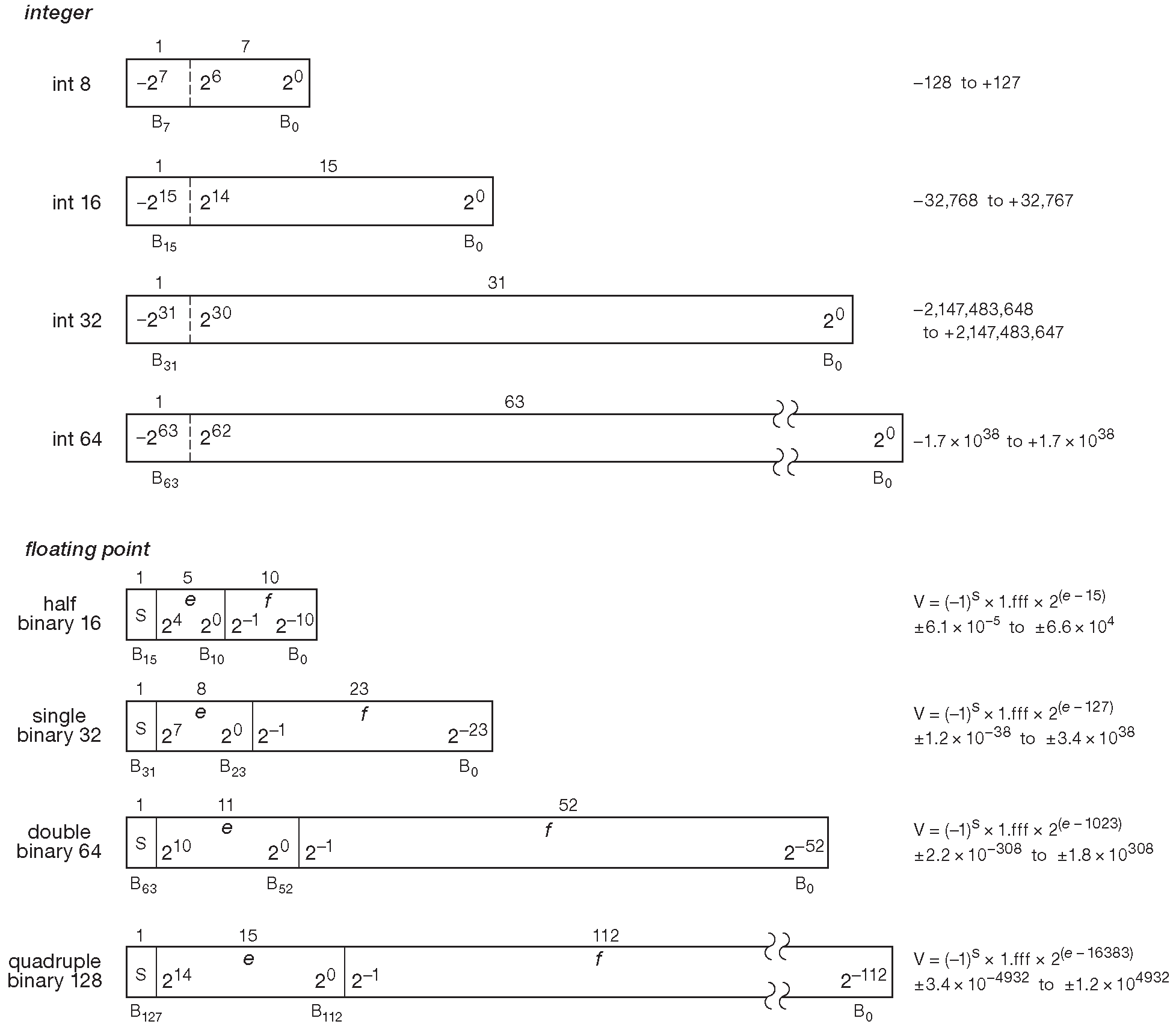
Рис. 14.51 Наиболее распространённые форматы чисел. Символом «e» обозначается экспоненциальная часть формата с плавающей запятой - показатель степени числа 2 ( беззнаковое двоичное целое [* ] ), на которое надо умножить мантиссу «f», чтобы получить число.
[* Так в оригинале, что согласуется с формулой получения числа справа, но правильнее назвать его, «модифицированный двоичный со смещением», см. §13.1.2 , а «модифицированный» ради ненормализованных чисел, см. ниже ]
14.8.1 Целые числа (Integers)
Целые числа со знаком всегда представляются в виде дополнения до 2 , и используют 1, 2, 4 и иногда 8 байт ( см. рис. 14.51 ). Дополнение до двух не то же самое, что представление «знак-величина», хотя в обоих форматах знак располагается в старшем значащем бите ( MSB ). Пример: «–1» в формате «знак-величина» 10000001b , а «дополнение до двух» 11111111b , см. §10.1.3 . Дополнение до двух можно рассматривать как двоичный код со смещением, у которого инвертирован старший ( знаковый ) разряд [* см. §13.1.2 . Кроме того, точно так же выглядят отрицательные числа: «–1» в виде дополнения соответствует –128 ] . Языки программирования позволяют объявлять переменные в виде целых без знака . Двухбайтовой целое без знака может принимать значения от 0 до 65536 .
==1047
Несколько в стороне от формата представления лежат проблемы размещения чисел в машинных словах разной разрядности. Например, двоичное целое на выходе АЦП должно быть выровнено по правому краю, чтобы числа увеличивались от 0 до величины полной шкалы ( от 0 до 4095 для 12-разрядного АЦП ). Но можно выровнять значение по левому краю и рассматривать число как часть целого [* где «целое» - значение полной шкалы, которое при таком рассмотрении становится единицей. Собственно величина получается умножением «доли целого» на значение этого «целого», т.е. на опорный потенциал, но делать это можно на каком-то из последующих этапов, чтобы не переполнять раньше времени разрядную сетку ] . Преимущество такого формата в том, что если разрешение АЦП увеличить [* во многих микроконтроллерах можно переключать разрешение АЦП между значениями 8–10–12 разрядов ] , то это будет выглядеть как появление дополнительных младших разрядов в дробной части, а не как увеличение шкалы измерения.
14.8.2 Формат с плавающей запятой (Floating-point)
Числа с плавающей запятой ( они же вещественные ) - наиболее распространённая форма представления величин в вычислительной технике. Чаще всего используются 32-разрядные ( однократной точности ) и 64-разрядные ( двойной точности ) представления 76 . Вообще, существует и используется несколько различных представлений чисел с плавающей запятой, но стандарт IEEE 754-2008 поддерживается практически всеми вычислительными устройствами.
==1048
Формат чисел с плавающей запятой подробно расписан на рис. 14.51 . Чтобы понять, как его надо воспринимать, рассмотрим 32-разрядное представление. В 32 разряда входит 1 знаковый бит, 8 бит экспоненты и 23 бита дробной части - мантиссы. Экспоненциальная часть сообщает показатель степени множителя ( 2 ), на который умножают мантиссу, чтобы получить число. «Нулём» для экспоненты служит число 127 , поэтому показатель экспоненты 01111111b соответствует множителю \(2^0\)=1 . Таким образом, показатель степени меняется от –127 до +128 . [* Стоит напомнить, что обычный «двоичный со смещением» кодирует числа от –128 до +127 ( §13.1.2 ), с нулём на «уровне» +128 ] . Дробная часть опирается на интересный приём, впервые использованный фирмой DEC в своём формате чисел с плавающей запятой. Такие числа всегда записывают в форме «f.fff×2e», где «f.fff» - мантисса – «значащая» часть, записанная в двоичном формате, а «e» - экспонента. Чтобы увеличить точность при заданной разрядности мантиссы, над числами надо проводить операцию «нормализации»: сдвигать мантиссу влево и соответственно уменьшать экспоненту [* для мантиссы - операция «сдвиг влево», эквивалентная «умножению на 2», а для экспоненты - операция «–1», сдвигать её нельзя ] , пока самый старший разряд не примет ненулевое значение [* все лидирующие нули отброшены ] , т.е. примет форму «1.fff×2e». А теперь фокус! В результирующем числе старший бит всегда имеет единичное значение, поэтому можно прекратить тратить на него место в памяти, но продолжить учитывать при вычислениях, т.е. число «1.fff» в памяти будет храниться в виде «fff», а лидирующая единица лишь подразумевается. В итоге получаем увеличение точности при том же диапазоне значений.
Упражнение 14.3
Покажите, что диапазон нормализованных чисел соответствует заявленному ( рис. 14.51 ), для чего соберите наибольшее и наименьшее число в описанном формате.
Формат двойной точности строится аналогично, но за счёт 29 дополнительных разрядов мантиссы имеет существенно большую точность, а 3 дополнительных разряда экспоненты расширяют диапазон чисел. Некоторые любят по-длиннее и, если двойная точность вам по сердцу, то, возможно, понравится и формат учетверённой точности со 113 битами мантиссы и 15-разрядной экспонентой.
С другого конца недавно появился формат «половинной точности» ( иногда называемый «minifloat» ). В нём знак, экспонента и мантисса упакованы в 16-разрядное слово. Наибольшее число доступное в таком формате ±65504 . Это не сказать, чтобы много, если сравнить с диапазоном 16-разрядных знаковых целых ( ±32767 ). Формат кажется бессмысленным подражанием, но это не так. Наименьшее число в IEEE minifloat равно \(±6.1×10^{-5}\). Такой формат обеспечивает динамический диапазон , хотя точности и не прибавляет 77 .
Последнее утверждение требует некоторых пояснений. Формат половинной точности ( официальное название «binary16» ) способен представлять величины в диапазоне девяти порядков с примерно одинаковым шагом расстановки чисел ∼0.06% . В отличие от целочисленного представления для небольших значений точность представления не ухудшается ( объясните почему ), а это очень важная характеристика для величин, меняющихся по логарифмическому закону, таких как освещённость или громкость.
Формат IEEE позволяет использовать ненормализованные числа, что чуть расширяет диапазон вниз за счёт некоторого снижения точности. В данном режиме поле экспоненты заполнено нулями, что является признаком изменения вида мантиссы на 0.fff . Для формата однократной точности ( «binary32» ) диапазон денормализованных чисел доходит до \(±1.4×10^{-45}\) , но шаг изменения между соседними числами увеличивается по мере приближения к наименьшему значению. Стандарт определяет нуль ( e=0 и fff=0 , т.е. есть +0 и –0 ) и бесконечность ( e - все единицы, fff=0 , т.е. тоже обоих знаков ). Кроме того, есть т.н. «не числа» NAN , с помощью которых сообщается об особых ситуациях при расчётах.
14.8.2.A Хранение чисел в памяти
Разработчики микропроцессоров любят выказывать свою исключительность, меряясь методами хранения чисел в памяти. Процессоры с архитектурой Intel располагаю многобайтные целые, начиная с самого младшего байта величины и располагая его в памяти с наименьшим адресом. Motorola хранит числа в ровно обратном порядке 78 . Некоторые процессоры ( например ARM ) могут использовать оба варианта ( и получили название «bi-endian» ). Чтобы разнообразить картину и порадовать пользователя, некоторые процессоры используют один порядок для целых чисел и противоположный для вещественных. Данная тема - отнюдь не академические штудии: порядок имеет значение, когда данные передаются по внешним каналам, что неизменно вносит некоторое разнообразие в серые будни программистов.
==1048
76 В дополнение к ним идут укороченный 16-разрядный формат «половинной точности» и гигантский 128-разрядный «четырёхкратной точности». <-
77 Это характеристика, важная для некоторых областей, например, для работы с изображениями. Что характерно, фирма Industrial Light & Magic, предложившая данный формат, позиционировала его именно для такого использования. Числа половинной точности поддерживаются графическими сопроцессорами, которые всё активнее используются в масштабных вычислительных задачах. Графические сопроцессоры содержат на кристалле сотни мелких вычислительных ядер, создавая реальную конкуренцию обычным процессорам. Засунув в коробку несколько десятков таких микросхем можно организовать весьма производительный минисуперкомпьютер. <-
78 Инженеры не отстают, путая непосвящённых терминами «little-endian» и «big-endian» соответственно. <-

