H.4 Эпилог: вывод характеристического импеданса через лестничную цепь

==1127

На курсе электродинамики анализ ведётся в помощью преобразований Максвелла, и в результате получается зависимость между электрической \(\vec E\) и магнитной \(\vec B\) составляющими поля. Из них следуют соотношения между током и напряжением, т.е. импеданс. В качестве бесплатного приложения идёт индуктивность/ ёмкость на единицу длины и скорость распространения.

Но есть удобная «схемотехническая» форма, позволяющая удостовериться, что корректно согласованная линия выглядит как чисто резистивная с номиналом, равным «волновому сопротивлению». Её зовут «лестничная модель». Она собрана из дискретных LC элементов ( рис. H.17 ), каждый из которых относится к малому элементу длины линии \(\delta_x\) . Каждый такой элемент имеет последовательную индуктивность \(\mathscr L·\delta_x\) и шунтирующую ёмкость \(\mathscr C·\delta_x\) , где \(\mathscr L\) и \(\mathscr C\) - индуктивность и ёмкость на единицу длины линии. В полной линии таких элементов N=\(l/\delta_x\) .

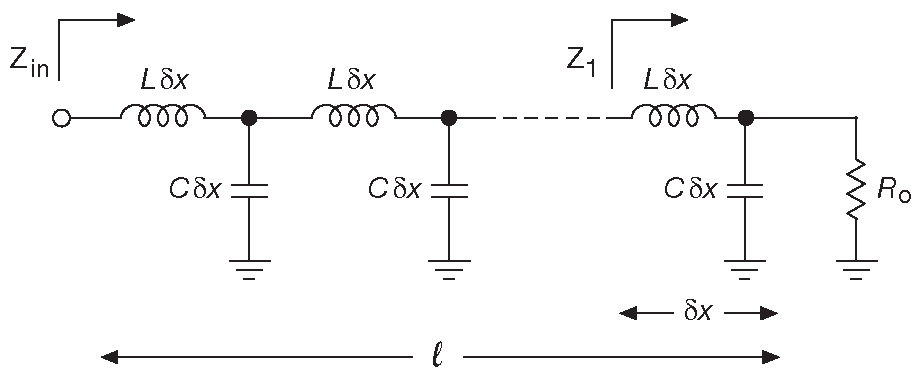
Рис. H.17 Лестничная модель линии передачи длиной \(l\) . Особый интерес представляет предел \(\delta_x\to 0\) , при котором число элементов N=\((l/\delta_x)\to∞\)

H.4.1 Первый способ: согласованная линия

Начнём ^_8 с расчёта импеданса линии со стороны последней секции ( \(Z_1\) на рис. H.17 ) и покажем, что отношение \(\mathscr{L/C}\) , выражающее \(Z\) , примерно равно \(R_0\) . Затем покажем, что импеданс всей линии сводится точно к \(R_0\) , как только будет произведена замена дискретного приближения на непрерывную модель линии передачи со стремящейся к нулю длиной каждого элемента \(\delta_x\) .

Итак. \(Z_1\) - просто импеданс цепи из \(\mathscr L·\delta_x\) , включённой последовательно с параллельным соединением \(R_0\) и \(\mathscr C·\delta_x\) . \[ Z_1=jω(\mathscr L·\delta_x)+\frac{R_0·\left (\cfrac{-j}{ω(\mathscr C·\delta_x)}\right )}{R_0-\cfrac{j}{ω(\mathscr C·\delta_x)}} = jω(\mathscr L·\delta_x) + \frac{R_0}{1+jω(\mathscr C·\delta_x)R_0} ≈ R_0+jω(\mathscr L-R_0^2\mathscr C )·\delta_x \]

На последнем шаге преобразования был взят только первый член ряда, т.е. \(\frac{1}{1+ε} ≈ 1-ε\) .

Второе слагаемое сократится после подстановки \(R_0 = \sqrt{{\mathscr L}/{\mathscr C}}\) , которая является формулой характеристического импеданса линии. Впрочем, не будем торопиться, т.к., если \(\delta_x\to 0\) , второе слагаемое сокращается в любом случае. Вместе со вторым слагаемым сокращается и вся линия передачи. Что надо сделать, ток это добавить члены ряда старших порядков и посмотреть, что будет, если \(\delta_x\) устремить к нулю, удерживая общую длину линии \(l\) постоянной. В этом случае растёт число элементарных участков N=\(l/\delta_x\) .

Читателю предоставляется почётное право сделать математические выкладки самостоятельно. В итоге должно получиться, что два следующих члена разложения ^_9 добавляют величины порядка \(\delta_x^2\) и \(\delta_x^3\) . При этом \(Z_1\) будет выглядеть как \[ Z_1 ≈ \left\{R_0+\mathscr O(\delta_x^2 )\right\} + j\left\{ω(\mathscr L- R_0^2\mathscr C )·\delta_x+\mathscr O(\delta_x^3 )\right\} \]

Значит, при каскадировании N секций ( где N=\(l/\delta_x\) ) с условием \(R_0 = \sqrt{{\mathscr L}/{\mathscr C}}\) элементы более высоких порядков по мере приближения \(\delta_x\) к нулю будут убывать как \(\mathscr O(\delta_x) \) для действительной части и \(\mathscr O(\delta_x^2) \) для мнимой. Таким образом, входной импеданс линии передачи длиной \(l\) , нагруженной на собственный характеристический импеданс \(R_0\) ( резистивный ), также резистивен и равен \(R_0\) .

H.4.2 Второй метод: полубесконечная линия

Вот ещё один способ ¹⁰, который не требует приближений и учёта взаимного влияния. Идея состоит в рассмотрении одного конца линии передачи на сосредоточенных элементах, продолжающейся в бесконечность ( рис. H.18 ). Отметим, что при движении вправо линия не изменяется. Назовём комплексный входной импеданс линии \(\mathbf{Z_0}\) , тогда имеем \[ \mathbf{Z_0}=jωL + \mathbf{Z_0∥Z_C} = jωL+ \frac{\mathbf{Z_0}·(-\frac{j}{ωC})}{\mathbf{Z_0}-\frac{j}{ωC}} \]

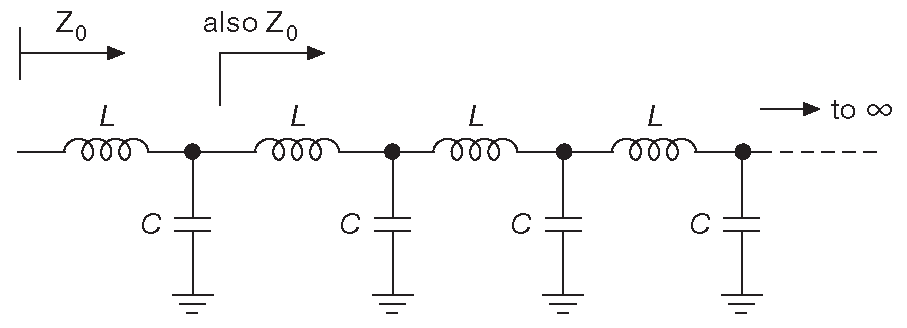
Рис. H.18 Полубесконечная лестничная LC модель позволяет упростить расчёты

==1128

Избавляемся от переменных в знаменателе, умножая уравнение на знаменатель последнего члена. После перегруппировки выражения получаем квадратное уравнение для \(Z_0\): \[ \mathbf{Z_0}^2 - jωL\mathbf{Z_0} - L/C = 0. \]

Его решение: \[ \mathbf{Z_0}=jωL±\frac{\sqrt{4\frac{L}{C}-ω^2L^2}}{2}. \]

Ну, и последний финт . Мы сокращаем длину каждого сегмента, оставляя общую длину неизменной. Каждая отдельная индуктивность и ёмкость стремится к нулю, но их отношение остаётся неизменным. Таким образом, остаётся только 4\(L/C\) и только действительная часть импеданса \(\mathbf{Z_0}=\sqrt{\frac{L}{C}}\) . И никаких приближений!

H.4.3 Послесловие: линия задержки на сосредоточенных элементах

Изобретательные проектировщики аналоговых осциллографов в старые тёмные времена ламповой электроники нашли способ получить горизонтальную развёртку до запускающего события, а именно: задержать отображаемый сигнал на 100 ns , с помощью линии задержки ¹¹. Проектировщики первых ламповых осциллографов ( например, легендарного Tektronix 545A ) использовали линию задержки на сосредоточенных элементах, подобную изображённой на рис. H.19 , чтобы придержать сигнал ( на 200 ns в данном случае ). А иначе потребовалось бы 30 m кабеля. Очевидно, инженеры с пользой применили теорию, изученную на курсе электротехники ¹². Позднее линии задержки из дискретных элементов были заменены коаксиальными кабелями с парой спиральных жил. За счёт большей индуктивности на единицу длины увеличилось время задержки ¹³ и характеристический импеданс. На фотографии видно кабель, закрученный бухтой вокруг ЭЛТ ¹⁴ на свободном месте в корпусе. На рис. H.21 показано внутреннее устройство красивой сдвоенной линии задержки. Спиральный проводник обеспечивает 36 ns/m , а на рис. H.22 линия показана в работе.

Рис. H.19 В аналоговом осциллографе входной сигнал проходит через линию задержки, которая позволяет наблюдать события, вызвавшие запуск развёртки. Модель 1959г. Tektronix 545A ( слева ) имела рабочую полосу 30 MHz и использовала двухканальную 200-наносекундную линию задержки на сосредоточенных элементах. Конструкция состояла из 50 пар катушек и 50 подстроечных (!) конденсаторов ( см. рис. H.20 ). Полупроводниковая модель 1982г. 2213 ( справа ) имела рабочую полосу 60 MHz и использовала 2.5m коаксиального кабеля со спиральной жилой в качестве задержки на 100 ns

==1129

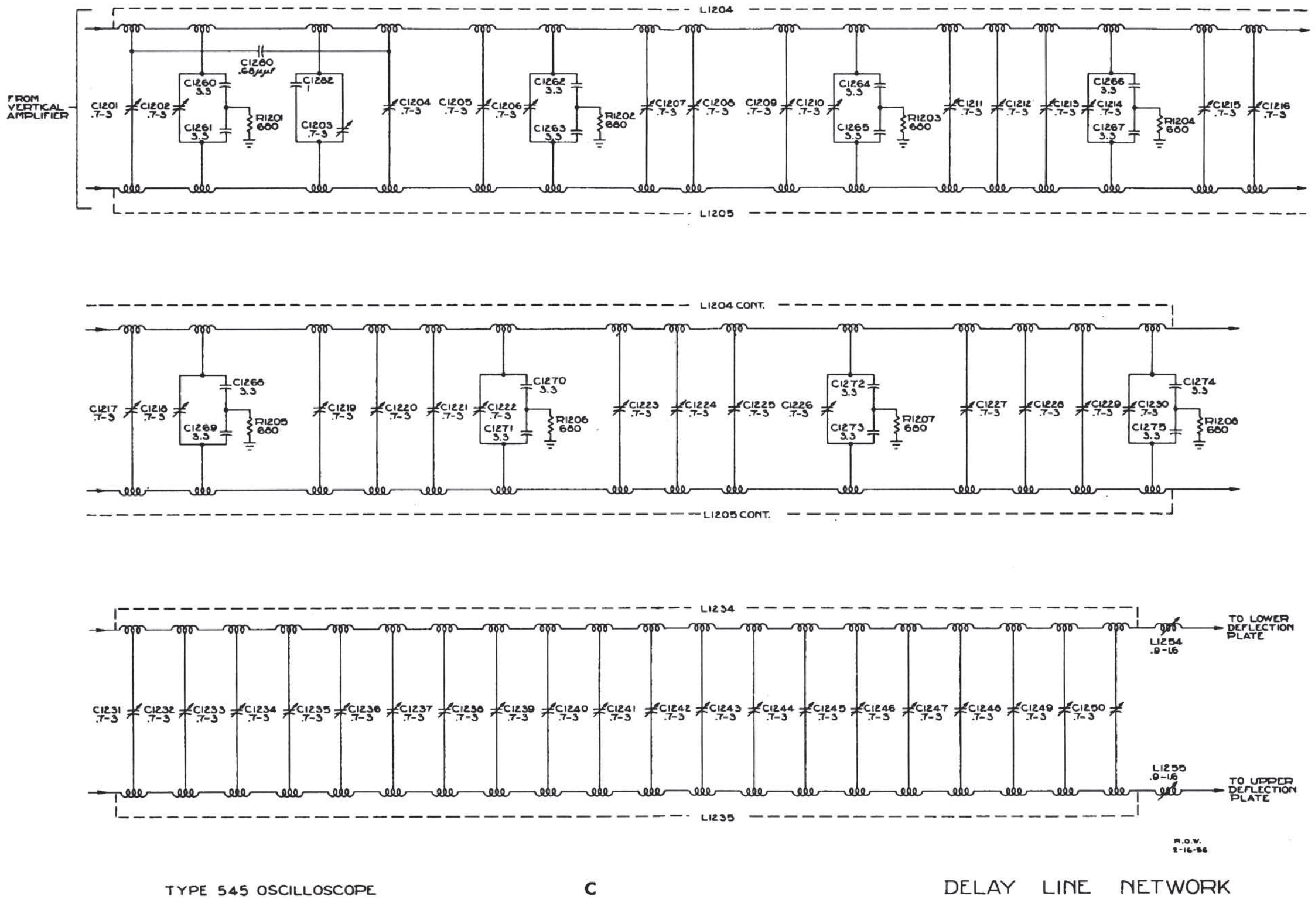
Рис. H.20 Трудный путь к совершенству. В 1950-х Tektronix использовал 50 пар катушек и 50 подстроечных конденсаторов, чтобы собрать линию задержки для своего осциллографа модели 545 ( см. рис. H.19 ). Воспроизводится с разрешения Tektronix Inc.

==1130

Рис. H.21 Авторы разобрали останки Tektronix 2213 и обнаружили внутри линию задержки на 100 ns . Её дифференциальный импеданс 155 Ω , а длина 2.5 m . Две центральные жилы калибра #30 намотаны на оправку диаметром 2 mm с шагом 1.25 mm . Экран имеет внутренний диаметр 3.25 mm

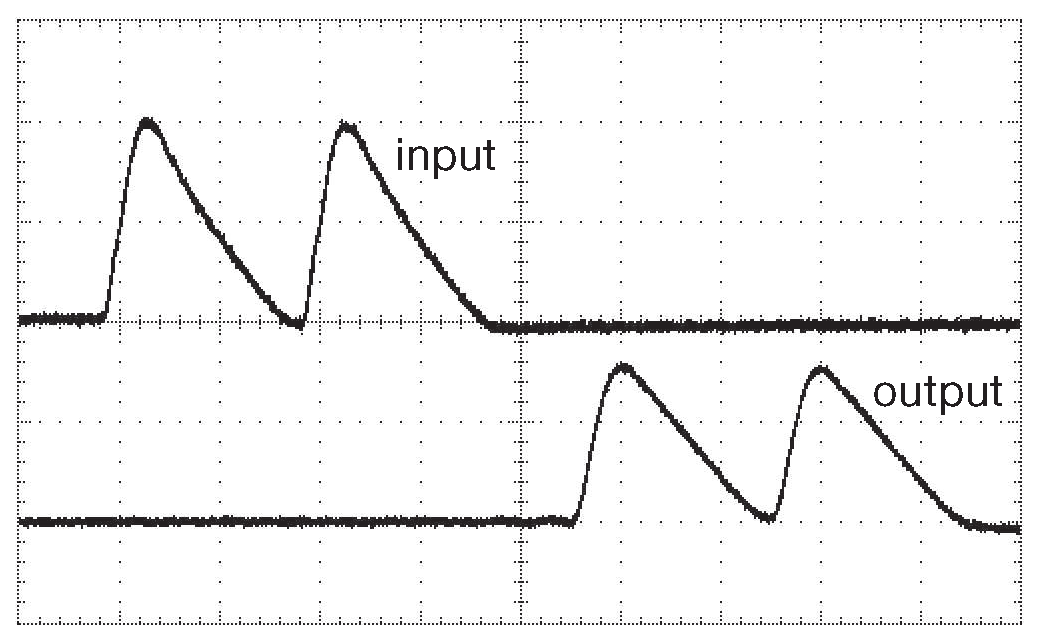
Рис. H.22 Сигнал, идущий по линии задержки с рис. H.21 , вернее, по тому, что от неё осталось. Задержка ∼95 ns . Качество сигнала очень хорошее, хотя тестовый сигнал имеет полосу более 60 MHz , на которые рассчитан осциллограф. По горизонтали 20 ns/div , по вертикали 1 V/div

==1130

⁸ Такое рассмотрение было предложено в Hagen “Radio Frequency Electronics” [78] , см. Приложение _N . <-

⁹ Они равны \(-R_0^3(ω·\mathscr C·\delta_x)^2+jR_0\space^4(ω·\mathscr C·\delta_x)^3\) , если хочется проверить вывод. <-

¹⁰ За авторством Г.Головченко. <-

¹¹ Цифровые осциллографы обходят эту проблему с помощью цифровой памяти, в которой хранятся результаты измерений, сделанных до срабатывания триггера. <-

¹² Конденсаторы из линии задержи на сосредоточенных элементах с рис. H.19 подключаются к средней точке каждой катушки, см. официальную документацию на рис. H.20 . По-видимому, такая конструкция эффективнее. <-

¹³ Примерно в π×n×D раз, где n - число витков спирали на единицу длины, а D - диаметр витка. Так как шаг спирали достаточно велик, и витки проходят близко от экрана, распространение сигнала можно рассматривать просто как движение по оси спирали, подобно движению штопора для бутылок. Такой подход позволяет упростить уравнения и обойтись без вычисления индуктивности и ёмкости на единицу длины. <-

¹⁴ Это электронно-лучевая трубка , чтобы было понятно тем, кто родился в этом тысячелетии и был лишён возможности пообщаться с ней лично. <-