Приложение F. Нагрузочные линии
==1112
Графический метод «нагрузочных линий» обычно встречается в начале учебников по электронике. Авторы решили обойтись без него, потому что этот метод хорош для электровакуумных приборов, но не так удобен при разработке транзисторных схем. Но, тем не менее, его используют при работе с некоторыми нелинейными компонентами ( например, туннельными диодами ), и, в любом случае, это один из инструментов разработки.
F.1 Пример
Начнём с примера. Пусть нам хочется узнать напряжение на диоде ( рис. F.1 ). Полагаем, что вольтамперная характеристика типичного диода известна ( конкретный экземпляр может иметь технологический «разброс» параметров, которые, к тому же, зависят от температуры ). Выглядит она примерно как на рисунке. Как найти интересующую _1 точку?
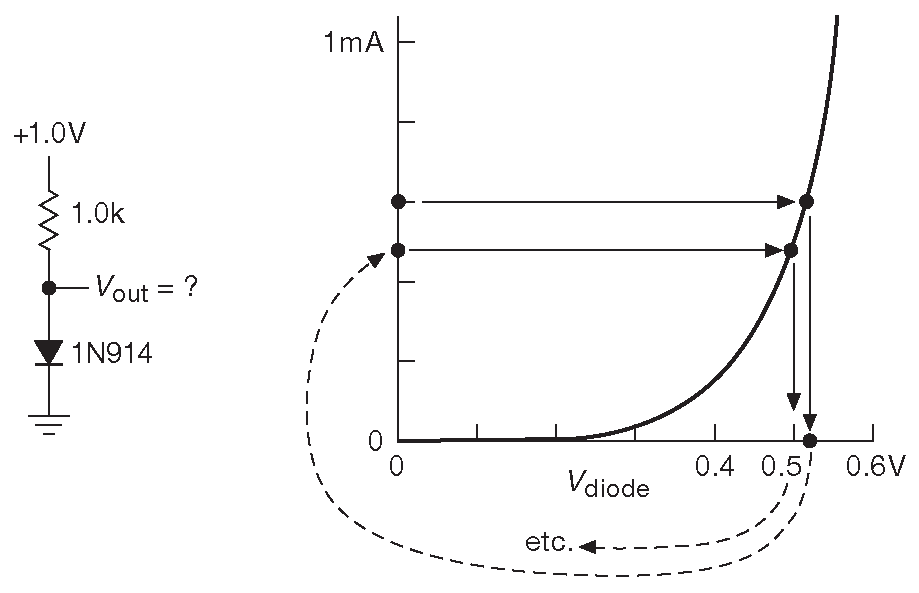
Рис. F.1 Последовательный поиск рабочей точки
Одним из методов является примерная оценка тока, скажем, 0.6 mA . Затем по графику выясняется падение на диоде, а значит, и резисторе, по которым можно уточнить ток ( здесь 0.48 mA ). Такой последовательный метод показан на рис. F.1 . После нескольких циклов можно получить ответ, но процесс оставляет желать много лучшего.
Метод нагрузочных линий позволяет получить ответ в такой задаче сразу. Предположим, в схеме F.1 вместо диода стоит какой-то прибор и 1.0 kΩ в качестве нагрузки. Построим график зависимости тока резистора от напряжения на двухвыводном приборе. Это легко. При падении на приборе 0V ток равен \( V_+/R\) ( всё напряжение падает на резисторе ). При падении на приборе \( V_+\) , ток через резистор отсутствует. Промежуточные значения попадают на прямую между этими двумя точками [* поэтому что резистор - линейный элемент ] . Теперь на том же графике надо нарисовать вольтамперную характеристику второго элемента. Рабочая точка принадлежит обоим графикам, т.е. лежит в точках их пересечения ( рис. F.2 ).
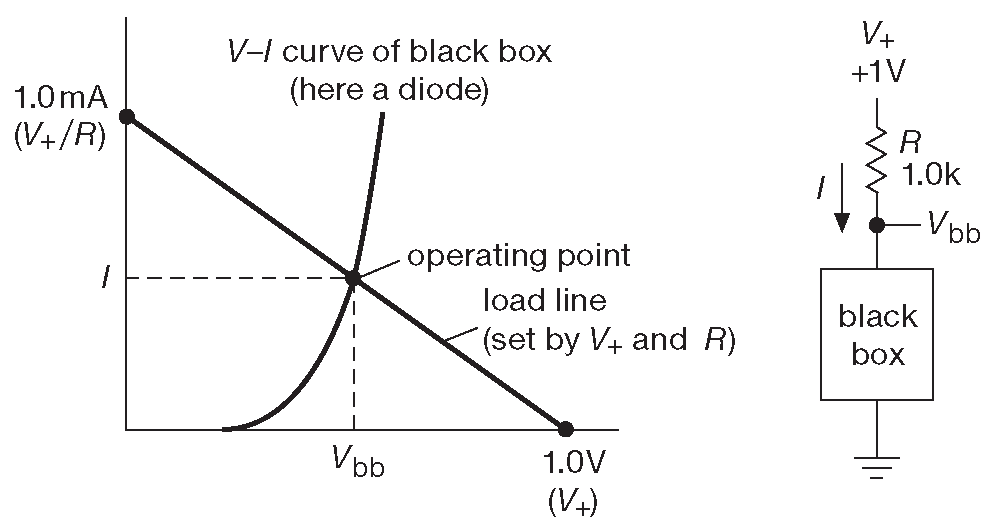
Рис. F.2 Метод «нагрузочных линий» позволяет найти рабочую точку непосредственно
F.2 Трёхвыводные устройства
Нагрузочные линии можно использовать и для трёхвыводных устройств, например, электронных ламп или транзисторов, надо только нарисовать семейство кривых для этих приборов. Рис. F.3 показывает, как это будет выглядеть для обеднённого полевого транзистора с графиками для разных напряжений затвор-исток. Получить выходные параметры можно, двигаясь вдоль нагрузочной линии, ограниченной кривыми, соответствующими входному сигналу и считывая нужные значения на осях. В данном примере показана картина для входного сигнала между 0V и –2V .
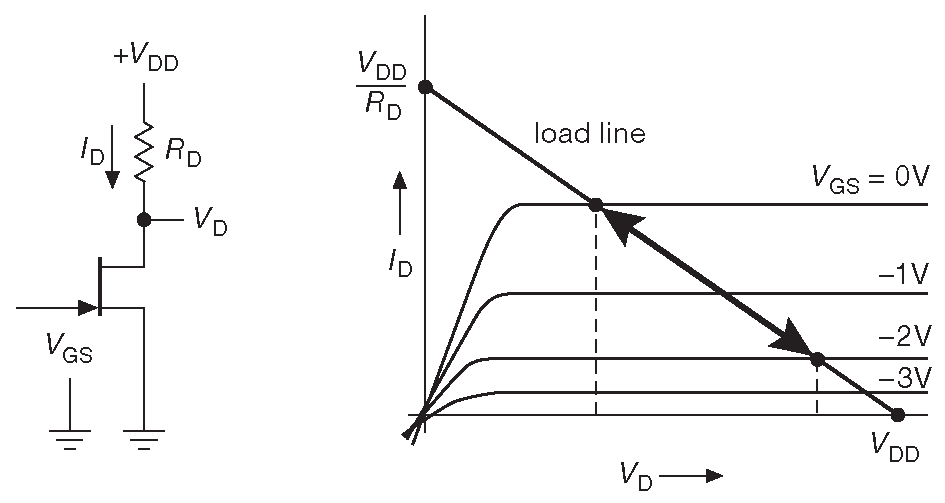
Рис. F.3 Метод нагрузочных линий для трёхвыводного прибора
==1113
Метод выглядит привлекательно, но мало помогает при работе с трёхвыводными полупроводниками по ряду причин. Во-первых, кривые в справочных данных рисуются производителем только для «типичных» значений, а разброс реальных цифр может быть пятикратный. Посмотрите, что станет с результатом, если все кривые сократятся в размерах в четыре раза. Во-вторых, для приборов с логарифмической характеристикой, как у p-n перехода, линейная форма нагрузочных линий даёт приемлемую точность только в узкой области. Наконец, аналитические методы, используемые в книге, полностью соответствуют практике работы с полупроводниками, а именно: они опираются на все поддающиеся учёту параметры ( \( r_e\) , зависимость \(I_C\) от \( V_{BE}\) и \( T\) и т.д. ), а не на характеристики, имеющие большой разброс ( \(β\) , \( V_{th}\) и т.д. ). В любом случае, использование метода нагрузочных линий с использованием графиков для типичных значений без указания их возможного разброса даёт ложное чувство уверенности в результате.
F.3 Нелинейные устройства
Зато нагрузочные линии удобны для понимания поведения сильно нелинейных устройств. Несколько интересных моментов может показать пример с туннельным диодом. Рассмотрим схему F.4 . Теперь место напряжения питания занимает входной сигнал. Графики построены для нагрузочного резистора 100 Ω , поэтому изменение входного сигнала порождает семейство параллельных нагрузочных линий [* для резистора ] , пересекающих вольтамперную характеристику прибора ( рис. F.5 ). Как легко видеть, быстрее всего выход меняется, когда входное изменение попадает в область отрицательного сопротивления на графике туннельного диода. Считывая значение \( V_{out}\) ( ось X ) для различных входных уровней ( отдельных нагрузочных линий ) [* в точках пересечения ] можно построить график функции передачи . Данная схема имеет область усиления по напряжению для входного сигнала около 0.2 V .
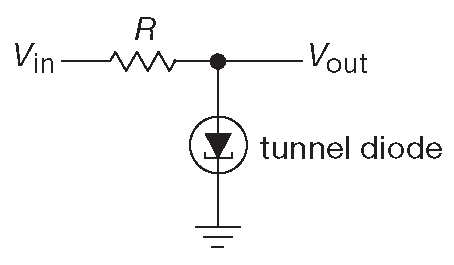
Рис. F.4 Туннельный диод - нелинейный двухвыводной прибор с областью отрицательного сопротивления, см. рис. F.5
Самое интересное происходит, если нагрузочные линии идут положе, чем центральная секция вольтамперной характеристики диода. Это случается, когда нагрузочное сопротивление превышает размах отрицательного сопротивления диода. В этом случае появляется две точки пересечения графиков ( рис. F.6 ). Возрастающий сигнал на входе следует вдоль нагрузочной линии до первой точки пересечения, непонятно куда исчезает и вновь появляется, когда сигнал достигает второй точки \( V_{out}\) . В обратном направлении напряжение идёт до верхней точки пересечения и проваливается до второй точки, где возникает вновь. На графике функции передачи появляется область гистерезиса . Туннельные диоды использовались в качестве быстрых переключательных устройств ( триггеров ).
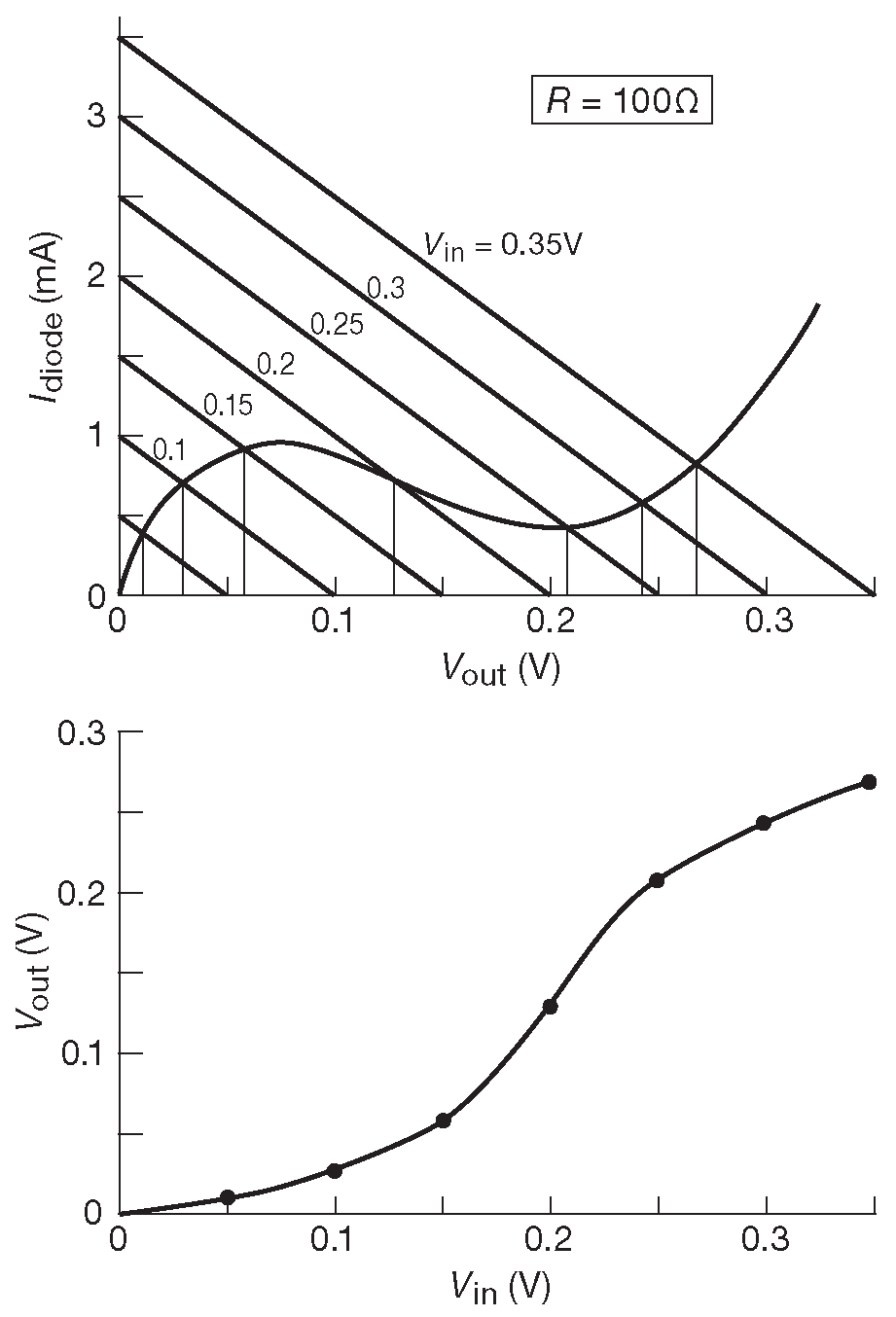
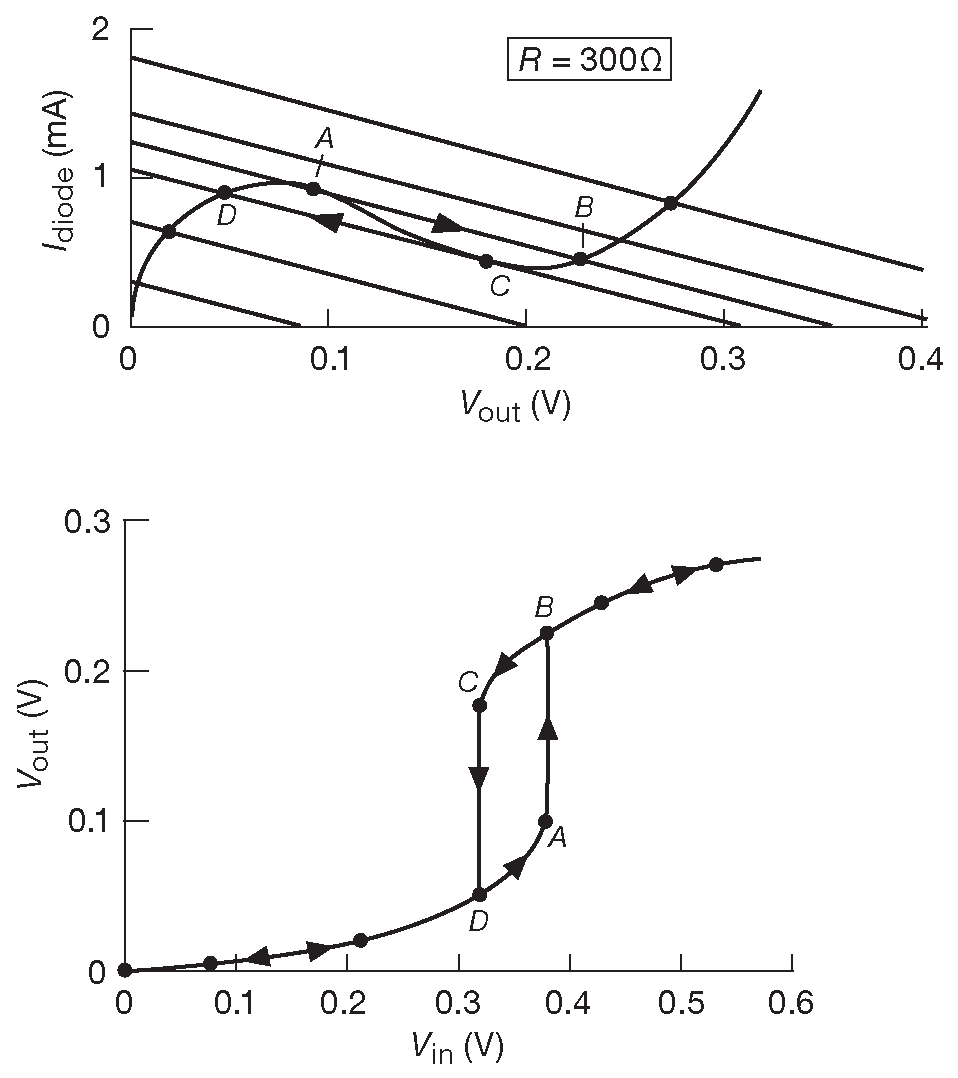
Рис. F.5 Нагрузочные линии и функция передачи для туннельного диода
Рис. F.6 Наличие области \(|R_{load}\space| > |R_{neg}\space|\) порождает гистерезисную переключательную характеристику схем на туннельных диодах
==1114
1 Интересующая точка, известная также как рабочая точка , описывает возможные сочетания постоянного тока и напряжения для схемы, в которой нет сигналов переменного тока. <-

